Until now we worked with alignments between two sequences, but it is likely that you will want to align many sequences at the same time. For example, if you are trying to gain insight on the evolutionary relationships between all of the 16S bacterial genes in a given sample, it would be time consuming and very inefficient to compare them two at a time. It would be more efficient and useful to compare all of the 16S sequences from the bacteria in the same alignment. In the pairwise sequence alignment chapter, we went over dynamic programming algorithms. It's possible to generalize Smith-Waterman and Needleman-Wunsch, the dynamic programming algorithms that we explored for pairwise sequence alignment, to identify the optimal alignment of more than two sequences. Remember that our scoring scheme for pairwise alignment with Smith-Waterman looked like the following:
To generalize this to three sequences, we could create $3 \times 3$ scoring, dynamic programming, and traceback matrices. Our scoring scheme would then look like the following:
However the complexity of this algorithm is much worse than for pairwise alignment. For pairwise alignment, remember that if aligning two sequences of lengths $m$ and $n$, the runtime of the algorithm will be proportional to $m \times n$. If $n$ is longer than or as long as $m$, we simplify the statement to say that the runtime of the algorithm will be be proportional to $n^2$. This curve has a pretty scary trajectory: runtime for pairwise alignment with dynamic programming is said to scale quadratically.
%pylab inline
from functools import partial
from IPython.core import page
page.page = print
import matplotlib.pyplot as plt
seq_lengths = range(25)
s2_times = [t ** 2 for t in range(25)]
plt.plot(range(25), s2_times)
plt.xlabel('Sequence Length')
plt.ylabel('Runtime (s)')
The exponent in the $n^2$ term comes from the fact that, in pairwise alignment, if we assume our sequences are both of length $n$, there are $n \times n$ cells to fill in in the dynamic programming matrix. If we were to generalize either Smith-Waterman or Needleman-Wunsch to three sequences, we would need to create a 3 dimensional array to score and trace back the alignment. For sequences of length $n$, we would therefore have $n \times n \times n$ cells to fill in, and our runtime versus sequence length curve would look like the following.
s3_times = [t ** 3 for t in range(25)]
plt.plot(range(25), s3_times)
plt.xlabel('Sequence Length')
plt.ylabel('Runtime (s)')
That curve looks steeper than the curve for pairwise alignment, and the values on the y-axis are bigger, but it's not really clear how much of a problem this is until we plot runtime for three sequences in the context of the run times for pairwise alignment.
plt.plot(range(25), s2_times)
plt.plot(range(25), s3_times)
plt.xlabel('Sequence Length')
plt.ylabel('Runtime (s)')
And for four sequences:
s4_times = [t ** 4 for t in range(25)]
plt.plot(range(25), s2_times)
plt.plot(range(25), s3_times)
plt.plot(range(25), s4_times)
plt.xlabel('Sequence Length')
plt.ylabel('Runtime (s)')
We clearly have a problem here, and that is that the runtime for multiple sequence alignment using full dynamic programming algorithms grows exponentially with the number of sequences to be aligned. If $n$ is our sequence length, and $s$ is the number of sequences, that means that runtime is proportional to $n^s$. In pairwise alignment, $s$ is always equal to 2, so the problem is more manageable. However, for the general case of $s$ sequences, we really can't even consider Smith-Waterman or Needleman-Wunsch for more than just a few sequences. The pattern in the plots above should illustrate why.
As we explored with database searching, we need to figure out how to align fewer sequences. This is where progressive alignment comes in.
In progressive alignment, the problem of exponential growth of runtime and space is managed by selectively aligning pairs of sequences, and aligning alignments of sequences. What we typically do is identify a pair of closely related sequences, and align those. Then, we identify the next most closely related sequence to that initial pair, and align that sequence to the alignment. This concept of aligning a sequence to an alignment is new, and we'll come back to it in just a few minutes. The other concept of identifying the most closely related sequences, and then the next most closely related sequence, and so on should sound familiar. It effectively means that we're traversing a tree. And herein lies our problem: we need a tree to efficiently align multiple sequences, but we need an alignment to build a good tree.
You probably have two burning questions in your mind right now:
- How do we build a tree to guide the alignment process, if we need an alignment to build a good tree?
- How do we align a sequence to an alignment, or an alignment to an alignment?
We'll explore both of those through-out the rest of this notebook. First, let's cover the process of progressive multiple sequence alignment, just assuming for a moment that we know how to do both of those things.
The process of progressive multiple sequence alignment could look like the following. First, we start with some sequences and a tree representing the relationship between those sequences. We'll call this our guide tree, because it's going to guide us through the process of multiple sequence alignment. In progressive multiple sequence alignment, we build a multiple sequence alignment for each internal node of the tree, where the alignment at a given internal node contains all of the sequences in the clade defined by that node.
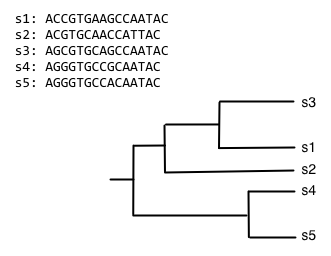
Starting from the root node, descend the bottom branch of the tree until you get to the an internal node. If an alignment hasn't been constructed for that node yet, continue descending the tree until to get to a pair of nodes. In this case, we follow the two branches to the tips. We then align the sequences at that pair of tips (usually with Needleman-Wunsch, for multiple sequence alignment), and assign that alignment to the node connecting those tips.
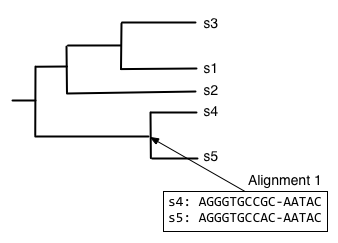
Next, we want to find what to align the resulting alignment to, so start from the root node and descend the top branch of the tree. When you get to the next node, determine if an alignment has already been created for that node. If not, our job is to build that alignment so we have something to align against. In this case, that means that we need to align s1, s2, and s3. We can achieve this by aligning s1 and s3 first, to get the alignment at the internal node connecting them.
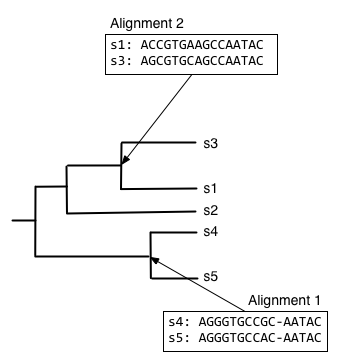
We can next align the alignment of s1 and s3 with s2, to get the alignment at the internal node connecting those clades.
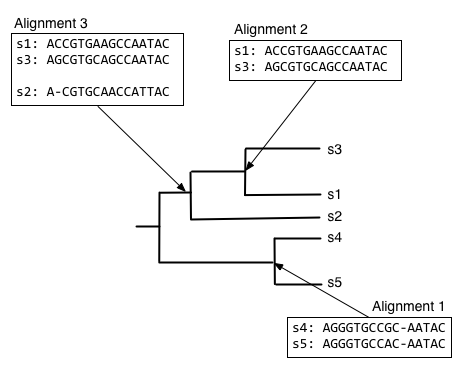
And finally, we can compute the alignment at the root node of the tree, by aligning the alignment of s1, s2, and s3 with the alignment of s4 and s5.
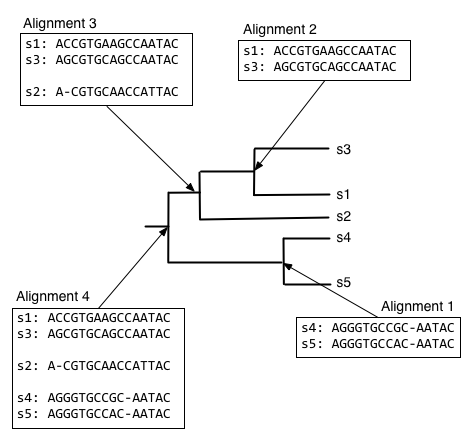
The alignment at the root node is our multiple sequence alignment.
Let's address the first of our outstanding questions. I mentioned above that we need an alignment to build a good tree. The key word here is good. We can build a very rough tree - one that we would never want to present as representing the actual relationships between the sequences in question - without first aligning the sequences. Remember that building a UPGMA tree requires only a distance matrix, so if we can find a non-alignment-dependent way to compute distances between the sequences, we can build a rough UPGMA tree from them.
Let's compute distances between the sequences based on their word composition. We'll define a word here as k adjacent characters in the sequence. We can then define a function that will return all of the words in a sequence as follows. These words can be defined as being overlapping, or non-overlapping. We'll go with overlapping for this example, as the more words we have, the better our guide tree should be.
from skbio import DNA
%psource DNA.iter_kmers
for e in DNA("ACCGGTGACCAGTTGACCAGTA").iter_kmers(3):
print(e)
for e in DNA("ACCGGTGACCAGTTGACCAGTA").iter_kmers(7):
print(e)
for e in DNA("ACCGGTGACCAGTTGACCAGTA").iter_kmers(3, overlap=False):
print(e)
If we then have two sequences, we can compute the word counts for each and define a distance between the sequences as the fraction of words that are unique to either sequence.
from iab.algorithms import kmer_distance
%psource kmer_distance
We can then use this as a distance function...
s1 = DNA("ACCGGTGACCAGTTGACCAGT")
s2 = DNA("ATCGGTACCGGTAGAAGT")
s3 = DNA("GGTACCAAATAGAA")
print(s1.distance(s2, kmer_distance))
print(s1.distance(s3, kmer_distance))
If we wanted to override the default to create (for example) a 5-mer distance function, we could use functools.partial.
fivemer_distance = partial(kmer_distance, k=5)
s1 = DNA("ACCGGTGACCAGTTGACCAGT")
s2 = DNA("ATCGGTACCGGTAGAAGT")
s3 = DNA("GGTACCAAATAGAA")
print(s1.distance(s2, fivemer_distance))
print(s1.distance(s3, fivemer_distance))
We can now apply one of these functions to build a distance matrix for a set of sequences that we want to align.
query_sequences = [DNA("ACCGGTGACCAGTTGACCAGT", {"id": "s1"}),
DNA("ATCGGTACCGGTAGAAGT", {"id": "s2"}),
DNA("GGTACCAAATAGAA", {"id": "s3"}),
DNA("GGCACCAAACAGAA", {"id": "s4"}),
DNA("GGCCCACTGAT", {"id": "s5"})]
from skbio import DistanceMatrix
guide_dm = DistanceMatrix.from_iterable(query_sequences, metric=kmer_distance, key='id')
scikit-bio also has some basic visualization functionality for these objects. For example, we can easily visualize this object as a heatmap.
fig = guide_dm.plot(cmap='Greens')
We can next use some functionality from SciPy to cluster the sequences with UPGMA, and print out a dendrogram.
from scipy.cluster.hierarchy import average, dendrogram, to_tree
for q in query_sequences:
print(q)
guide_lm = average(guide_dm.condensed_form())
guide_d = dendrogram(guide_lm, labels=guide_dm.ids, orientation='right',
link_color_func=lambda x: 'black')
guide_tree = to_tree(guide_lm)
from iab.algorithms import guide_tree_from_sequences
%psource guide_tree_from_sequences
t = guide_tree_from_sequences(query_sequences, display_tree=True)
We now have a guide tree, so we can move on to the next step of progressive alignment.
Next, we'll address our second burning question: aligning alignments. As illustrated above, there are basically three different types of pairwise alignment we need to support for progressive multiple sequence alignment with Needleman-Wunsch. These are:
- Alignment of a pair of sequences.
- Alignment of a sequence and an alignment.
- Alignment of a pair of alignments.
Standard Needleman-Wunsch supports the first, and it is very easy to generalize it to support the latter two. The only change that is necessary is in how the alignment of two non-gap characters is scored. Recall that we previously scored an alignment of two characters by looking up the score of substitution from one to the other in a substitution matrix. To adapt this for aligning a sequence to an alignment, or for aligning an alignment to an alignment, we compute this substitution as the average score of aligning the pairs of characters.
For example, if we want to align the alignment column from $aln1$:
A
C
to the alignment column from $aln2$:
T
G
we could compute the substitution score using the matrix $m$ as:
The following code adapts our implementation of Needleman-Wunsch to support aligning a sequence to an alignment, or aligning an alignment to an alignment.
from iab.algorithms import format_dynamic_programming_matrix, format_traceback_matrix
from skbio.alignment._pairwise import _compute_score_and_traceback_matrices
%psource _compute_score_and_traceback_matrices
from skbio.alignment._pairwise import _traceback
%psource _traceback
from skbio.alignment import global_pairwise_align_nucleotide
%psource global_pairwise_align_nucleotide
For the sake of the examples below, I'm going to override one of the global_pairwise_align_nucleotide defaults to penalize terminal gaps. This effectively tells the algorithm that we know we have a collection of sequences that are homologous from beginning to end.
global_pairwise_align_nucleotide = partial(global_pairwise_align_nucleotide, penalize_terminal_gaps=True)
For example, we can still use this code to align pairs of sequences (but note that we now need to pass those sequences in as a pair of one-item lists):
aln1, _, _ = global_pairwise_align_nucleotide(query_sequences[0], query_sequences[1])
print(aln1)
We can align that alignment to one of our other sequences.
aln1, _, _ = global_pairwise_align_nucleotide(aln1, query_sequences[2])
print(aln1)
Alternatively, we can align another pair of sequences:
aln2, _, _ = global_pairwise_align_nucleotide(query_sequences[2], query_sequences[3])
print(aln2)
And then align that alignment against our previous alignment:
aln3, _, _ = global_pairwise_align_nucleotide(aln1, aln2)
print(aln3)
We can now combine all of these steps to take a set of query sequences, build a guide tree, perform progressive multiple sequence alignment, and return the guide tree (as a SciPy linkage matrix) and the alignment.
from skbio import TreeNode
guide_tree = TreeNode.from_linkage_matrix(guide_lm, guide_dm.ids)
We can view the guide tree in Newick format as follows:
print(guide_tree)
from iab.algorithms import progressive_msa
%psource progressive_msa
msa = progressive_msa(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, guide_tree=guide_tree)
print(msa)
We can now build a (hopefully) improved tree from our multiple sequence alignment. First we'll look at our original distance matrix again, and then the distance matrix generated from the progressive multiple sequence alignment.
fig = guide_dm.plot(cmap='Greens')
msa_dm = DistanceMatrix.from_iterable(msa, metric=kmer_distance)
fig = msa_dm.plot(cmap='Greens')
The UPGMA trees that result from these alignments are very different. First we'll look at the guide tree, and then the tree resulting from the progressive multiple sequence alignment.
d = dendrogram(guide_lm, labels=guide_dm.ids, orientation='right',
link_color_func=lambda x: 'black')
msa_lm = average(msa_dm.condensed_form())
d = dendrogram(msa_lm, labels=msa_dm.ids, orientation='right',
link_color_func=lambda x: 'black')
And we can wrap this all up in a single convenience function:
from iab.algorithms import progressive_msa_and_tree
%psource progressive_msa_and_tree
msa = progressive_msa(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, guide_tree=guide_tree)
msa, tree = progressive_msa_and_tree(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide,
display_tree=True, display_aln=True)
In an iterative alignment, the output tree from the above progressive alignment is used as a guide tree, and the full process repeated. This is performed to reduce errors that result from a low-quality guide tree.
from iab.algorithms import iterative_msa_and_tree
%psource iterative_msa_and_tree
msa, tree = iterative_msa_and_tree(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, num_iterations=1, display_aln=True, display_tree=True)
msa, tree = iterative_msa_and_tree(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, num_iterations=2, display_aln=True, display_tree=True)
msa, tree = iterative_msa_and_tree(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, num_iterations=3, display_aln=True, display_tree=True)
msa, tree = iterative_msa_and_tree(query_sequences, pairwise_aligner=global_pairwise_align_nucleotide, num_iterations=5, display_aln=True, display_tree=True)