07 - Ensemble Methods¶
by Alejandro Correa Bahnsen & Iván Torroledo
version 1.3, June 2018
Part of the class Applied Deep Learning¶
This notebook is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. Special thanks goes to Kevin Markham
Why are we learning about ensembling?
- Very popular method for improving the predictive performance of machine learning models
- Provides a foundation for understanding more sophisticated models
Lesson objectives¶
Students will be able to:
- Define ensembling and its requirements
- Identify the two basic methods of ensembling
- Decide whether manual ensembling is a useful approach for a given problem
- Explain bagging and how it can be applied to decision trees
- Explain how out-of-bag error and feature importances are calculated from bagged trees
- Explain the difference between bagged trees and Random Forests
- Build and tune a Random Forest model in scikit-learn
- Decide whether a decision tree or a Random Forest is a better model for a given problem
Part 1: Introduction¶
Ensemble learning is a widely studied topic in the machine learning community. The main idea behind the ensemble methodology is to combine several individual base classifiers in order to have a classifier that outperforms each of them.
Nowadays, ensemble methods are one of the most popular and well studied machine learning techniques, and it can be noted that since 2009 all the first-place and second-place winners of the KDD-Cup https://www.sigkdd.org/kddcup/ used ensemble methods. The core principle in ensemble learning, is to induce random perturbations into the learning procedure in order to produce several different base classifiers from a single training set, then combining the base classifiers in order to make the final prediction. In order to induce the random permutations and therefore create the different base classifiers, several methods have been proposed, in particular:
- bagging
- pasting
- random forests
- random patches
Finally, after the base classifiers are trained, they are typically combined using either:
- majority voting
- weighted voting
- stacking
There are three main reasons regarding why ensemble methods perform better than single models: statistical, computational and representational . First, from a statistical point of view, when the learning set is too small, an algorithm can find several good models within the search space, that arise to the same performance on the training set $\mathcal{S}$. Nevertheless, without a validation set, there is a risk of choosing the wrong model. The second reason is computational; in general, algorithms rely on some local search optimization and may get stuck in a local optima. Then, an ensemble may solve this by focusing different algorithms to different spaces across the training set. The last reason is representational. In most cases, for a learning set of finite size, the true function $f$ cannot be represented by any of the candidate models. By combining several models in an ensemble, it may be possible to obtain a model with a larger coverage across the space of representable functions.
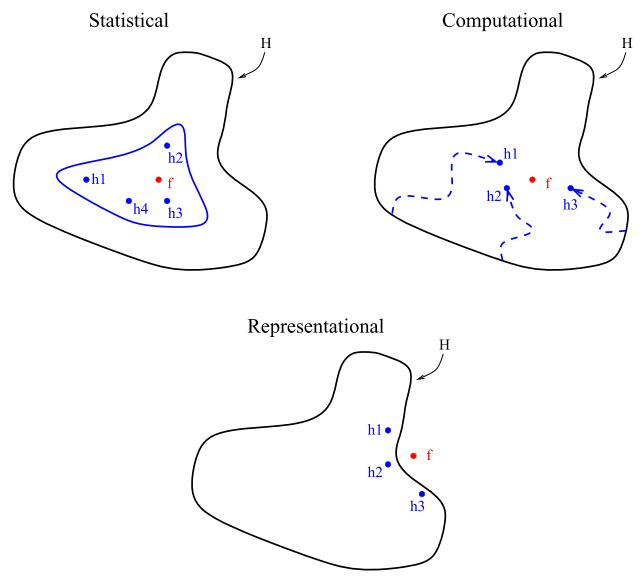
Example¶
Let's pretend that instead of building a single model to solve a binary classification problem, you created five independent models, and each model was correct about 70% of the time. If you combined these models into an "ensemble" and used their majority vote as a prediction, how often would the ensemble be correct?
import numpy as np
# set a seed for reproducibility
np.random.seed(1234)
# generate 1000 random numbers (between 0 and 1) for each model, representing 1000 observations
mod1 = np.random.rand(1000)
mod2 = np.random.rand(1000)
mod3 = np.random.rand(1000)
mod4 = np.random.rand(1000)
mod5 = np.random.rand(1000)
# each model independently predicts 1 (the "correct response") if random number was at least 0.3
preds1 = np.where(mod1 > 0.3, 1, 0)
preds2 = np.where(mod2 > 0.3, 1, 0)
preds3 = np.where(mod3 > 0.3, 1, 0)
preds4 = np.where(mod4 > 0.3, 1, 0)
preds5 = np.where(mod5 > 0.3, 1, 0)
# print the first 20 predictions from each model
print(preds1[:20])
print(preds2[:20])
print(preds3[:20])
print(preds4[:20])
print(preds5[:20])
[0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 0 1 1] [1 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 1 0 0 0] [1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 1 1] [1 1 0 0 0 0 1 1 0 1 1 1 1 1 1 0 1 1 1 0] [0 0 1 0 0 0 1 0 1 0 0 0 1 1 1 1 1 1 1 1]
# average the predictions and then round to 0 or 1
ensemble_preds = np.round((preds1 + preds2 + preds3 + preds4 + preds5)/5.0).astype(int)
# print the ensemble's first 20 predictions
print(ensemble_preds[:20])
[1 1 1 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 1 1]
# how accurate was each individual model?
print(preds1.mean())
print(preds2.mean())
print(preds3.mean())
print(preds4.mean())
print(preds5.mean())
0.713 0.665 0.717 0.712 0.687
# how accurate was the ensemble?
print(ensemble_preds.mean())
0.841
Note: As you add more models to the voting process, the probability of error decreases, which is known as Condorcet's Jury Theorem.
What is ensembling?¶
Ensemble learning (or "ensembling") is the process of combining several predictive models in order to produce a combined model that is more accurate than any individual model.
- Regression: take the average of the predictions
- Classification: take a vote and use the most common prediction, or take the average of the predicted probabilities
For ensembling to work well, the models must have the following characteristics:
- Accurate: they outperform the null model
- Independent: their predictions are generated using different processes
The big idea: If you have a collection of individually imperfect (and independent) models, the "one-off" mistakes made by each model are probably not going to be made by the rest of the models, and thus the mistakes will be discarded when averaging the models.
There are two basic methods for ensembling:
- Manually ensemble your individual models
- Use a model that ensembles for you
Theoretical performance of an ensemble¶
If we assume that each one of the $T$ base classifiers has a probability $\rho$ of being correct, the probability of an ensemble making the correct decision, assuming independence, denoted by $P_c$, can be calculated using the binomial distribution
$$P_c = \sum_{j>T/2}^{T} {{T}\choose{j}} \rho^j(1-\rho)^{T-j}.$$Furthermore, as shown, if $T\ge3$ then:
$$ \lim_{T \to \infty} P_c= \begin{cases} 1 &\mbox{if } \rho>0.5 \\ 0 &\mbox{if } \rho<0.5 \\ 0.5 &\mbox{if } \rho=0.5 , \end{cases} $$leading to the conclusion that
Part 2: Manual ensembling¶
What makes a good manual ensemble?
- Different types of models
- Different combinations of features
- Different tuning parameters
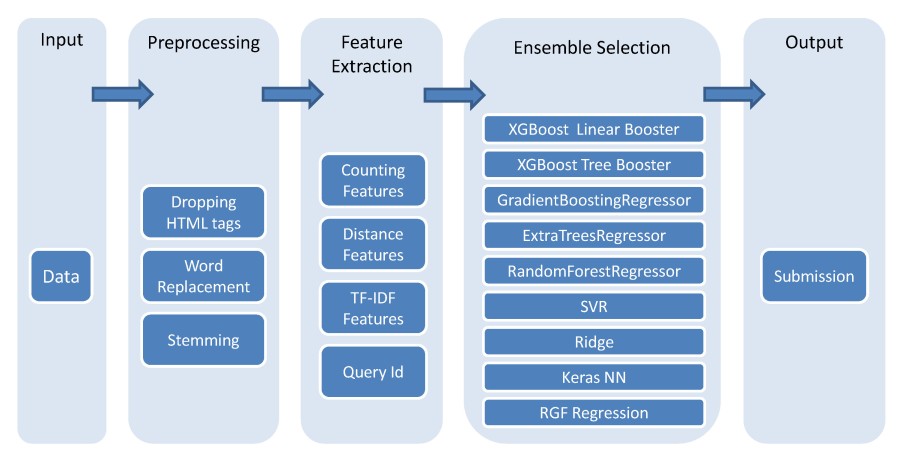
Machine learning flowchart created by the winner of Kaggle's CrowdFlower competition
# read in and prepare the vehicle training data
import zipfile
import pandas as pd
with zipfile.ZipFile('../datasets/vehicles_train.csv.zip', 'r') as z:
f = z.open('vehicles_train.csv')
train = pd.io.parsers.read_table(f, index_col=False, sep=',')
with zipfile.ZipFile('../datasets/vehicles_test.csv.zip', 'r') as z:
f = z.open('vehicles_test.csv')
test = pd.io.parsers.read_table(f, index_col=False, sep=',')
train['vtype'] = train.vtype.map({'car':0, 'truck':1})
# read in and prepare the vehicle testing data
test['vtype'] = test.vtype.map({'car':0, 'truck':1})
train.head()
| price | year | miles | doors | vtype | |
|---|---|---|---|---|---|
| 0 | 22000 | 2012 | 13000 | 2 | 0 |
| 1 | 14000 | 2010 | 30000 | 2 | 0 |
| 2 | 13000 | 2010 | 73500 | 4 | 0 |
| 3 | 9500 | 2009 | 78000 | 4 | 0 |
| 4 | 9000 | 2007 | 47000 | 4 | 0 |
Train different models¶
from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsRegressor
models = {'lr': LinearRegression(),
'dt': DecisionTreeRegressor(),
'nb': GaussianNB(),
'nn': KNeighborsRegressor()}
# Train all the models
X_train = train.iloc[:, 1:]
X_test = test.iloc[:, 1:]
y_train = train.price
y_test = test.price
for model in models.keys():
models[model].fit(X_train, y_train)
# predict test for each model
y_pred = pd.DataFrame(index=test.index, columns=models.keys())
for model in models.keys():
y_pred[model] = models[model].predict(X_test)
# Evaluate each model
from sklearn.metrics import mean_squared_error
for model in models.keys():
print(model,np.sqrt(mean_squared_error(y_pred[model], y_test)))
lr 2138.3579028745116 dt 1414.213562373095 nb 5477.2255750516615 nn 1671.3268182295567
Evaluate the error of the mean of the predictions¶
np.sqrt(mean_squared_error(y_pred.mean(axis=1), y_test))
1193.164765760328
Comparing manual ensembling with a single model approach¶
Advantages of manual ensembling:
- Increases predictive accuracy
- Easy to get started
Disadvantages of manual ensembling:
- Decreases interpretability
- Takes longer to train
- Takes longer to predict
- More complex to automate and maintain
- Small gains in accuracy may not be worth the added complexity
Part 3: Bagging¶
The primary weakness of decision trees is that they don't tend to have the best predictive accuracy. This is partially due to high variance, meaning that different splits in the training data can lead to very different trees.
Bagging is a general purpose procedure for reducing the variance of a machine learning method, but is particularly useful for decision trees. Bagging is short for bootstrap aggregation, meaning the aggregation of bootstrap samples.
What is a bootstrap sample? A random sample with replacement:
# set a seed for reproducibility
np.random.seed(1)
# create an array of 1 through 20
nums = np.arange(1, 21)
print(nums)
# sample that array 20 times with replacement
print(np.random.choice(a=nums, size=20, replace=True))
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20] [ 6 12 13 9 10 12 6 16 1 17 2 13 8 14 7 19 6 19 12 11]
How does bagging work (for decision trees)?
- Grow B trees using B bootstrap samples from the training data.
- Train each tree on its bootstrap sample and make predictions.
- Combine the predictions:
- Average the predictions for regression trees
- Take a vote for classification trees
Notes:
- Each bootstrap sample should be the same size as the original training set.
- B should be a large enough value that the error seems to have "stabilized".
- The trees are grown deep so that they have low bias/high variance.
Bagging increases predictive accuracy by reducing the variance, similar to how cross-validation reduces the variance associated with train/test split (for estimating out-of-sample error) by splitting many times an averaging the results.
# set a seed for reproducibility
np.random.seed(123)
n_samples = train.shape[0]
n_B = 10
# create ten bootstrap samples (will be used to select rows from the DataFrame)
samples = [np.random.choice(a=n_samples, size=n_samples, replace=True) for _ in range(1, n_B +1 )]
samples
[array([13, 2, 12, 2, 6, 1, 3, 10, 11, 9, 6, 1, 0, 1]), array([ 9, 0, 0, 9, 3, 13, 4, 0, 0, 4, 1, 7, 3, 2]), array([ 4, 7, 2, 4, 8, 13, 0, 7, 9, 3, 12, 12, 4, 6]), array([ 1, 5, 6, 11, 2, 1, 12, 8, 3, 10, 5, 0, 11, 2]), array([10, 10, 6, 13, 2, 4, 11, 11, 13, 12, 4, 6, 13, 3]), array([10, 0, 6, 4, 7, 11, 6, 7, 1, 11, 10, 5, 7, 9]), array([ 2, 4, 8, 1, 12, 2, 1, 1, 3, 12, 5, 9, 0, 8]), array([11, 1, 6, 3, 3, 11, 5, 9, 7, 9, 2, 3, 11, 3]), array([ 3, 8, 6, 9, 7, 6, 3, 9, 6, 12, 6, 11, 6, 1]), array([13, 10, 3, 4, 3, 1, 13, 0, 5, 8, 13, 6, 11, 8])]
# show the rows for the first decision tree
train.iloc[samples[0], :]
| price | year | miles | doors | vtype | |
|---|---|---|---|---|---|
| 13 | 1300 | 1997 | 138000 | 4 | 0 |
| 2 | 13000 | 2010 | 73500 | 4 | 0 |
| 12 | 1800 | 1999 | 163000 | 2 | 1 |
| 2 | 13000 | 2010 | 73500 | 4 | 0 |
| 6 | 3000 | 2004 | 177000 | 4 | 0 |
| 1 | 14000 | 2010 | 30000 | 2 | 0 |
| 3 | 9500 | 2009 | 78000 | 4 | 0 |
| 10 | 2500 | 2003 | 190000 | 2 | 1 |
| 11 | 5000 | 2001 | 62000 | 4 | 0 |
| 9 | 1900 | 2003 | 160000 | 4 | 0 |
| 6 | 3000 | 2004 | 177000 | 4 | 0 |
| 1 | 14000 | 2010 | 30000 | 2 | 0 |
| 0 | 22000 | 2012 | 13000 | 2 | 0 |
| 1 | 14000 | 2010 | 30000 | 2 | 0 |
Build one tree for each sample
from sklearn.tree import DecisionTreeRegressor
# grow each tree deep
treereg = DecisionTreeRegressor(max_depth=None, random_state=123)
# DataFrame for storing predicted price from each tree
y_pred = pd.DataFrame(index=test.index, columns=[list(range(n_B))])
# grow one tree for each bootstrap sample and make predictions on testing data
for i, sample in enumerate(samples):
X_train = train.iloc[sample, 1:]
y_train = train.iloc[sample, 0]
treereg.fit(X_train, y_train)
y_pred[i] = treereg.predict(X_test)
y_pred
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1300.0 | 1300.0 | 3000.0 | 4000.0 | 1300.0 | 4000.0 | 4000.0 | 4000.0 | 3000.0 | 4000.0 |
| 1 | 5000.0 | 1300.0 | 3000.0 | 5000.0 | 5000.0 | 5000.0 | 4000.0 | 5000.0 | 5000.0 | 5000.0 |
| 2 | 14000.0 | 13000.0 | 13000.0 | 13000.0 | 13000.0 | 14000.0 | 13000.0 | 13000.0 | 9500.0 | 9000.0 |
Results of each tree
for i in range(n_B):
print(i, np.sqrt(mean_squared_error(y_pred[i], y_test)))
0 1621.7274740226856 1 2942.7877939124323 2 1825.7418583505537 3 1000.0 4 1276.7145334803704 5 1414.213562373095 6 1414.213562373095 7 1000.0 8 1554.5631755148024 9 1914.854215512676
Results of the ensemble
y_pred.mean(axis=1)
0 2990.0 1 4330.0 2 12450.0 dtype: float64
np.sqrt(mean_squared_error(y_test, y_pred.mean(axis=1)))
998.5823284370031
Bagged decision trees in scikit-learn (with B=500)¶
# define the training and testing sets
X_train = train.iloc[:, 1:]
y_train = train.iloc[:, 0]
X_test = test.iloc[:, 1:]
y_test = test.iloc[:, 0]
# instruct BaggingRegressor to use DecisionTreeRegressor as the "base estimator"
from sklearn.ensemble import BaggingRegressor
bagreg = BaggingRegressor(DecisionTreeRegressor(), n_estimators=500,
bootstrap=True, oob_score=True, random_state=1)
# fit and predict
bagreg.fit(X_train, y_train)
y_pred = bagreg.predict(X_test)
y_pred
array([ 3344.2, 5395. , 12902. ])
# calculate RMSE
np.sqrt(mean_squared_error(y_test, y_pred))
657.8000304043775
Estimating out-of-sample error¶
For bagged models, out-of-sample error can be estimated without using train/test split or cross-validation!
On average, each bagged tree uses about two-thirds of the observations. For each tree, the remaining observations are called "out-of-bag" observations.
# show the first bootstrap sample
samples[0]
array([13, 2, 12, 2, 6, 1, 3, 10, 11, 9, 6, 1, 0, 1])
# show the "in-bag" observations for each sample
for sample in samples:
print(set(sample))
{0, 1, 2, 3, 6, 9, 10, 11, 12, 13}
{0, 1, 2, 3, 4, 7, 9, 13}
{0, 2, 3, 4, 6, 7, 8, 9, 12, 13}
{0, 1, 2, 3, 5, 6, 8, 10, 11, 12}
{2, 3, 4, 6, 10, 11, 12, 13}
{0, 1, 4, 5, 6, 7, 9, 10, 11}
{0, 1, 2, 3, 4, 5, 8, 9, 12}
{1, 2, 3, 5, 6, 7, 9, 11}
{1, 3, 6, 7, 8, 9, 11, 12}
{0, 1, 3, 4, 5, 6, 8, 10, 11, 13}
# show the "out-of-bag" observations for each sample
for sample in samples:
print(sorted(set(range(n_samples)) - set(sample)))
[4, 5, 7, 8] [5, 6, 8, 10, 11, 12] [1, 5, 10, 11] [4, 7, 9, 13] [0, 1, 5, 7, 8, 9] [2, 3, 8, 12, 13] [6, 7, 10, 11, 13] [0, 4, 8, 10, 12, 13] [0, 2, 4, 5, 10, 13] [2, 7, 9, 12]
How to calculate "out-of-bag error":
- For every observation in the training data, predict its response value using only the trees in which that observation was out-of-bag. Average those predictions (for regression) or take a vote (for classification).
- Compare all predictions to the actual response values in order to compute the out-of-bag error.
When B is sufficiently large, the out-of-bag error is an accurate estimate of out-of-sample error.
# compute the out-of-bag R-squared score (not MSE, unfortunately!) for B=500
bagreg.oob_score_
0.7986955133989982
Estimating feature importance¶
Bagging increases predictive accuracy, but decreases model interpretability because it's no longer possible to visualize the tree to understand the importance of each feature.
However, we can still obtain an overall summary of feature importance from bagged models:
- Bagged regression trees: calculate the total amount that MSE is decreased due to splits over a given feature, averaged over all trees
- Bagged classification trees: calculate the total amount that Gini index is decreased due to splits over a given feature, averaged over all trees
Part 4: Random Forests¶
Random Forests is a slight variation of bagged trees that has even better performance:
- Exactly like bagging, we create an ensemble of decision trees using bootstrapped samples of the training set.
- However, when building each tree, each time a split is considered, a random sample of m features is chosen as split candidates from the full set of p features. The split is only allowed to use one of those m features.
- A new random sample of features is chosen for every single tree at every single split.
- For classification, m is typically chosen to be the square root of p.
- For regression, m is typically chosen to be somewhere between p/3 and p.
What's the point?
- Suppose there is one very strong feature in the data set. When using bagged trees, most of the trees will use that feature as the top split, resulting in an ensemble of similar trees that are highly correlated.
- Averaging highly correlated quantities does not significantly reduce variance (which is the entire goal of bagging).
- By randomly leaving out candidate features from each split, Random Forests "decorrelates" the trees, such that the averaging process can reduce the variance of the resulting model.
Part 5: Building and tuning decision trees and Random Forests¶
- Major League Baseball player data from 1986-87: data, data dictionary (page 7)
- Each observation represents a player
- Goal: Predict player salary
# read in the data
with zipfile.ZipFile('../datasets/hitters.csv.zip', 'r') as z:
f = z.open('hitters.csv')
hitters = pd.read_csv(f, sep=',', index_col=False)
# remove rows with missing values
hitters.dropna(inplace=True)
hitters.head()
| AtBat | Hits | HmRun | Runs | RBI | Walks | Years | CAtBat | CHits | CHmRun | CRuns | CRBI | CWalks | League | Division | PutOuts | Assists | Errors | Salary | NewLeague | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 315 | 81 | 7 | 24 | 38 | 39 | 14 | 3449 | 835 | 69 | 321 | 414 | 375 | N | W | 632 | 43 | 10 | 475.0 | N |
| 2 | 479 | 130 | 18 | 66 | 72 | 76 | 3 | 1624 | 457 | 63 | 224 | 266 | 263 | A | W | 880 | 82 | 14 | 480.0 | A |
| 3 | 496 | 141 | 20 | 65 | 78 | 37 | 11 | 5628 | 1575 | 225 | 828 | 838 | 354 | N | E | 200 | 11 | 3 | 500.0 | N |
| 4 | 321 | 87 | 10 | 39 | 42 | 30 | 2 | 396 | 101 | 12 | 48 | 46 | 33 | N | E | 805 | 40 | 4 | 91.5 | N |
| 5 | 594 | 169 | 4 | 74 | 51 | 35 | 11 | 4408 | 1133 | 19 | 501 | 336 | 194 | A | W | 282 | 421 | 25 | 750.0 | A |
# encode categorical variables as integers
hitters['League'] = pd.factorize(hitters.League)[0]
hitters['Division'] = pd.factorize(hitters.Division)[0]
hitters['NewLeague'] = pd.factorize(hitters.NewLeague)[0]
hitters.head()
| AtBat | Hits | HmRun | Runs | RBI | Walks | Years | CAtBat | CHits | CHmRun | CRuns | CRBI | CWalks | League | Division | PutOuts | Assists | Errors | Salary | NewLeague | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 315 | 81 | 7 | 24 | 38 | 39 | 14 | 3449 | 835 | 69 | 321 | 414 | 375 | 0 | 0 | 632 | 43 | 10 | 475.0 | 0 |
| 2 | 479 | 130 | 18 | 66 | 72 | 76 | 3 | 1624 | 457 | 63 | 224 | 266 | 263 | 1 | 0 | 880 | 82 | 14 | 480.0 | 1 |
| 3 | 496 | 141 | 20 | 65 | 78 | 37 | 11 | 5628 | 1575 | 225 | 828 | 838 | 354 | 0 | 1 | 200 | 11 | 3 | 500.0 | 0 |
| 4 | 321 | 87 | 10 | 39 | 42 | 30 | 2 | 396 | 101 | 12 | 48 | 46 | 33 | 0 | 1 | 805 | 40 | 4 | 91.5 | 0 |
| 5 | 594 | 169 | 4 | 74 | 51 | 35 | 11 | 4408 | 1133 | 19 | 501 | 336 | 194 | 1 | 0 | 282 | 421 | 25 | 750.0 | 1 |
# allow plots to appear in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# scatter plot of Years versus Hits colored by Salary
hitters.plot(kind='scatter', x='Years', y='Hits', c='Salary', colormap='jet', xlim=(0, 25), ylim=(0, 250))
<matplotlib.axes._subplots.AxesSubplot at 0x7fb342be6160>
# define features: exclude career statistics (which start with "C") and the response (Salary)
feature_cols = hitters.columns[hitters.columns.str.startswith('C') == False].drop('Salary')
feature_cols
Index(['AtBat', 'Hits', 'HmRun', 'Runs', 'RBI', 'Walks', 'Years', 'League',
'Division', 'PutOuts', 'Assists', 'Errors', 'NewLeague'],
dtype='object')
# define X and y
X = hitters[feature_cols]
y = hitters.Salary
Predicting salary with a decision tree¶
Find the best max_depth for a decision tree using cross-validation:
# list of values to try for max_depth
max_depth_range = range(1, 21)
# list to store the average RMSE for each value of max_depth
RMSE_scores = []
# use 10-fold cross-validation with each value of max_depth
from sklearn.model_selection import cross_val_score
for depth in max_depth_range:
treereg = DecisionTreeRegressor(max_depth=depth, random_state=1)
MSE_scores = cross_val_score(treereg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_depth (x-axis) versus RMSE (y-axis)
plt.plot(max_depth_range, RMSE_scores)
plt.xlabel('max_depth')
plt.ylabel('RMSE (lower is better)')
Text(0,0.5,'RMSE (lower is better)')
# show the best RMSE and the corresponding max_depth
sorted(zip(RMSE_scores, max_depth_range))[0]
(340.034168704752, 2)
# max_depth=2 was best, so fit a tree using that parameter
treereg = DecisionTreeRegressor(max_depth=2, random_state=1)
treereg.fit(X, y)
DecisionTreeRegressor(criterion='mse', max_depth=2, max_features=None,
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=1, splitter='best')
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':treereg.feature_importances_}).sort_values('importance')
| feature | importance | |
|---|---|---|
| 0 | AtBat | 0.000000 |
| 2 | HmRun | 0.000000 |
| 3 | Runs | 0.000000 |
| 4 | RBI | 0.000000 |
| 5 | Walks | 0.000000 |
| 7 | League | 0.000000 |
| 8 | Division | 0.000000 |
| 9 | PutOuts | 0.000000 |
| 10 | Assists | 0.000000 |
| 11 | Errors | 0.000000 |
| 12 | NewLeague | 0.000000 |
| 6 | Years | 0.488391 |
| 1 | Hits | 0.511609 |
Predicting salary with a Random Forest¶
from sklearn.ensemble import RandomForestRegressor
rfreg = RandomForestRegressor()
rfreg
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
oob_score=False, random_state=None, verbose=0, warm_start=False)
Tuning n_estimators¶
One important tuning parameter is n_estimators, which is the number of trees that should be grown. It should be a large enough value that the error seems to have "stabilized".
# list of values to try for n_estimators
estimator_range = range(10, 310, 10)
# list to store the average RMSE for each value of n_estimators
RMSE_scores = []
# use 5-fold cross-validation with each value of n_estimators (WARNING: SLOW!)
for estimator in estimator_range:
rfreg = RandomForestRegressor(n_estimators=estimator, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=5, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot n_estimators (x-axis) versus RMSE (y-axis)
plt.plot(estimator_range, RMSE_scores)
plt.xlabel('n_estimators')
plt.ylabel('RMSE (lower is better)')
Text(0,0.5,'RMSE (lower is better)')
Tuning max_features¶
The other important tuning parameter is max_features, which is the number of features that should be considered at each split.
# list of values to try for max_features
feature_range = range(1, len(feature_cols)+1)
# list to store the average RMSE for each value of max_features
RMSE_scores = []
# use 10-fold cross-validation with each value of max_features (WARNING: SLOW!)
for feature in feature_range:
rfreg = RandomForestRegressor(n_estimators=150, max_features=feature, random_state=1, n_jobs=-1)
MSE_scores = cross_val_score(rfreg, X, y, cv=10, scoring='neg_mean_squared_error')
RMSE_scores.append(np.mean(np.sqrt(-MSE_scores)))
# plot max_features (x-axis) versus RMSE (y-axis)
plt.plot(feature_range, RMSE_scores)
plt.xlabel('max_features')
plt.ylabel('RMSE (lower is better)')
Text(0,0.5,'RMSE (lower is better)')
# show the best RMSE and the corresponding max_features
sorted(zip(RMSE_scores, feature_range))[0]
(290.0078511328435, 10)
Fitting a Random Forest with the best parameters¶
# max_features=8 is best and n_estimators=150 is sufficiently large
rfreg = RandomForestRegressor(n_estimators=150, max_features=8, max_depth=3, oob_score=True, random_state=1)
rfreg.fit(X, y)
# compute feature importances
pd.DataFrame({'feature':feature_cols, 'importance':rfreg.feature_importances_}).sort_values('importance')
| feature | importance | |
|---|---|---|
| 7 | League | 0.003603 |
| 12 | NewLeague | 0.004290 |
| 8 | Division | 0.005477 |
| 10 | Assists | 0.023842 |
| 11 | Errors | 0.028618 |
| 2 | HmRun | 0.044607 |
| 9 | PutOuts | 0.060063 |
| 3 | Runs | 0.071800 |
| 0 | AtBat | 0.094592 |
| 4 | RBI | 0.130965 |
| 5 | Walks | 0.139899 |
| 1 | Hits | 0.145264 |
| 6 | Years | 0.246980 |
# compute the out-of-bag R-squared score
rfreg.oob_score_
0.5274187002769267
Reducing X to its most important features¶
# check the shape of X
X.shape
(263, 13)
rfreg
RandomForestRegressor(bootstrap=True, criterion='mse', max_depth=None,
max_features=8, max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=150, n_jobs=1, oob_score=True, random_state=1,
verbose=0, warm_start=False)
# set a threshold for which features to include
from sklearn.feature_selection import SelectFromModel
print(SelectFromModel(rfreg, threshold=0.1, prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X).shape)
print(SelectFromModel(rfreg, threshold='median', prefit=True).transform(X).shape)
(263, 4) (263, 5) (263, 7)
# create a new feature matrix that only includes important features
X_important = SelectFromModel(rfreg, threshold='mean', prefit=True).transform(X)
# check the RMSE for a Random Forest that only includes important features
rfreg = RandomForestRegressor(n_estimators=150, max_features=3, random_state=1)
scores = cross_val_score(rfreg, X_important, y, cv=10, scoring='neg_mean_squared_error')
np.mean(np.sqrt(-scores))
284.35550515135395
Comparing Random Forests with decision trees¶
Advantages of Random Forests:
- Performance is competitive with the best supervised learning methods
- Provides a more reliable estimate of feature importance
- Allows you to estimate out-of-sample error without using train/test split or cross-validation
Disadvantages of Random Forests:
- Less interpretable
- Slower to train
- Slower to predict