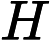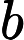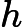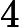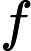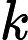1. Motivation¶
___skyTran___ is an elevated transportation infrastructure that utilizes a patented method of passive magnetic levitation (MagLev). Unlike other forms of passive MagLev, the Bogie reacts against vertical conductive surfaces. The Bogie is the driving portion of the vehicle; the passenger-carrying portion hangs below the track and is called the Pod. This design enables the vehicle to control its altitude in software. A strong simulation environment is critical to developing control algorithms without putting hardware at risk.
The objective of this project is to model and simulate the vehicle, and to then determine a favorable maximum levitation height by analyzing the stability of the vehicle system under different maximum-height levitation regimes.

Figure 1: A render of the skyTran MagLev vehicle. Credit: skyTran ¶
2. Background¶
Conventional trains leverage the friction between wheels and rails to drive forward. In contrast, a MagLev vehicle levitates on a guideway, replacing wheels with electromagnets. Levitation is advantageous in numerous ways, such as high speeds, reduction in maintenance costs, reduced noise and vibration levels, quick acceleration and deceleration, and so on. This technology also facilitates emission-free mass transportation.
Though the concept of MagLev trains was introduced in the 1930s, the technology reached maturity only in the 1980s. The first practical public MagLev train service was launched in Shanghai in 2003. Advances in modern technology have enabled full-scale implementation of MagLev trains, which are currently operational in many countries. NASA has investigated the concept of Magnetic Launch Assist, which makes use of both magnetic levitation and magnetic propulsion to propel launch vehicles to 183 meters per second in less than 10 seconds.
skyTran is a novel take on the personal rapid transit (PRT) infrastructure, making use of a network of lightweight Pods that run on elevated guideways, thus facilitating transportation of people and freight from one place to another without the need for intermediate stops.
3. Problem Formulation¶
Figure 2: A CAD-model of the Split-Bogie configuration of the vehicle. Credit: skyTran ¶
3.1 The Vehicle¶
The vehicle system that has been modeled, simulated and analyzed, is the Bogie, which is a cart-like rectangular vehicle with a rotary bearing connecting the front and rear chassis shown in figure 2. It has four wheels, one at each corner of the body, and four magnetic wings, which, at a high-level, function like an airfoil/fixed-wing, with the ability to effect a lift force on the vehicle. The vehicle is propelled using an axial motor belt and is centered using a set of urethane wheels that roll against the reaction plates, which are shown in figure 3.

Figure 3: Principal views of the vehicle. Credit: skyTran ¶
3.2 Dynamics¶
The vehicle is subject to five important classes of force & torque inputs:
3.2.1 Magnetic Wing: Magnetic Lift and Drag Forces¶
The vehicle has four wings, located at the corners of the rectangular Bogie body. A simplified black-box model of the wing as shown in figure 4 will be considered for the purpose of this project.
The forces effected by the wing arise from the interaction of eddy currents that are induced by the motion of the wing, with the conductive track plate (figure 4).

Figure 4: The Magnetic Wing. Credit: skyTran ¶
3.2.2 Wing Actuators: Pitching Moment¶
The wing actuators cause pitching moments between the chassis and the wing.
3.2.3 Wheels: Normal Force¶
The vehicle has four wheels, located beneath the wings. They are active before lift-off; lift-off is achieved when vehicle reaches critical velocity.
3.2.4 Belt: Drive Force¶
The belt pulls the vehicle forward x-direction.
3.2.5 Belt: Centering Force¶
The belt also provides a lateral centering force, keeping the vehicle very near y=0.
4. The Vehicle Model¶
A simplified version of the vehicle has been modeled. The independent rotational degree of freedom between the front and rear chassis has been eliminated in order to speed-up computation. It is assumed that the track, as defined by motor force direction and reaction plates, is straight, and that there is negligible yaw and lateral motion.
The magnetic wings are at a fixed angle for each simulation run. Gravitational, propulsive, frictional and lift forces have been considered. The drag force is assumed to be negligible. The lift force has been modeled as a function of the pitch-angles of the wings, the speed of the mass-center of the vehicle in the axial direction, and the levitation height.

Figure 5: The lift force generated by the magnetic wing. Credit: skyTran ¶
The magnetic lift-force generated by each wing is modeled as follows:
where,
The lift-force
The coefficient of lift
The axial speed of the vehicle
The pitch-angle of the wing
The maximum levitation height
The altitude of the vehicle
The modeled vehicle is shown in figure 6.

Figure 6: The Vehicle Model ¶
5. Modeling¶
5.1 Dependencies¶
import sympy as sm
import sympy.physics.mechanics as me
from pydy.system import System
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
me.init_vprinting()
5.2 Reference Frames¶
Reference frames are attached to the track (inertial) and each of the five rigid bodies. The reference frame of the Bogie is oriented relative to the inertial reference frame and the wings are oriented relative to the Bogie.
N = me.ReferenceFrame('N') # Inertial Reference Frame
bpitch, broll = me.dynamicsymbols('b_pitch, b_roll')
B = N.orientnew('B', 'Body', [-bpitch, broll, 0], 'YXZ')
alpha1, alpha2, alpha3, alpha4 = sm.symbols('alpha_1, alpha_2, alpha_3, alpha_4')
W1 = B.orientnew('W1', 'Axis', [alpha1, -B.y])
W2 = B.orientnew('W2', 'Axis', [alpha2, -B.y])
W3 = B.orientnew('W3', 'Axis', [alpha3, -B.y])
W4 = B.orientnew('W4', 'Axis', [alpha4, -B.y])
5.3 Points¶
The position vectors of the points that are significant in the formulation of Kane's Equations are defined.
O = me.Point('O') # fixed point in the inertial reference frame
O.set_vel(N, 0)
5.3.1 Mass Centers¶
dx, dz = me.dynamicsymbols('d_x, d_z') # coordinates of the mass-center of the vehicle relative to the point fixed in the inertial reference frame
lb, wb, hb = sm.symbols('l_b, w_b, h_b') # length, width and height of the Bogie
lw, ww, hw = sm.symbols('l_w, w_w, h_w') # length, width and height of each Wing
MB = O.locatenew('M_B', dx * N.x + dz * N.z)
MW1 = MB.locatenew('M_W1', (1/6) * lb * B.x - (1/2) * wb * B.y - (1/2) * ww * W1.y)
MW2 = MB.locatenew('M_W2', (1/6) * lb * B.x + (1/2) * wb * B.y + (1/2) * ww * W1.y)
MW3 = MB.locatenew('M_W3', - (1/6) * lb * B.x - (1/2) * wb * B.y - (1/2) * ww * W1.y)
MW4 = MB.locatenew('M_W4', - (1/6) * lb * B.x + (1/2) * wb * B.y + (1/2) * ww * W1.y)
5.3.2 Wheels¶
P1 = MB.locatenew('P_1', (1/2) * lb * B.x - (1/2) * wb * B.y - (1/2) * hb * B.z)
P2 = MB.locatenew('P_2', (1/2) * lb * B.x + (1/2) * wb * B.y - (1/2) * hb * B.z)
P3 = MB.locatenew('P_3', - (1/2) * lb * B.x - (1/2) * wb * B.y - (1/2) * hb * B.z)
P4 = MB.locatenew('P_4', - (1/2) * lb * B.x + (1/2) * wb * B.y - (1/2) * hb * B.z)
5.4 Kinematical Differential Equations¶
The vehicle in the chosen configuration has four independent generalized coordinates: The axial displacement of the mass-center of the vehicle, , the vertical displacement of the mass-center of the vehicle, , the pitch-angle of the Bogie, , and the roll-angle of the Bogie, . The generalized speeds are chosen to be the time-derivatives of the independent generalized coordinates. The system is holonomic.
u_dx = me.dynamicsymbols('u_d_x')
u_dz = me.dynamicsymbols('u_d_z')
u_bpitch = me.dynamicsymbols('u_b__pitch')
u_broll = me.dynamicsymbols('u_b__roll')
z1 = sm.Eq(u_dx, dx.diff())
z2 = sm.Eq(u_dz, dz.diff())
z3 = sm.Eq(u_bpitch, bpitch.diff())
z4 = sm.Eq(u_broll, broll.diff())
u = sm.solve([z1, z2, z3, z4], dx.diff(), dz.diff(), bpitch.diff(), broll.diff())
u
5.5 Velocities¶
The linear velocities of the significant points are defined. The generalized speeds are substituted in place of the derivatives of the independent generalized coordinates, and the resulting expressions are functions of the independent generalized coordinates and the generalized speeds only.
5.5.1 Velocities of the mass centers¶
MB.set_vel(N, MB.pos_from(O).dt(N))
N_v_MB = MB.vel(N).subs(u)
N_v_MB
N_v_MW1 = MW1.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_MW1
N_v_MW2 = MW2.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_MW2
N_v_MW3 = MW3.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_MW3
N_v_MW4 = MW4.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_MW4
5.5.2 Velocities of the wheels¶
N_v_P1 = P1.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_P1
N_v_P2 = P2.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_P2
N_v_P3 = P3.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_P3
N_v_P4 = P4.v2pt_theory(MB, N, B).subs(u).simplify()
N_v_P4
5.6 Angular Velocities¶
The expressions for the angular velocities of the rigid bodies are made independent of the time-derivatives of the independent generalized coordinates by substituting the corresponding generalized speeds in their places.
B.set_ang_vel(N, B.ang_vel_in(N).subs(u))
B.ang_vel_in(N)
W1.set_ang_vel(N, W1.ang_vel_in(N).subs(u))
W1.ang_vel_in(N)
W2.set_ang_vel(N, W2.ang_vel_in(N).subs(u))
W2.ang_vel_in(N)
W3.set_ang_vel(N, W3.ang_vel_in(N).subs(u))
W3.ang_vel_in(N)
W4.set_ang_vel(N, W4.ang_vel_in(N).subs(u))
W4.ang_vel_in(N)
5.7 Inertia Dyadics¶
The inertia dyadics of the rigid bodies are computed.
mB, mW = sm.symbols('m_B, m_W')
IBx, IBy, IBz, IWx, IWy, IWz = sm.symbols('I_B_x, I_B_y, I_B_z, I_W_x, I_W_y, I_W_z')
IB = me.inertia(B, IBx, IBy, IBz)
IB
IW1 = me.inertia(W1, IWx, IWy, IWz)
IW1
IW2 = me.inertia(W2, IWx, IWy, IWz)
IW2
IW3 = me.inertia(W3, IWx, IWy, IWz)
IW3
IW4 = me.inertia(W4, IWx, IWy, IWz)
IW4
5.8 Loads¶
The loads (forces) acting on the vehicle are defined: gravitational, lift, propulsive, collision (contact/penetration) and frictional forces are considered.
5.8.1 Gravitational Forces¶
g = sm.symbols('g')
G_B = -(mB * g) * N.z
G_W1 = -(mW * g) * N.z
G_W2 = -(mW * g) * N.z
G_W3 = -(mW * g) * N.z
G_W4 = -(mW * g) * N.z
5.8.2 Lift Forces¶
CL, H = sm.symbols('C_L, H')
FL1 = CL * sm.sin(alpha1) * N_v_MB.dot(N.x).subs(u) * (H - dz) * N.z
FL2 = CL * sm.sin(alpha2) * N_v_MB.dot(N.x).subs(u) * (H - dz) * N.z
FL3 = CL * sm.sin(alpha3) * N_v_MB.dot(N.x).subs(u) * (H - dz) * N.z
FL4 = CL * sm.sin(alpha4) * N_v_MB.dot(N.x).subs(u) * (H - dz) * N.z
FL4
5.8.3 Propulsive Force¶
FPmag = sm.symbols('FPmag')
FP = FPmag * N.x
5.8.4 Contact Forces: Subsurface Travel Avoidance¶
Contact collision and frictional forces act on the wheels of the vehicle.
kc, cc, mu, vs = sm.symbols('k_c, c_c, mu, v_s')
P1_B = P1.pos_from(O).dot(N.z).subs(u)
penetration1 = (sm.Abs(P1_B) - P1_B)/2
vertical_force1 = (kc*penetration1**3 - P1_B)*(1-cc*P1.vel(N).dot(N.z).subs(u))
friction_force_x1 = -mu*vertical_force1*((2/(1+sm.exp(-P1.vel(N).dot(N.x).subs(u)/vs))) - 1)
friction_force_y1 = -mu*vertical_force1*((2/(1+sm.exp(-P1.vel(N).dot(N.y).subs(u)/vs))) - 1)
contact_force1 = friction_force_x1*N.x + friction_force_y1*N.y + vertical_force1*N.z
P2_B = P2.pos_from(O).dot(N.z).subs(u)
penetration2 = (sm.Abs(P2_B) - P2_B)/2
vertical_force2 = (kc*penetration2**3 - P2_B)*(1-cc*P2.vel(N).dot(N.z).subs(u))
friction_force_x2 = -mu*vertical_force2*((2/(1+sm.exp(-P2.vel(N).dot(N.x).subs(u)/vs))) - 1)
friction_force_y2 = -mu*vertical_force2*((2/(1+sm.exp(-P2.vel(N).dot(N.y).subs(u)/vs))) - 1)
contact_force2 = friction_force_x2*N.x + friction_force_y2*N.y + vertical_force2*N.z
P3_B = P3.pos_from(O).dot(N.z).subs(u)
penetration3 = (sm.Abs(P3_B) - P3_B)/2
vertical_force3 = (kc*penetration3**3 - P3_B)*(1-cc*P3.vel(N).dot(N.z).subs(u))
friction_force_x3 = -mu*vertical_force3*((2/(1+sm.exp(-P3.vel(N).dot(N.x).subs(u)/vs))) - 1)
friction_force_y3 = -mu*vertical_force3*((2/(1+sm.exp(-P3.vel(N).dot(N.y).subs(u)/vs))) - 1)
contact_force3 = friction_force_x3*N.x + friction_force_y3*N.y + vertical_force3*N.z
P4_B = P4.pos_from(O).dot(N.z).subs(u)
penetration4 = (sm.Abs(P4_B) - P4_B)/2
vertical_force4 = (kc*penetration4**3 - P4_B)*(1-cc*P4.vel(N).dot(N.z).subs(u))
friction_force_x4 = -mu*vertical_force4*((2/(1+sm.exp(-P4.vel(N).dot(N.x).subs(u)/vs))) - 1)
friction_force_y4 = -mu*vertical_force4*((2/(1+sm.exp(-P4.vel(N).dot(N.y).subs(u)/vs))) - 1)
contact_force4 = friction_force_x4*N.x + friction_force_y4*N.y + vertical_force4*N.z
5.9 Kane's Method¶
The model is set up to leverage the accessibility of Kane's method of solving multibody dynamics problems.
kdes = [z1.rhs - z1.lhs, z2.rhs - z2.lhs, z3.rhs - z3.lhs, z4.rhs - z4.lhs]
bogie = me.RigidBody('Bogie', MB, B, mB, (IB, MB))
wing1 = me.RigidBody('Wing_1', MW1, W1, mW, (IW1, MW1))
wing2 = me.RigidBody('Wing_2', MW2, W2, mW, (IW2, MW2))
wing3 = me.RigidBody('Wing_3', MW3, W3, mW, (IW3, MW3))
wing4 = me.RigidBody('Wing_4', MW4, W4, mW, (IW4, MW4))
bodies = [bogie, wing1, wing2, wing3, wing4]
loads = [(MB, G_B + FP),
(MW1, G_W1 + FL1),
(MW2, G_W2 + FL2),
(MW3, G_W3 + FL3),
(MW4, G_W4 + FL4),
(P1, contact_force1),
(P2, contact_force2),
(P3, contact_force3),
(P4, contact_force4),
]
kane = me.KanesMethod(N, (dx, dz, bpitch, broll), (u_dx, u_dz, u_bpitch, u_broll), kd_eqs=kdes)
The holonomic generalized active forces, , and generalized inertia forces, , are computed using Kane's method.
fr, frstar = kane.kanes_equations(bodies, loads=loads)
# fr
# frstar
6. Simulation¶
The vehicle model is validated by means of a simulation, by defining the constants and specifying the initial conditions. One simulation case (maximum levitation height, = 1 meter) is demonstrated for a 50 second run.
The magnetic wings are pitched at 15 degrees each. The coefficient of friction between the wheels and the track surface is chosen to be 0.2. An axial propulsive force of 10 N is applied. The vehicle starts at an initial axial speed of 10 m/s.
sys = System(kane)
sys.constants_symbols
sys.constants = {CL: 50,
FPmag: 10,
H: 1,
IBx: 1.02,
IBy: 19.07,
IBz: 20.04,
IWx: 0.00204587701,
IWy: 0.0982636759,
IWz: 0.0985611947,
alpha1: 0.261799,
alpha2: 0.261799,
alpha3: 0.261799,
alpha4: 0.261799,
cc: 0.1,
g: 9.81,
hb: 0.025,
kc: 5.0e7,
lb: 1.2,
mB: 34.04,
mW: 3.06451,
mu: 0.2, #1.0
vs: 0.01, #0.85
wb: 0.45,
ww: 0.025
}
sys.times = np.linspace(0.0, 50.0, num=1000)
t = me.dynamicsymbols._t
sys.initial_conditions = {dx: 0.0,
dz: 0.1,
bpitch: 0.0,
broll: 0.0,
u_dx: 10.0,
u_dz: 0.0,
u_bpitch: 0.0,
u_broll: 0.0
}
x = sys.integrate()
fig, ax = plt.subplots()
ax.plot(sys.times, x[:, 5])
ax.set_xlabel('{} [s]'.format(sm.latex(t, mode='inline'))); ax.set_ylabel('{} [m/s]'.format(sm.latex(u_dz, mode='inline')));
plt.show()
Vertical speed of the mass-center of the vehicle
fig, ax = plt.subplots()
ax.plot(sys.times, x[:, 6])
ax.set_xlabel('{} [s]'.format(sm.latex(t, mode='inline'))); ax.set_ylabel('{} [rad/s]'.format(sm.latex(u_bpitch, mode='inline')));
# plt.show()
Pitch rate of the Bogie
7. 3D Visualization¶
A 3D animation of the simulation is developed using pythreejs and PyDy (Courtesy of Dr. Jason Moore), to gain more insight into the behavior of the vehicle under different levitation regimes.
from pydy.viz.shapes import Cube, Cylinder, Sphere, Plane
from pydy.viz.visualization_frame import VisualizationFrame
from pydy.viz import Scene
from ipywidgets import Image, Video
import pythreejs as pjs
bogie_shape = Cube(1.2, color='red')
wing1_shape = Cube(0.4, color='green')
wing2_shape = Cube(0.4, color='green')
wing3_shape = Cube(0.4, color='green')
wing4_shape = Cube(0.4, color='green')
v1 = VisualizationFrame('Bogie',
N.orientnew('Bogie', 'Body', [-bpitch, broll, 0], 'YXZ'),
MB,
bogie_shape)
v2 = VisualizationFrame('Wing1',
B.orientnew('Wing1', 'Axis', (alpha1, -B.y)),
MW1.locatenew('M_W_1', (1/6) * lb * B.x),
wing1_shape)
v3 = VisualizationFrame('Wing2',
B.orientnew('Wing2', 'Axis', (alpha1, -B.y)),
MW2.locatenew('M_W_2', (1/6) * lb * B.x),
wing2_shape)
v4 = VisualizationFrame('Wing3',
B.orientnew('Wing3', 'Axis', (alpha1, -B.y)),
MW3.locatenew('M_W_3', -(1/6) * lb * B.x),
wing3_shape)
v5 = VisualizationFrame('Wing4',
B.orientnew('Wing4', 'Axis', (alpha1, -B.y)),
MW4.locatenew('M_W_4', -(1/6) * lb * B.x),
wing4_shape)
scene = Scene(N, O, v1, v2, v3, v4, v5, system=sys)
scene.create_static_html(overwrite=True, silent=True)
bogie_mesh = pjs.Mesh(
pjs.BoxBufferGeometry(1.2, 0.45, 0.025),
pjs.MeshStandardMaterial(color='red'),
name="Bogie"
)
wing1_mesh = pjs.Mesh(
pjs.BoxBufferGeometry(height=0.025, width=0.4, depth=0.025),
pjs.MeshStandardMaterial(color='green'),
name='Wing1'
)
wing2_mesh = pjs.Mesh(
pjs.BoxBufferGeometry(height=0.025, width=0.4, depth=0.025),
pjs.MeshStandardMaterial(color='green'),
name='Wing2'
)
wing3_mesh = pjs.Mesh(
pjs.BoxBufferGeometry(height=0.025, width=0.4, depth=0.025),
pjs.MeshStandardMaterial(color='green'),
name='Wing3'
)
wing4_mesh = pjs.Mesh(
pjs.BoxBufferGeometry(height=0.025, width=0.4, depth=0.025),
pjs.MeshStandardMaterial(color='green'),
name='Wing4'
)
bogie_matrices = v1.evaluate_transformation_matrix(x, list(sys.constants.values()))
wing1_matrices = v2.evaluate_transformation_matrix(x, list(sys.constants.values()))
wing2_matrices = v3.evaluate_transformation_matrix(x, list(sys.constants.values()))
wing3_matrices = v4.evaluate_transformation_matrix(x, list(sys.constants.values()))
wing4_matrices = v5.evaluate_transformation_matrix(x, list(sys.constants.values()))
bogie_track = pjs.VectorKeyframeTrack(
name='scene/Bogie.matrix',
times=list(sys.times),
values=bogie_matrices)
wing1_track = pjs.VectorKeyframeTrack(
name='scene/Wing1.matrix',
times=list(sys.times),
values=wing1_matrices)
wing2_track = pjs.VectorKeyframeTrack(
name='scene/Wing2.matrix',
times=list(sys.times),
values=wing2_matrices)
wing3_track = pjs.VectorKeyframeTrack(
name='scene/Wing3.matrix',
times=list(sys.times),
values=wing3_matrices)
wing4_track = pjs.VectorKeyframeTrack(
name='scene/Wing4.matrix',
times=list(sys.times),
values=wing4_matrices)
bogie_mesh.matrixAutoUpdate = False
wing1_mesh.matrixAutoUpdate = False
wing2_mesh.matrixAutoUpdate = False
wing3_mesh.matrixAutoUpdate = False
wing4_mesh.matrixAutoUpdate = False
bogie_mesh.matrix = bogie_matrices[0]
wing1_mesh.matrix = wing1_matrices[0]
wing2_mesh.matrix = wing2_matrices[0]
wing3_mesh.matrix = wing3_matrices[0]
wing4_mesh.matrix = wing4_matrices[0]
x_arrow = pjs.ArrowHelper(dir=[1, 0, 0], length=2.0, color='blue')
y_arrow = pjs.ArrowHelper(dir=[0, 1, 0], length=2.0, color='red')
z_arrow = pjs.ArrowHelper(dir=[0, 0, 1], length=2.0,color='green')
view_width = 960
view_height = 720
camera = pjs.PerspectiveCamera(position=[1, 1, 1],
aspect=view_width/view_height)
key_light = pjs.DirectionalLight(position=[0, 10, 10])
ambient_light = pjs.AmbientLight()
scene_pjs = pjs.Scene(children=[bogie_mesh, wing1_mesh, wing2_mesh, wing3_mesh, wing4_mesh,
x_arrow, y_arrow, z_arrow,
camera, key_light, ambient_light])
controller = pjs.OrbitControls(controlling=camera)
renderer = pjs.Renderer(camera=camera, scene=scene_pjs, controls=[controller], width=view_width, height=view_height)
renderer
Renderer(camera=PerspectiveCamera(aspect=1.3333333333333333, position=(1.0, 1.0, 1.0), quaternion=(0.0, 0.0, 0…
clip = pjs.AnimationClip(tracks=[bogie_track, wing1_track, wing2_track, wing3_track, wing4_track], duration=sys.times[-1])
action = pjs.AnimationAction(pjs.AnimationMixer(scene_pjs), clip, scene_pjs)
action
AnimationAction(clip=AnimationClip(duration=50.0, tracks=(VectorKeyframeTrack(name='scene/Bogie.matrix', times…
8. Results and Conclusion¶
8.1 Case 1:¶
H = 10 [m]
The vehicle displays extreme instability, with the maximum levitation height set to ten meters. ¶

Figure 7: Vertical speed and vehicle pitch rate for Case 1. ¶
8.2 Case 2:¶
H = 0.5 [m]
The vehicle comes to a halt due to friction, with the maximum levitation height set to half a meter. ¶

Figure 8: Vertical speed and vehicle pitch rate for Case 2. ¶
8.3 Case 3:¶
H = 1 [m]
The vehicle is fairly stable, with the maximum levitation height set to one meter. ¶

Figure 9: Vertical speed and vehicle pitch rate for Case 3. ¶
The vehicle is fairly stable in Case 3, with the maximum levitation height set to 1 meter. This would be the most favorable maximum levitation height among the simulations cases that were run. The magnitudes of the vertical speed and the pitch rate are relatively extremely low values in this case, and further stability of the vehicle system can be ensured by designing appropriate control systems.
9. Further Extensions/Future Work¶
As an extension of this project, the vehicle system has been linearized in order to enable the design of control systems to further stabilize the MagLev vehicle.
9.1 Linearization¶
x = sm.Matrix([u_dx, u_dz, u_bpitch, u_broll, dx, dz, bpitch, broll])
xeq = sm.zeros(8, 1)
f = fr + frstar
# me.find_dynamicsymbols(f), f.shape
kdes_mat = sm.Matrix(kdes)
hol = f.col_join(kdes_mat)
hol.shape # length = 2n --> Holonomic System
dx1, dz1, bpitch1, broll1, udx1, udz1, ubpitch1, ubroll1 = me.dynamicsymbols('d_{x1}, d_{z1}, b_{pitch1}, b_{roll1}, u_{dx1}, u_{dz1}, u_{bpitch1}, u_{broll1}')
xd = sm.Matrix([dx1, dz1, bpitch1, broll1, udx1, udz1, ubpitch1, ubroll1])
# {k: v for k, v in zip(x.diff(), xd)}
hol = hol.subs({k: v for k, v in zip(x.diff(), xd)})
# me.find_dynamicsymbols(hol)
xeq_sub = {k: v for k, v in zip(x, xeq)}
hol_lin = hol.subs(xeq_sub) + hol.jacobian(x).subs(xeq_sub)*(x - xeq)
Mat = hol_lin.jacobian(xd)
xdot = Mat.LUsolve(-(hol_lin - Mat*xd))
A = xdot.jacobian(x)
# A
Future work would involve the development of a high-fidelity model of the vehicle, incorporating additional degrees of freedom, and also the development control systems to ensure stability and efficient control of the MagLev vehicle.