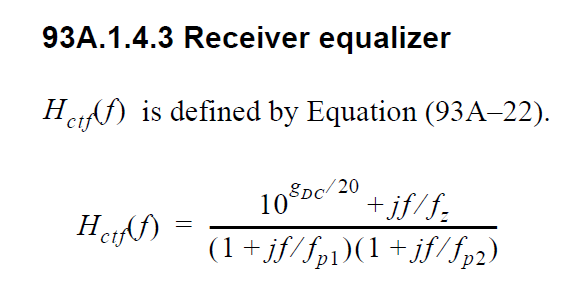Use ML techniques for SERDES CTLE modeling for IBIS-AMI simulation¶
Table of contents:¶
1.Motivation ...¶
2.[Problem Statements](#Problem Statements) ...¶
3.[Generate Data](#Generate Data) ...¶
4.[Prepare Data](#Prepare Data) ...¶
5.[Choose a Model](#Choose a Model) ...¶
6.Training ...¶
7.Prediction ...¶
8.[Reverse Direction](#Reverse Direction) ...¶
9.Deployment ...¶
10.Conclusion ...¶
Motivation:¶
One of SPISim's main service is IBIS-AMI modeling and consulting. In most cases, this happens when IC companies is ready to release simulation model for their customers to do system design. We will then require data either from circuit simulation, lab measurements or data sheet spec. in order to create associated IBIS-AMI model.
Occasionally, we also receive request to provide AMI model for architecture planning purpose. In this situation, there is no data or spec. In stead, the client asks to input performance parameters dynamically (not as preset) so that they can evaluate performance at the architecture level before committing to a certain spec. and design accordingly. In such case, we may need to generate data dynamically based on user's input before it will be fed into existing IBIS-AMI models of same kind.
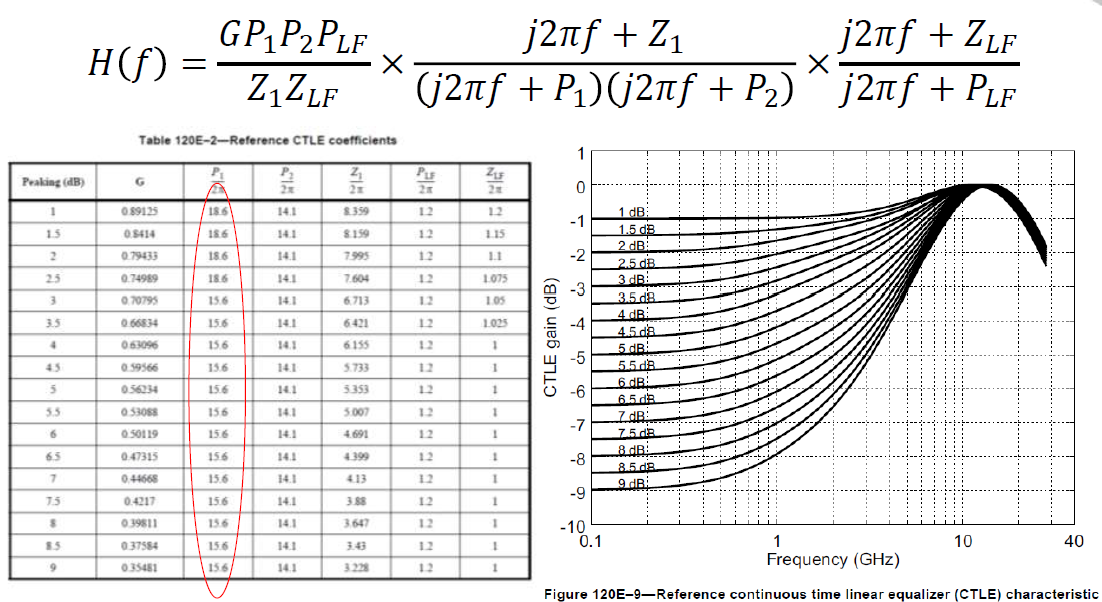
Continues linear equalizer, CTLE, is often used in modern SERDES or even DDR5 design. It is basically a filter in the frequency domain (FD) with various peaking and gain properties. As IBIS-AMI is simulated in the time domain (TD), the core implementations in the model is iFFT to convert into impulse response in TD.
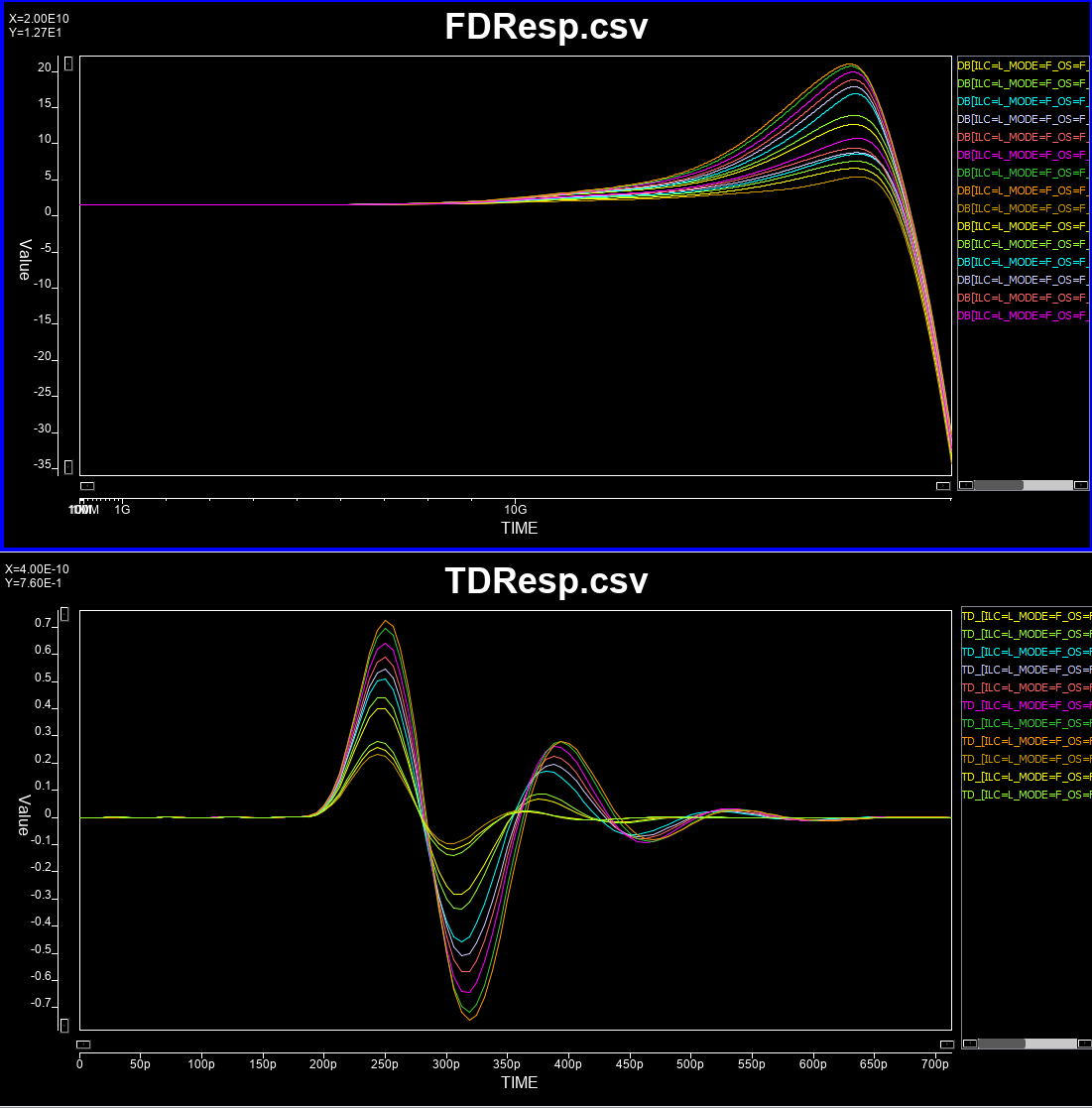
In order to create such CTLE AMI model from user provided spec. on the fly, we would like to avoid time-consuming parameter sweep (in order to match the performance) during runtime of initial set-up call. Thus machine learning techniques may be applied to help use build a prediction model to map input attributes to associated CTLE design parameters so that its FD and TD response can be generated directly. After that, we can feed the data into existing CTLE C/C++ code blocks for channel simulation.
Problem Statement:¶
We would like to build a prediction model such that when user provide a desired CTLE performance parameters, such as DC Gain, peaking frequency and peaking value, this model will map to corresponding CTLE design parameters such as pole and zero locations. Once this is mapped, CTLE frequency response will be generated followed by time-domain impulse response. The resulting IBIS-AMI CTLE model can be used for channel simulation for evaluating such CTLE block's impact in a system... before actual silicon design has been done.
Generate Data:¶
Overview¶
The model to be build is for nominal (i.e. numerical) prediction for about three to six attributes, depending on the CTLE structure, from four input parameters, namely dc gain, peak frequency, peak value and bandwidth. We will sample the input space randomly (as full combinatorial is impractical) then perform measurement programmingly in order generate enough dataset for modeling purpose.
Defing CTLE equations¶
Define sampling points and attributes¶
All these pole and zeros values are continuous (numerical), so a sub-sampling from full solution space will be performed. Once frequency response corresponding to each set of configuration is generated, we will measure is dc gain, peak frequency and value, bandwidth (3dB loss from the peak), and frequencies when 10% and 50% gain between dc and peak values happened. The last two attributes will help us increasing the attributes available when creating the prediction model.
Attributes to be extracted:¶
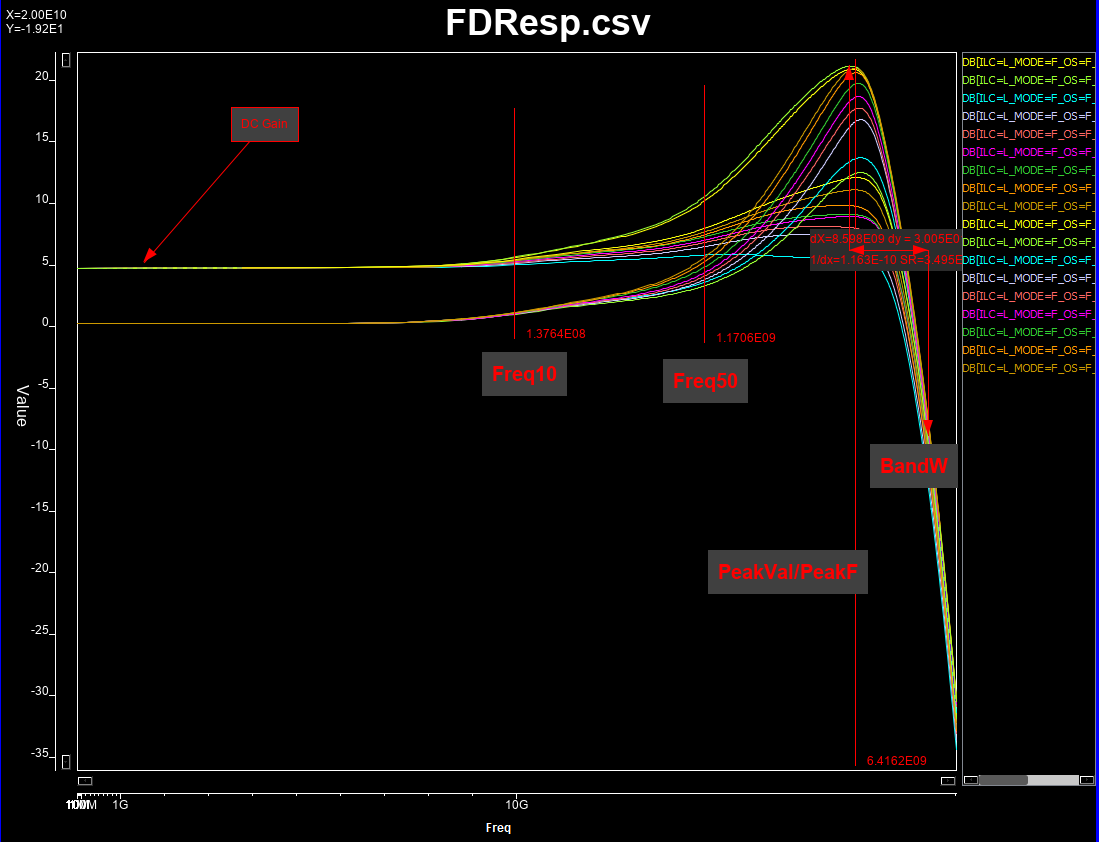
Synthesize and measure data¶
A python script (in order to be used with subsequent Q-learning w/ OpenAI later) has been written to synthesize these frequency response and perform measurement at the same time.
Quantize and Sampling:¶
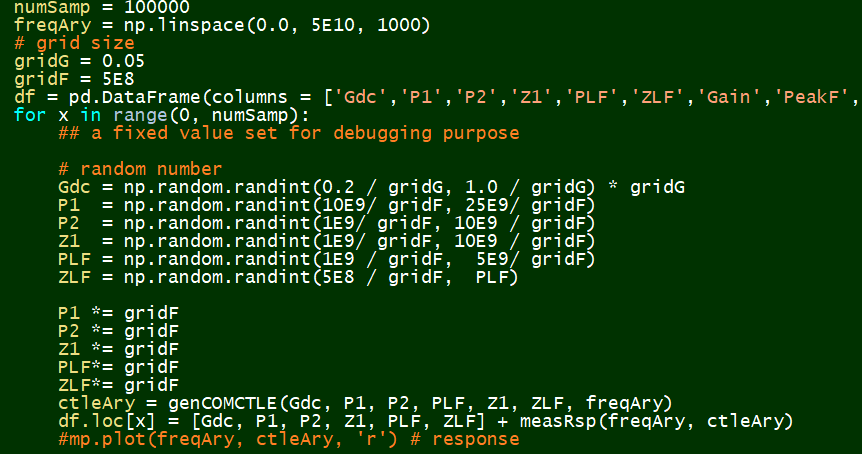
Synthesize:¶
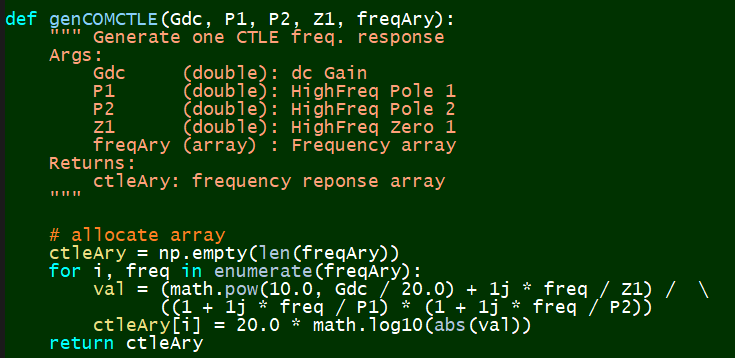
Measurement:¶
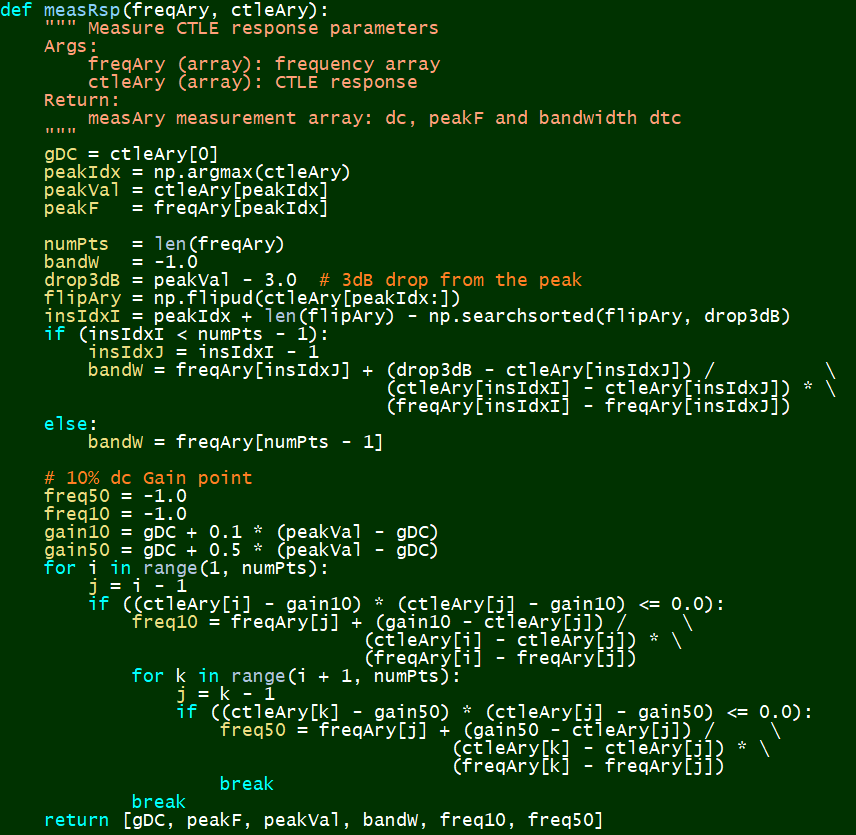
The end results after this data generation phase is a 100,000 points dataset for each of the two CTLE structures. We can now proceed for the prediction modeling.
Prepare Data:¶
## Using COM CTLE as an example below:
# Environment Setup:
import os
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
prjHome = 'C:/Temp/WinProj/CTLEMdl'
workDir = prjHome + '/wsp/'
srcFile = prjHome + '/dat/COM_CTLEData.csv'
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(workDir, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# Read Data
srcData = pd.read_csv(srcFile)
srcData.head()
# Info about the data
srcData.head()
srcData.info()
srcData.describe()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 100000 entries, 0 to 99999 Data columns (total 11 columns): ID 100000 non-null int64 Gdc 100000 non-null float64 P1 100000 non-null float64 P2 100000 non-null float64 Z1 100000 non-null float64 Gain 100000 non-null float64 PeakF 100000 non-null float64 PeakVal 100000 non-null float64 BandW 100000 non-null float64 Freq10 100000 non-null float64 Freq50 100000 non-null float64 dtypes: float64(10), int64(1) memory usage: 8.4 MB
| ID | Gdc | P1 | P2 | Z1 | Gain | PeakF | PeakVal | BandW | Freq10 | Freq50 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 100000.000000 | 100000.000000 | 1.000000e+05 | 1.000000e+05 | 1.000000e+05 | 100000.000000 | 1.000000e+05 | 100000.000000 | 1.000000e+05 | 1.000000e+05 | 1.000000e+05 |
| mean | 49999.500000 | 0.574911 | 1.724742e+10 | 5.235940e+09 | 5.241625e+09 | 0.574911 | 3.428616e+09 | 2.374620 | 1.496343e+10 | 4.145855e+08 | 1.136585e+09 |
| std | 28867.657797 | 0.230302 | 4.323718e+09 | 2.593138e+09 | 2.589769e+09 | 0.230302 | 4.468393e+09 | 3.346094 | 1.048535e+10 | 5.330043e+08 | 1.446972e+09 |
| min | 0.000000 | 0.200000 | 1.000000e+10 | 1.000000e+09 | 1.000000e+09 | 0.200000 | 0.000000e+00 | 0.200000 | 9.965473e+08 | 0.000000e+00 | -1.000000e+00 |
| 25% | 24999.750000 | 0.350000 | 1.350000e+10 | 3.000000e+09 | 3.000000e+09 | 0.350000 | 0.000000e+00 | 0.500000 | 4.770445e+09 | 0.000000e+00 | -1.000000e+00 |
| 50% | 49999.500000 | 0.600000 | 1.700000e+10 | 5.000000e+09 | 5.000000e+09 | 0.600000 | 0.000000e+00 | 0.800000 | 1.410597e+10 | 0.000000e+00 | -1.000000e+00 |
| 75% | 74999.250000 | 0.750000 | 2.100000e+10 | 7.500000e+09 | 7.500000e+09 | 0.750000 | 7.557558e+09 | 2.710536 | 2.386211e+10 | 8.974728e+08 | 2.510339e+09 |
| max | 99999.000000 | 0.950000 | 2.450000e+10 | 9.500000e+09 | 9.500000e+09 | 0.950000 | 1.516517e+10 | 16.731528 | 3.965752e+10 | 1.768803e+09 | 4.678211e+09 |
Seems full justified! Let's plot some distribution...
# Drop the ID column
mdlData = srcData.drop(columns=['ID'])
# plot distribution
mdlData.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots")
plt.show()
Saving figure attribute_histogram_plots
There are abnomal high peaks for Freq10, Freq50 and PeakF. We need to plot the FD data to see what's going on...
Error checking:¶
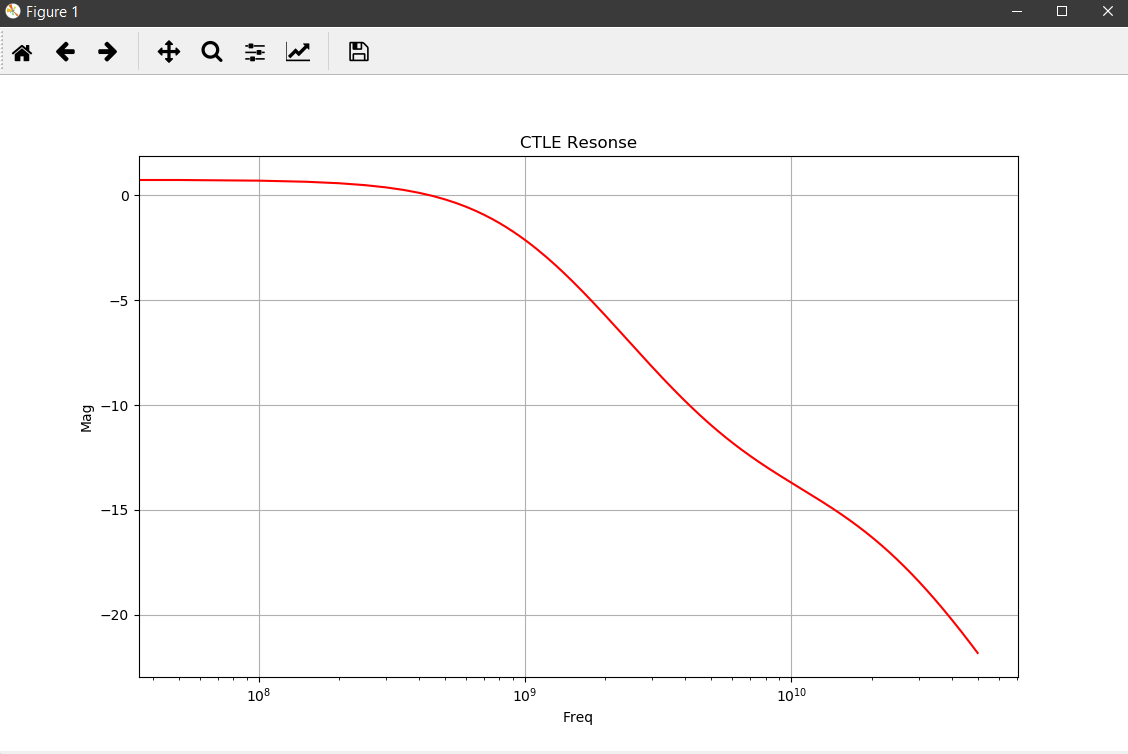
Apparently, this is caused by CTLE without peaking. We can safely remove these data points as they will not be used in actual design.
# Drop those freq peak at the beginning (i.e. no peak)
mdlTemp = mdlData[(mdlData['PeakF'] > 100)]
mdlTemp.info()
# plot distribution again
mdlTemp.hist(bins=50, figsize=(20,15))
save_fig("attribute_histogram_plots2")
plt.show()
<class 'pandas.core.frame.DataFrame'> Int64Index: 41588 entries, 1 to 99997 Data columns (total 10 columns): Gdc 41588 non-null float64 P1 41588 non-null float64 P2 41588 non-null float64 Z1 41588 non-null float64 Gain 41588 non-null float64 PeakF 41588 non-null float64 PeakVal 41588 non-null float64 BandW 41588 non-null float64 Freq10 41588 non-null float64 Freq50 41588 non-null float64 dtypes: float64(10) memory usage: 3.5 MB Saving figure attribute_histogram_plots2
Now the distribution seems good. We can proceed to separate variables (i.e. attributes) and targets
# take this as modeling data from this point
mdlData = mdlTemp
varList = ['Gdc', 'P1', 'P2', 'Z1']
tarList = ['Gain', 'PeakF', 'PeakVal']
varData = mdlData[varList]
tarData = mdlData[tarList]
Choose a Model:¶
We will use Keras for the modeling framework. While it will call Tensorflow on our machine in this case, the GPU is only used for training purpose. We will use (shallow) neural network for modeling as we want to implement the resulting models in our IBIS-AMI model's C++ codes.
from keras.models import Sequential
from keras.layers import Dense, Dropout
numVars = len(varList) # independent variables
numTars = len(tarList) # output targets
nnetMdl = Sequential()
# input layer
nnetMdl.add(Dense(units=64, activation='relu', input_dim=numVars))
# hidden layers
nnetMdl.add(Dropout(0.3, noise_shape=None, seed=None))
nnetMdl.add(Dense(64, activation = "relu"))
nnetMdl.add(Dropout(0.2, noise_shape=None, seed=None))
# output layer
nnetMdl.add(Dense(units=numTars, activation='sigmoid'))
nnetMdl.compile(loss='mean_squared_error', optimizer='adam')
# Provide some info
#from keras.utils import plot_model
#plot_model(nnetMdl, to_file= workDir + 'model.png')
nnetMdl.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_10 (Dense) (None, 64) 320 _________________________________________________________________ dropout_7 (Dropout) (None, 64) 0 _________________________________________________________________ dense_11 (Dense) (None, 64) 4160 _________________________________________________________________ dropout_8 (Dropout) (None, 64) 0 _________________________________________________________________ dense_12 (Dense) (None, 3) 195 ================================================================= Total params: 4,675 Trainable params: 4,675 Non-trainable params: 0 _________________________________________________________________
Training:¶
We will do the 20% training/testing split for the modeling. Note that we need to scale the input attributes to be between 0~1 so that neuron's activation function can be used to differentiate and calculate weights. These scaler will be applied "inversely" when we predict the actual performance later on.
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# Prepare Training (tran) and Validation (test) dataset
varTran, varTest, tarTran, tarTest = train_test_split(varData, tarData, test_size=0.2)
# scale the data
from sklearn import preprocessing
varScal = preprocessing.MinMaxScaler()
varTran = varScal.fit_transform(varTran)
varTest = varScal.transform(varTest)
tarScal = preprocessing.MinMaxScaler()
tarTran = tarScal.fit_transform(tarTran)
Now we can do the model fit:
# model fit
hist = nnetMdl.fit(varTran, tarTran, epochs=100, batch_size=1000, validation_split=0.1)
tarTemp = nnetMdl.predict(varTest, batch_size=1000)
#predict = tarScal.inverse_transform(tarTemp)
#resRMSE = np.sqrt(mean_squared_error(tarTest, predict))
resRMSE = np.sqrt(mean_squared_error(tarScal.transform(tarTest), tarTemp))
resRMSE
Train on 29943 samples, validate on 3327 samples Epoch 1/100 29943/29943 [==============================] - 0s 12us/step - loss: 0.0632 - val_loss: 0.0462 Epoch 2/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0394 - val_loss: 0.0218 Epoch 3/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0218 - val_loss: 0.0090 Epoch 4/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0134 - val_loss: 0.0046 Epoch 5/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0102 - val_loss: 0.0039 Epoch 6/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0090 - val_loss: 0.0036 Epoch 7/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0082 - val_loss: 0.0032 Epoch 8/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0075 - val_loss: 0.0030 Epoch 9/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0071 - val_loss: 0.0027 Epoch 10/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0067 - val_loss: 0.0025 Epoch 11/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0063 - val_loss: 0.0022 Epoch 12/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0059 - val_loss: 0.0020 Epoch 13/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0056 - val_loss: 0.0018 Epoch 14/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0053 - val_loss: 0.0017 Epoch 15/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0050 - val_loss: 0.0015 Epoch 16/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0048 - val_loss: 0.0014 Epoch 17/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0046 - val_loss: 0.0013 Epoch 18/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0045 - val_loss: 0.0012 Epoch 19/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0043 - val_loss: 0.0011 Epoch 20/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0042 - val_loss: 0.0011 Epoch 21/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0041 - val_loss: 9.9891e-04 Epoch 22/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0040 - val_loss: 9.5673e-04 Epoch 23/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0039 - val_loss: 9.1935e-04 Epoch 24/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0038 - val_loss: 8.7424e-04 Epoch 25/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0037 - val_loss: 8.3335e-04 Epoch 26/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0036 - val_loss: 8.0617e-04 Epoch 27/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0035 - val_loss: 7.7511e-04 Epoch 28/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0035 - val_loss: 7.6336e-04 Epoch 29/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0034 - val_loss: 7.4145e-04 Epoch 30/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0034 - val_loss: 7.1555e-04 Epoch 31/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0033 - val_loss: 6.8232e-04 Epoch 32/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0033 - val_loss: 6.8118e-04 Epoch 33/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0033 - val_loss: 6.5987e-04 Epoch 34/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0032 - val_loss: 6.5535e-04 Epoch 35/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0032 - val_loss: 6.4880e-04 Epoch 36/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0032 - val_loss: 6.2126e-04 Epoch 37/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0031 - val_loss: 6.1235e-04 Epoch 38/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0031 - val_loss: 6.0875e-04 Epoch 39/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0030 - val_loss: 5.8204e-04 Epoch 40/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0030 - val_loss: 5.8521e-04 Epoch 41/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0030 - val_loss: 5.8456e-04 Epoch 42/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0030 - val_loss: 5.5742e-04 Epoch 43/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0029 - val_loss: 5.5412e-04 Epoch 44/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0029 - val_loss: 5.5415e-04 Epoch 45/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0029 - val_loss: 5.3159e-04 Epoch 46/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0029 - val_loss: 5.2046e-04 Epoch 47/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0028 - val_loss: 5.1748e-04 Epoch 48/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0028 - val_loss: 5.1205e-04 Epoch 49/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0027 - val_loss: 5.0424e-04 Epoch 50/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0028 - val_loss: 4.9067e-04 Epoch 51/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0027 - val_loss: 4.7902e-04 Epoch 52/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0027 - val_loss: 4.7667e-04 Epoch 53/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0026 - val_loss: 4.6521e-04 Epoch 54/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0026 - val_loss: 4.6684e-04 Epoch 55/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0026 - val_loss: 4.7006e-04 Epoch 56/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0026 - val_loss: 4.5770e-04 Epoch 57/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0025 - val_loss: 4.3075e-04 Epoch 58/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0025 - val_loss: 4.3796e-04 Epoch 59/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0025 - val_loss: 4.3114e-04 Epoch 60/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0025 - val_loss: 4.1051e-04 Epoch 61/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0025 - val_loss: 4.0642e-04 Epoch 62/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0025 - val_loss: 4.1214e-04 Epoch 63/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0025 - val_loss: 3.9472e-04 Epoch 64/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0024 - val_loss: 3.9697e-04 Epoch 65/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0024 - val_loss: 3.8548e-04 Epoch 66/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0024 - val_loss: 3.9030e-04 Epoch 67/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0023 - val_loss: 3.7588e-04 Epoch 68/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0024 - val_loss: 3.6643e-04 Epoch 69/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0023 - val_loss: 3.6973e-04 Epoch 70/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0023 - val_loss: 3.6345e-04 Epoch 71/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0023 - val_loss: 3.5743e-04 Epoch 72/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0023 - val_loss: 3.5294e-04 Epoch 73/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0023 - val_loss: 3.6533e-04 Epoch 74/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0022 - val_loss: 3.5859e-04 Epoch 75/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0022 - val_loss: 3.3832e-04 Epoch 76/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0022 - val_loss: 3.5197e-04 Epoch 77/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0022 - val_loss: 3.4445e-04 Epoch 78/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0022 - val_loss: 3.3888e-04 Epoch 79/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0022 - val_loss: 3.3597e-04 Epoch 80/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0022 - val_loss: 3.2317e-04 Epoch 81/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0021 - val_loss: 3.2205e-04 Epoch 82/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.4191e-04 Epoch 83/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.2288e-04 Epoch 84/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.1419e-04 Epoch 85/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.1307e-04 Epoch 86/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.1795e-04 Epoch 87/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.1200e-04 Epoch 88/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.0641e-04 Epoch 89/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.2401e-04 Epoch 90/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0021 - val_loss: 3.0903e-04 Epoch 91/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 3.1448e-04 Epoch 92/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 3.0788e-04 Epoch 93/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 3.0349e-04 Epoch 94/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 3.0098e-04 Epoch 95/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0020 - val_loss: 3.1119e-04 Epoch 96/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 3.0249e-04 Epoch 97/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 2.8934e-04 Epoch 98/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 2.9429e-04 Epoch 99/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0020 - val_loss: 2.8466e-04 Epoch 100/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0019 - val_loss: 3.0773e-04
0.01786895428237113
Let's see how this neural network learns over different Epoch
# plot history
plt.plot(hist.history['loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Val'], loc='upper right')
plt.show()
Looks quite reasonable. We can save the Keras model now together with scaler for later evaluation.
# save model and architecture to single file
nnetMdl.save(workDir + "COM_nnetMdl.h5")
# also save scaler
from sklearn.externals import joblib
joblib.dump(varScal, workDir + 'VarScaler.save')
joblib.dump(tarScal, workDir + 'TarScaler.save')
print("Saved model to disk")
Saved model to disk
Prediction:¶
Now let's use this model to make some prediction
# generate prediction
predict = tarScal.inverse_transform(tarTemp)
allData = np.concatenate([varTest, tarTest, predict], axis = 1)
allData.shape
headLst = [varList, tarList, tarList]
headStr = ''.join(str(e) + ',' for e in headLst)
np.savetxt(workDir + 'COMCtleIOP.csv', allData, delimiter=',', header=headStr)
Let's take some 50 points and see how the prediction work
# plot some data
begIndx = 100
endIndx = 150
indxAry = np.arange(0, len(varTest), 1)
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,0][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,0][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242d059d390>
# Plot Peak Freq.
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,1][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,1][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242d72df2e8>
# Plot Peak Value
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,2][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,2][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242d5ea39e8>
Reverse Direction:¶
The goal of this modeling is to map performance to CTLE poles and zeros locations. What we just did is the other way around (to make sure such neural network's structure meets our need). Now we needs to reverse the direction for actual modeling. To provide more attributes for better predictions, we will also use frequencies where 10% and 50% gain happened as part of the input attributes.
tarList = ['Gdc', 'P1', 'P2', 'Z1']
varList = ['Gain', 'PeakF', 'PeakVal', 'Freq10', 'Freq50']
varData = mdlData[varList]
tarData = mdlData[tarList]
from keras.models import Sequential
from keras.layers import Dense, Dropout
numVars = len(varList) # independent variables
numTars = len(tarList) # output targets
nnetMdl = Sequential()
# input layer
nnetMdl.add(Dense(units=64, activation='relu', input_dim=numVars))
# hidden layers
nnetMdl.add(Dropout(0.3, noise_shape=None, seed=None))
nnetMdl.add(Dense(64, activation = "relu"))
nnetMdl.add(Dropout(0.2, noise_shape=None, seed=None))
# output layer
nnetMdl.add(Dense(units=numTars, activation='sigmoid'))
nnetMdl.compile(loss='mean_squared_error', optimizer='adam')
# Provide some info
#from keras.utils import plot_model
#plot_model(nnetMdl, to_file= workDir + 'model.png')
nnetMdl.summary()
_________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense_13 (Dense) (None, 64) 384 _________________________________________________________________ dropout_9 (Dropout) (None, 64) 0 _________________________________________________________________ dense_14 (Dense) (None, 64) 4160 _________________________________________________________________ dropout_10 (Dropout) (None, 64) 0 _________________________________________________________________ dense_15 (Dense) (None, 4) 260 ================================================================= Total params: 4,804 Trainable params: 4,804 Non-trainable params: 0 _________________________________________________________________
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
# Prepare Training (tran) and Validation (test) dataset
varTran, varTest, tarTran, tarTest = train_test_split(varData, tarData, test_size=0.2)
# scale the data
from sklearn import preprocessing
varScal = preprocessing.MinMaxScaler()
varTran = varScal.fit_transform(varTran)
varTest = varScal.transform(varTest)
tarScal = preprocessing.MinMaxScaler()
tarTran = tarScal.fit_transform(tarTran)
# model fit
hist = nnetMdl.fit(varTran, tarTran, epochs=100, batch_size=1000, validation_split=0.1)
tarTemp = nnetMdl.predict(varTest, batch_size=1000)
#predict = tarScal.inverse_transform(tarTemp)
#resRMSE = np.sqrt(mean_squared_error(tarTest, predict))
resRMSE = np.sqrt(mean_squared_error(tarScal.transform(tarTest), tarTemp))
resRMSE
Train on 29943 samples, validate on 3327 samples Epoch 1/100 29943/29943 [==============================] - 0s 15us/step - loss: 0.0800 - val_loss: 0.0638 Epoch 2/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0578 - val_loss: 0.0457 Epoch 3/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0458 - val_loss: 0.0380 Epoch 4/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0408 - val_loss: 0.0344 Epoch 5/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0378 - val_loss: 0.0317 Epoch 6/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0354 - val_loss: 0.0299 Epoch 7/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0340 - val_loss: 0.0287 Epoch 8/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0327 - val_loss: 0.0276 Epoch 9/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0315 - val_loss: 0.0265 Epoch 10/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0303 - val_loss: 0.0254 Epoch 11/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0293 - val_loss: 0.0244 Epoch 12/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0284 - val_loss: 0.0235 Epoch 13/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0274 - val_loss: 0.0225 Epoch 14/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0266 - val_loss: 0.0215 Epoch 15/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0257 - val_loss: 0.0202 Epoch 16/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0245 - val_loss: 0.0189 Epoch 17/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0235 - val_loss: 0.0175 Epoch 18/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0223 - val_loss: 0.0160 Epoch 19/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0213 - val_loss: 0.0146 Epoch 20/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0202 - val_loss: 0.0135 Epoch 21/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0193 - val_loss: 0.0125 Epoch 22/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0186 - val_loss: 0.0117 Epoch 23/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0179 - val_loss: 0.0109 Epoch 24/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0171 - val_loss: 0.0104 Epoch 25/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0167 - val_loss: 0.0099 Epoch 26/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0163 - val_loss: 0.0094 Epoch 27/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0156 - val_loss: 0.0090 Epoch 28/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0154 - val_loss: 0.0087 Epoch 29/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0151 - val_loss: 0.0084 Epoch 30/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0146 - val_loss: 0.0081 Epoch 31/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0143 - val_loss: 0.0077 Epoch 32/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0139 - val_loss: 0.0074 Epoch 33/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0138 - val_loss: 0.0072 Epoch 34/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0135 - val_loss: 0.0071 Epoch 35/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0132 - val_loss: 0.0069 Epoch 36/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0131 - val_loss: 0.0068 Epoch 37/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0130 - val_loss: 0.0066 Epoch 38/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0129 - val_loss: 0.0065 Epoch 39/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0127 - val_loss: 0.0063 Epoch 40/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0124 - val_loss: 0.0062 Epoch 41/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0122 - val_loss: 0.0061 Epoch 42/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0122 - val_loss: 0.0059 Epoch 43/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0120 - val_loss: 0.0059 Epoch 44/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0119 - val_loss: 0.0057 Epoch 45/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0118 - val_loss: 0.0057 Epoch 46/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0117 - val_loss: 0.0056 Epoch 47/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0115 - val_loss: 0.0055 Epoch 48/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0114 - val_loss: 0.0055 Epoch 49/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0114 - val_loss: 0.0055 Epoch 50/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0112 - val_loss: 0.0053 Epoch 51/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0111 - val_loss: 0.0052 Epoch 52/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0112 - val_loss: 0.0052 Epoch 53/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0111 - val_loss: 0.0052 Epoch 54/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0109 - val_loss: 0.0051 Epoch 55/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0108 - val_loss: 0.0050 Epoch 56/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0107 - val_loss: 0.0049 Epoch 57/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0107 - val_loss: 0.0050 Epoch 58/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0107 - val_loss: 0.0049 Epoch 59/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0106 - val_loss: 0.0048 Epoch 60/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0104 - val_loss: 0.0047 Epoch 61/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0103 - val_loss: 0.0046 Epoch 62/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0102 - val_loss: 0.0046 Epoch 63/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0103 - val_loss: 0.0046 Epoch 64/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0102 - val_loss: 0.0045 Epoch 65/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0101 - val_loss: 0.0044 Epoch 66/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0101 - val_loss: 0.0044 Epoch 67/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0100 - val_loss: 0.0045 Epoch 68/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0098 - val_loss: 0.0043 Epoch 69/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0098 - val_loss: 0.0043 Epoch 70/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0098 - val_loss: 0.0043 Epoch 71/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0097 - val_loss: 0.0042 Epoch 72/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0096 - val_loss: 0.0043 Epoch 73/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0096 - val_loss: 0.0041 Epoch 74/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0094 - val_loss: 0.0042 Epoch 75/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0094 - val_loss: 0.0041 Epoch 76/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0094 - val_loss: 0.0041 Epoch 77/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0093 - val_loss: 0.0040 Epoch 78/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0094 - val_loss: 0.0040 Epoch 79/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0093 - val_loss: 0.0040 Epoch 80/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0092 - val_loss: 0.0039 Epoch 81/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0091 - val_loss: 0.0039 Epoch 82/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0091 - val_loss: 0.0039 Epoch 83/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0091 - val_loss: 0.0039 Epoch 84/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0091 - val_loss: 0.0038 Epoch 85/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0090 - val_loss: 0.0039 Epoch 86/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0089 - val_loss: 0.0038 Epoch 87/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0089 - val_loss: 0.0038 Epoch 88/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0088 - val_loss: 0.0037 Epoch 89/100 29943/29943 [==============================] - 0s 4us/step - loss: 0.0088 - val_loss: 0.0037 Epoch 90/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0087 - val_loss: 0.0037 Epoch 91/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0087 - val_loss: 0.0037 Epoch 92/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0086 - val_loss: 0.0036 Epoch 93/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0087 - val_loss: 0.0037 Epoch 94/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0086 - val_loss: 0.0036 Epoch 95/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0084 - val_loss: 0.0036 Epoch 96/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0086 - val_loss: 0.0036 Epoch 97/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0085 - val_loss: 0.0036 Epoch 98/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0085 - val_loss: 0.0035 Epoch 99/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0085 - val_loss: 0.0035 Epoch 100/100 29943/29943 [==============================] - 0s 3us/step - loss: 0.0084 - val_loss: 0.0034
0.0589564154176633
# plot history
plt.plot(hist.history['loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Val'], loc='upper right')
plt.show()
# Separated Keras' architecture and synopse weight for later Cpp conversion
from keras.models import model_from_json
# serialize model to JSON
nnetMdl_json = nnetMdl.to_json()
with open("COM_nnetMdl_Rev.json", "w") as json_file:
json_file.write(nnetMdl_json)
# serialize weights to HDF5
nnetMdl.save_weights("COM_nnetMdl_W_Rev.h5")
# save model and architecture to single file
nnetMdl.save(workDir + "COM_nnetMdl_Rev.h5")
print("Saved model to disk")
# also save scaler
from sklearn.externals import joblib
joblib.dump(varScal, workDir + 'Rev_VarScaler.save')
joblib.dump(tarScal, workDir + 'Rev_TarScaler.save')
Saved model to disk
['C:/Temp/WinProj/CTLEMdl/wsp/Rev_TarScaler.save']
# generate prediction
predict = tarScal.inverse_transform(tarTemp)
allData = np.concatenate([varTest, tarTest, predict], axis = 1)
allData.shape
headLst = [varList, tarList, tarList]
headStr = ''.join(str(e) + ',' for e in headLst)
np.savetxt(workDir + 'COMCtleIOP_Rev.csv', allData, delimiter=',', header=headStr)
# plot Gdc
begIndx = 100
endIndx = 150
indxAry = np.arange(0, len(varTest), 1)
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,0][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,0][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242ccefe1d0>
# Plot P1
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,1][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,1][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242ccc7c470>
# Plot P2
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,2][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,2][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242d6f15dd8>
# Plot Z1
plt.scatter(indxAry[begIndx:endIndx], tarTest.iloc[:,3][begIndx:endIndx])
plt.scatter(indxAry[begIndx:endIndx], predict[:,3][begIndx:endIndx])
<matplotlib.collections.PathCollection at 0x242ccbaa978>
It seems this "reversed" neural network also work reasonably well. We will further fine-tune later on.
Deployment:¶
Now that we have trained model in Keras' .h5 format, we can translate this model into corresponding cpp codes using Keras2Cpp:

Its github repository is here: Keras2Cpp
Resulting file can be compiled together with keras_model.cc, keras_model.h in our AMI library.
Conclusion:¶
In this post/notebook, we explore the flow to create a neural network based model for CTLE's parameter prediction. Data science techniques have been used. The resulting Keras' model is then converted into C++ code for implementation in our IBIS-AMI library. With this performance based CTLE model, our user can run channel simulation before committing actual silicon design.