1. UVOD¶
Difrakcija se može definisati kao svaka devijacija u prostiranju svjetlosnog zraka od pravolinijske putanje, koja nije uzorkovana refleksijom ili refrakcijom [1]. Difrakcija nastaje kada elektromagnetni talas naiđe na neku prepreku ili neki otvor. Stoljećima je bilo poznato da svjetlosni zraci, prolazeći kroz mali otvor u neporovidnoj prepreci ne formiraju oštru sjenu na udaljenom zaslonu. Ovakva pojava se mogla objasniti samo uz pretpostavku da se svjetlost ima talasna svojstva. Pojavu difrakcije prvi je zapazio Francesco Grimaldi (1655.), a početkom 19. vijeka difrakcija je korištena kao jedan od dokaza u debati o prirodi svjetlosti. Teorija difrakcije svjetlosti je razvijana od strane Hygensa, Fresnela, Kirchoffa i Sommerfelda. Pri rješavanju problema obuhvaćenog ovim projektom biće korištena tzv. skalarana teorija difrakcije, koja uvodi izvjesne aproksimacije. Npr. biće zanemarena moguća kapliranja električnog i magnetnog polja. Ovakva aproksimacija je dobra kada se difrakcija posmatra kroz otvor koji je značajno veći od talasne dužine svjetlosti, te kada se difrakciono polje računa na većim udaljenostima od zaslona.
Difrakciju možemo podijeliti u dvije kategorije: Fraunhferovu i Fresnelovu difrakciju. U optici, Fresnelova difrakcija se javlja neposredno iza otvora kroz koji prolazi svjetlosni talas ("near-field"), pri čemu oblik i veličina difrakcionog uzorka ovise o udaljenosti zaslona na kojem nastaju. Sa povećanjem udaljenosti otvor - zaslon, difraktovani talasi se približavaju ravanskim prema obliku pri čemu se javlja Fraunhoferova ("far-field") difrakcija. U tom slučaju, oblik difrakcionog uzorka je uvijek isti, a mijenja se samo njegova veličina u zavisnosti od udaljenosti od otvora[2]. Fraunhoferova difrakcija se javlja kada je tzv. Fresnelov broj* veoma mali ($F \ll 1$), a Fresnelova difrakcija se javlja u slučaju kada je $F > 1.$ Pojava difrakcije svjetlosti i skalarna teorija su detaljno pojašnjeni u [3].
Fraunhoferova difrakcija je matematički jednostavnija i difrakciona slika se može predstaviti kao dvodimenzionalna Fourierova transformacija prigodno odabrane funkcije koja odgovara otvoru na kojem dolazi do difrakcije. Naprimjer, ako govorimo o difrakciji na kvadratnom otvoru, Fraunhoferov uzorak se može prikazati kao produkt kvadrata dviju $sinc$ funkcija, koje uključuju talasnu dužinu svjetlosti, koordinate ravni zaslona i udaljenost otvora od zaslona [3]. S druge strane, Fresnelova difrakcija je značajno složenija, jer obično posmatrani talasni front nije ravanski. U ovom slučaju se analitičko rješenje može potražiti preko odgovarajućih integrala, poznatih kao Helmoltz-Kirchoff ili Rayleigh-Sommerfeld integrali [4].
Problem difrakcije spada među složenije probleme optike, i strogo tačna rješenja su dostupna za ograničen broj konkretnih problema (sa određenim tipovima otvora). Uglavnom se to odnosi na dvodimenzionalne probleme. Razvojem računarske tehnologije, problem difrakcije je postalo moguće modelirati korištenjem tzv. Fourierove transformacije.
$*$ $F=\dfrac{w^2}{\lambda z}$, $w$- dimenzije otvora, $\lambda$ - talasna dužina svjetlosti, $z$ - udaljenost otvor - zaslon
Difrakcija svjetlosti i Fourierova transformacija¶
Prema skalarnoj teoriji difrakcije, vrijednost električnog polja u tački $(x,y)$ u ravni koja je paralelna sa ravni otvora $(\xi, \eta)$ koja se nalazi na udaljenosti $z$ je prema Fresnelovoj aproksimaciji data kao: $$ U(x,y)=\dfrac{e^{ikz}}{i\lambda z} e^{\frac{ik}{2z}(x^2+y^2)} \int \int_{-\infty}^{+\infty} \Big\{ U(\xi,\eta) e^{\frac{ik}{2z}(\xi^2+\eta^2)} \Big\} e^{-i \frac{2 \pi}{\lambda z}(x \xi+y \eta)} d \xi d \eta. $$
Iz jednačine je vidljivo da se raspodjela vektora električnog polja na zaklonu može posmatrati kao dvodimenzionalna Fourierova transformacija izraza u vitičastim zagradama, tj.:
$$ U(x,y,z)=A(x,y,z) \textit{F} \Big\{ U(\xi,\eta,0) e^{\frac{i\pi}{\lambda z}(\xi^2+\eta^2)} \Big\}_{(f_x,f_y)} $$gdje je $$ A(x,y,z)= \dfrac{e^{ikz}}{i\lambda z} e^{\frac{i\pi}{\lambda z}(x^2+y^2)}. $$ $U(\xi,\eta)$ predstavlja raspodjelu električnog polja na difrakcionom otvoru, a $f_x$ i $f_y$ prosotorne frekvencije date sa $f_x=\frac{x}{\lambda z}$ i $f_y=\frac{y}{\lambda z}.$
U Fraunhoferovoj aproksimaciji raspodjela električnog polja je data sa: $$ U(x,y)=\dfrac{e^{ikz}}{i\lambda z} e^{\frac{ik}{2z}(x^2+y^2)} \int \int_{-\infty}^{+\infty} \Big\{ U(\xi,\eta) \Big\} e^{-i \frac{2 \pi}{\lambda z}(x \xi+y \eta)} d \xi d \eta ,$$ odnosno preko Fourierove transformacije: $$ U(x,y,z)=A(x,y,z) \textit{F} \Big\{ U(\xi,\eta,0) \Big\}_{(f_x,f_y)}. $$
Raspodjela intenziteta svjetlosnog talasa na zaklonu je data izrazom:
$$I=\dfrac{1}{\lambda^2 z^2} \left|\textit{F} \Big\{ U(\xi,\eta,0) \Big\}\right|^2_{f_x,f_y}. $$U ovom izvještaju biće prikazana raspodjela intenziteta svjetlosti na zaklonu za nekoliko tipova otvora (jednostruka i dvostruka pukotina, kružni otvor, kvadratni otvor) za obje aproksimacije - Fraunfoerovu ("far field") i Fresnelovu ("near field").
FOURIEROVA TRANSFORMACIJA¶
Fourierova transformacija kontinuirane funkcije $f(x)$ je definisana sa: $$ \begin{equation} f(\nu)=\mathcal{F}[f(x)](\nu)=\int_{-\infty}^{\infty}f(t)e^{-2\pi i\nu t}dt. \end{equation}$$ gdje je $\nu$ - prostorna frekvencija. Posmatrajmo generalizaciju na slučaj diskretne funkcije, tj. kada je $f(x)\rightarrow f(x_k) \equiv f_k$, gdje je $x_k\equiv k\Delta,$ sa $k=0,1,2,...,N-1.$ Tada se diskretna Fourierova transformacija $F_n=\mathcal{F}_k \big[ \big \{f_k \big \}_{k=0}^{N-1}\big](n)$ može zapisati u obliku: $$ F_n=\sum_{k=0}^{N-1}f_k e^{-2\pi i n k/N} \quad n=0,1,2,...,N-1 .$$
Inverzna Fourireova tranformacija $f_k=\mathcal{F}_n^{-1} \big[ \big \{F_n \big \}_{n=0}^{N-1}\big](k)$ će imati oblik: $$f_k=\dfrac{1}{N}\sum_{n=0}^{N-1}F_n e^{2\pi ikn/N}.$$
Diskretna Fourierova transformacija (DFT) je vrlo korisna jer otkriva svaku periodičnost u ulaznim podacima, kao i relativnu težinu svake pojedinačne komponente koja čini ulazni signal. U opštem slučaju, DFT realnog niza podataka daje niz kompleksnih vrijednosti jednake dužine.
Transformacija iz $f_n\rightarrow F_k$ je translacija sa konfiguracijskog u frekvencijski prostor i vrlo je korisna kako za istraživanje spektra snage signala tako i za određene transformacije problema koje dovode do efikasnijih proračuna.
Prema izrazu za DFT sa aspekta proračuna radi se o linearnoj operaciji - proizvod matrice sa vektorom: $$ \vec{F}=M\cdot \vec{f} $$ gdje je matrica $M$ data kao: $$ M_{kn}=e^{-i2\pi kn/N}. $$
Direktno izračunavanje ovakve matrice teče vrlo sporo jer zahtjeva veliki broj kompleksnih proračuna.Upravo zbog toga je razvijena tzv. Brza Fourierova transformacija (Fast Fourier Transform - FFT) koja značajno reducira broj proračuna. Npr. za slučaj $N=10^6$ tačaka vrijeme je sa 20 sati redukovano na 50 ms u programskom jeziku Python koji je korišten za rješavanje ovog problema.
Kako radi FFT?¶
Brza Fourierova transfromacija je posebno efikasni algoritam za izvođenje diskretne Fourierove transformacije diskretnog niza podataka. Algoritam za brzu Furijeovu transformaciju prvi su razvili Cooley i Tukey 1965. godine [5], iako je još Gauss razradio kritične korake faktorizacije 150 godina ranije.
Brza Furijeova transformacija je algoritam za diskretnu Fourierivou transformaciju koji reducira broj potrebnih kompjutacija potrebnih za $N$ tačaka, sa $2N^2$ na $2Nlog_2N$ [6]. FFT je jedan od najvažnijih algoritama u obradi signala i analizi podataka.
U razvoju FFT algoritma vrlo važnu ulogu igraju simetrije koje postoje u problemu koji se rješava. Ako je moguće analitički dokazati da jedan dio problema ima jednostavnu vezu sa drugim, onda se jedan proračun može primjeniti na oba djela, umjesto zasebnog računanja, čime se štedi vrijeme računanja. Cooley i Tukey su upravo iskoristili ovaj pristup pri razvoju FFT algortima.
Da bi vidjeli kako radi FFT algoritam, pođimo od vrijednosti $F_{N+k}$ iz izraza za DFT:
$$\begin{equation} \begin{split} F_{N+n}{} &=\sum_{k=0}^{N-1}f_k e^{-i2\pi (N+n)k/N} \\ & =\sum_{k=0}^{N-1}f_k e^{-i2\pi k}e^{-i2\pi nk/N} \\ & =\sum_{k=0}^{N-1}f_k e^{-i2\pi nk/N} \end{split} \end{equation}$$gdje je $e^{-i2\pi k}=1.$
Posljednja relacije pokazuje simetričnost DFT: $$ F_{N+n}=F_n$$ što vrijedi za ostale članove u $F_n$: $$ F_{n+zN}=F_n $$ za bilo koji cijeli broj $z.$ Ova simetričnost se može iskoristiti za brže računanje DFT. Cooley i Tukey su u svome radu pokazali da je DFT proračun moguće razdvojiti u dva manja dijela. Naime, iz definicije DFT imamo da je: $$ \begin{equation} \begin{split} F_n{} & =\sum_{k=0}^{N-1}f_k e^{-i2\pi k n/N} \\ & =\sum_{m=0}^{N/2-1}f_{2m} e^{-i2\pi (2m) n/N} + \sum_{m=0}^{N/2-1}f_{2m+1} e^{-i2\pi (2m+1) n/N} \\ & = \sum_{m=0}^{N/2-1}f_{2m} e^{-i2\pi m n/(N/2)} + e^{-i2\pi n/N}\sum_{m=0}^{N/2-1}f_{2m+1} e^{-i2\pi m n/(N/2)} \end{split} \end{equation} $$ Ako uvedemo oznake $$\epsilon_n=\sum_{m=0}^{N/2-1}f_{2m} e^{-i2\pi m n/(N/2)}$$ $$\mathcal{o}_n= \sum_{m=0}^{N/2-1}f_{2m+1} e^{-i2\pi m n/(N/2)}$$ $$w=e^{-i2\pi /N}$$ posljednja linija se može pisati skraćeno kao: $$ F_n=\epsilon_n + w^n \mathcal{o}_n $$ Intersantna i korisna posljedica ovakvog zapisa je što se lako može pokazati da je: $$ F_{n+\frac{N}{2}}=\epsilon_n-w^n \mathcal{o}_n. $$ Vidimo da smo jednu diskretnu Fourierova transformaciju razdvojili na dva člana, koja imaju isti oblik kao i izraz za DFT, s tim što se indeksiranje vrši po parnim članovima ($\epsilon_n)$, odnosno neparnim članovima ($\mathcal{o}_n).$ Svaki član i dalje sadrži (N/2)*N koraka (operacija), odnosno ukupno $N^2.$ Trik je u korištenju simetrija koje postoje u svakom od ovih članova. Kako je opseg $n$ od 0 do N, a opseg $m$ od 0 do M=N/2, vidimo da je u svakom od podproblema broj kompjutacija prepolovljen, tako da je broj operacija sveden sa $\mathcal{O}[N^2]$ na $\mathcal{O}[M^2].$ Algoritam jednom izračuna vrijednost $\epsilon_n$ i $\mathcal{o}_n$, a zatim te vrijednosti iskoristi kako bi dobio vrijednosti za $F_n$ i $F_{n+N/2}.$ Na ovaj način, umjesto dvije imamo jednu kompleksnu multiplikaciju (računanje eksponencijalnog člana) u algoritmu.
Ako se ovakva procedura nastavi sve dok novi članovi (manji) imaju parne vrijednosti $M$, problem računanja DFT se može učiniti mnogo efikasnijim. Postupak dijeljenja je moguć sve dok novi članovi ne budu dovoljno mali da više nema koristi od njihovog daljeg smanjivanja. U asimptotskom slučaju, za FFT algoritam potreban broj operacija je $\mathcal{O}[NlogN].$
Navedena procedura (tzv. radix-2 decimation) u Cooley-Tukey FFT algoritmu je poznata pod imenom dijagram leptira.
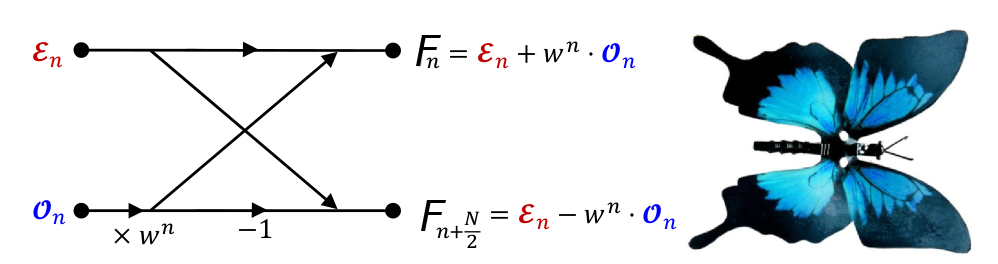
Konkretno, ako imamo problem u N=8 tačaka, FFT algoritam se može uporediti sa DFT preko sljedećeg grafikona.
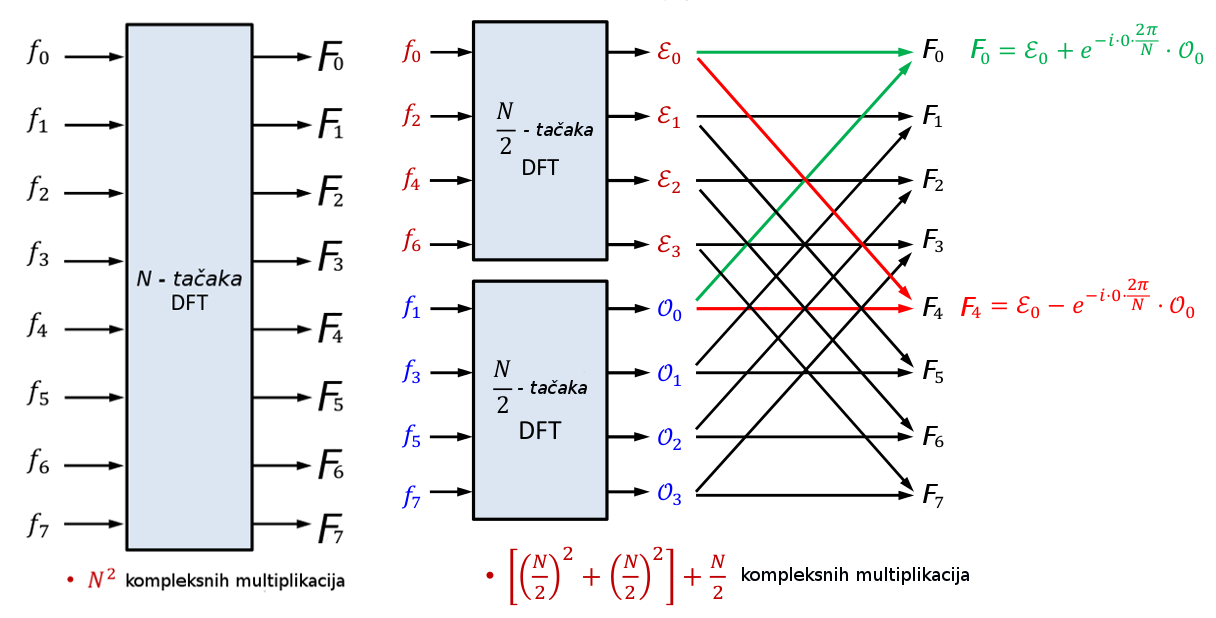
U navedenom primjeru se dva DFT algoritma mogu dalje podijeliti na četiri DFT algoritama koji bi se računali u N/4 tačaka. Zbog toga ovakav algoritam zahtjeva da se problem riješava u $N=2^n$ tačaka, pri čemu se decimizacija može izvesto $n=log_2N$ puta, odnosno broj kompleksnih multiplikacija će biti $N/2(log_2N)$. Gledano kroz brojke, prednost FFT algoritma nad klasičnim DFT je vidljiva u narednoj tabeli.
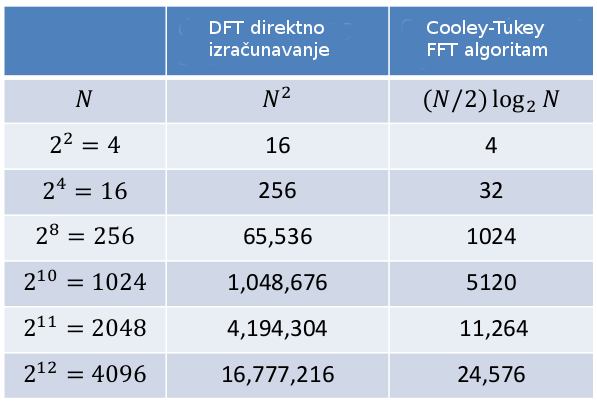
Tokom proteklih decenija FFT algoritam je razvijan i usavršavan. Izdvajaju se FFTPACK(FFT99 & FFT991), NCAR FFTPACK, FFTW i drugi. Programski jezik Python sadrži gotove algoritme za računanje FFT, koje su razvijane i optimizirane kroz Fortranski FFTPACK. Ovakav algoritam postiže velike brzine računanja zahvaljujući optimizaciji broja multiplikacija eksponencijalnih članova, tj. činjenici da se svaki proračun ponovo iskorištava tamo gdje je to moguće.
3. Brza Fourierova transformacija u Pythonu¶
Zbog značaja FFT u mnogim poljima nauke i inžinjerstva, Python sadrži mnoge standardne alate i dodatke koji služe za računanje FFT algoritma. Numpy i SciPy paketi imaju dodatke sa testiranim algoritmima iz FFTPACK biblioteke. Naredbe kojima se pozivaju odogovarajući podmoduli su numpy.fft, odnosno scipy.fftpack.
Poređenjem vremena potrebnog za izravno računanje DFT-a naspram vremena za FFT, za slučaj jednostavnog problema sa $N=10^6$ elemenata, potrebno je dvadesetak sati za DFT algoritam, dok FFT u Pythonu isti račun izvrši za 50 ms.
Rezultati¶
3.1. Fraunhoferova difrakcija¶
a) Difrakcija na kružnoj i kvadratnoj pukotini¶
Na slici su prikazani difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju Fraunhoferove difrakcije na dvodimenzionalnom otvoru (kružni i kvadratni). Talasna dužina upadne svjetlosti je 632 nm, veličina otvora je 0.05 X 0.05 mm (za kvadratni), odnosno prečnik 0.05 mm za kružni otvor, te udaljenost od otvora do zaslona 100 mm. Broj tačaka u kojima se računao FFT je 1048 X 1048.
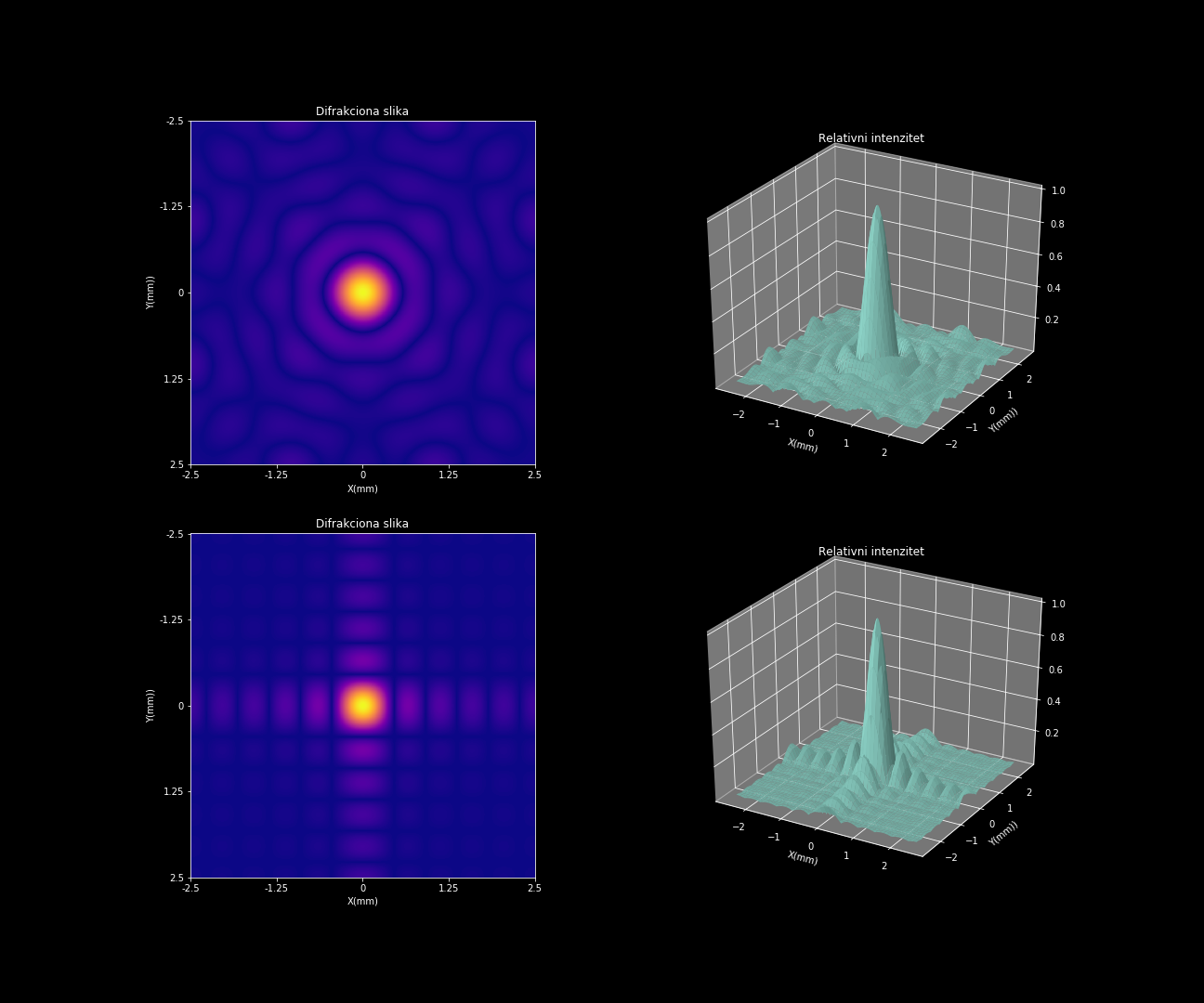
b) Difrakcija na jednostrukoj pukotini¶
Relativna veličina pukotine, difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju difrakcije na jednostrukoj pukotini. Talasna dužina svjetlosti je 632 nm. Vrijednosti širine pukotine i udaljenosti zaslona od otovora su prikazani na slici.
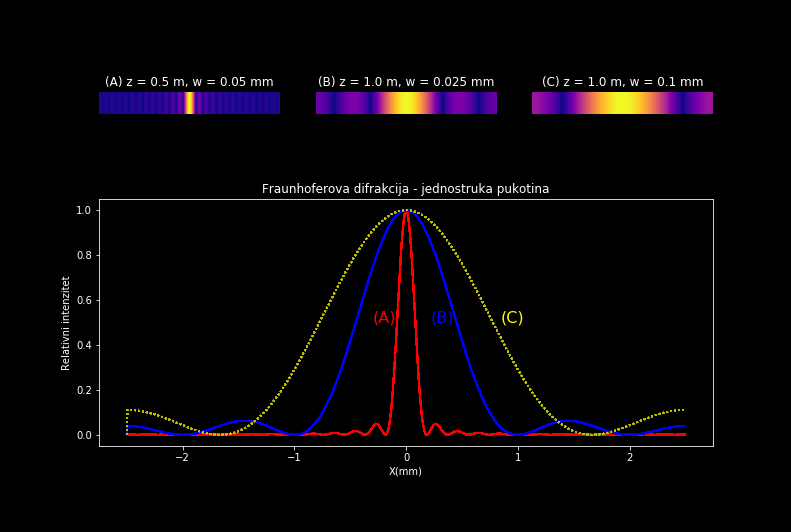
c) Difrakcija na dvostrukoj pukotini¶
Relativna veličina pukotine, difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju difrakcije na dvostrukoj pukotini. Talasna dužina svjetlosti je 632 nm. Vrijednosti polovine širine svake od pukotina i udaljenosti zaslona od otovora su prikazani na slici.
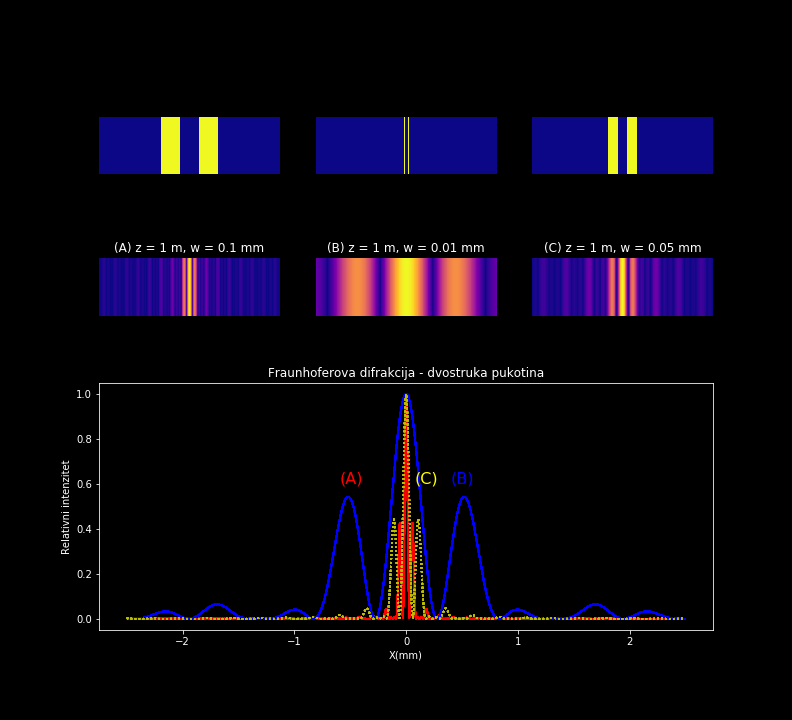
3.2. Fresnelova difrakcija¶
a) Difrakcija na kružnoj i kvadratnoj pukotini¶
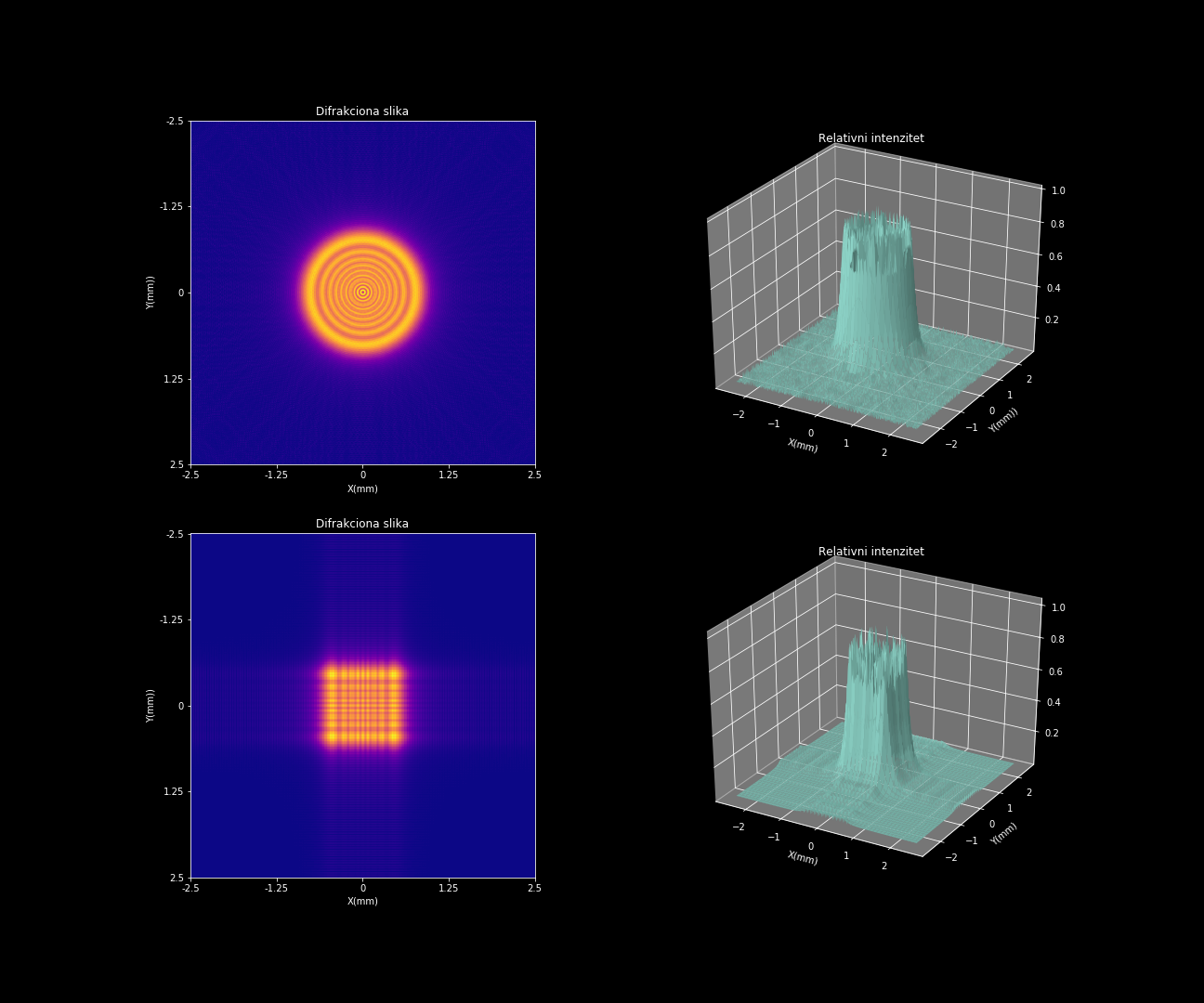
Na slici su prikazani difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju Fresnelove difrakcije na dvodimenzionalnom otvoru (kružni i kvadratni). Talasna dužina upadne svjetlosti je 632 nm, veličina otvora je 0.67 X 0.67 mm (za kvadratni), odnosno prečnik 1.0 mm za kružni otvor, te udaljenost od otvora do zaslona 200 mm. Broj tačaka u kojima se računao FFT je 1048 X 1048.
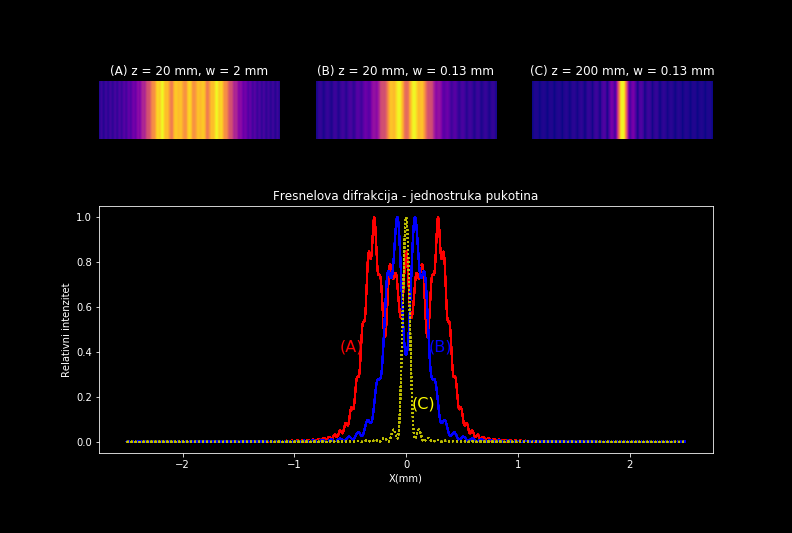
b) Difrakcija na jednostrukoj pukotini¶
Relativna veličina pukotine, difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju difrakcije na jednostrukoj pukotini. Talasna dužina svjetlosti je 632 nm. Vrijednosti širine pukotine i udaljenosti zaslona od otovora su prikazani na slici.
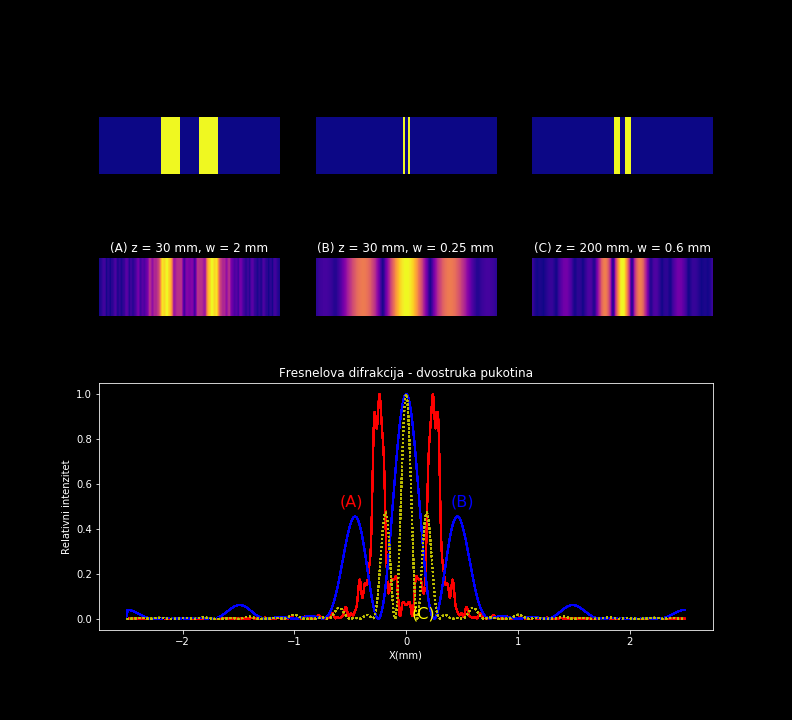
c) Difrakcija na dvostrukoj pukotini¶
Relativna veličina pukotine, difrakciona slika i relativni intenzitet zračenja na zaslonu u slučaju difrakcije na dvostrukoj pukotini. Talasna dužina svjetlosti je 632 nm. Vrijednosti polovine širine svake od pukotina i udaljenosti zaslona od otovora su prikazani na slici.
4. Zaključak¶
Brza Fourierova transformacija predstavlja vrlo važan i koristan matematički aparat koji omogućava efikasnu i jednostavnu analizu mnogih komplikovanih problema. Važnost Foruierove transformacije je od nemjerljivog značaja kako u obradi digitalnog signala (slike, zvuka), ali i u rješavanju složenih integrala. U slučaju difrakcije svjetlosti, problem rješavanja složenih integrala je zamijenjen odgovarajućom Fourierovom transformacijom, koja se opet uz korištenje algoritma Brze Fourierove transformacije lako rješava korištenjem kompjutacione moći modernih računara.
Literatura¶
Computer simulation of Fresnel diffraction from rectangular apertures and obstacles using the Fresnel integrals approach, K.M. Abedin à , M.R. Islam, A.F.M.Y. Haider, Optics & Laser Technology 39 (2007) 237–246
"History And Overview Of Diffraction Philosophy Essay." All Answers Ltd. ukessays.com, November 2013. Web. 20 June 2018. https://www.ukessays.com/essays/philosophy/history-and-overview-of-diffraction-philosophy-essay.php?vref=1.
Principles of Optics - Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Max Born & Emil Wolf, Pergamon Press 1980
Abedin, K. M., Islam, M. R., & Haider, A. F. M. Y. (2007). Computer simulation of Fresnel diffraction from rectangular apertures and obstacles using the Fresnel integrals approach. Optics and Laser Technology, 39(2), 237-246
An algorithm for the machine calculation of complex Fourier series, James W. Cooley and John W. Tukey, Math. Comp. 19 (1965), 297-301
Weisstein, Eric W. "Fast Fourier Transform." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FastFourierTransform.html
A Student's Guide to Fourier Transforms: With Applications in Physics and Engineering, J. F. James, Cambridge University Press; 2 edition (February 10, 2003)
Computer - simulated Fresnel diffraction using the Fourier transform, Seymour Trester, Computing in Science and Engineering 1(5):77 - 83, October 1999.
Understanding the FFT Algorithm, Pythonic Perambulations (web page)
A Taste of Python - Discrete and Fast Fourier Transforms, M. R. Muqri et. al., 122nd ASEE Anual Conference&Expostion, Seattle WA, June 2015.
Dodatak¶
Svi kodovi korišteni u generiranju gornjih slika iz poglavlja Rezultati moguće je pogledati na GitHub repozitoriju https://github.com/RifatO/Python. Za pisanje izvještaja korišten je Jupyter Notebook koji se može skinuti u istom direktoriju. Moguće je sve fajlove pogledati i na linkovima: