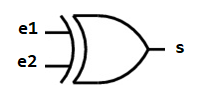© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.
Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.
Portes logiques et expressions booléennes
Activité sur les booléens n°1
Sommaire¶
1. Portes logiques et booléens
2. Circuits combinatoires
3. Complément : un outil
1. Portes logiques et booléens
Le codage d'une information ou sa circulation se font à l'aide de courant électrique.
Deux tensions sont possibles : 1 (haute) et 0 (basse), qui correspondent respectivement aux valeurs booléennes True et False.
Une porte logique reçoit un ou plusieurs signaux en entrée et renvoie un signal en sortie selon une règle préétablie.
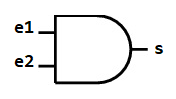
1.1. Dresser la table de vérité d'une porte logique consiste à recenser les valeurs obtenues en sortie en fonction des valeurs reçues en entrée.
$\quad\;\;$Recopier et compléter la table de vérité de la porte logique "et" ci-dessous :
1.2. Exécuter la cellule Python suivante, puis modifier/compléter pour vérifier l'ensemble de la table de vérité réalisée en 1.1.
# Exécuter/modifier cette cellule
e1 = True
e2 = True
s = e1 and e2
s
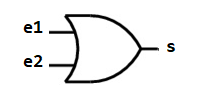
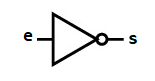
1.3. Dresser et compléter les tables de vérité des portes logiques "ou" et "non".
1.4. Effectuer des saisies Python pour vérifier ces tables de vérité.
# Effectuer ici les saisies Python
2. Circuits combinatoires
Les circuits combinatoires sont construits à partir de portes logiques élémentaires, qui sont en quelque sorte les briques élémentaires ces circuits.
2.1. On considère le circuit combinatoire noté Circuit1, donné ci-dessous. Dresser sa table de vérité.
$\quad\;\;$(on peut inclure des colonnes pour indiquer des valeurs intermédiaires)
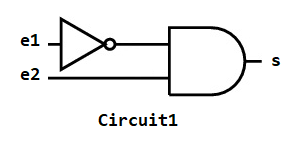
2.2. Écrire une fonction Python Circuit1, qui :
- reçoit en arguments deux booléens e1 et e2 ;
- renvoie le booléen s correspondant à la sortie de ce circuit.
#Écrire ici la fonction Circuit1
2.3. La fonction Python Table_verite donnée ci-dessous renvoie la table de vérité d'un circuit combinatoire donné par une fonction Python.
$\quad\;\;$Exécuter les cellules suivantes pour vérifier les résultats de la question 2.1.
from itertools import product
from inspect import signature
def Table_verite(fonction_booleenne):
"""
renvoie la table d'une fonction booléenne sous forme d'un dictionnaire
À chaque tuple des valeurs booléennes en entrée est associé la(les) sortie(s) correspondante(s)
"""
#récupération du nombre d'arguments de la fonction booleenne
nbre_arguments = len (signature(fonction_booleenne).parameters)
#initialisation de la table
Table={}
#remplissage de la table : à chaque séquence de booléens possible...
for liste_bool in product( *([[False,True] for j in range(nbre_arguments)] )):
#...on fait correspondre le résultat de la fonction booléenne
Table[liste_bool] = fonction_booleenne(*liste_bool)
#renvoie la table
return Table
#Exécuter cet appel à la fonction Table_verite
Table_verite(Circuit1)
2.4. Pour chacun des circuits combinatoires donnés ci-dessous:
- dresser sa table de vérité ;
- écrire une fonction Python correspondante ;
- vérifier la table de vérité à l'aide d'un appel à la fonction Python Table_verite
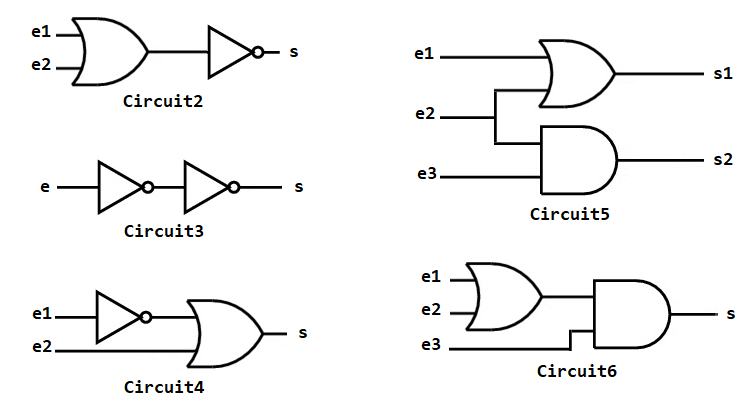
# Utiliser ces zones Python pour définir les fonctions et effectuer les appels à Table_verite
2.5. On considère le circuit combinatoire ci-dessous :
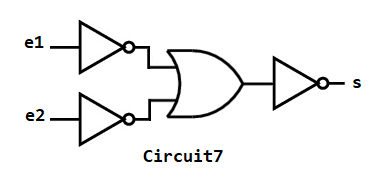 $\quad\;\;$a. Dresser sa table de vérité. Vérifier à l'aide de saisies Python.
$\quad\;\;$a. Dresser sa table de vérité. Vérifier à l'aide de saisies Python.$\quad\;\;$b. À quelle porte logique ce circuit correspond-t-il ?
$\quad\;\;$c. Proposer un circuit combinatoire qui réalise la fonction "ou" en utilisant uniquement des portes logiques élémentaires "et" et "non".
#Utiliser cette cellule pour la vérification de la question 2.5.a
2.6. On considère la porte " x-ou " ("x-or" , "ou exclusif") décrite ci-dessous :
$\quad\;\;$a. Dresser la table de vérité de cette porte " x-ou ".
$\quad\;\;$b. Proposer une construction de cette porte logique uniquement à l'aide de portes "et", "ou" et "non".
$\quad\;\;$c. La syntaxe Python $\;$^$\;$ permet de réaliser ce test logique entre deux booléens.
$\quad\quad\;$ Retrouver les résultats de la question 2.6.a à l'aide de saisies Python.
#Utiliser cette cellule pour la question 2.6.c

3. Complément : un outil
Dresser directement la table de vérité d'une expression sous forme str.
La fonction Table_description donnée ci-dessous permet d'obtenir la table de vérité d'une expression booléenne donnée directement sous forme de chaîne de caractère. Un exemple d'utilisation est fourni.
Attention : Pour éviter les bugs à la conversion, utiliser de préférence des variables nommées e1,e2,...
from itertools import product
def Table_description(liste_variables,operation_booleenne):
"""
Fonction qui renvoie la table de vérité sous forme d'un dictionnaire
liste_variables = ["e1","e2",...] liste des noms de variables utilisés
operation_booleene = "chaine de caractère (str) décrivant l'opération booléenne considérée"
"""
try:
#remplacement dans la chaîne de caractère des noms de variable par la syntaxe qui donnera la valeur de la variable
for k in range(len(liste_variables)):
operation_booleenne = operation_booleenne.replace(liste_variables[k],"valeur_var["+str(k)+"]")
#initialisation de la table
Table={}
#remplissage de la table : à chaque liste de booléens possible...
for valeur_var in product( *([[False,True] for j in range(len(liste_variables))] )):
#...on fait correspondre le résultat de la fonction booléenne
Table[valeur_var] = eval( operation_booleenne )
#renvoie la table
return Table
except:
return "saisie invalide"
# Exemple : Les variables se nomment e1,e2,e3 et l'expression évaluée est (e1 or e2) and e3
Table_description( ["e1","e2","e3"] , "(e1 or e2) and e3" )
© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.