
© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.
Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.
Algorithme de Brouncker pour le calcul de ln(2)¶
Le but de l'activité est d'obtenir une valeur approchée de $ln(2)$ à l'aide de l'algorithme de Brouncker, qui est basé sur une méthode géométrique.
1. Construction géométrique¶
On considère la fonction $h$ définie sur $\mathbb{R}^* $ par $h(x)=\frac{1}{x}$.
1.1. Démontrer que $ln(2)$ est l'aire de la zone délimitée par l'axe des abscisses, la courbe de la fonction $h$ et les droites d'équations $x=1$ et $x=2$. On cherche donc à donner une estimation de cette aire.
La figure dynamique suivante permet de visualiser la construction géométrique mise en œuvre.
Pour faire apparaître et activer l'animation, sélectionner la cellule ci-dessous et valider avec SHIFT+Entrée.
#Sélectionner cette zone puis SHIFT+ENTREE
from IPython.display import HTML ; HTML("""<iframe scrolling="no" title="Brouncker" src="https://www.geogebra.org/material/iframe/id/qk3xgkmr/width/806/height/586/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="806px" height="586px" style="border:0px;"> </iframe>""")
On "empile" successivement des rectangles sous la courbe de $h$ de la façon suivante :
- Le premier rectangle est construit sur l'axe des abscisses, entre les abscisses $1$ et $2$, et de hauteur maximale sous la courbe de $h$ ;
- À chaque étape, on introduit les milieux des abscisses utilisées à l'étape précédente, et on construit à partir de ces abscisses et des précédentes des rectangles situés au dessus des précédents, de hauteurs maximales sous la courbe de $h$.
Au vu de la figure, on admettra que les sommes des aires des rectangles ainsi successivement construits ont pour limite l'aire de la zone que l'on cherche à calculer.
Pour la suite, on utilisera les notations introduites sur les figures fournies.
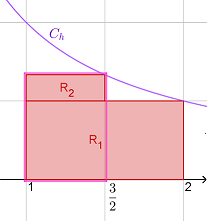
1.2. a. Calculer $Aire(R_1)$.
$\quad\;$ b. En raisonnant par soustraction, justifier que $Aire(R_2)=\frac{1}{3}-\frac{1}{4}$
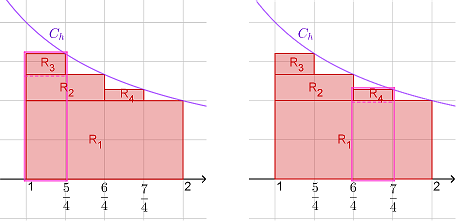
1.3. En raisonnant par soustraction, justifier que $Aire(R_3)=\frac{1}{5}-\frac{1}{6}$ puis que $Aire(R_4)=\frac{1}{7}-\frac{1}{8}$.
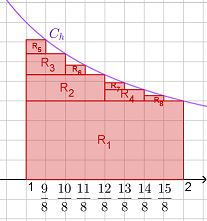
1.4 Donner les valeurs de $Aire(R_5)$, $Aire(R_6)$, $Aire(R_7)$ et $Aire(R_8)$.
2. Implémentation de l'algorithme de Brouncker¶
2.1. Soit $k\in\mathbb{N}^*$. En réduisant au même dénominateur, exprimer $\frac{1}{2k-1}-\frac{1}{2k}$ sous forme d'une fraction.
2.2. Justifier que la somme des $8$ rectangles $R_k$ précédemment construits, pour $1\leq k \leq 8$, vaut $ \sum\limits_{k=1}^8{\frac{1}{(2k-1)\times(2k)}} =\frac{1}{1\times2}+\frac{1}{3\times4}+...+\frac{1}{15\times16}$.
2.3. Écrire une fonction Python Brouncker qui permet de calculer cette somme.
$\quad\;$On pourra incrémenter un accumulateur S dans une boucle pour additionner, l'une après l'autre, les aires de ces rectangles.
# Écrire ici la fonction Brouncker qui renvoie la somme des 8 rectangles
# Écrire ici l'appel à la fonction Brouncker
On admet maintenant que la somme $ \sum\limits_{k=1}^n{\frac{1}{(2k-1)\times(2k)}} =\frac{1}{1\times2}+\frac{1}{3\times4}+...+\frac{1}{(2n-1)\times(2n)}$ a pour limite $ln(2)$ quand $n$ tend vers $+\infty$.
2.4. Adapter la fonction Brouncker précédente pour qu'elle reçoive $n$ en argument et permette de calculer cette somme.
# Écrire ici la fonction Brouncker qui renvoie la somme des n rectangles
2.5. Effectuer une saisie pour obtenir une valeur approchée de $ln(2)$ obtenue par la méthode de Brouncker avec 100 rectangles.
# Écrire ici l'appel à la fonction Brouncker
3. Recherche de la précision de la méthode¶
Dans la partie précédente, on a défini une suite $(u_n)_{n \geq 1}$ définie par $ u_n=\sum\limits_{k=1}^n{\frac{1}{(2k-1)\times(2k)}} =\frac{1}{1\times2}+\frac{1}{3\times4}+...+\frac{1}{(2n-1)\times(2n)}$ en considérant une somme d'aires de rectangles construits sous la courbe de $h$
On admet dans cette partie qu'en considérant des rectangles construits au dessus de la courbe de $h$, on peut définir une suite $(v_n)_{n \geq 1}$ définie par $ v_n=1-\sum\limits_{k=1}^n{\frac{1}{(2k)\times(2k+1)}} =1-\frac{1}{2\times3}-\frac{1}{4\times5}+...+\frac{1}{(2n)\times(2n+1)}$ qui vérifie $\lim\limits_{n \to +\infty}{v_n}=ln(2)$.
La figure dynamique suivante permet de visualiser la construction géométrique mise en œuvre.
Pour faire apparaître et activer l'animation, sélectionner la cellule ci-dessous et valider avec SHIFT+Entrée.
#Sélectionner cette zone puis SHIFT+ENTREE
from IPython.display import HTML ; HTML("""<iframe scrolling="no" title="Brouncker2" src="https://www.geogebra.org/material/iframe/id/d5kdhemy/width/736/height/579/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="736px" height="579px" style="border:0px;"> </iframe>""")
On admettra que :
- $\lim\limits_{n \to +\infty}{u_n}=\lim\limits_{n \to +\infty}{v_n}=ln(2)$
- Pour tout $n \geq 1$, on a $u_n \leq ln(2) \leq v_n$
On fixe $m>0$.
Ainsi, si $n$ vérifie $v_n - u_n \leq m$, alors $u_n$ et $v_n$ fournissent un encadrement de $ln(2)$ d'amplitude inférieure à $m$.
3.1. Reprendre la fonction Python Brouncker écrite dans la partie 2 et modifier cette fonction de telle sorte que :
- la fonction reçoit $m$ en argument
- dans la boucle on calcule à la fois $u_n$ et $v_n$
- la boucle s'interrompt dès que $v_n - u_n \leq m$
- la fonction renvoie les valeurs $u_n$ et $v_n$ finales
Aide : On utilisera une boucle while, et on introduira une variable $T$ pour le calcul des termes de $v_n$.
# Écrire ici la fonction Brouncker modifiée
3.2. À l'aide de la fonction obtenue à la question précédente, obtenir un encadrement de $ln(2)$ d'amplitude inférieure à $10^{-6}$.
# Effectuer ici l'appel à la fonction
3.3. La syntaxe from math import log permet d'utiliser la fonction Python log qui correspond à la fonction mathématique $ln$.
$\quad\;\;$Effectuer la saisie nécessaire pour calculer $ln(2)$, et vérifier la cohérence de l'encadrement obtenu à la question précédente.
# Écrire ici les saisies nécessaires pour calculer le logarithme népérien de 2

© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.