Using Python to solve Regexp CrossWord Puzzles¶
Have a look at the amazing https://regexcrossword.com/ website.
I played during about two hours, and could manually solve almost all problems, quite easily for most of them. But then I got stucked on this one.
Soooooo. I want to use Python3 regular expressions and try to solve any such cross-word puzzles.
Warning: This notebook will not explain the concept and syntax of regular expressions, go read on about it on Wikipedia or in a good book. The Python documentation gives a nice introduction here.
- Author: Lilian Besson (@Naereen) ;
- License: MIT License ;
- Date: 28-02-2021.
Representation of a problem¶
Here is a screenshot from the game webpage.
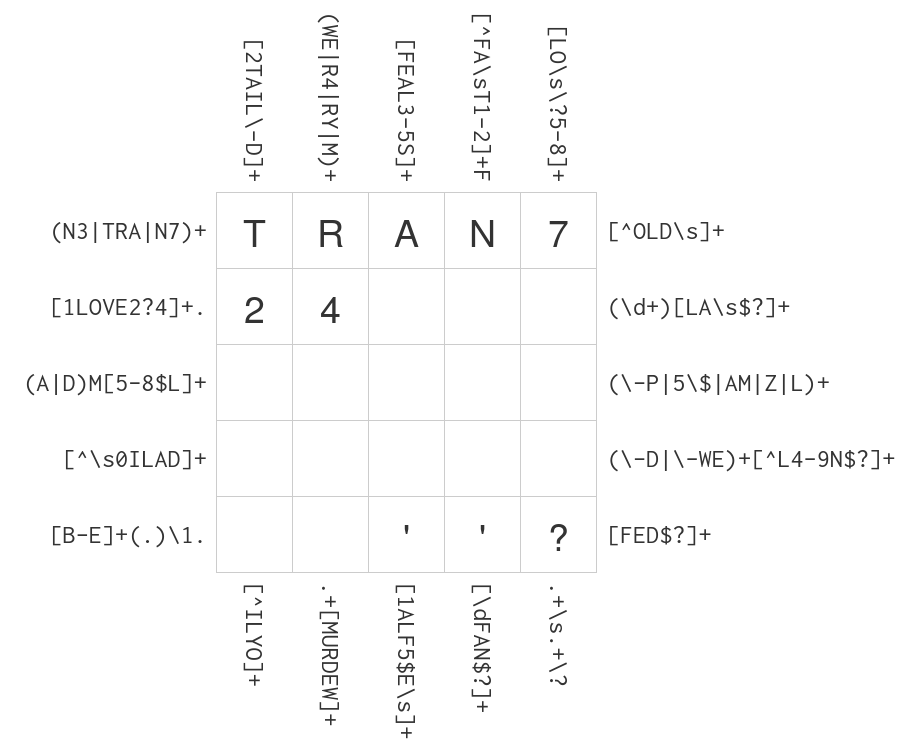
As you can see, an instance of this game is determined by its rectangular size, let's denote it $(m, n)$, so here there are $m=5$ lines and $n=5$ columns.
I'll also use this easy problem:

Let's define both, in a small dictionnary containing two to four lists of regexps.
Easy problem of size $(2,2)$ with four constraints¶
problem1 = {
"left_lines": [
r"HE|LL|O+", # HE|LL|O+ line 1
r"[PLEASE]+", # [PLEASE]+ line 2
],
"right_lines": None,
"top_columns": [
r"[^SPEAK]+", # [^SPEAK]+ column 1
r"EP|IP|EF", # EP|IP|EF column 2
],
"bottom_columns": None,
}
The keys "right_lines" and "bottom_columns" can be empty, as for easier problems there are no constraints on the right and bottom.
Each line and column (but not each square) contains a regular expression, on a common alphabet of letters and symbols.
Let's write $\Sigma$ this alphabet, which in the most general case is $\Sigma=\{$ A, B, ..., Z, 0, ..., 9, :, ?, ., $, -$\}$.
For the first beginner problem, the alphabet can be shorten:
alphabet1 = {
'H', 'E', 'L', 'O',
'P', 'L', 'E', 'A', 'S', 'E',
'S', 'P', 'E', 'A', 'K',
'E', 'P', 'I', 'P', 'I', 'F',
}
print(f"alphabet1 = \n{sorted(alphabet1)}")
alphabet1 = ['A', 'E', 'F', 'H', 'I', 'K', 'L', 'O', 'P', 'S']
Difficult problem of size $(5,5)$ with 20 constraints¶
Defining the second problem is just a question of more copy-pasting:
problem2 = {
"left_lines": [
r"(N3|TRA|N7)+", # left line 1
r"[1LOVE2?4]+.", # left line 2
r"(A|D)M[5-8$L]+", # left line 3
r"[^\s0ILAD]+", # left line 4
r"[B-E]+(.)\1.", # left line 5
],
"right_lines": [
r"[^OLD\s]+", # right line 1
r"(\d+)[LA\s$?]+", # right line 2
r"(\-P|5\$|AM|Z|L)+", # right line 3
r"(\-D|\-WE)+[^L4-9N$?]+", # right line 4
r"[FED$?]+", # right line 5
],
"top_columns": [
r"[2TAIL\-D]+", # top column 1
r"(WE|R4|RY|M)+", # top column 2
r"[FEAL3-5S]+", # top column 3
r"[^FA\sT1-2]+F", # top column 4
r"[LO\s\?5-8]+", # top column 5
],
"bottom_columns": [
r"[^ILYO]+", # top column 1
r".+[MURDEW]+", # top column 2
r"[1ALF5$E\s]+", # top column 3
r"[\dFAN$?]+", # top column 4
r".+\s.+\?", # top column 5
],
}
And its alphabet:
import string
alphabet2 = set(string.digits) \
| set(string.ascii_uppercase) \
| { ':', '?', '.', '$', '-' }
print(f"alphabet2 = \n{sorted(alphabet2)}")
alphabet2 = ['$', '-', '.', '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', ':', '?', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
An intermediate problem of size $(3,3)$ with 12 constraints¶
Defining the third problem is just a question of more copy-pasting:
problem3 = {
"left_lines": [
r"[ONE]*[SKA]", # left line 1
r".*(RE|ER)", # left line 2
r"A+[TUB]*", # left line 3
],
"right_lines": [
r".*(O|S)*", # right line 1
r"[^GOA]*", # right line 2
r"[STUPA]+", # right line 3
],
"top_columns": [
r".*[GAF]*", # top column 1
r"(P|ET|O|TEA)*", # top column 2
r"[RUSH]+", # top column 3
],
"bottom_columns": [
r"(NF|FA|A|FN)+", # top column 1
r".*(A|E|I).*", # top column 2
r"[SUPER]*", # top column 3
],
}
And its alphabet:
alphabet3 = {
'O', 'N', 'E', 'S', 'K', 'A',
'R', 'E', 'E', 'R',
'A', 'T', 'U', 'B',
'O', 'S',
'G', 'O', 'A',
'S', 'T', 'U', 'P', 'A',
'G', 'A', 'F',
'P', 'E', 'T', 'O', 'T', 'E', 'A',
'R', 'U', 'S', 'H',
'N', 'F', 'F', 'A', 'A', 'F', 'N',
'A', 'E', 'I',
'S', 'U', 'P', 'E', 'R',
}
print(f"alphabet3 = \n{sorted(alphabet3)}")
alphabet3 = ['A', 'B', 'E', 'F', 'G', 'H', 'I', 'K', 'N', 'O', 'P', 'R', 'S', 'T', 'U']
A few useful functions¶
Let's first extract the dimension of a problem:
def dimension_problem(problem):
m = len(problem['left_lines'])
if problem['right_lines'] is not None:
assert m == len(problem['right_lines'])
n = len(problem['top_columns'])
if problem['bottom_columns'] is not None:
assert n == len(problem['bottom_columns'])
return (m, n)
problem1
{'left_lines': ['HE|LL|O+', '[PLEASE]+'],
'right_lines': None,
'top_columns': ['[^SPEAK]+', 'EP|IP|EF'],
'bottom_columns': None}
dimension_problem(problem1)
(2, 2)
Now let's write a representation of a grid, a solution (or partial solution) of a problem:
___ = "_" # represents an empty answer, as _ is not in the alphabet
grid1_partial = [
[ 'H', ___ ],
[ ___, 'P' ],
]
grid1_solution = [
[ 'H', 'E' ],
[ 'L', 'P' ],
]
As well as a few complete grids which are NOT solutions
grid1_wrong1 = [
[ 'H', 'E' ],
[ 'L', 'F' ],
]
grid1_wrong2 = [
[ 'H', 'E' ],
[ 'E', 'P' ],
]
grid1_wrong3 = [
[ 'H', 'E' ],
[ 'O', 'F' ],
]
grid1_wrong4 = [
[ 'O', 'E' ],
[ 'O', 'F' ],
]
We also write these short functions to extract the $i$-th line or $j$-th column:
def nth_line(grid, line):
return "".join(grid[line])
def nth_column(grid, column):
return "".join(grid[line][column] for line in range(len(grid)))
[ nth_line(grid1_solution, line) for line in range(len(grid1_solution)) ]
['HE', 'LP']
[ nth_column(grid1_solution, column) for column in range(len(grid1_solution[0])) ]
['HL', 'EP']
A partial solution for the intermediate problem:
___ = "_" # represents an empty answer, as _ is not in the alphabet
grid3_solution = [
[ 'N', 'O', 'S' ],
[ 'F', 'E', 'R' ],
[ 'A', 'T', 'U' ],
]
And a partial solution for the harder problem:
___ = "_" # represents an empty answer, as _ is not in the alphabet
grid2_partial = [
[ 'T', 'R', 'A', 'N', '7' ],
[ '2', '4', ___, ___, ' ' ],
[ 'A', ___, ___, ___, ___ ],
[ '-', ___, ___, ___, ___ ],
[ 'D', ___, ___, ___, '?' ],
]
Let's extract the dimension of a grid, just to check it:
def dimension_grid(grid):
m = len(grid)
n = len(grid[0])
assert all(n == len(grid[i]) for i in range(1, m))
return (m, n)
print(f"Grid grid1_partial has dimension: {dimension_grid(grid1_partial)}")
print(f"Grid grid1_solution has dimension: {dimension_grid(grid1_solution)}")
Grid grid1_partial has dimension: (2, 2) Grid grid1_solution has dimension: (2, 2)
print(f"Grid grid2_partial has dimension: {dimension_grid(grid2_partial)}")
Grid grid2_partial has dimension: (5, 5)
def check_dimensions(problem, grid):
return dimension_problem(problem) == dimension_grid(grid)
assert check_dimensions(problem1, grid1_partial)
assert check_dimensions(problem1, grid1_solution)
assert not check_dimensions(problem2, grid1_partial)
assert check_dimensions(problem2, grid2_partial)
assert not check_dimensions(problem1, grid2_partial)
Two more checks¶
We also have to check if a word is in an alphabet:
def check_alphabet(alphabet, word, debug=True):
result = True
for i, letter in enumerate(word):
new_result = letter in alphabet
if debug and result and not new_result:
print(f"The word {repr(word)} is not in alphabet {repr(alphabet)}, as its #{i}th letter {letter} is not present.")
result = result and new_result
return result
assert check_alphabet(alphabet1, 'H' 'E') # concatenate the strings
assert check_alphabet(alphabet1, 'H' 'E')
assert check_alphabet(alphabet1, 'L' 'P')
assert check_alphabet(alphabet1, 'H' 'L')
assert check_alphabet(alphabet1, 'E' 'P')
assert check_alphabet(alphabet2, "TRAN7")
And also check that a word matches a regexp:
import re
As the documentation explains it:
but using
prog = re.compile(regepx)and saving the resulting regular expression objectprogfor reuse is more efficient when the expression will be used several times in a single program.
I don't want to have to think about compiling a regexp before using it, so... I'm gonna memoize them!
memory_of_compiled_regexps = dict()
Now we are ready to write our "smart" match function:
def match(regexp, word, debug=True):
global memory_of_compiled_regexps
if regexp not in memory_of_compiled_regexps:
prog = re.compile(regexp)
memory_of_compiled_regexps[regexp] = prog
print(f"For the first time seeing this regexp {repr(regexp)}, compiling it and storing in memory_of_compiled_regexps, now of size {len(memory_of_compiled_regexps)}.")
else:
prog = memory_of_compiled_regexps[regexp]
result = re.fullmatch(regexp, word)
result = prog.fullmatch(word)
entire_match = result is not None
# entire_match = result.group(0) == word
if debug:
if entire_match:
print(f"The word {repr(word)} is matched by {repr(regexp)}")
else:
print(f"The word {repr(word)} is NOT matched by {repr(regexp)}")
return entire_match
Let's compare the time of the first match and next ones:
%%time
match(r"(N3|TRA|N7)+", "TRAN7")
For the first time seeing this regexp '(N3|TRA|N7)+', compiling it and storing in memory_of_compiled_regexps, now of size 1. The word 'TRAN7' is matched by '(N3|TRA|N7)+' CPU times: user 238 µs, sys: 0 ns, total: 238 µs Wall time: 173 µs
True
%%time
match(r"(N3|TRA|N7)+", "TRAN8")
The word 'TRAN8' is NOT matched by '(N3|TRA|N7)+' CPU times: user 176 µs, sys: 71 µs, total: 247 µs Wall time: 169 µs
False
Well of course it's not different for tiny test like this.
match(r"(N3|TRA|N7)+", "")
match(r"(N3|TRA|N7)+", "TRA")
That should be enough to start the first "easy" task.
%timeit match(r"(N3|TRA|N7)+", "TRA", debug=False)
%timeit re.fullmatch(r"(N3|TRA|N7)+", "TRA")
1.14 µs ± 15.9 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) 603 ns ± 7.87 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
We can see that our "memoization trick" indeed helped to speed-up the time required to check a regexp, by about a factor 2, even for very small tests like this.
First easy task: check that a line/column word validate its contraints¶
Given a problem $P$ of dimension $(m, n)$, its alphabet $\Sigma$, a position $i \in [| 0, m-1 |]$ of a line or $j \times [|0, n-1 |]$ of a column, and a word $w \in \Sigma^k$ (with $k=m$ for line or $k=n$ for column), I want to write a function that checks the validity of each (left/right) line, or (top/bottom) constraints.
To ease debugging, and in the goal of using this Python program to improve my skills in solving such puzzles, I don't want this function to just reply True or False, but to also print for each constraints if it is satisfied or not.
Bonus: for each regexp contraint, highlight the parts which corresponded to each letter of the word?
For lines¶
We are ready to check the one or two constraints of a line. The same function will be written for columns, just below.
def check_line(problem, alphabet, word, position, debug=True, early=False):
if not check_alphabet(alphabet, word, debug=debug):
return False
m, n = dimension_problem(problem)
if len(word) != n:
if debug:
print(f"Word {repr(word)} does not have correct size n = {n} for lines")
return False
assert 0 <= position < m
constraints = []
if "left_lines" in problem and problem["left_lines"] is not None:
constraints += [ problem["left_lines"][position] ]
if "right_lines" in problem and problem["right_lines"] is not None:
constraints += [ problem["right_lines"][position] ]
# okay we have one or two constraint for this line,
assert len(constraints) in {1, 2}
# let's check them!
result = True
for cnb, constraint in enumerate(constraints):
if debug:
print(f"For line constraint #{cnb} {repr(constraint)}:")
new_result = match(constraint, word, debug=debug)
if early and not new_result: return False
result = result and new_result
return result
Let's try it!
problem1, alphabet1, grid1_solution
({'left_lines': ['HE|LL|O+', '[PLEASE]+'],
'right_lines': None,
'top_columns': ['[^SPEAK]+', 'EP|IP|EF'],
'bottom_columns': None},
{'A', 'E', 'F', 'H', 'I', 'K', 'L', 'O', 'P', 'S'},
[['H', 'E'], ['L', 'P']])
n, m = dimension_problem(problem1)
for line in range(n):
word = nth_line(grid1_solution, line)
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem1, alphabet1, word, line)
- For line number 0, checking word 'HE': For line constraint #0 'HE|LL|O+': For the first time seeing this regexp 'HE|LL|O+', compiling it and storing in memory_of_compiled_regexps, now of size 2. The word 'HE' is matched by 'HE|LL|O+' - For line number 1, checking word 'LP': For line constraint #0 '[PLEASE]+': For the first time seeing this regexp '[PLEASE]+', compiling it and storing in memory_of_compiled_regexps, now of size 3. The word 'LP' is matched by '[PLEASE]+'
n, m = dimension_problem(problem1)
fake_words = ["OK", "HEY", "NOT", "HELL", "N", "", "HU", "OO", "EA"]
for word in fake_words:
print(f"# For word {repr(word)}:")
for line in range(n):
result = check_line(problem1, alphabet1, word, line)
print(f" => {result}")
# For word 'OK':
For line constraint #0 'HE|LL|O+':
The word 'OK' is NOT matched by 'HE|LL|O+'
=> False
For line constraint #0 '[PLEASE]+':
The word 'OK' is NOT matched by '[PLEASE]+'
=> False
# For word 'HEY':
The word 'HEY' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #2th letter Y is not present.
=> False
The word 'HEY' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #2th letter Y is not present.
=> False
# For word 'NOT':
The word 'NOT' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
The word 'NOT' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
# For word 'HELL':
Word 'HELL' does not have correct size n = 2 for lines
=> False
Word 'HELL' does not have correct size n = 2 for lines
=> False
# For word 'N':
The word 'N' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
The word 'N' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
# For word '':
Word '' does not have correct size n = 2 for lines
=> False
Word '' does not have correct size n = 2 for lines
=> False
# For word 'HU':
The word 'HU' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter U is not present.
=> False
The word 'HU' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter U is not present.
=> False
# For word 'OO':
For line constraint #0 'HE|LL|O+':
The word 'OO' is matched by 'HE|LL|O+'
=> True
For line constraint #0 '[PLEASE]+':
The word 'OO' is NOT matched by '[PLEASE]+'
=> False
# For word 'EA':
For line constraint #0 'HE|LL|O+':
The word 'EA' is NOT matched by 'HE|LL|O+'
=> False
For line constraint #0 '[PLEASE]+':
The word 'EA' is matched by '[PLEASE]+'
=> True
That was long, but it works fine!
n, m = dimension_problem(problem2)
for line in [0]:
word = nth_line(grid2_partial, line)
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem2, alphabet2, word, line)
print(f" => {result}")
- For line number 0, checking word 'TRAN7': For line constraint #0 '(N3|TRA|N7)+': The word 'TRAN7' is matched by '(N3|TRA|N7)+' For line constraint #1 '[^OLD\\s]+': For the first time seeing this regexp '[^OLD\\s]+', compiling it and storing in memory_of_compiled_regexps, now of size 4. The word 'TRAN7' is matched by '[^OLD\\s]+' => True
n, m = dimension_problem(problem2)
fake_words = [
"TRAN8", "N2TRA", # violate first constraint
"N3N3N7", "N3N3", "TRA9", # smaller or bigger dimension
"O L D", "TRA ", # violate second contraint
]
for word in fake_words:
for line in [0]:
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_line(problem2, alphabet2, word, line)
print(f" => {result}")
- For line number 0, checking word 'TRAN8':
For line constraint #0 '(N3|TRA|N7)+':
The word 'TRAN8' is NOT matched by '(N3|TRA|N7)+'
For line constraint #1 '[^OLD\\s]+':
The word 'TRAN8' is matched by '[^OLD\\s]+'
=> False
- For line number 0, checking word 'N2TRA':
For line constraint #0 '(N3|TRA|N7)+':
The word 'N2TRA' is NOT matched by '(N3|TRA|N7)+'
For line constraint #1 '[^OLD\\s]+':
The word 'N2TRA' is matched by '[^OLD\\s]+'
=> False
- For line number 0, checking word 'N3N3N7':
Word 'N3N3N7' does not have correct size n = 5 for lines
=> False
- For line number 0, checking word 'N3N3':
Word 'N3N3' does not have correct size n = 5 for lines
=> False
- For line number 0, checking word 'TRA9':
Word 'TRA9' does not have correct size n = 5 for lines
=> False
- For line number 0, checking word 'O L D':
The word 'O L D' is not in alphabet {'Z', 'E', 'I', 'V', 'R', 'A', 'F', 'D', 'Q', '3', 'Y', 'L', '4', 'W', '$', '5', 'M', 'B', 'N', '2', '8', '1', 'T', 'X', 'H', '-', 'S', '?', 'G', '9', 'U', 'P', '7', 'O', '.', 'C', 'J', 'K', '0', '6', ':'}, as its #1th letter is not present.
=> False
- For line number 0, checking word 'TRA ':
The word 'TRA ' is not in alphabet {'Z', 'E', 'I', 'V', 'R', 'A', 'F', 'D', 'Q', '3', 'Y', 'L', '4', 'W', '$', '5', 'M', 'B', 'N', '2', '8', '1', 'T', 'X', 'H', '-', 'S', '?', 'G', '9', 'U', 'P', '7', 'O', '.', 'C', 'J', 'K', '0', '6', ':'}, as its #3th letter is not present.
=> False
For columns¶
We are ready to check the one or two constraints of a line. The same function will be written for columns, just below.
def check_column(problem, alphabet, word, position, debug=True, early=False):
if not check_alphabet(alphabet, word, debug=debug):
return False
m, n = dimension_problem(problem)
if len(word) != m:
if debug:
print(f"Word {repr(word)} does not have correct size n = {n} for columns")
return False
assert 0 <= position < n
constraints = []
if "top_columns" in problem and problem["top_columns"] is not None:
constraints += [ problem["top_columns"][position] ]
if "bottom_columns" in problem and problem["bottom_columns"] is not None:
constraints += [ problem["bottom_columns"][position] ]
# okay we have one or two constraint for this column,
assert len(constraints) in {1, 2}
# let's check them!
result = True
for cnb, constraint in enumerate(constraints):
if debug:
print(f"For column constraint #{cnb} {repr(constraint)}:")
new_result = match(constraint, word, debug=debug)
if early and not new_result: return False
result = result and new_result
return result
Let's try it!
problem1, alphabet1, grid1_solution
({'left_lines': ['HE|LL|O+', '[PLEASE]+'],
'right_lines': None,
'top_columns': ['[^SPEAK]+', 'EP|IP|EF'],
'bottom_columns': None},
{'A', 'E', 'F', 'H', 'I', 'K', 'L', 'O', 'P', 'S'},
[['H', 'E'], ['L', 'P']])
n, m = dimension_problem(problem1)
for column in range(m):
word = nth_column(grid1_solution, column)
print(f"- For column number {column}, checking word {repr(word)}:")
result = check_column(problem1, alphabet1, word, column)
- For column number 0, checking word 'HL': For column constraint #0 '[^SPEAK]+': For the first time seeing this regexp '[^SPEAK]+', compiling it and storing in memory_of_compiled_regexps, now of size 5. The word 'HL' is matched by '[^SPEAK]+' - For column number 1, checking word 'EP': For column constraint #0 'EP|IP|EF': For the first time seeing this regexp 'EP|IP|EF', compiling it and storing in memory_of_compiled_regexps, now of size 6. The word 'EP' is matched by 'EP|IP|EF'
n, m = dimension_problem(problem1)
fake_words = ["OK", "HEY", "NOT", "HELL", "N", "", "HU", "OO", "EA"]
for word in fake_words:
print(f"# For word {repr(word)}:")
for column in range(m):
result = check_column(problem1, alphabet1, word, column)
print(f" => {result}")
# For word 'OK':
For column constraint #0 '[^SPEAK]+':
The word 'OK' is NOT matched by '[^SPEAK]+'
=> False
For column constraint #0 'EP|IP|EF':
The word 'OK' is NOT matched by 'EP|IP|EF'
=> False
# For word 'HEY':
The word 'HEY' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #2th letter Y is not present.
=> False
The word 'HEY' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #2th letter Y is not present.
=> False
# For word 'NOT':
The word 'NOT' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
The word 'NOT' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
# For word 'HELL':
Word 'HELL' does not have correct size n = 2 for columns
=> False
Word 'HELL' does not have correct size n = 2 for columns
=> False
# For word 'N':
The word 'N' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
The word 'N' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter N is not present.
=> False
# For word '':
Word '' does not have correct size n = 2 for columns
=> False
Word '' does not have correct size n = 2 for columns
=> False
# For word 'HU':
The word 'HU' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter U is not present.
=> False
The word 'HU' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter U is not present.
=> False
# For word 'OO':
For column constraint #0 '[^SPEAK]+':
The word 'OO' is matched by '[^SPEAK]+'
=> True
For column constraint #0 'EP|IP|EF':
The word 'OO' is NOT matched by 'EP|IP|EF'
=> False
# For word 'EA':
For column constraint #0 '[^SPEAK]+':
The word 'EA' is NOT matched by '[^SPEAK]+'
=> False
For column constraint #0 'EP|IP|EF':
The word 'EA' is NOT matched by 'EP|IP|EF'
=> False
That was long, but it works fine!
n, m = dimension_problem(problem2)
for column in [0]:
word = nth_column(grid2_partial, column)
print(f"- For column number {column}, checking word {repr(word)}:")
result = check_column(problem2, alphabet2, word, column)
print(f" => {result}")
- For column number 0, checking word 'T2A-D': For column constraint #0 '[2TAIL\\-D]+': For the first time seeing this regexp '[2TAIL\\-D]+', compiling it and storing in memory_of_compiled_regexps, now of size 7. The word 'T2A-D' is matched by '[2TAIL\\-D]+' For column constraint #1 '[^ILYO]+': For the first time seeing this regexp '[^ILYO]+', compiling it and storing in memory_of_compiled_regexps, now of size 8. The word 'T2A-D' is matched by '[^ILYO]+' => True
n, m = dimension_problem(problem2)
fake_words = [
"TRAN8", "N2TRA", # violate first constraint
"N3N3N7", "N3N3", "TRA9", # smaller or bigger dimension
"O L D", "TRA ", # violate second contraint
]
for word in fake_words:
for line in [0]:
print(f"- For line number {line}, checking word {repr(word)}:")
result = check_column(problem2, alphabet2, word, line)
print(f" => {result}")
- For line number 0, checking word 'TRAN8':
For column constraint #0 '[2TAIL\\-D]+':
The word 'TRAN8' is NOT matched by '[2TAIL\\-D]+'
For column constraint #1 '[^ILYO]+':
The word 'TRAN8' is matched by '[^ILYO]+'
=> False
- For line number 0, checking word 'N2TRA':
For column constraint #0 '[2TAIL\\-D]+':
The word 'N2TRA' is NOT matched by '[2TAIL\\-D]+'
For column constraint #1 '[^ILYO]+':
The word 'N2TRA' is matched by '[^ILYO]+'
=> False
- For line number 0, checking word 'N3N3N7':
Word 'N3N3N7' does not have correct size n = 5 for columns
=> False
- For line number 0, checking word 'N3N3':
Word 'N3N3' does not have correct size n = 5 for columns
=> False
- For line number 0, checking word 'TRA9':
Word 'TRA9' does not have correct size n = 5 for columns
=> False
- For line number 0, checking word 'O L D':
The word 'O L D' is not in alphabet {'Z', 'E', 'I', 'V', 'R', 'A', 'F', 'D', 'Q', '3', 'Y', 'L', '4', 'W', '$', '5', 'M', 'B', 'N', '2', '8', '1', 'T', 'X', 'H', '-', 'S', '?', 'G', '9', 'U', 'P', '7', 'O', '.', 'C', 'J', 'K', '0', '6', ':'}, as its #1th letter is not present.
=> False
- For line number 0, checking word 'TRA ':
The word 'TRA ' is not in alphabet {'Z', 'E', 'I', 'V', 'R', 'A', 'F', 'D', 'Q', '3', 'Y', 'L', '4', 'W', '$', '5', 'M', 'B', 'N', '2', '8', '1', 'T', 'X', 'H', '-', 'S', '?', 'G', '9', 'U', 'P', '7', 'O', '.', 'C', 'J', 'K', '0', '6', ':'}, as its #3th letter is not present.
=> False
Second easy task: check that a proposed grid is a valid solution¶
I think it's easy, as we just have to use $m$ times the check_line and $n$ times the check_column functions.
def check_grid(problem, alphabet, grid, debug=True, early=False):
m, n = dimension_problem(problem)
ok_lines = [False] * m
for line in range(m):
word = nth_line(grid, line)
ok_lines[line] = check_line(problem, alphabet, word, line, debug=debug, early=early)
ok_columns = [False] * n
for column in range(n):
word = nth_column(grid, column)
ok_columns[column] = check_column(problem, alphabet, word, column, debug=debug, early=early)
return all(ok_lines) and all(ok_columns)
Let's try it!
For the easy problem¶
For a partial grid, of course it's going to be invalid just because '_' is not in the alphabet $\Sigma$.
check_grid(problem1, alphabet1, grid1_partial)
The word 'H_' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter _ is not present.
The word '_P' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter _ is not present.
The word 'H_' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #1th letter _ is not present.
The word '_P' is not in alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}, as its #0th letter _ is not present.
False
For a complete grid, let's check that our solution is valid:
check_grid(problem1, alphabet1, grid1_solution)
For line constraint #0 'HE|LL|O+': The word 'HE' is matched by 'HE|LL|O+' For line constraint #0 '[PLEASE]+': The word 'LP' is matched by '[PLEASE]+' For column constraint #0 '[^SPEAK]+': The word 'HL' is matched by '[^SPEAK]+' For column constraint #0 'EP|IP|EF': The word 'EP' is matched by 'EP|IP|EF'
True
And let's also check that the few wrong solutions are indeed not valid:
check_grid(problem1, alphabet1, grid1_wrong1)
For line constraint #0 'HE|LL|O+': The word 'HE' is matched by 'HE|LL|O+' For line constraint #0 '[PLEASE]+': The word 'LF' is NOT matched by '[PLEASE]+' For column constraint #0 '[^SPEAK]+': The word 'HL' is matched by '[^SPEAK]+' For column constraint #0 'EP|IP|EF': The word 'EF' is matched by 'EP|IP|EF'
False
check_grid(problem1, alphabet1, grid1_wrong2)
For line constraint #0 'HE|LL|O+': The word 'HE' is matched by 'HE|LL|O+' For line constraint #0 '[PLEASE]+': The word 'EP' is matched by '[PLEASE]+' For column constraint #0 '[^SPEAK]+': The word 'HE' is NOT matched by '[^SPEAK]+' For column constraint #0 'EP|IP|EF': The word 'EP' is matched by 'EP|IP|EF'
False
check_grid(problem1, alphabet1, grid1_wrong3)
For line constraint #0 'HE|LL|O+': The word 'HE' is matched by 'HE|LL|O+' For line constraint #0 '[PLEASE]+': The word 'OF' is NOT matched by '[PLEASE]+' For column constraint #0 '[^SPEAK]+': The word 'HO' is matched by '[^SPEAK]+' For column constraint #0 'EP|IP|EF': The word 'EF' is matched by 'EP|IP|EF'
False
check_grid(problem1, alphabet1, grid1_wrong4)
For line constraint #0 'HE|LL|O+': The word 'OE' is NOT matched by 'HE|LL|O+' For line constraint #0 '[PLEASE]+': The word 'OF' is NOT matched by '[PLEASE]+' For column constraint #0 '[^SPEAK]+': The word 'OO' is matched by '[^SPEAK]+' For column constraint #0 'EP|IP|EF': The word 'EF' is matched by 'EP|IP|EF'
False
We can see that for each wrong grid, at least one of the contraint is violated!
That's pretty good!
check_grid(problem3, alphabet3, grid3_solution)
For line constraint #0 '[ONE]*[SKA]': For the first time seeing this regexp '[ONE]*[SKA]', compiling it and storing in memory_of_compiled_regexps, now of size 9. The word 'NOS' is matched by '[ONE]*[SKA]' For line constraint #1 '.*(O|S)*': For the first time seeing this regexp '.*(O|S)*', compiling it and storing in memory_of_compiled_regexps, now of size 10. The word 'NOS' is matched by '.*(O|S)*' For line constraint #0 '.*(RE|ER)': For the first time seeing this regexp '.*(RE|ER)', compiling it and storing in memory_of_compiled_regexps, now of size 11. The word 'FER' is matched by '.*(RE|ER)' For line constraint #1 '[^GOA]*': For the first time seeing this regexp '[^GOA]*', compiling it and storing in memory_of_compiled_regexps, now of size 12. The word 'FER' is matched by '[^GOA]*' For line constraint #0 'A+[TUB]*': For the first time seeing this regexp 'A+[TUB]*', compiling it and storing in memory_of_compiled_regexps, now of size 13. The word 'ATU' is matched by 'A+[TUB]*' For line constraint #1 '[STUPA]+': For the first time seeing this regexp '[STUPA]+', compiling it and storing in memory_of_compiled_regexps, now of size 14. The word 'ATU' is matched by '[STUPA]+' For column constraint #0 '.*[GAF]*': For the first time seeing this regexp '.*[GAF]*', compiling it and storing in memory_of_compiled_regexps, now of size 15. The word 'NFA' is matched by '.*[GAF]*' For column constraint #1 '(NF|FA|A|FN)+': For the first time seeing this regexp '(NF|FA|A|FN)+', compiling it and storing in memory_of_compiled_regexps, now of size 16. The word 'NFA' is matched by '(NF|FA|A|FN)+' For column constraint #0 '(P|ET|O|TEA)*': For the first time seeing this regexp '(P|ET|O|TEA)*', compiling it and storing in memory_of_compiled_regexps, now of size 17. The word 'OET' is matched by '(P|ET|O|TEA)*' For column constraint #1 '.*(A|E|I).*': For the first time seeing this regexp '.*(A|E|I).*', compiling it and storing in memory_of_compiled_regexps, now of size 18. The word 'OET' is matched by '.*(A|E|I).*' For column constraint #0 '[RUSH]+': For the first time seeing this regexp '[RUSH]+', compiling it and storing in memory_of_compiled_regexps, now of size 19. The word 'SRU' is matched by '[RUSH]+' For column constraint #1 '[SUPER]*': For the first time seeing this regexp '[SUPER]*', compiling it and storing in memory_of_compiled_regexps, now of size 20. The word 'SRU' is matched by '[SUPER]*'
True
For the hard problem¶
Well I don't have a solution yet, so I cannot check it!
Third easy task: generate all words of a given size in the alphabet¶
Using itertools.product and the alphabet defined above, it's going to be easy.
Note that I'll first try with a smaller alphabet, to check the result (for problem 1).
import itertools
def all_words_of_alphabet(alphabet, size):
yield from itertools.product(alphabet, repeat=size)
Just a quick check:
list(all_words_of_alphabet(['0', '1'], 3))
[('0', '0', '0'),
('0', '0', '1'),
('0', '1', '0'),
('0', '1', '1'),
('1', '0', '0'),
('1', '0', '1'),
('1', '1', '0'),
('1', '1', '1')]
The time and memory complexity of this function should be $\mathcal{O}(|\Sigma|^k)$ for words of size $k\in\mathbb{N}^*$.
alphabet0 = ['0', '1']
len_alphabet = len(alphabet0)
for k in [2, 3, 4, 5]:
print(f"Generating {len_alphabet**k} words of size = {k} takes about")
%timeit list(all_words_of_alphabet(alphabet0, k))
Generating 4 words of size = 2 takes about 754 ns ± 13.4 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) Generating 8 words of size = 3 takes about 923 ns ± 9.82 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) Generating 16 words of size = 4 takes about 1.38 µs ± 30.9 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each) Generating 32 words of size = 5 takes about 2.28 µs ± 44 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
%timeit list(all_words_of_alphabet(['0', '1', '2', '3'], 10))
117 ms ± 1.39 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
We can quickly check that even for the larger alphabet of size ~40, it's quite quick for small words of length $\leq 5$:
len_alphabet = len(alphabet1)
for k in [2, 3, 4, 5]:
print(f"Generating {len_alphabet**k} words of size = {k} takes about")
%timeit list(all_words_of_alphabet(alphabet1, k))
Generating 100 words of size = 2 takes about 6.27 µs ± 1.35 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each) Generating 1000 words of size = 3 takes about 45.9 µs ± 729 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each) Generating 10000 words of size = 4 takes about 519 µs ± 6.06 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each) Generating 100000 words of size = 5 takes about 8.36 ms ± 330 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
len_alphabet = len(alphabet2)
for k in [2, 3, 4, 5]:
print(f"Generating {len_alphabet**k} words of size = {k} takes about")
%timeit list(all_words_of_alphabet(alphabet2, k))
Generating 1681 words of size = 2 takes about 79.2 µs ± 990 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each) Generating 68921 words of size = 3 takes about 4.57 ms ± 51.2 µs per loop (mean ± std. dev. of 7 runs, 100 loops each) Generating 2825761 words of size = 4 takes about 230 ms ± 4.53 ms per loop (mean ± std. dev. of 7 runs, 1 loop each) Generating 115856201 words of size = 5 takes about 11.1 s ± 215 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Who, it takes 12 seconds to just generate all the possible words for the largest problem (which is just of size $(5,5)$)...
I'm afraid that my naive approach to solve the puzzle will be VERY slow...
Fourth easy task: generate all grids of a given size¶
def all_grids_of_alphabet(alphabet, lines, columns):
all_words = list(itertools.product(alphabet, repeat=columns))
all_words = [ "".join(words) for words in all_words ]
all_grids = itertools.product(all_words, repeat=lines)
for pre_tr_grid in all_grids:
tr_grid = [
[
pre_tr_grid[line][column]
for line in range(lines)
]
for column in range(columns)
]
yield tr_grid
for alphabet in ( ['0', '1'], ['T', 'A', 'C', 'G'] ):
for (n, m) in [ (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (3, 2), (2, 3) ]:
assert len(list(all_grids_of_alphabet(alphabet, n, m))) == len(alphabet)**(n*m)
print(list(all_grids_of_alphabet(alphabet0, n, m))[0])
print(list(all_grids_of_alphabet(alphabet0, n, m))[-1])
[['0']] [['1']] [['0', '0'], ['0', '0']] [['1', '1'], ['1', '1']] [['0'], ['0']] [['1'], ['1']] [['0', '0']] [['1', '1']] [['0', '0', '0'], ['0', '0', '0'], ['0', '0', '0']] [['1', '1', '1'], ['1', '1', '1'], ['1', '1', '1']] [['0', '0', '0'], ['0', '0', '0']] [['1', '1', '1'], ['1', '1', '1']] [['0', '0'], ['0', '0'], ['0', '0']] [['1', '1'], ['1', '1'], ['1', '1']] [['0']] [['1']] [['0', '0'], ['0', '0']] [['1', '1'], ['1', '1']] [['0'], ['0']] [['1'], ['1']] [['0', '0']] [['1', '1']] [['0', '0', '0'], ['0', '0', '0'], ['0', '0', '0']] [['1', '1', '1'], ['1', '1', '1'], ['1', '1', '1']] [['0', '0', '0'], ['0', '0', '0']] [['1', '1', '1'], ['1', '1', '1']] [['0', '0'], ['0', '0'], ['0', '0']] [['1', '1'], ['1', '1'], ['1', '1']]
print(f"For the alphabet {alphabet0} of size = {len(alphabet0)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
%time all_these_grids = list(all_grids_of_alphabet(alphabet0, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
For the alphabet ['0', '1'] of size = 2 : CPU times: user 28 µs, sys: 6 µs, total: 34 µs Wall time: 37.9 µs For (n, m) = (1, 1) the number of grids is 2 CPU times: user 21 µs, sys: 4 µs, total: 25 µs Wall time: 29.8 µs For (n, m) = (2, 1) the number of grids is 4 CPU times: user 20 µs, sys: 4 µs, total: 24 µs Wall time: 26.5 µs For (n, m) = (1, 2) the number of grids is 4 CPU times: user 38 µs, sys: 8 µs, total: 46 µs Wall time: 48.9 µs For (n, m) = (2, 2) the number of grids is 16
How long does it take and how many grids for the easy problem?¶
print(f"For the alphabet {alphabet1} of size = {len(alphabet1)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
%time all_these_grids = list(all_grids_of_alphabet(alphabet1, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
For the alphabet {'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'} of size = 10 :
CPU times: user 73 µs, sys: 0 ns, total: 73 µs
Wall time: 80.1 µs
For (n, m) = (1, 1) the number of grids is 10
CPU times: user 303 µs, sys: 31 µs, total: 334 µs
Wall time: 341 µs
For (n, m) = (2, 1) the number of grids is 100
CPU times: user 584 µs, sys: 124 µs, total: 708 µs
Wall time: 719 µs
For (n, m) = (1, 2) the number of grids is 100
CPU times: user 27.6 ms, sys: 152 µs, total: 27.7 ms
Wall time: 27.3 ms
For (n, m) = (2, 2) the number of grids is 10000
That's still pretty small and fast!
How long does it take and how many grids for the hard problem?¶
print(f"For the alphabet {alphabet2} of size = {len(alphabet2)} :")
for (n, m) in [ (1, 1), (2, 1), (1, 2), (2, 2) ]:
%time all_these_grids = list(all_grids_of_alphabet(alphabet2, n, m))
print(f"For (n, m) = {(n, m)} the number of grids is {len(all_these_grids)}")
For the alphabet {'Z', 'E', 'I', 'V', 'R', 'A', 'F', 'D', 'Q', '3', 'Y', 'L', '4', 'W', '$', '5', 'M', 'B', 'N', '2', '8', '1', 'T', 'X', 'H', '-', 'S', '?', 'G', '9', 'U', 'P', '7', 'O', '.', 'C', 'J', 'K', '0', '6', ':'} of size = 41 :
CPU times: user 1.05 ms, sys: 224 µs, total: 1.28 ms
Wall time: 1.28 ms
For (n, m) = (1, 1) the number of grids is 41
CPU times: user 2.67 ms, sys: 0 ns, total: 2.67 ms
Wall time: 2.68 ms
For (n, m) = (2, 1) the number of grids is 1681
CPU times: user 4.54 ms, sys: 30 µs, total: 4.57 ms
Wall time: 4.58 ms
For (n, m) = (1, 2) the number of grids is 1681
CPU times: user 6.39 s, sys: 191 ms, total: 6.59 s
Wall time: 6.58 s
For (n, m) = (2, 2) the number of grids is 2825761
41**(2*3)
4750104241
Just for $(n, m) = (2, 2)$ it takes about 7 seconds... So to scale for $(n, m) = (5, 5)$ would just take... WAY TOO MUCH TIME!
n, m = 5, 5
41**(5*5)
20873554875923477449109855954682643681001
import math
math.log10(41**(5*5))
40.31959641799339
For a grid of size $(5,5)$, the number of different possible grids is about $10^{40}$, that is CRAZY large, we have no hope of solving this problem with a brute force approach.
How much time would that require, just to generate the grids?
s = 7
estimate_of_running_time = 7*s * len(alphabet1)**(5*5) / len(alphabet1)**(2*2)
estimate_of_running_time # in seconds
4.9e+22
This rough estimate gives about $5 * 10^{22}$ seconds, about $10^{15}$ years, so about a million of billion years !
math.log10( estimate_of_running_time / (60*60*24*365) )
15.191389473093146
First difficult task: for each possible grid, check if its valid¶
def naive_solve(problem, alphabet, debug=False, early=True):
n, m = dimension_problem(problem)
good_grids = []
for possible_grid in all_grids_of_alphabet(alphabet, n, m):
is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early)
if is_good_grid:
if early:
return [ possible_grid ]
good_grids.append(possible_grid)
return good_grids
Let's try it!
Solving the easy problem¶
Let's check that we can quickly find one solution:
%%time
good_grids1 = naive_solve(problem1, alphabet1, debug=False, early=True)
print(f"For problem 1\n{problem1}\nOn alphabet\n{alphabet1}\n==> We found one solution:\n{good_grids1}")
For problem 1
{'left_lines': ['HE|LL|O+', '[PLEASE]+'], 'right_lines': None, 'top_columns': ['[^SPEAK]+', 'EP|IP|EF'], 'bottom_columns': None}
On alphabet
{'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}
==> We found one solution:
[[['H', 'E'], ['L', 'P']]]
CPU times: user 111 ms, sys: 3.25 ms, total: 114 ms
Wall time: 115 ms
Then can we find more solutions?
%%time
good_grids1 = naive_solve(problem1, alphabet1, debug=False, early=False)
print(f"For problem 1\n{problem1}\nOn alphabet\n{alphabet1}\n==> We found these solutions:\n{good_grids1}")
For problem 1
{'left_lines': ['HE|LL|O+', '[PLEASE]+'], 'right_lines': None, 'top_columns': ['[^SPEAK]+', 'EP|IP|EF'], 'bottom_columns': None}
On alphabet
{'S', 'P', 'E', 'O', 'L', 'H', 'I', 'K', 'A', 'F'}
==> We found these solutions:
[[['H', 'E'], ['L', 'P']]]
CPU times: user 168 ms, sys: 441 µs, total: 169 ms
Wall time: 167 ms
No there is indeed a unique solution here for the first "easy" problem!
Solving the intermediate problem¶
%%time
good_grids3 = naive_solve(problem3, alphabet3, debug=False, early=True)
print(f"For problem 3\n{problem3}\nOn alphabet\n{alphabet3}\n==> We found one solution:\n{good_grids3}")
--------------------------------------------------------------------------- KeyboardInterrupt Traceback (most recent call last) <timed exec> in <module> <ipython-input-260-3cd60b633370> in naive_solve(problem, alphabet, debug, early) 2 n, m = dimension_problem(problem) 3 good_grids = [] ----> 4 for possible_grid in all_grids_of_alphabet(alphabet, n, m): 5 is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early) 6 if is_good_grid: <ipython-input-161-8aea88f3c7d0> in all_grids_of_alphabet(alphabet, lines, columns) 9 for line in range(lines) 10 ] ---> 11 for column in range(columns) 12 ] 13 yield tr_grid <ipython-input-161-8aea88f3c7d0> in <listcomp>(.0) 9 for line in range(lines) 10 ] ---> 11 for column in range(columns) 12 ] 13 yield tr_grid KeyboardInterrupt:
That was so long...
I could try to use Pypy3 IPython kernel, to speed things up?
Yes it's possible to use a Pypy kernel from your regular Python notebook! See https://stackoverflow.com/questions/33850577/is-it-possible-to-run-a-pypy-kernel-in-the-jupyter-notebook
Solving the hard problem¶
Most probably, it will run forever if I use the naive approach of:
- generate all grids of $m$ words of size $n$ in given alphabet $\Sigma$ ;
- for all grid:
- test it using naive algorithm
- if it's valid: adds it to the list of good grids
There are $|\Sigma|^{n \times m}$ possible grids, so this approach is doubly exponential in $n$ for square grids.
I must think of a better approach... Being just exponential in $\max(m, n)$ would imply that it's practical for the harder problem of size $(5,5)$.
%%time
good_grids2 = naive_solve(problem2, alphabet2, debug=False, early=True)
print(f"For problem 2\n{problem2}\nOn alphabet\n{alphabet2}\n==> We found one solution:\n{good_grids2}")
------------------------------------------------------------------- KeyboardInterrupt Traceback (most recent call last) <timed exec> in <module> <ipython-input-170-3cd60b633370> in naive_solve(problem, alphabet, debug, early) 2 n, m = dimension_problem(problem) 3 good_grids = [] ----> 4 for possible_grid in all_grids_of_alphabet(alphabet, n, m): 5 is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early) 6 if is_good_grid: <ipython-input-161-8aea88f3c7d0> in all_grids_of_alphabet(alphabet, lines, columns) 1 def all_grids_of_alphabet(alphabet, lines, columns): ----> 2 all_words = list(itertools.product(alphabet, repeat=columns)) 3 all_words = [ "".join(words) for words in all_words ] 4 all_grids = itertools.product(all_words, repeat=lines) 5 for pre_tr_grid in all_grids: KeyboardInterrupt:
My first idea was to try to tackle each constraint independently, and generate the set of words that satisfy this contraint. (by naively checking check(constraint, word) for each word in $\Sigma^n$ or $\Sigma^m$).
- if there are two line constraints (left/right), get the intersection of the two sets of words;
- then, for each line we have a set of possible words:
- we can build each column, and then check that the top/bottom constraint is valid or not
- if valid, continue to next column until the last
- if all columns are valid, then these lines/columns form a possible grid!
- (if we want only one solution, stop now, otherwise continue)
Second difficult task: a more efficient approach to solve any problem¶
n, m = dimension_problem(problem1)
problem1
{'left_lines': ['HE|LL|O+', '[PLEASE]+'],
'right_lines': None,
'top_columns': ['[^SPEAK]+', 'EP|IP|EF'],
'bottom_columns': None}
alphabet1
{'A', 'E', 'F', 'H', 'I', 'K', 'L', 'O', 'P', 'S'}
len(list(all_words_of_alphabet(alphabet1, n)))
100
["".join(word) for word in list(all_words_of_alphabet(alphabet1, n))][:10]
['SS', 'SP', 'SE', 'SO', 'SL', 'SH', 'SI', 'SK', 'SA', 'SF']
[
[ "".join(word)
for word in all_words_of_alphabet(alphabet1, n)
if check_line(problem1, alphabet1, "".join(word), line, debug=False, early=True)
]
for line in range(m)
]
[['OO', 'LL', 'HE'], ['SS', 'SP', 'SE', 'SL', 'SA', 'PS', 'PP', 'PE', 'PL', 'PA', 'ES', 'EP', 'EE', 'EL', 'EA', 'LS', 'LP', 'LE', 'LL', 'LA', 'AS', 'AP', 'AE', 'AL', 'AA']]
[
[ "".join(word)
for word in all_words_of_alphabet(alphabet1, m)
if check_column(problem1, alphabet1, "".join(word), column, debug=False, early=True)
]
for column in range(n)
]
[['OO', 'OL', 'OH', 'OI', 'OF', 'LO', 'LL', 'LH', 'LI', 'LF', 'HO', 'HL', 'HH', 'HI', 'HF', 'IO', 'IL', 'IH', 'II', 'IF', 'FO', 'FL', 'FH', 'FI', 'FF'], ['EP', 'EF', 'IP']]
So let's write this algorithm.
I'm using a tqdm.tqdm() wrapper on the foor loops, to keep an eye on the progress.
from tqdm.notebook import trange, tqdm
def smart_solve(problem, alphabet, debug=False, early=True):
n, m = dimension_problem(problem)
good_grids = []
possible_words_for_lines = [
[ "".join(word)
for word in all_words_of_alphabet(alphabet, n)
if check_line(problem, alphabet, "".join(word), line, debug=False, early=True)
# TODO don't compute this "".join(word) twice?
]
for line in range(m)
]
number_of_combinations = 1
for line in range(m):
number_of_combinations *= len(possible_words_for_lines[line])
print(f"- There are {len(possible_words_for_lines[line])} different words for line #{line}")
print(f"=> There are {number_of_combinations} combinations of words for lines #{0}..#{m-1}")
for possible_words in tqdm(
list(itertools.product(*possible_words_for_lines)),
desc="lines"
):
if debug: print(f" Trying possible_words from line constraints = {possible_words}")
column = 0
no_wrong_column = True
while no_wrong_column and column < n:
word_column = "".join(possible_words[line][column] for line in range(m))
if debug: print(f" For column #{column}, word = {word_column}, checking constraint...")
if not check_column(problem, alphabet, word_column, column, debug=False, early=True):
# this word is NOT valid for this column, so let's go to the next word
if debug: print(f" This word {word_column} is NOT valid for this column {column}, so let's go to the next word")
no_wrong_column = False
# break: this was failing... broke the outer for-loop and not the inner one
column += 1
if no_wrong_column:
print(f" These words seemed to satisfy the column constraints!\n{possible_words}")
# so all columns are valid! this choice of words is good!
possible_grid = [
list(word) for word in possible_words
]
print(f"Giving this grid:\n{possible_grid}")
# let's check it, just in case (this takes a short time, compared to the rest)
is_good_grid = check_grid(problem, alphabet, possible_grid, debug=debug, early=early)
if is_good_grid:
if early:
return [ possible_grid ]
good_grids.append(possible_grid)
# after the outer for loop on possible_words
return good_grids
And let's try it:
For the easy problem¶
grid1_solution
[['H', 'E'], ['L', 'P']]
%%time
good_grids1 = smart_solve(problem1, alphabet1)
good_grids1
- There are 3 different words for line #0 - There are 25 different words for line #1 => There are 75 combinations of words for lines #0..#1
lines: 0%| | 0/75 [00:00<?, ?it/s]
These words seemed to satisfy the column constraints!
('HE', 'LP')
Giving this grid:
[['H', 'E'], ['L', 'P']]
CPU times: user 37.9 ms, sys: 3.77 ms, total: 41.6 ms
Wall time: 90.5 ms
[[['H', 'E'], ['L', 'P']]]
So it worked!
🚀 It was also BLAZING fast compared to the naive approach: 160ms against about 900µs, almost a 160x speed-up factor!
🤔 I don't understand why it's so slow now I did get a time of 900 µs at first try, now it's about 90 ms... just a 2x spee-up factor.
Let's try for the harder problem!
For the intermediate problem¶
%%time
#assert False # uncomment when ready
good_grids3 = smart_solve(problem3, alphabet3)
good_grids3
- There are 27 different words for line #0 - There are 24 different words for line #1 - There are 7 different words for line #2 => There are 4536 combinations of words for lines #0..#2
lines: 0%| | 0/4536 [00:00<?, ?it/s]
These words seemed to satisfy the column constraints!
('NOS', 'FER', 'ATU')
Giving this grid:
[['N', 'O', 'S'], ['F', 'E', 'R'], ['A', 'T', 'U']]
CPU times: user 92 ms, sys: 0 ns, total: 92 ms
Wall time: 90 ms
[[['N', 'O', 'S'], ['F', 'E', 'R'], ['A', 'T', 'U']]]
🚀 It was also BLAZING fast compared to the naive approach: 90ms, when the naive approach was just too long that I killed it...
For the harder problem¶
%%time
#assert False # uncomment when ready
good_grids2 = smart_solve(problem2, alphabet2)
good_grids2
For the first time seeing this regexp '[1LOVE2?4]+.', compiling it and storing in memory_of_compiled_regexps, now of size 21. For the first time seeing this regexp '(\\d+)[LA\\s$?]+', compiling it and storing in memory_of_compiled_regexps, now of size 22. For the first time seeing this regexp '(A|D)M[5-8$L]+', compiling it and storing in memory_of_compiled_regexps, now of size 23. For the first time seeing this regexp '(\\-P|5\\$|AM|Z|L)+', compiling it and storing in memory_of_compiled_regexps, now of size 24. For the first time seeing this regexp '[^\\s0ILAD]+', compiling it and storing in memory_of_compiled_regexps, now of size 25. For the first time seeing this regexp '(\\-D|\\-WE)+[^L4-9N$?]+', compiling it and storing in memory_of_compiled_regexps, now of size 26. For the first time seeing this regexp '[B-E]+(.)\\1.', compiling it and storing in memory_of_compiled_regexps, now of size 27. For the first time seeing this regexp '[FED$?]+', compiling it and storing in memory_of_compiled_regexps, now of size 28.
It made my kernel restart...
Improve the solution - TODO¶
If you're extra curious about this puzzle problem, and my experiments, you can continue from here and finish these ideas:
It could be great if it were be possible to give a partially filled grid, and start from there.
It could also be great to just be able to fill one cell in the grid, in case you're blocked and want some hint.
My feeling about these problems and my solutions¶
I could have tried to be more efficient, but I didn't have much time to spend on this.
Conclusion¶
That was nice! Writing this notebook took about 4.5 hours entirely, from first idea to final edit, on Sunday 28th of February, 2021. (note that I was also cooking my pancakes during the first half, so I wasn't intensely coding)
Have a look at my other notebooks.
