Spin frustration¶
In [1]:
from sympy.interactive import printing
printing.init_printing(use_latex = True)
import numpy as np
import sympy as sp
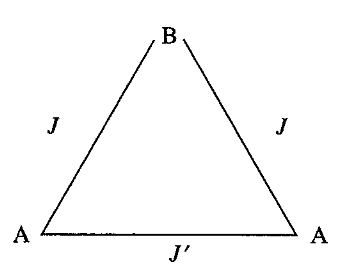
Two equal A-B interactions and one A-A interaction. The local spins are $S_{a1}$, $S_{a2}$ ($S_{a1}$ = $S_{a2}$ = $S_{a}$) and $S_{b}$. Interactions parameters are $J$ and $J'$.
The spin Hamiltonian in zero field is:
$$H = -J(S_{a1} \dot S_{b} + S_{a2} \dot S_{b}) - J'(S_{a1} \dot S_{a2})$$Negrecting anisotropic interactions:
$$H = -J(S_{a1} \dot S_{b} + S_{a2} \dot S_{b} + S_{a1} \dot S_{a2}) - (J'-J)(S_{a1} \dot S_{a2})$$Or:
$$H = -\frac{J}{2}(S^{2} - S_{a1}^{2} - S_{a2}^{2} - S_{b}^{2}) - \frac{J'-J}{2}(S'^{2} - S_{a1}^{2} - S_{a2}^{2})$$In [2]:
# Assignment of all symbolic variables
Sa = sp.Symbol("Sa")
Sa1 = sp.Symbol("Sa1")
Sa2 = sp.Symbol("Sa2")
Sb = sp.Symbol("Sb")
J = sp.Symbol("J")
J_prime = sp.Symbol("J\'")
S_prime = Sa1 + Sa2
S = S_prime + Sb
In [3]:
# Phythonic version of the Hamiltonian (Here it's showed expanded)
H = (-J/2)*(S**2 - Sa1**2 - Sa2**2 - Sb**2) - ((J_prime - J)/2)*(S_prime**2 - Sa1**2 - Sa2**2)
display(H)
$$- \frac{J}{2} \left(- Sa_{1}^{2} - Sa_{2}^{2} - Sb^{2} + \left(Sa_{1} + Sa_{2} + Sb\right)^{2}\right) - \left(- \frac{J}{2} + \frac{J'}{2}\right) \left(- Sa_{1}^{2} - Sa_{2}^{2} + \left(Sa_{1} + Sa_{2}\right)^{2}\right)$$
Relative energies in Zero Field: $$E(S,S')=-\frac{J}{2}S(S+1) - \frac{J'-J}{2}S'(S'+1)$$ With:
$$S' = S_{a1} + S_{a2}$$$$S = S' + S_{b}$$In [4]:
# Pythonic version of the energy equation
E = (-J/2)*(S*(S + 1)) - ((J_prime -J)/2)*(S_prime*(S_prime + 1))
display(E)
$$- \frac{J}{2} \left(Sa_{1} + Sa_{2} + Sb\right) \left(Sa_{1} + Sa_{2} + Sb + 1\right) - \left(- \frac{J}{2} + \frac{J'}{2}\right) \left(Sa_{1} + Sa_{2}\right) \left(Sa_{1} + Sa_{2} + 1\right)$$
In [5]:
# And the expanded version of the equation:
display(sp.expand(E))
$$- J Sa_{1} Sb - J Sa_{2} Sb - \frac{J Sb^{2}}{2} - \frac{J Sb}{2} - \frac{J' Sa_{1}^{2}}{2} - J' Sa_{1} Sa_{2} - \frac{J' Sa_{1}}{2} - \frac{J' Sa_{2}^{2}}{2} - \frac{J' Sa_{2}}{2}$$
S' varies by an integer from 0 to $2S_{a}$ and for every S' value S varies by an integer from $|S'-S_{b}|$ to $S'+S_{b}$
In [6]:
# Entre valores numéricos para os spins
Sa = 1/2
Sb = 1/2
Sa1 = Sa
Sa2 = Sa
S_prime = np.arange(0, 2*Sa + 1, 1)
Sba = np.amin(np.absolute(S_prime - Sb))
Sbb = np.amax(S_prime + Sb)
S = np.arange(np.amin(np.absolute(S_prime - Sb)), np.amax(S_prime + Sb + 1), 1)
print("S = {} e S' = {}".format(S, S_prime))
S = [0.5 1.5] e S' = [0. 1.]
In [7]:
# Iterativamente encontrando valores para as energias
for i in S_prime:
S = np.arange(np.amin(np.absolute(i - Sb)), np.amax(i + Sb + 1), 1)
for j in S:
print("E({},{})".format(j, i))
E = -(J/2)*(j*(j + 1)) - ((J_prime -J)/2)*(i*(i + 1))
display(E)
E(0.5,0.0)
$$- 0.375 J$$
E(0.5,1.0)
$$0.625 J - 1.0 J'$$
E(1.5,1.0)
$$- 0.875 J - 1.0 J'$$
In [ ]:
In [ ]: