Center of Mass and Moment of Inertia¶
Renato Naville Watanabe, Marcos Duarte
Laboratory of Biomechanics and Motor Control
Federal University of ABC, Brazil
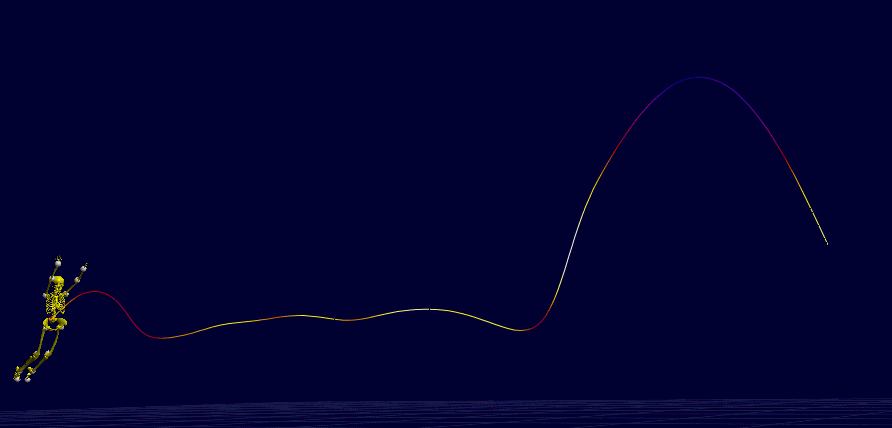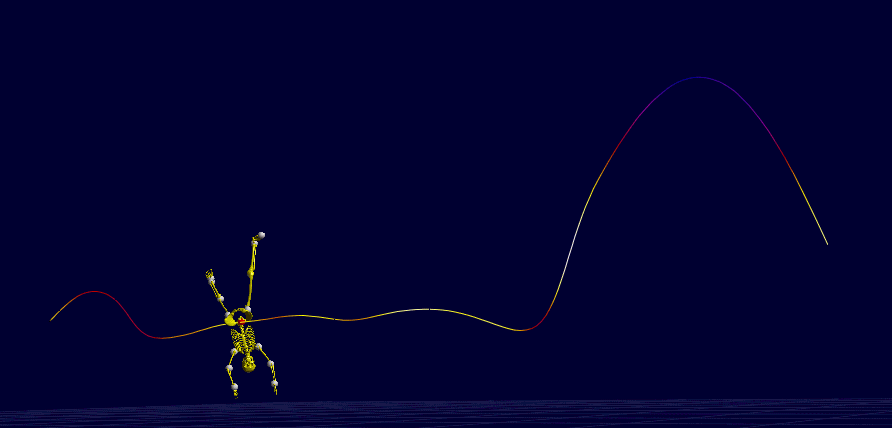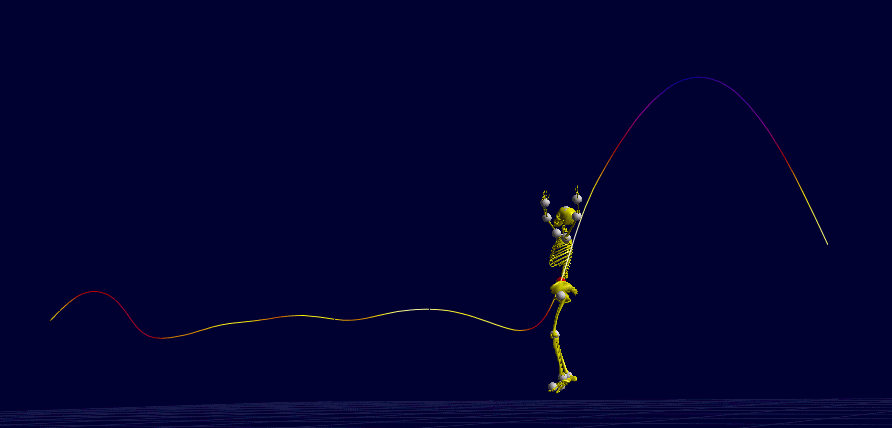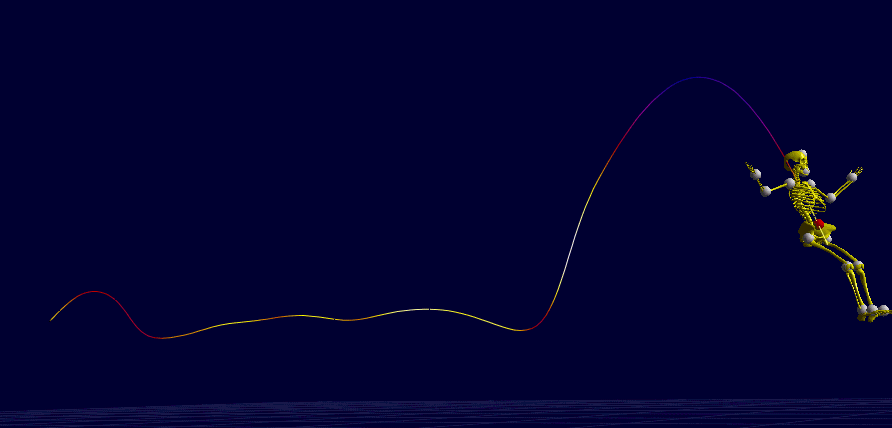
I: While her body translates and rotates in varied ways, the trajectory of the body center of mass is always a parabola during the aerial phases (minus some experimental error).
II: To execute the double front flip at the last jump, she increases the body angular speed by flexing the hips (piked position), which decreases the body moment of inertia — she knows the law of conservation of angular momentum.
Note the view is not from a right angle to the sagittal plane (Image from BMClab).
Contents
- 1 Python setup
- 2 Center of mass
- 3 Center of gravity
- 4 Geometric center
- 5 Moment of rotational inertia
- 6 Further reading
- 7 Video lectures on the internet
- 8 Problems
- 9 References
Python setup¶
# import the necessary libraries
import numpy as np
import sympy as sym
from IPython.display import display, Math
from sympy.vector import CoordSys3D
Code for using LaTeX commands, see https://github.com/jupyterlab/jupyterlab/pull/5997 and https://texfaq.org/FAQ-patch.
$\require{begingroup}\require{renewcommand}$ $\gdef\hat#1{\widehat{\mathbf{#1}}}$
$\require{begingroup}\require{newcommand}$ $\gdef\vecb#1{\vec{\bf{#1}}}$
\vskip-\parskip \vskip-\baselineskip
Execute this cell to format a versor with a hat and bold font or edit it to add custom commands.
Center of mass¶
Set of particles¶
The center of mass of a set of particles is defined as the point (position) where the sum of the vectors linking this point to each particle, weighted by its mass, is zero. By mass we mean the inertial mass, a quantitative measure of an object's resistance to linear acceleration.
Consider the set of particles shown below.
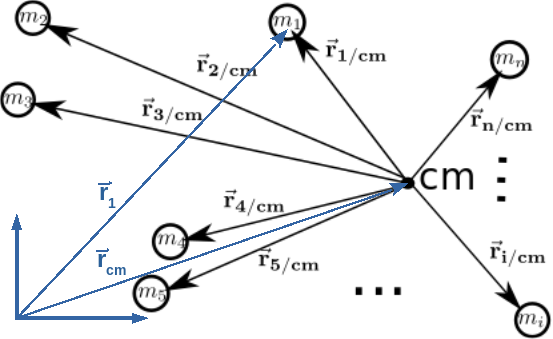
The sum of the vectors linking the center of mass to each particle is:
\begin{equation} \begin{array}{l} \sum\limits_{i=1}^nm_i{\vec{r}_{i/cm}} &= \sum\limits_{i=1}^nm_i\left({\vec{r}_i} - {\vec{r}_{cm}}\right) \\ &= \sum\limits_{i=1}^nm_i{\vec{r}_i} - \sum\limits_{i=1}^nm_i{\vec{r}_{cm}} \\ &= \sum\limits_{i=1}^nm_i{\vec{r}_i} - {\vec{r}_{cm}}\sum\limits_{i=1}^nm_i \label{} \end{array} \end{equation}where $n$ is the number of particles.
Now, we equal this sum to zero and isolate ${\vec{r}_{cm}}$:
\begin{equation} \begin{array}{l} \sum\limits_{i=1}^nm_i{\vec{r}_i} - {\vec{r}_{cm}}\sum\limits_{i=1}^nm_i = 0 \quad \longrightarrow \\ \begin{aligned} \vec{r}_{cm} &= \dfrac{\sum\limits_{i=1}^nm_i{\vec{r}_i}}{\sum\limits_{i=1}^nm_i} &\phantom{=} \\ &= \dfrac{\sum\limits_{i=1}^nm_i{\vec{r}_i}}{m_T} \end{aligned} \label{} \end{array} \end{equation}where $m_T$ is the total mass of the particles.
Example: Two particles¶
Consider two particles with masses $m_1$ and $m_2$, the center of mass of the system is:
\begin{equation} \begin{array}{l} \vec{r}_{cm} &= \dfrac{m_1\vec{r}_1 + m_2\vec{r}_2}{m_1+m_2} \\ &= \dfrac{m_1\vec{r}_1 + m_2\vec{r}_1 - m_2\vec{r}_1 + m_2\vec{r}_2}{m_1+m_2} \\ &= \dfrac{(m_1+m_2)\vec{r}_1}{m_1+m_2} + \dfrac{m_2(\vec{r}_2 - \vec{r}_1)}{m_1+m_2} \\ \vec{r}_{cm} &= \vec{r}_1 + \dfrac{m_2}{m_1+m_2}(\vec{r}_2 - \vec{r}_1) \label{} \end{array} \end{equation}Can you guess what is the expression above if we rewrite it in relation to vector $\vec{r}_{2}$, i.e., $\vec{r}_{cm} = \vec{r}_{2} + \ldots$ ?
Rigid body¶
For a rigid body, the center of mass is defined as the point where the integral of the vectors linking this point to each differential part of mass, weighted by this differential mass, is zero.
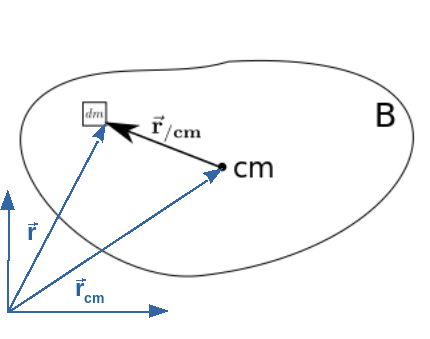
This integral is:
\begin{equation} \begin{array}{l} \int\limits_{B} {\vec{r}_{/cm}} \mathrm d m &= \int\limits_{B}(\vec{r}-\vec{r}_{cm}) \mathrm d m \\ &= \int\limits_{B} {\vec{r}}\,\mathrm d m - \int\limits_{B}{\vec{r}_{cm}} \mathrm d m \\ &= \int\limits_{B} {\vec{r}}\,\mathrm d m - {\vec{r}_{cm}}\int\limits_{B}\, \mathrm d m \label{} \end{array} \end{equation}Now we equal this integral to zero and isolate $\vec{r}_{cm}$:
\begin{equation} \begin{array}{l} \int\limits_{B} \vec{r}\,\mathrm d m - \vec{r}_{cm}\int\limits_{B}\, \mathrm d m = 0 \longrightarrow \\ \vec{r}_{cm} = \dfrac{\int\limits_{B}{\vec{r}}\,\mathrm d m}{\int\limits_{B}\, \mathrm d m} = \dfrac{ \int\limits_{B} \vec{r}\,\mathrm d m}{m_B} \label{eq:cm} \end{array} \end{equation}where $m_B$ is the mass of the body.
Example: Bar¶
Let's calculate the center of mass of a homogeneous (with equal density) bar shown below.
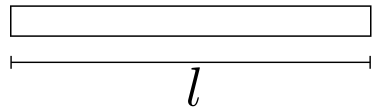
The mass of the bar is:
\begin{equation} m = \rho l \end{equation}The integral can be computed as:
\begin{equation} \int \vec{r}\,\mathrm d m = \rho\int\limits_0^l x\,\mathrm d x =\rho\frac{l^2}{2} \end{equation}So, the center of mass of the bar is:
\begin{equation} \vec{r}_{cm} = \dfrac{\rho\dfrac{l^2}{2}}{\rho l} = \dfrac{l}{2} \end{equation}The center of mass of a homogeneous bar is in the middle of the bar.
A key aspect in the calculation of the integral above is to transform the differential of the variable mass $\mathrm d m$ into the differential of the variable displacement $\mathrm d x$ (or area or volume for a surface or a solid) because the body's density is known.
Let's use Sympy, a symbolic library in Python, to solve this integral.
A definite integral of integrand f with respect to variable x over interval [a,b] can be calculated with the function integrate:
sym.integrate(f, (x, a, b))
# Helping function
def print2(lhs, rhs):
"""Rich display of Sympy expression as lhs = rhs."""
display(Math(r'{} = '.format(lhs) + sym.latex(sym.simplify(rhs, ratio=1.7))))
# define variables
x = sym.symbols('x')
rho, ell = sym.symbols('rho ell', positive=True)
m = rho*ell
# solve the integral
rcm = rho * sym.integrate(x, (x, 0, ell))/m
print2('\\vec{r}_{cm}', rcm)
Example: Triangle¶
Let's compute the center of mass of the triangle shown below.
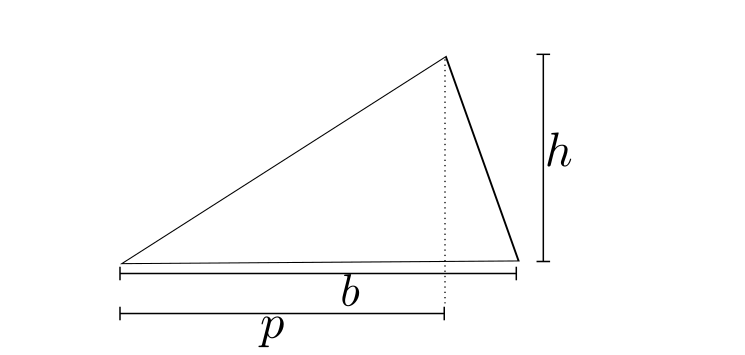
The center of mass is given by Eq.(\ref{eq:cm}):
\begin{equation} \vec{r}_{cm} = \frac{\int \vec{r}\,\mathrm d m}{m} \label{eq:int_area} \end{equation}The mass of the triangle w.r.t. its density and dimensions is equal to:
\begin{equation} m = \rho A = \frac{\rho bh}{2} \end{equation}In Eq.(\ref{eq:int_area}), the differential of the variable mass $\mathrm d m$ will be transformed into the differential of the variable area $\mathrm d A$, which in turn is calculated as $\mathrm d x \mathrm d y$, resulting in a double integral:
\begin{equation} \int \vec{r}\,\mathrm d m = \rho\int \vec{r}\,\mathrm d A = \rho \int\limits_x \int\limits_y (x\hat{i} + y\hat{j})\,\mathrm d y \mathrm d x \label{} \end{equation}The integral can be computed by separating it into two parts: one part we integrate in the $x$ direction from $0$ to $p$, and the other part from $p$ to $b$. The integration in the $y$ direction will be from $0$ to $\frac{xh}{p}$ in the first part and from $0$ to $\frac{(b-x)h}{b-p}$ in the second part:
\begin{equation} \int \vec{r}\,\mathrm d m = \rho\left[\int\limits_0^p\int\limits_0^\frac{xh}{p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x + \int\limits_p^b\int\limits_0^\frac{(b-x)h}{b-p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x\right] \label{} \end{equation}So, the center of mass of the triangle will be:
\begin{equation} \begin{array}{l} \vec{r}_{cm} &= \dfrac{\rho\left[\int\limits_0^p\int\limits_0^\frac{xh}{p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x + \int\limits_p^b\int\limits_0^\frac{(b-x)h}{b-p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x\right]}{\dfrac{\rho bh}{2}} \\ &= \dfrac{2\left[\int\limits_0^p\int\limits_0^\frac{xh}{p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x + \int\limits_p^b\int\limits_0^\frac{(b-x)h}{b-p} (x\hat{i} + y\hat{j}) \,\mathrm d y\mathrm d x\right]}{bh} \label{} \end{array} \end{equation}The integral above will be solved using the Symbolic library of the Python.
# define variables
G = CoordSys3D('')
x, y = sym.symbols('x, y')
rho, h, p, b = sym.symbols('rho, h, p, b', positive=True)
# solve the integral
# for x
xcm = 2*(sym.integrate(sym.integrate(x, (y, 0, x*h/p)), (x, 0, p)) +
sym.integrate(sym.integrate(x, (y, 0, (b-x)*h/(b-p))), (x, p, b)))/(b*h)
# for y
ycm = 2*(sym.integrate(sym.integrate(y, (y, 0, x*h/p)), (x, 0, p)) +
sym.integrate(sym.integrate(y, (y, 0, (b-x)*h/(b-p))), (x, p, b)))/(b*h)
print2('x_{cm}', xcm)
print2('y_{cm}', ycm)
Finally, the center of mass of the triangle is:
print2('\\vec{r}_{cm}', xcm*G.i + ycm*G.j)
Center of mass of a complex system¶
Now, we will consider a set of $n$ bodies. The center of mass of this set of bodies can be computed by integrating the Eq.(\ref{eq:cm}) over all bodies:
\begin{equation} \begin{array}{l} \vec{r}_{cm} &= \dfrac{ \int\limits_{B1,B2,\ldots,Bn}\vec{r}\,\mathrm d m}{m_{B1}+m_{B2}+ \ldots + m_{Bn}} \\ &= \dfrac{\int\limits_{B1}\vec{r}\,\mathrm d m+\int\limits_{B2}\vec{r}\,dm+\ldots+\int\limits_{Bn}\vec{r}\,\mathrm d m}{m_{B1}+m_{B2}+\ldots+ m_{Bn}} \\ &= \dfrac{\dfrac{\int\limits_{B1}\vec{r}\,\mathrm d m}{m_{B1}}m_{B1} + \dfrac{\int\limits_{B2}\vec{r}\,\mathrm d m}{m_{B2}}m_{B2} +\ldots+ \dfrac{\int\limits_{Bn}\vec{r}\,\mathrm d m}{m_{Bn}}m_{Bn}}{m_{B1}+m_{B2}+\ldots+ m_{Bn}} \\ &= \dfrac{\vec{r}_{cm_1} m_{B1} + \vec{r}_{cm_2}m_{B2} +\ldots+ \vec{r}_{cm_n}m_{Bn}}{m_{B1}+m_{B2}+\ldots+ m_{Bn}} \\ \vec{r}_{cm} &= \dfrac{\vec{r}_{cm_1} m_{B1} + \vec{r}_{cm_2}m_{B2} +\ldots+ \vec{r}_{cm_n}m_{Bn}}{m_T} \label{} \end{array} \end{equation}where $\vec{r}_{cm_i}$ is the center of mass of the body $i$, $m_{Bi}$ is the mass of the body $i$ and $m_T$ is the total mass of all bodies.
The expression above shows that we can interpret each body as a particle with its mass and position.
Example: Three bars¶
Let's compute the center of mass of the system shown below.

The system can be seen as a set of three bars; we can compute the center of mass by considering each bar as a particle located at its respective center of mass.
We have previously computed the center of mass of a homogeneous bar as being at its center. So, the center of mass of each bar of the system is:
\begin{equation} \begin{array}{l} \vec{r}_{cm_1} &= -\frac{l_1}{2}\hat{j} \\ \vec{r}_{cm_2} &= \frac{l_2}{2}\sin(\theta_1)\hat{i}-\frac{l_2}{2}\cos(\theta_1)\hat{j} \\ \vec{r}_{cm_3} &= l_2\sin(\theta_1)\hat{i}-l_2\cos(\theta_1)\hat{j}+\frac{l_3}{2}\sin(\theta_2)\hat{i}-\frac{l_3}{2}\cos(\theta_2)\hat{j} \\ &= \left(l_2\sin(\theta_1)+\frac{l_3}{2}\sin(\theta_2) \right)\hat{i} + \left(l_2\cos(\theta_1)-\frac{l_3}{2}\cos(\theta_2) \right)\hat{j} \label{} \end{array} \end{equation}So, the center of mass of the system is:
\begin{equation} \begin{array}{l} \vec{r}_{cm} &= \dfrac{m_1 \vec{r}_{cm_1}+m_2 \vec{r}_{cm_2}+m_3 \vec{r}_{cm_3}}{m_1+m_2+m_3} \\ &= \dfrac{-m_1\frac{l_1}{2}\hat{j} + m_2(\frac{l_2}{2}\sin(\theta_1)\hat{i}-\frac{l_2}{2}\cos(\theta_1)\hat{j})+m_3 \left[\left(l_2\sin(\theta_1)+\frac{l_3}{2}\sin(\theta_2) \right)\hat{i} + \left(l_2\cos(\theta_1)-\frac{l_3}{2}\cos(\theta_2) \right)\hat{j} \right]}{m_1+m_2+m_3} \\ &= \dfrac{m_2\frac{l_2}{2}\sin(\theta_1)\hat{i}+m_3 \left(l_2\sin(\theta_1)+\frac{l_3}{2}\sin(\theta_2) \right)\hat{i}}{m_1+m_2+m_3}+\dfrac{-m_1\frac{l_1}{2}\hat{j} - m_2\frac{l_2}{2}\cos(\theta_1)\hat{j}+m_3 \left(l_2\cos(\theta_1)-\frac{l_3}{2}\cos(\theta_2) \right)\hat{j}}{m_1+m_2+m_3} \\ \vec{r}_{cm} &= \dfrac{m_2\frac{l_2}{2}\sin(\theta_1)+m_3 \left(l_2\sin(\theta_1)+\frac{l_3}{2}\sin(\theta_2)\right)}{m_1+m_2+m_3}\hat{i}+\dfrac{-m_1\frac{l_1}{2} - m_2\frac{l_2}{2}\cos(\theta_1)+m_3 \left(l_2\cos(\theta_1)-\frac{l_3}{2}\cos(\theta_2) \right)}{m_1+m_2+m_3}\hat{j} \label{} \end{array} \end{equation}Center of gravity¶
Center of gravity of a body is the point where the moment of force caused by the gravitational force in the whole body relative to this point is zero.
For the body $B$, this the moment of force is:
If the acceleration of gravity being applied to the whole body is the same (for all practical purposes, in Biomechanics we can consider it the same in the whole body), the gravity vector can go out of the integral:
\begin{equation} \begin{array}{l} \vec{M}_0 &= \int\limits_{B}\vec{r}_B \, \mathrm d m\, \times\, \vec{g} \\ &= \int\limits_{B}(\vec{r} - \vec{r}_{cm})\,\mathrm d m\, \times\, \vec{g} \\ &= \left(\int\limits_{B}\vec{r} \, \mathrm d m -\int\limits_{B}\vec{r}_{G} \, \mathrm d m \, \right) \times \, \vec{g} \label{} \end{array} \end{equation}Now, we equal this moment to zero and isolate $\vec{r}_G$:
\begin{equation} \begin{array}{l} \left(\int\limits_{B}\vec{r}\,\mathrm d m -\int\limits_{B}\vec{r}_G\,\mathrm d m\right) \times\,\vec{g} = 0 \longrightarrow \\ \int\limits_{B}\vec{r}\,\mathrm d m -\int\limits_{B}\vec{r}_G\,\mathrm d m = 0 \longrightarrow \\ \int\limits_{B}\vec{r}\,\mathrm d m -\vec{r}_G\int\limits_{B}\,\mathrm d m = 0\,\,\,\,\,\, \longrightarrow \\ \vec{r}_G = \dfrac{ \int\limits_{B}\vec{r}\,\mathrm d m}{\int\limits_{B}\,\mathrm d m} = \dfrac{ \int\limits_{B}\vec{r}\,\mathrm d m}{m_B} \label{} \end{array} \end{equation}where $m_B$ is the mass of the body.
Note that in this case, when the gravitational acceleration is constant, the center of gravity $\vec{r}_G$ is equal to the center of mass $\vec{r}_{cm}$.
Geometric center¶
For a rigid body, the geometric center is defined as the point where the integral of the vectors linking this point to each differential part of volume is zero.
This integral for a body $B$ is:
\begin{equation} \begin{array}{l} \int\limits_{B} \vec{r}_{/gc} \mathrm d V &= \int\limits_{B} (\vec{r} - \vec{r}_{gc}) \mathrm d V \\ &= \int\limits_{B} \vec{r}\, \mathrm d V - \int\limits_{B}\vec{r}_{gc}\, \mathrm d V \\ &= \int\limits_{B} \vec{r}\, \mathrm d V - \vec{r}_{gc}\int\limits_{B}\, \mathrm d V \label{} \end{array} \end{equation}Now we equal this integral to zero and isolate $\vec{r}_{gc}$:
\begin{equation} \begin{array}{l} \int\limits_{B} {\vec{r}}\,\mathrm d V - {\vec{r}_{gc}}\int\limits_{B}\, \mathrm d V = 0 \longrightarrow \\ \vec{r}_{gc} = \dfrac{ \int\limits_{B} \vec{r}\,\mathrm d V}{\int\limits_{B}\, \mathrm d V} = \dfrac{ \int\limits_{B} \vec{r}\,\mathrm d V}{V} \label{eq:gc} \end{array} \end{equation}where $V$ is the volume of the body.
Note that when the body has a constant density $\rho$, the center of mass is equal to the geometric center:
Moment of rotational inertia¶
The moment of rotational inertia (or moment of inertia or rotational inertia), equivalent to mass for linear motion, is a quantitative measure of the resistance to rotational acceleration around an axis of a distribution of mass in space.
Consider the linear momentum of a particle in motion, by definition:
\begin{equation} \vec{p} = m\vec{v} \label{} \end{equation}The angular momentum of a particle in rotational motion, by definition is:
\begin{equation} \vec{H}_{/O} = \vec{r} \times \vec{p} \label{} \end{equation}where $\vec{r}$ is the position of the particle relative to the chosen origin $O$.
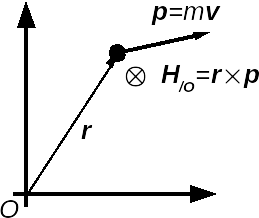
For simplicity (later we will generalize this problem), let's consider that the particle rotates at a fixed plane and at a fixed distance, $r$, to point $O$ (i.e., circular motion). In this case, the magnitude of the angular momentum is:
\begin{equation} \begin{array}{l} H_{/O} &= r \, p \\ &= r \, m \, v \\ &= r \, m \, \omega \, r \\ H_{/O} &= m \, r^2 \, \omega \end{array} \label{} \end{equation}where $\omega$ is the angular speed of rotation.
Equivalent to the linear momentum, defined as mass (inertia) times velocity, in the equation above, the term in the right-hand side that multiplies the angular velocity is defined as the rotational inertia or moment of inertia of the particle around axis passing through point $O$:
\begin{equation} I_O = m r^2 \label{} \end{equation}The value of the moment of inertia is a single positive scalar for a planar rotation or a tensor (a 3×3 inertia matrix) for a three-dimensional rotation (we will see that later). Its dimension is $[M][L]^2$ and its SI unit is $kgm^2$.
Set of particles¶
For a system of $n$ particles, the moment of inertia around a fixed axis passing by point $O$ for the case of planar rotation will be simply the sum of the moment of inertia of each particle:
\begin{equation} I_O = \sum_{i=1}^n m_{i}r_{i/O}^2 \label{eg:I} \end{equation}Example: System with two particles¶
Calculate the moment of inertia of a system composed of two particles, each with 2-kg mass and spaced by 1 m, rotating around an axis perpendicular to the line that joins the two particles and passing through: a) center of mass of the system and b) one of the masses.
The center of mass of the system is at the center (centroid) of the system. Using this position as the origin of the system, the moment of inertia of the system around its center of mass is:
$$ I_{cm} = 2 \times (0.5)^2 + 2 \times (0.5)^2 = 1 \, kgm^2 $$And around one of the masses:
$$ I_{m_1} = 2 \times (0)^2 + 2 \times (1)^2 = 2 \, kgm^2 $$Rigid body¶
In analogy to the determination of the center of mass, the moment of inertia of a rigid body around an axis passing through a point $O$ in the case of a planar rotation is given by the integral of the squared distance over the distribution of mass of the body:
\begin{equation} \begin{array}{l} I_O = \int\limits r^2_{/O} \,\mathrm d m \\ I_O = \int\limits (x^2_{/O}+y^2_{/O})\,\mathrm d m \label{} \end{array} \end{equation}For planar movements, we usually compute the moment of inertia relative to the $z$ axis (the axis perpendicular to the plane) and the point to compute the moment of inertia is the body center of mass (later we will see a simple form to calculate the moment of inertia around any axis parallel to the axis passing through the body center of mass). So, a common notation is:
\begin{equation} \begin{array}{l} I^{cm}_{zz} = \int\limits (x^2_{/cm}+y^2_{/cm})\,\mathrm d m \label{eq:inmomzzo} \end{array} \end{equation}The double $z$ in fact has a special meaning that will be clear when we consider possible rotations in three-dimensions.
Example: Bar¶
Let's compute the moment of inertia relative to the center of mass for the same bar we computed its center of mass.
The moment of inertia relative to the center of mass is:
\begin{equation} \begin{array}{l} I_{zz}^{cm} &= \int\limits x_{/cm}^2\,\mathrm d m \\ &= \int\limits_{-l/2}^{l/2} x^2\rho\,\mathrm d x \\ &= \rho\left.\left(\dfrac{x^3}{3}\right)\right|_{-l/2}^{l/2} \\ &= \rho\left(\dfrac{l^3}{24}+\dfrac{l^3}{24}\right) \\ &= \rho\dfrac{l^3}{12} \\ I_{zz}^{cm} &= \dfrac{ml^2}{12} \label{} \end{array} \end{equation}Or using the Sympy library:
# define variables
x = sym.symbols('x')
m1, rho, ell = sym.symbols('m, rho, ell', positive=True)
m = rho*ell
# solve the integral
Icm = rho * sym.integrate(x**2, (x, -ell/2, ell/2))/m
print2('I_{zz}^{cm}', Icm*m1)
Radius of gyration¶
Radius of gyration is defined as the distance that a particle would be from the a point $O$ to have the same moment of inertia that the body has. So, the radius of gyration is defined as:
\begin{equation} \begin{array}{l} r_{gyr} = \sqrt{\dfrac{I_{zz}^{cm}}{m}} \label{} \end{array} \end{equation}Example: Bar¶
For a homogeneous bar with length $l$, the radius of gyration is:
\begin{equation} \begin{array}{l} r_{gyr} = \sqrt{\dfrac{\dfrac{ml^2}{12}}{m}}=\sqrt{\dfrac{l^2}{12}} = \dfrac{l\sqrt{3}}{6} \label{} \end{array} \end{equation}This means that for the bar, the moment of inertia around an axis passing by its center of mass is the same as of a particle with equal mass but located at $r_{gyr}$ from this axis.
Parallel axis theorem¶
If we have computed the moment of inertia relative to the center of mass for an axis, for example the $z$ axis, and now want to compute the moment of inertia relative to another point $O$ for an axis parallel to the first, there is an expression to aid the computation of this moment of inertia.
In the figure below, the axis is perpendicular to the plane.
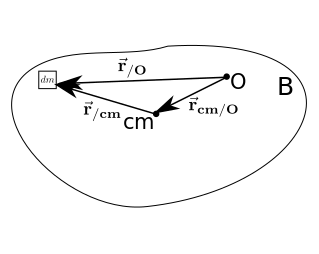
The moment of inertia relative to the axis passing through the point O is given by:
\begin{equation} \begin{array}{l} I_{zz}^O &= \int\limits_B x_{/O}^2+y_{/O}^2\,\mathrm d m \\ &= \int\limits_B (x_{/cm}+x_{cm/O})^2+(y_{/cm}+y_{cm/O})^2\,\mathrm d m \\ &= \int\limits_B x_{/cm}^2+2x_{/cm}x_{cm/O}+x_{cm/O}^2+y_{/cm}^2+2y_{/cm}y_{cm/O}+y_{cm/O}^2\,\mathrm d m \\ &=\underbrace{\int\limits_B x_{/cm}^2+y_{/cm}^2\,\mathrm d m}_{I_{zz}^{cm}} +\int\limits_B 2x_{/cm}x_{cm/O}\,\mathrm d m+\int\limits_B x_{cm/O}^2+y_{cm/O}^2\,\mathrm d m + \int\limits_B 2y_{/cm}y_{cm/O}\,\mathrm d m \\ &= I_{zz}^{cm} +2x_{cm/O}\underbrace{\int\limits_B x_{/cm}\,\mathrm d m}_{0}+\underbrace{\vphantom{\int\limits_B}(x_{cm/O}^2+y_{cm/O}^2)}_{d^2}\underbrace{\int\limits_B \,\mathrm d m \vphantom{\Bigg)}}_{m_B} + 2y_{cm/O} \underbrace{\int\limits_B y_{/cm}\,\mathrm d m}_{0} \\ I_{zz}^{O} &= I_{zz}^{cm} + m_B\,d^2 \label{} \end{array} \end{equation}The terms $\int\limits_B x_{/cm}\,\mathrm d m$ and $\int\limits_B y_{/cm}\,\mathrm d m$ are equal to zero because of the definition of center of mass. The term $d$ is the distance between the two axes.
Note that this theorem is valid only for parallel axes and the original axis passes through the center of mass.
Example: Bar¶
Let's compute the moment of inertia of a bar relative to one of its extremities, by using the parallel axis theorem.
\begin{equation} \begin{array}{l} I_{zz}^O &= I_{zz}^{cm} + m\left(\dfrac{l}{2}\right)^2 \\ &= \dfrac{ml^2}{12} + \dfrac{ml^2}{4} = \dfrac{ml^2}{3} \label{} \end{array} \end{equation}Verify that for the example where we calculated the moment of inertia of a system with two particles in relation to axes passing by different points, we could have used the parallel axis theorem.
Moment of inertia of a complex system¶
To compute the moment of inertia of a set o $n$ bodies relative to a point $O$ for a given axis (for example, the $z$ axis), we must apply the Eq.(\ref{eq:inmomzzo}) for all bodies:
\begin{equation} \begin{array}{l} I_{zz}^{O} &= \int\limits_{B1,B2,\ldots,Bn} x_{/O}^2+y_{/O}^2\,\mathrm d m \\ &= \int\limits_{B1} x_{/O}^2+y_{/O}^2\,\mathrm d m +\int\limits_{B2} x_{/O}^2+y_{/O}^2\,\mathrm d m +\ldots+\int\limits_{Bn} x_{/O}^2+y_{/O}^2\,\mathrm d m \label{} \end{array} \end{equation}Now, using the parallel axis theorem, we can write the equation above in terms of the moment of inertia relative to the center of mass of each body:
\begin{equation} \begin{array}{l} I_{zz}^{O} &= I_{zz_{B1}}^{cm_1} + m_{B1}.||\vec{r}_{cm_1/O}||^2 +I_{zz_{B2}}^{cm_2} + m_{B2}.||\vec{r}_{cm_2/O}||^2 +\ldots + I_{zz_{Bn}}^{cm_n} + m_{Bn}.||\vec{r}_{cm_n/O}||^2 \label{eq:paral} \end{array} \end{equation}where $I_{zz_{Bi}}^{cm_i}$ is the moment of inertia of the body $i$ relative to its center of mass.
Example: Eight bars¶
Let's compute the moment of inertia of the set of eight equal and homogeneous bars depicted in the figure below relative to its center of mass.
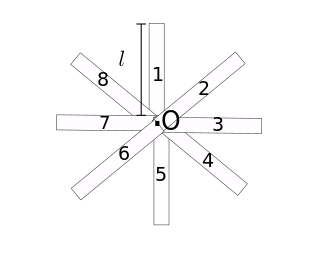
By symmetry, the center of mass of this system is in the point $O$. So, to compute the moment of inertia relative to this point, we must use the parallel axis theorem to each bar, and then sum the results, as in Eq.(\ref{eq:paral}).
\begin{equation} \begin{array}{l} I^{cm}_{zz}={} & I^{cm1}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm2}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm3}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm4}_{zz}+m\left(\frac{l}{2}\right)^2 + \\ & I^{cm5}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm6}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm7}_{zz}+m\left(\frac{l}{2}\right)^2+I^{cm8}_{zz}+m\left(\frac{l}{2}\right)^2 \label{} \end{array} \end{equation}The moment of inertia of a bar relative to its center of mass is $\frac{ml^2}{12}$.
So the moment of inertia of the system relative to its center of mass is:
Verify that for this example, we also could have explored even more the symmetry of the system and computed the total moment of inertia as the sum of the moment of inertia of four bars, each with length $2l$ and mass $2m$, each rotating around its center.
Matrix of Inertia¶
Let's find the expression for the moment of inertia of a three-dimensional problem for a system rotating around an axis where we can't reduce the problem to a possible planar rotation. But let's continue considering that the axis of rotation passes through the center of mass (one can always use the theorem of parallel axis).
In this case, the angular momentum for a system composed of a set of particles is:
\begin{equation} \begin{array}{l} \vec{H}_{cm} &= \sum \vec{r}_{i/cm} \times \vec{p}_i \\ &= \sum \vec{r}_{i/cm} \times m_i\vec{v}_i \\ &= \sum \vec{r}_{i/cm} \times m_i(\vec{\omega}_i \times \vec{r}_{i/cm}) \\ \vec{H}_{cm} &= \sum m_i (\vec{r}_{i/cm} \times (\vec{\omega}_i \times \vec{r}_{i/cm})) \label{} \end{array} \end{equation}Calculating the vector triple product (mnemonic: abc = bac - cab) and separating the terms for each component of the angular momentum:
\begin{equation} \begin{array}{r} H_{x/cm} &=& \sum m_i \big(&(y_i^2+z_i^2)\omega_x &-x_iy_i\omega_y &-x_iz_i\omega_z \big) \\ H_{y/cm} &=& \sum m_i \big(&-y_ix_i\omega_x &(z_i^2+x_i^2)\omega_y &-y_iz_i\omega_z \big) \\ H_{z/cm} &=& \sum m_i \big(&-z_ix_i\omega_x &-z_iy_i\omega_y &(x_i^2+y_i^2)\omega_z \big) \end{array} \label{} \end{equation}Once again, in analogy to the linear momentum, we can write the equation above as $\vec{H}_{cm} = I_{cm} \vec{w}$, which in matrix form is:
\begin{equation} \begin{bmatrix} H_x \\ H_y \\ H_z \end{bmatrix} = \begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zx} & I_{zz} \end{bmatrix} \cdot \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \label{} \end{equation}The matrix with the moment of inertia terms in the equation above is referred as the matrix of inertia (or inertia matrix or inertia tensor):
\begin{equation} I^{cm} = \begin{bmatrix} &\sum m_i (y_i^2+z_i^2) &-\sum m_i x_iy_i &-\sum m_i x_iz_i \\ &-\sum m_i y_ix_i &\sum m_i (z_i^2+x_i^2) &-\sum m_i y_iz_i \\ &-\sum m_i z_ix_i &-\sum m_i z_iy_i &\sum m_i (x_i^2+y_i^2) \end{bmatrix} \label{} \end{equation}Equivalently, for a rigid body the matrix of inertia is:
\begin{equation} I^{cm} = \begin{bmatrix} &\int (y^2+z^2)\,\mathrm d m &-\int xy\,\mathrm d m &-\int xz\,\mathrm d m \\ &-\int yx\,\mathrm d m &\int (z^2+x^2)\,\mathrm d m &-\int yz\,\mathrm d m \\ &-\int zx\,\mathrm d m &-\int zy\,\mathrm d m &\int (x^2+y^2)\,\mathrm d m \end{bmatrix} \label{} \end{equation}It's usual to refer to the matrix of inertia simply by:
\begin{equation} I^{cm} = \begin{bmatrix} I_{xx} & I_{xy} & I_{xz} \\ I_{yx} & I_{yy} & I_{yz} \\ I_{zx} & I_{zx} & I_{zz} \end{bmatrix} \label{} \end{equation}Note that in the notation of subscripts with two axes, the first subscript refers to the component (axis) of the angular momentum, and the second subscript refers to the component (axis) of the angular velocity.
Principal axes¶
If the axes of rotation to calculate the moment of inertia are aligned with the axes of symmetry of the body passing through the center of mass (referred as principal axes), the terms off the main diagonal of the matrix of inertia are all zero because, by definition of center of mass, the mass is equally distributed around these axes of symmetry for each pair of coordinates considered in the integration. The terms off-diagonal are called product of inertia. In this case, the matrix of inertia becomes:
\begin{equation} I^{cm} = \begin{bmatrix} I_1 & 0 & 0 \\ 0 & I_2 & 0 \\ 0 & 0 & I_3 \end{bmatrix} \label{} \end{equation}where $I_1$, $I_2$ and $I_3$ are the moments of inertia around each of the principal axes of the body.
This is a common strategy employed in biomechanics; in motion analysis we construct a base for each segment such that this base is aligned to the principal axes of the segment, and we do that for every instant the segment moves.
Example: Cylinder¶
Consider a cylinder with constant density shown in the figure below and compute the moment of inertia around the three axes relative to the center of mass.
The mass of this cylinder is $m = \rho h \pi R^2$ and, by symmetry, the moment of inertia is in the center (centroid) of the cylinder.

The easiest approach to this problem is to use cylindrical coordinates $\theta, r, z$. In the integrals, the differential term $\mathrm d m$ will be replaced by $\rho r \,\mathrm d \theta\,\mathrm d r\,\mathrm d z$ and the limits of the integral will be $[0,2\pi]$, $[0,R]$, $[-h/2,h/2]$.
First, around the $z$ axis:
\begin{equation} \begin{array}{l} I_{zz}^{cm} &= \int\limits_B (x_{/cm}^2+y_{/cm}^2)\,\mathrm d m \\ &= \int\limits_{-h/2}^{h/2}\int\limits_0^R\int\limits_0^{2\pi} r^2 \rho r \,\mathrm d \theta\,\mathrm d r\,\mathrm d z \\ &= \rho \int\limits_{-h/2}^{h/2}\int\limits_0^R\int\limits_0^{2\pi} r^3 \,\mathrm d \theta\,\mathrm d r\,\mathrm d z \\ &= \rho \int\limits_{-h/2}^{h/2}\int\limits_0^R 2\pi r^3 \,\mathrm d r\,\mathrm d z \\ &= \rho \int\limits_{-h/2}^{h/2} 2\pi \frac{R^4}{4} \,dz \\ &= \rho \pi \frac{R^4}{2}h \\ I_{zz}^{cm} &= \dfrac{mR^2}{2} \label{} \end{array} \end{equation}Now, around the $x$ axis:
\begin{equation} \begin{array}{l} I_{xx}^{cm} &= \int\limits_B (z_{/cm}^2+y_{/cm}^2)\,\mathrm d m \\ &= \int\limits_{-h/2}^{h/2}\int\limits_0^R\int\limits_0^{2\pi} (z^2+r^2\sin^2(\theta)) \rho r \,\mathrm d \theta\,\mathrm d r\,\mathrm d z \\ I_{xx}^{cm} &= \rho\int\limits_{-h/2}^{h/2}\int\limits_0^R\int\limits_0^{2\pi} (r z^2+r^3\sin^2(\theta)) \,\mathrm d \theta\,\mathrm d r\,\mathrm d z \label{} \end{array} \end{equation}And by symmetry, the moment of inertia around the axis $y$ passing by the center of mass is equal to the moment of inertia around the axis $x$.
We will solve this integral using the Sympy library:
# define variables
h, R, rho, m1 = sym.symbols('h, R, rho, m', positive=True)
theta, r, z = sym.symbols('theta, r, z')
m = rho*h*sym.pi*R**2
# solve the integral
Ixx = rho*sym.integrate(sym.integrate(sym.integrate(r*z**2 + (r**3)*sym.sin(theta)**2,
(theta, 0, 2*sym.pi)),
(r, 0, R)),
(z, -h/2, h/2))/m
Ixxcm = sym.simplify(m1*Ixx)
print2('I^{cm}_{xx}=I^{cm}_{yy}', Ixxcm)
The product of inertia terms
By inspecting the problem, we know that because of symmetry of the axes w.r.t. the cylinder, the product of inertia terms of the matrix of inertia should be all zero. Let's confirm that.
Here are the integrals:
The product of inertia terms are indeed all zero.
The parallel axis theorem for rigid bodies in three dimensions¶
The parallel axis theorem for rigid bodies in three dimensions is (see page 1083 of Ruina and Pratap, (2019)):
\begin{equation} \begin{array}{l} I^O = I^{cm} + m\begin{bmatrix} & y_{cm/O}^2+z_{cm/O}^2 &-x_{cm/O}y_{cm/O} &-x_{cm/O}z_{cm/O} \\ &-y_{cm/O}x_{cm/O} & z_{cm/O}^2+x_{cm/O}^2 &-y_{cm/O}z_{cm/O} \\ &-z_{cm/O}x_{cm/O} &-z_{cm/O}y_{cm/O} & x_{cm/O}^2+y_{cm/O}^2 \end{bmatrix} \label{} \end{array} \end{equation}where $x_{cm/O}, y_{cm/O}, z_{cm/O}$ are the $x, y, z$ coordinates of the center of mass with respect to a coordinate system whose origin is located at point $O$.
The terms $I^O_{i,j}$ of the inertia tensor above can be represented in a shorter form as:
\begin{equation} \begin{array}{l} I^O_{ij} = I^{cm}_{ij} + m\left(|\vec{r}_{cm/O}|^2\delta_{ij} - r_{i,cm/O}r_{j,cm/O}\right) \label{} \end{array} \end{equation}where $\vec{r}_{cm/O} = x_{cm/O} \hat{i} + y_{cm/O}\hat{j} + z_{cm/O}\hat{k}$, $\delta_{ij}$ is the Kronecker delta, and $i,j$ varies from 1 to 3 (which also span the $x, y, z$ coordinates).
Moment of rotational inertia and area moment of inertia¶
Another related quantity to moment of rotational inertia is the area moment of inertia; the latter is more used in the field of strength of materials. The area moment of inertia is a property of the shape of a body, it expresses the difficulty to deflect, bend or stress this body, and is given by:
\begin{equation} \begin{array}{l} I = \int\limits r^2\,\mathrm d A \label{} \end{array} \end{equation}where $\mathrm d A$ is the differential of area.
One can see that the area moment of inertia has no mass term; it has dimension $[L]^4$ and SI unit $m^4$.
To salient the difference between these two quantities, the moment of rotational inertia is also known as mass moment of inertia.
Further reading¶
- Center of mass: Read pages pages 145-160 of the Ruina and Pratap (2019);
- Moment of inertia: Read pages 771-781 and 1081-1089 of the Ruina and Pratap (2019), read the chapter 17 of the Hibbeler's book (available in the Classroom).
Video lectures on the internet¶
- Center of mass:
- Khan Academy: definition, definição (in Portuguese);
- MIT OpenCourseWare: definition, of three objects, of a continuous system, of extended objects, of a uniform rod;
- Moment of inertia:
- Khan Academy: definition, definição (in Portuguese);
- MIT OpenCourseWare: definition, of a rod, of a disc, parallel axis theorem, of a sphere, matrix of inertia;
- Difference between mass and area moments of inertia.
Problems¶
- Solve problems 2.2.5, 2.2.7, 16.3.11, 16.3.15 from Ruina and Pratap (2019).
- Determine the center of mass position and moment of inertia (around the principal axes of the object) for (adopt mass equal 1 kg):
- A planar disc with radius $r$.
- A planar square with side $a$.
- A planar ellipse with semi-axes $a$ and $b$.
- A sphere with radius $r$.
- A cube with side $a$.
- An ellipsoid with semi-axes $a$, $b$ and $c$ (see http://scienceworld.wolfram.com/physics/MomentofInertiaEllipsoid.html).
- Calculate the matrix of inertia for the following systems:
- A particle with mass 1 kg located at $[1, 2, 0]\,m$ in relation to the origin $[0, 0, 0]\,m$.
- A set of two particles, each with mass 1 kg, located at $[1, 2, 0]\,m$ and $[-1, -2, 0]\,m$ in relation to the set center of mass.
- Check examples 17.1 e 17.2 from Hibbeler's book.
References¶
- Ruina A, Rudra P (2019) Introduction to Statics and Dynamics. Oxford University Press.
- R. C. Hibbeler (2010) Engineering Mechanics Dynamics. 12th Edition. Pearson Prentice Hall.