Introdução aos testes de hipóteses¶
Reginaldo K Fukuchi¶
Com frequência lemos em artigos científicos descrições de natureza similar a esta.
“With a two-tailed t-test, the null hypothesis was rejected at the 5% alpha-level. The results were statistically significant with a p-value of 0.018”
Hoje iremos apresentar conceitos sobre o teste de hipótese. O teste de hipótese é um teste estatístico que usa dados obtidos de uma amostra para tomar decisões a respeito de aceitar ou não a hipótese nula ($H_0$).
Embora estamos tratanto de estatística, podemos considerar esta tomada de decisão como a mesma decisão que um juiz deve tomar ao condenar ou absolver um réu. Esta decisão é baseada nas evidências apresentadas. Tipicamente, pressupomos que todos somos inocentes até que provem o contrário. Na estatística, também tipicamente assumimos, pelo menos temporariamente, que a $H_0$ é verdadeira. Então com base nas evidências decidimos rejeitá-la ou não em favor da hipótese alternativa ($H_1$).
Portanto,
- $H_0$ consiste declarar estatisticamente que não existe diferença, resposta ou mudança.
- $H_1$ consiste em contradizer a $H_0$
Por exemplo, uma suposição é feita sobre uma determinada característica da população que pode ou não ser verdadeira. Então, tudo se inicia com uma boa pergunta. Exemplos:
- A renda média do brasileiro diminiu em relação ao ano passado?
- A média de temperatura caiu em relação ao inverno do ano passado?
- A proporção de mulheres matriculadas aumentou?
Para responder estas e outras questões recorremos então aos testes estatísticos.
A melhor forma de estudar os testes de hipóteses é por meio de exemplos. Então vamos usar alguns exemplos de (Bluman, 2012).
Teste Z para uma amostra¶
Example. A researcher claims that the average cost of men’s athletic shoes is less than 80 dollars. He selects a random sample of 36 pairs of shoes from a catalog and finds the following costs (in dollars). (The costs have been rounded to the nearest dollar.) Is there enough evidence to support the researcher’s claim at a $\alpha=$ 0.10? Assume $\sigma=$ 19.2.
Baseado na descrição do problema acima, podemos notar que o desvio padrão da população ($\sigma=$) é conhecido e que o tamanho da amostra (n > 30). Então podemos usar o teste Z para responder esta questão.
Ainda que existam particularidades, a formulação geral de um teste estatístico segue a seguinte convenção.
$$\mathbf{Teste} = \frac{\mathbf{Observado} - \mathbf{Esperado}}{\mathbf{Erro Padrão}} $$Para o teste Z, podemos formular assim.
$$\mathbf{Z} = \frac{\mathbf{\bar{X}} - \mathbf{\mu}}{\frac{\mathbf{\sigma}}{\mathbf{\sqrt{n}}}} $$Onde,
$\mathbf{\bar{X}}$: média da amostra
$\mathbf{\mu}$: média da população
$\mathbf{\sigma}$: desvio padrão da população
n: tamanho da amostra
Antes de resolver este problema, precisamos formular as $H_0$ e $H_1$. Vejamos que a palavra "less" foi mencionada. Então, $H_1$ é unicaudal e portanto.
$$ \mathbf{H_0} : \mathbf{\mu} = 80$$$$\mathbf{H_1} : \mathbf{\mu} < 80$$
Perceba que se a palavra different fosse usada no lugar de less, as hipóteses seriam.
$$ \mathbf{H_0} : \mathbf{\mu} = 80$$$$\mathbf{H_1} : \mathbf{\mu} \neq 80$$
Portanto, existem diferentes frases que são usadas para expressar as hipóteses do estudo como mostra a Figura abaixo.

Outra informação importante descrita no problema foi $\alpha$ = 0.10 que é considerado o nível de significância do teste estatístico. O nível de significância é a probabilidade de rejeitar $H_0$ quando ela é verdadeira que também é conhecido como erro tipo I. O valor $\alpha$ = 0.05 tem sido adotado pela comunidade científica e sua origem se deveu ao fato que Ronald Fisher considerava conveniente uma probabilidade de 1 em 20 de rejeitar erroneamente a $H_0$.
Assim, como um juiz pode culpar um inocente também corremos o risco de rejeitar uma $H_0$ verdadeira (erro tipo I). Ao mesmo tempo, podemos também aceitar (ou não rejeitar) uma $H_0$ quando ela não é verdadeira. Neste útimo caso estamos cometendo o erro tipo II. De fato existem quatro possibilidades (duas decisões corretas e duas incorretas) quando tomamos uma decisão baseado no teste estatístico como ilustra a Figura abaixo.
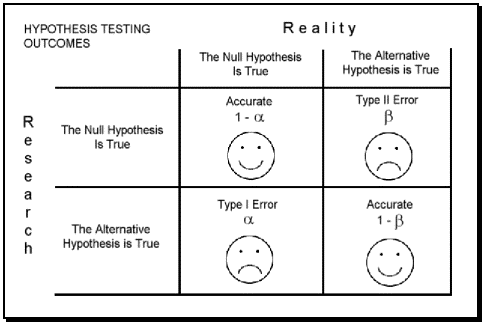
Agora que entedemos algumas questões fundamentais podemos resolver o problema original. Vamos usar o R para isto.
# Import the necessary libraries
library("psych")
# Raw data
shoePrices <- c(60,70,75,55,80,55,50,40,80,70,50,95,120,90,75,85,80,60,110,65,80,85,85,45,75,60,90,90,60,95,110,85,45,90,70,70)
mu <- 80 # population mean
sPricesM <- mean(shoePrices) # Mean shoe prices
sigma <- 19.2 # population SD
alpha <- 0.10 # level of significance
n <- 36 # sample size
# Z test
ztest <- (sPricesM - mu)/(sigma/sqrt(n))
ztest
# Finding critical value for alpha = 0.05 two-tailed test
cv <- qnorm(alpha, mean = 0, sd = 1, lower.tail = TRUE)
cv
Como a hipótese foi direcional, vamos usar o teste unicaudal. Como o valor do teste é menor que o valor crítico, a hipótese nula pode ser rejeitada. Portanto, podemos concluir que existe evidência suficiente para indicar que o custo médio de um calçado é menor que U$80.
Dependendo da formulação da hipótese estatística, o teste estatístico pode ser unicaudal ou bicaudal. O teste unicaudal é aquele onde a região de rejeição só pode estar a direita (maior) ou a esquerda da média (menor). Por outro lado o bicaudal a região de rejeição pode se encontrar em qualquer lado ($\neq$) da média. Portanto, a hipótese deve ser formulada antes de ter acesso aos dados do estudo. A figura abaixo ilustra as diferentes condições de teste.

Teste t para uma amostra¶
Veja a descrição de um outro problema sobre infecções hospitalares (Bluman, 2012).
"A medical investigation claims that the average number of infections per week at a hospital in southwestern Pennsylvania is 16.3. A random sample of 10 weeks had a mean number of 17.7 infections. The sample standard deviation is 1.8. Is there enough evidence to reject the investigator’s claim at $\alpha$ = 0.05?"
De acordo com a descrição podemos notar que:
- o tamanho da amostra é pequena (n=10)
- o desvio padrão da população ($\sigma$) é desconhecido
Vimos anteriormente que para as condições acima, não é recomendado usar a distribuição Z mas sim uma outra família chamada distribuição t de Student. Portanto, para resolver este problema vamos usar o teste t com a seguinte formulação.
$$\mathbf{t} = \frac{\mathbf{\bar{X}} - \mathbf{\mu}}{\frac{\mathbf{s}}{\mathbf{\sqrt{n}}}} $$Onde,
$\mathbf{\bar{X}}$: média da amostra
$\mathbf{\mu}$: média da população
$\mathbf{s}$: desvio padrão da amostra
n: tamanho da amostra
g.l.: graus de liberdade (n-1)
De acordo com o problema as seguintes hipóteses são formuladas: $$ \mathbf{H_0} : \mathbf{\mu} = 16.3$$ $$\mathbf{H_1} : \mathbf{\mu} \neq 16.3$$
Portanto, o teste é bicaudal.
# presented data
mu <- 16.3 # avg population
x <- 17.7 # avg sample
s <- 1.8 # sd sample
n <- 10 # sample size
df <- n-1 # dof
alpha <- 0.05
# t test
ttest <- (x - mu)/(s/sqrt(n))
round(ttest,3)
cv <- qt(alpha/2, df)
round(cv*c(1,-1),3) # critical values
- -2.262
- 2.262
Como o valor do teste é maior que o valor crítico, rejeita-se $H_0$. Portanto, conclui-se que o número médio de infecções hospitalares por semana é diferente da suspeitada.
Comparação entre duas médias com teste Z¶
Em alguns casos (para não dizer a maioria) estamos interessados em comparar duas amostras como por exemplo um grupo que fez tratamento e o outro controle.
De novo vamos usar um exemplo do livro.
"A survey found that the average hotel room rate in New Orleans is $ 88.42 and the average room rate in Phoenix is $ 80.61. Assume that the data were obtained from two samples of 50 hotels each and that the standard deviations of the populations are $ 5.62 and $ 4.83, respectively. At $\alpha$ =0.05, can it be concluded that there is a significant difference in the rates?"
Considerando que ambas as amostras sejam aleatórias, independentes e que o desvio padrão da população, das quais elas pertencem, seja conhecido podemos usar o teste Z. Note também que o tamanho da amostra é maior que 30.
Mas agora temos duas amostras e precisamos formular as hipóteses um pouco diferente das que foram feitas anteriormente como segue.
$$ \mathbf{H_0} : \mathbf{\mu_1} = \mathbf{\mu_2}$$$$\mathbf{H_1} : \mathbf{\mu_1} \neq \mathbf{\mu_2}$$
Ou, alternativamente
$$ \mathbf{H_0} : \mathbf{\mu_1} - \mathbf{\mu_2} = 0$$$$\mathbf{H_1} : \mathbf{\mu_1} - \mathbf{\mu_2} \neq 0$$
Então, a distribuição agora será de diferenças entre as médias de pares de amostras retiradas da população. Se as populações tiverem médias iguais, esta média das médias das diferenças também será zero. A variância da diferença $\bar{X_1} - \bar{X_2}$ é igual a soma das variâncias individuais,
$$ \mathbf{\sigma^2}_{\bar{X_1} - \bar{X_2}} = \sigma^2_{\bar{X}_1} + \sigma^2_{\bar{X}_2} $$E então,
$$ \mathbf{\sigma^2}_{\bar{X_1} - \bar{X_2}} = \frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}$$portanto, o erro padrão da diferença $\bar{X_1} - \bar{X_2}$ é
$$ \mathbf{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}} $$Então, o teste Z para comparação entre amostras quando o desvio padrão da população é conhecido é calculado por
$$ \mathbf{z} = \frac{(\mathbf{\bar{X}_1} - \mathbf{\bar{X}_2}) - (\mathbf{\mu_1} - \mathbf{\mu}_2)}{\mathbf{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}}} $$Resolvemos então o problema apresentado anteriormente no R.
# Presented data
x1 <- 88.42 # avg sample 1
x2 <- 80.61 # avg sample 2
sigma1 <- 5.62 # sd population 1
sigma2 <- 4.83 # sd population 2
n1 <- 50 # sample size 1
n2 <- n1 # sample size 2
alpha <- 0.05 # sig. level
# Calculating Z test
ztest <- ((x1-x2) - 0) / sqrt((sigma1^2/n1) + (sigma2^2/n2))
round(ztest,3)
# Finding critical value for two-tailed test
cv <- qnorm(alpha/2, mean=0, sd = 1)
round(cv*c(1,-1),3)
- -1.96
- 1.96
Como o teste estatítico é maior que o valor crítico podemos rejeitar $H_0$ em favor da $H_1$ e concluir que as diárias dos hotéis nas duas cidades são diferentes. Note que não foi dado uma hipótese direcional.
Comparação entre duas médias com teste t¶
Amostras independentes¶
Na maioria dos casos vamos nos deparar com situações onde o desvio padrão das populações estudadas é desconhecido e apenas o das amostras pode ser obtido. Em adição, as amostras obtidas também são inferiores a 30. Nestes casos não podemos usar o teste Z pois violaremos as suas pressuposições. Vamos analisar o exemplo abaixo do livro.
"The average size of a farm in Indiana County, Pennsylvania, is 191 acres. The average size of a farm in Greene County, Pennsylvania, is 199 acres. Assume the data were obtained from two samples with standard deviations of 38 and 12 acres, respectively, and sample sizes of 8 and 10, respectively. Can it be concluded at $\alpha$ = 0.05 that the average size of the farms in the two counties is different? Assume the populations are normally distributed."
Como pode ser observado, os desvios padrões das populações não foram informados e o tamanho da amostra é pequeno. Vimos anteriormente que a família de distribuição t pode ser usado nestes casos pois o formato da distribuição varia em função do tamanho da amostra.
A formulação do teste t para comparação de duas médias amostrais é similar ao do teste Z como segue.
$$ \mathit{t} = \frac{(\mathbf{\bar{X}_1} - \mathbf{\bar{X}_2}) - (\mathbf{\mu_1} - \mathbf{\mu}_2)}{\mathbf{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}}} $$Note que a diferença foi o uso do desvio padrão das amostras. Se você recordar, para a distribuição t é necessário levar em conta o grau de liberdade (g.l. = n-1). No caso, como temos um tamanho de amostra diferente usamos o menor para ser conservador.
É importante lembrar sempre de forumlar as hipóteses antes de realizar o teste estatítico. Para este caso, não houve informação de direção e consideramos hipótese bidirecional.
$$ \mathbf{H_0} : \mathbf{\mu_1} - \mathbf{\mu_2} = 0$$$$\mathbf{H_1} : \mathbf{\mu_1} - \mathbf{\mu_2} \neq 0$$
# Presented data
x1 <- 191
x2 <- 199
n1 <- 8
n2 <- 10
s1 <- 38
s2 <- 12
alpha <- 0.05
df1 <- n1-1
df2 <- n2-1
# Performing t test
ttest <- ((x1-x2) - 0) / sqrt((s1^2/n1) + (s2^2/n2))
round(ttest,3)
# Calculating critical value
if (df1 < df2) {df <- df1} else {df <- df2}
cv <- qt(alpha/2,df)
round(cv*c(1,-1),3)
- -2.365
- 2.365
Como o valor do teste estatístico está dentro da região de aceitação, não existe evidência suficiente para rejeitar a $H_0$. Portanto, podemos concluir que não existe diferença na dimensão das fazendas dos dois condados.
Amostras dependentes¶
Em algumas situações, é de interesse que a mesma amostra seja comparada em dois instantes (antes e depois) como por exemplo para testar o efeito de uma intervenção. Nestes casos, não podemos considerar valores independentes. Considere o seguinte exemplo abaixo retirado do livro.
"A dietitian wishes to see if a person’s cholesterol level will change if the diet is supplemented by a certain mineral. Six subjects were pretested, and then they took the mineral supplement for a 6-week period. The results are shown in the table. (Cholesterol level is measured in milligrams per deciliter.) Can it be concluded that the cholesterol level has been changed at $\alpha$ = 0.10? Assume the variable is approximately normally distributed."
Perceba no exemplo que as medidas foram obtidas da mesma amostra de sujeito e, portanto, são dependentes. A formulação das hipóteses segue o mesmo princípio que anteriormente.
$$ \mathbf{H_0} : \mathbf{X_{pre}} - \mathbf{X_{pos}} = 0$$$$\mathbf{H_1} : \mathbf{X_{pre}} - \mathbf{X_{pos}} \neq 0$$
Se considerarmos que $\bar{D} = \mathbf{X_{pre}} - \mathbf{X_{pos}}$, então a formulação do teste estatístico para condições dependentes é,
$$ \mathbf{t} = \frac{\mathbf{\bar{D}} - \mathbf{\mu_D}}{\frac{\mathbf{s_D}}{\sqrt{n}}} $$Onde, $S_D$ é o desvio padrão das diferenças e o d.f. = n - 1.
Vamos resolver o problema no R.
# Raw data
prior <- c(210,235,208,190,172,244)
after <- c(190,170,210,188,173,228)
n <- 6 # sample size
df <- n-1 # dof
alpha <- 0.1 # sig level
# Calculated data
dM <- mean(prior-after) # avg of differences
sD <- sd(prior-after) # sd of differences
# Statistical test
ttest <- (dM - 0)/(sD/sqrt(n))
round(ttest,3)
# Critical value
cv <- qt(alpha/2,df)
round(cv*c(1,-1),3)
- -2.015
- 2.015
Como o valor do teste está dentro da região de aceitação, não existe evidência para refutar a $H_0$ em favor de $H_1$ e, portanto, conclui-se que os níveis de colesterol não mudaram em função da dieta. Veja se o desenho do estudo permite tirar esta conclusão.
Poder estatístico¶


Referências¶
- Bluman, Allan G. Elementary statistics : a step by step approach / Allan Bluman. — 8th ed.
- Krzywinski & Altman (2013). Points of significance: Power and sample size. Nature Methods 10, 1139–1140.