To build these slides:

In [70]:
%%bash
jupyter nbconvert \
    --to=slides \
    --reveal-prefix=https://cdnjs.cloudflare.com/ajax/libs/reveal.js/3.2.0/ \
    --output=dataphilly-jul2016 \
    ./DataPhilly\ July\ 2016\ Introduction\ to\ Probabilistic\ Programming.ipynb

[NbConvertApp] Converting notebook ./DataPhilly July 2016 Introduction to Probabilistic Programming.ipynb to slides
[NbConvertApp] Writing 561178 bytes to ./dataphilly-jul2016.slides.html
In [1]:
%matplotlib inline
In [2]:
from __future__ import division
In [3]:
from IPython.display import Image
In [4]:
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
from theano import tensor as T
In [5]:
blue, green, red, purple, gold, teal = sns.color_palette()
In [6]:
plt.rc('figure', figsize=(8, 6))

LABELSIZE = 14
plt.rc('axes', labelsize=LABELSIZE)
plt.rc('legend', fontsize=LABELSIZE)
plt.rc('xtick', labelsize=LABELSIZE)
plt.rc('ytick', labelsize=LABELSIZE)
In [7]:
SEED = 2285280 # from random.org

Introduction to Probabilistic Programming

DataPhilly

July 13, 2016

@Austin Rochford ([email protected])

Probabilistic Programming

  • Programming with random variables
  • User specifies a generative model for the observed data
    • "Tell the story" of how the data were created
  • The language runtime/software library automatically performs inference

What do we mean by inference?

  • Maximum likelihood inference
  • Maxumum a posteriori inference
  • Full posterior inference

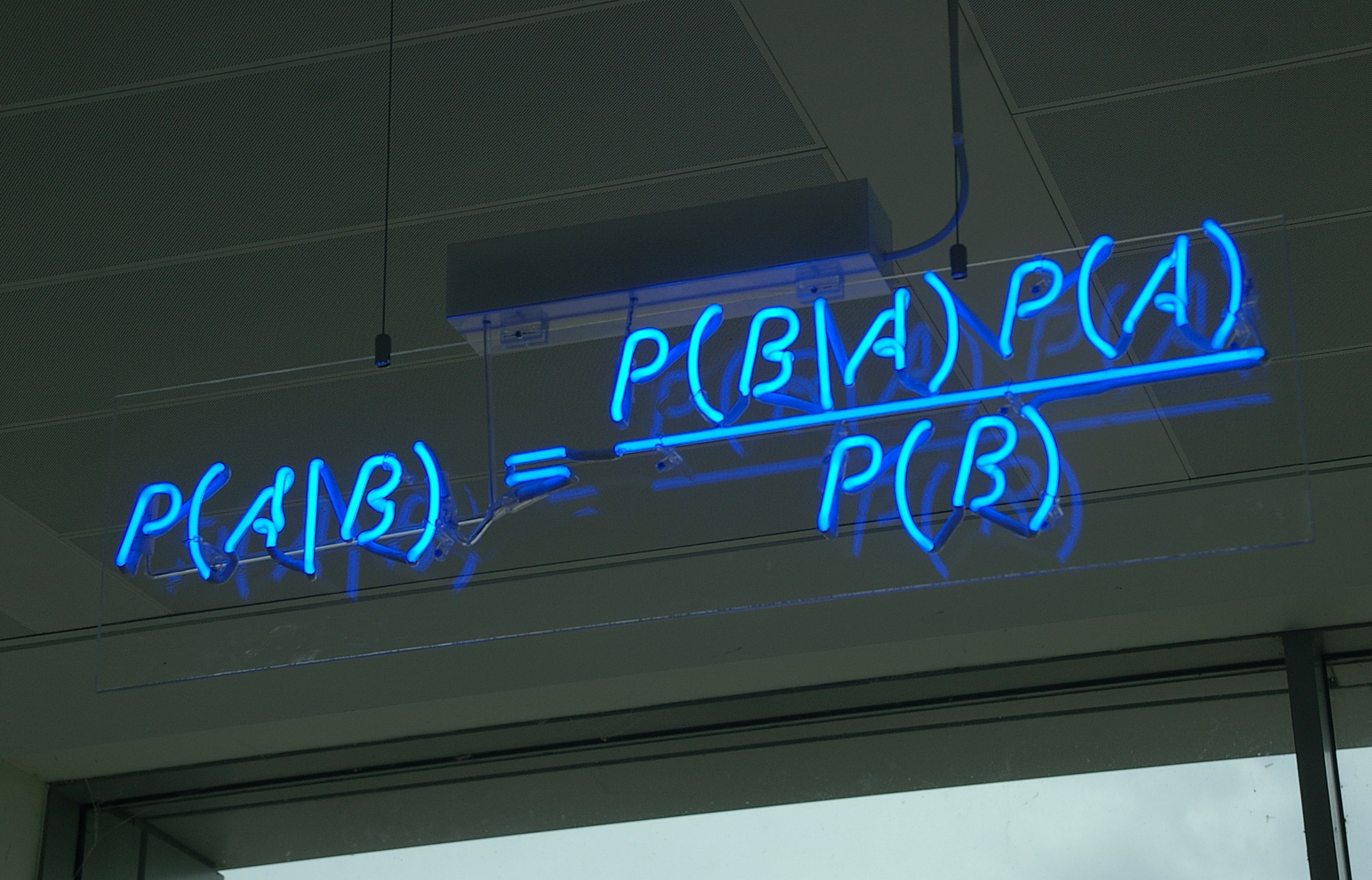
Disease Testing

A certain rare disease affects one in 10,000 people. A test for the disease gives the correct result 99.9% of the time.

What is the probability that a given test is positive?

In [8]:
import pymc3 as pm

with pm.Model() as pretest_disease_model:
    # This is our prior belief about whether or not the subject has the disease,
    # given its prevalence of the disease in the general population
    has_disease = pm.Bernoulli('has_disease', 1e-4)
    
    # This is the probability of a positive test given the presence or lack
    # of the disease
    p_positive = pm.Deterministic('p_positive',
                                  T.switch(T.eq(has_disease, 1),
                                           # If the subject has the disease,
                                           # this is the probability that the
                                           # test is positive
                                           0.999,
                                           # If the subject does not have the
                                           # disease, this is the probability
                                           # that the test is negative
                                           1 - 0.999))
    
    # This is the observed test result
    test_positive = pm.Bernoulli('test_positive', p_positive)
In [9]:
samples = 40000
In [10]:
with pretest_disease_model:
    step = pm.Metropolis()
    pretest_disease_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 40000 of 40000 complete in 6.1 sec
In [11]:
pretest_disease_trace['test_positive']
Out[11]:
array([0, 0, 0, ..., 0, 0, 0])
In [12]:
pretest_disease_trace['test_positive'].size
Out[12]:
40000

The probability that a given test is positive is

In [13]:
pretest_disease_trace['test_positive'].mean()
Out[13]:
0.001575
$$ \begin{align*} P(\textrm{Test } +) = &\ P(\textrm{Test } +\ |\ \textrm{Disease}) P(\textrm{Disease}) \\ & + P(\textrm{Test } +\ |\ \textrm{No disease}) P(\textrm{No disease}) \end{align*} $$
In [14]:
0.999 * 1e-4  + (1 - 0.999) * (1 - 1e-4)
Out[14]:
0.0010998000000000008

If a subject tests positive, what is the probability they have the disease?

In [15]:
with pm.Model() as disease_model:
    # This is our prior belief about whether or not the subject has the disease,
    # given its prevalence of the disease in the general population
    has_disease = pm.Bernoulli('has_disease', 1e-4)
    
    # This is the probability of a positive test given the presence or lack
    # of the disease
    p_positive = pm.Deterministic('p_positive',
                                  T.switch(T.eq(has_disease, 1),
                                           # If the subject has the disease,
                                           # this is the probability that the
                                           # test is positive
                                           0.999,
                                           # If the subject does not have the
                                           # disease, this is the probability
                                           # that the test is negative
                                           1 - 0.999))
    
    # This is the observed positive test
    test_positive = pm.Bernoulli('test_positive', p_positive, observed=1)
In [16]:
with disease_model:
    step = pm.Metropolis()
    disease_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 40000 of 40000 complete in 3.8 sec

The probability that someone who tests positive for the disease has it is

In [17]:
disease_trace['has_disease'].mean()
Out[17]:
0.096775
$$ \begin{align*} P(\textrm{Disease}\ |\ \textrm{Test }+) & = \frac{P(\textrm{Test }+\ |\ \textrm{Disease}) P(\textrm{Disease})}{P(\textrm{Test }+)} \end{align*} $$
In [18]:
0.999 * 1e-4 / (0.999 * 1e-4 + (1 - 0.999) * (1 - 1e-4))
Out[18]:
0.09083469721767587

The Monty Hall Problem

If we select the first door and Monty opens the third to reveal a goat, should we change doors?

In [19]:
with pm.Model() as monty_model:
    # We have no idea where the prize is at the beginning
    prize = pm.DiscreteUniform('prize', 0, 2)
    
    # The probability that Monty opens each door
    p_open = pm.Deterministic('p_open',
                              T.switch(T.eq(prize, 0), 
                                       # If the prize is behind the first door,
                                       # he chooses to open one of the others
                                       # at random
                                       np.array([0., 0.5, 0.5]),
                                       T.switch(T.eq(prize, 1),
                                                # If it is behind the second door,
                                                # he must open the third door
                                                np.array([0., 0., 1.]),
                                                # If it is behind the third door,
                                                # he must open the second door
                                                np.array([0., 1., 0.]))))
    
    # Monty opened the third door, revealing a goat
    opened = pm.Categorical('opened', p_open, observed=2)
In [20]:
samples = 10000
In [21]:
with monty_model:
    step = pm.Metropolis()
    monty_trace = pm.sample(samples, step, random_seed=SEED)
    
monty_trace_df = pm.trace_to_dataframe(monty_trace)

 [-----------------100%-----------------] 10000 of 10000 complete in 1.4 sec
In [22]:
monty_trace_df.head()
Out[22]:
p_open__0 p_open__1 p_open__2 prize
0 0.0 0.0 1.0 1
1 0.0 0.5 0.5 0
2 0.0 0.0 1.0 1
3 0.0 0.0 1.0 1
4 0.0 0.0 1.0 1
In [23]:
(monty_trace_df.groupby('prize')
               .size()
               .div(monty_trace_df.shape[0]))
Out[23]:
prize
0    0.3196
1    0.6804
dtype: float64

PyMC3

PyMC3 is a python module for Bayesian statistical modeling and model fitting which focuses on advanced Markov chain Monte Carlo fitting algorithms. Its flexibility and extensibility make it applicable to a large suite of problems.

Built on top of theano

A/B Testing

Suppose variant A sees 510 visitors and 40 purchases, but variant B sees 505 visitors and 50 conversions.

In [24]:
with pm.Model() as ab_model:
    # A priori, we have no idea what the purchase rate for variant A will be
    a_rate = pm.Uniform('a_rate')
    # We observed 40 purchases from 510 visitors who saw variant A
    a_purchases = pm.Binomial('a_purchases', 510, a_rate, observed=40)
    
    # A priori, we have no idea what the purchase rate for variant B will be
    b_rate = pm.Uniform('b_rate')
    # We observed 40 purchases from 510 visitors who saw variant A
    b_purchases = pm.Binomial('b_purchases', 505, b_rate, observed=45)

Applied interval-transform to a_rate and added transformed a_rate_interval to model.
Applied interval-transform to b_rate and added transformed b_rate_interval to model.
In [25]:
samples = 10000
In [26]:
with ab_model:
    step = pm.NUTS()
    ab_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 10000 of 10000 complete in 3.2 sec
In [27]:
fig, ax = plt.subplots(figsize=(8, 6))

BINS = 30

ax.hist(np.clip(ab_trace['a_rate'], 0.03, 0.15),
        bins=BINS, normed=True, lw=0, alpha=0.75,
        label="Variant A");
ax.hist(np.clip(ab_trace['b_rate'], 0.03, 0.15),
        bins=BINS, normed=True, lw=0, alpha=0.75,
        label="Variant B");

ax.set_xlabel('Purchase rate');
ax.set_yticklabels([]);
ax.legend();
In [28]:
fig
Out[28]:

The probability that variant B is better than variant A is

In [29]:
(ab_trace['a_rate'] < ab_trace['b_rate']).mean()
Out[29]:
0.7218

Robust Regression

In [30]:
x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5])
y = np.array([7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73])
In [31]:
fig, ax = plt.subplots(figsize=(8, 6))

ax.scatter(x, y, c='k', s=50);
In [32]:
fig
Out[32]:
In [33]:
X = np.empty((x.size, 2))
X[:, 0] = 1
X[:, 1] = x

coef, _, __, ___ = np.linalg.lstsq(X, y)
In [34]:
plot_X = np.ones((100, 2))

x_min, x_max = x.min() - 1, x.max() + 1
plot_X[:, 1] = np.linspace(x_min, x_max, 100)
In [35]:
fig, ax = plt.subplots(figsize=(8, 6))

ax.scatter(x, y, c='k', s=50);
ax.plot(plot_X[:, 1], plot_X.dot(coef),
        c='k', label='Least squares');

ax.set_xlim(x_min, x_max);
ax.legend(loc=2);
In [36]:
fig
Out[36]:
In [37]:
with pm.Model() as ols_model:
    # alpha is the slope and beta is the intercept
    alpha = pm.Uniform('alpha', -100, 100)
    beta = pm.Uniform('beta', -100, 100)
    
    # Ordinary least squares assumes that the noise is normally distributed
    y_obs = pm.Normal('y_obs', alpha + beta * x, 1., observed=y)

Applied interval-transform to alpha and added transformed alpha_interval to model.
Applied interval-transform to beta and added transformed beta_interval to model.
In [38]:
samples = 10000
In [39]:
with ols_model:
    step = pm.Metropolis()
    ols_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 10000 of 10000 complete in 2.2 sec
In [40]:
post_y = ols_trace['alpha'] + np.outer(plot_X[:, 1], ols_trace['beta'])
In [41]:
fig, ax = plt.subplots(figsize=(8, 6))

ax.fill_between(plot_X[:, 1],
                np.percentile(post_y, 2.5, axis=1),
                np.percentile(post_y, 97.5, axis=1),
                color='gray', alpha=0.5,
                label='95% CI');
ax.scatter(x, y, c='k', s=50);
ax.plot(plot_X[:, 1], plot_X.dot(coef),
        c='k', label='Least squares');
ax.plot(plot_X[:, 1], post_y.mean(axis=1),
        c='r', ls='--', label='PyMC3 least squares');

ax.set_xlim(x_min, x_max);
ax.legend(loc=2);
In [42]:
fig
Out[42]:
In [43]:
fig, ax = plt.subplots(figsize=(8, 6))

z = np.linspace(-4, 4, 100)

ax.plot(z, sp.stats.norm.pdf(z),
        label='$N(0, 1)$');
ax.plot(z, sp.stats.t.pdf(z, 3),
        label=r'$t(\nu = 3)$');

ax.set_xlabel('Residual');
ax.set_yticklabels([]);
ax.set_ylabel('Probability density');
ax.legend();
In [44]:
fig
Out[44]:
In [45]:
with pm.Model() as robust_model:
    # alpha is the slope and beta is the intercept
    alpha = pm.Uniform('alpha', -100, 100)
    beta = pm.Uniform('beta', -100, 100)
    
    # t-distributed residuals are less sensitive to outliers
    y_obs = pm.StudentT('y_obs', nu=3., mu=alpha + beta * x, observed=y)

Applied interval-transform to alpha and added transformed alpha_interval to model.
Applied interval-transform to beta and added transformed beta_interval to model.
In [46]:
with robust_model:
    step = pm.Metropolis()
    
    robust_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 10000 of 10000 complete in 2.3 sec
In [47]:
post_y_robust = robust_trace['alpha'] + np.outer(plot_X[:, 1], robust_trace['beta'])
In [48]:
fig, (l_ax, r_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(16, 6))

l_ax.fill_between(plot_X[:, 1],
                  np.percentile(post_y, 2.5, axis=1),
                  np.percentile(post_y, 97.5, axis=1),
                  color='gray', alpha=0.5,
                  label='95% CI');
l_ax.scatter(x, y, c='k', s=50);
l_ax.plot(plot_X[:, 1], plot_X.dot(coef),
          c='k', label='Least squares');
l_ax.plot(plot_X[:, 1], post_y.mean(axis=1),
          c='r', ls='--', label='PyMC3 least squares');

l_ax.set_xlim(x_min, x_max);
l_ax.legend(loc=2);

r_ax.fill_between(plot_X[:, 1],
                  np.percentile(post_y_robust, 2.5, axis=1),
                  np.percentile(post_y_robust, 97.5, axis=1),
                  color='gray', alpha=0.5,
                  label='95% CI');
r_ax.scatter(x, y, c='k', s=50);
r_ax.plot(plot_X[:, 1], post_y_robust.mean(axis=1),
          c=blue, label='PyMC3 robust');

r_ax.set_xlim(x_min, x_max);
r_ax.legend(loc=2);
In [49]:
fig
Out[49]:

Congressional Ideal Point Model

In [50]:
vote_data_uri = 'http://archive.ics.uci.edu/ml/machine-learning-databases/voting-records/house-votes-84.data'
In [51]:
N_BILLS = 16
BILLS = list(range(N_BILLS))

df = pd.read_csv(vote_data_uri, names=['party'] + BILLS)

df.index.name = 'rep'

df[df == 'n'] = 0
df[df == 'y'] = 1
df[df == '?'] = np.nan

df.party, parties = df.party.factorize()

N_REPS = df.shape[0]
In [52]:
df.head()
Out[52]:
party 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
rep
0 0 0 1 0 1 1 1 0 0 0 1 NaN 1 1 1 0 1
1 0 0 1 0 1 1 1 0 0 0 0 0 1 1 1 0 NaN
2 1 NaN 1 1 NaN 1 1 0 0 0 0 1 0 1 1 0 0
3 1 0 1 1 0 NaN 1 0 0 0 0 1 0 1 0 0 1
4 1 1 1 1 0 1 1 0 0 0 0 1 NaN 1 1 1 1
In [53]:
parties
Out[53]:
Index(['republican', 'democrat'], dtype='object')
In [54]:
vote_df = (pd.melt(df.reset_index(),
                   id_vars=['rep', 'party'], value_vars=BILLS,
                   var_name='bill', value_name='vote')
             .dropna()
             .astype(np.int64))
In [55]:
grid = sns.factorplot('bill', 'vote', 'party', vote_df,
                      kind='bar', ci=None, size=8, aspect=1.5);
grid.set_axis_labels('Bill', 'Percent voting for bill');
In [56]:
grid.fig
Out[56]:

$p_{i, j}$ is the probability that representative $i$ votes for bill $j$.

$$ \begin{align*} \log \left(\frac{p_{i, j}}{1 - p_{i, j}}\right) & = \gamma_j \left(\alpha_i - \beta_j\right) \\ & = \textrm{ability of bill } j \textrm{ to discriminate} \times (\textrm{conservativity of represetative } i\ - \textrm{conservativity of bill } j) \end{align*} $$
In [57]:
with pm.Model() as ideal_point_model:
    # The conservativity of representative i
    alpha = pm.Normal('alpha', 0, 1., shape=N_REPS)
    
    # The conservativity of bill j
    mu_beta = pm.Normal('mu_beta', 0, 1e-3)
    sigma_beta = pm.Uniform('sigma_beta', 0, 1e2)
    beta = pm.Normal('beta', mu_beta, sd=sigma_beta, shape=N_BILLS)
    
    # The ability of bill j to discriminate
    mu_gamma = pm.Normal('mu_gamma', 0, 1e-3)
    sigma_gamma = pm.Uniform('sigma_gamma', 0, 1e2)
    gamma = pm.Normal('gamma', mu_gamma, sd=sigma_gamma, shape=N_BILLS)
    
    # The probability that representative i votes for bill j
    p = pm.Deterministic('p', T.nnet.sigmoid(gamma[vote_df.bill] * (alpha[vote_df.rep] - beta[vote_df.bill])))
    
    # The observed votes
    vote = pm.Bernoulli('vote', p, observed=vote_df.vote)

Applied interval-transform to sigma_beta and added transformed sigma_beta_interval to model.
Applied interval-transform to sigma_gamma and added transformed sigma_gamma_interval to model.
In [58]:
samples = 20000
In [59]:
with ideal_point_model:
    step = pm.Metropolis()
    ideal_point_trace = pm.sample(samples, step, random_seed=SEED)

 [-----------------100%-----------------] 20000 of 20000 complete in 107.5 sec
In [60]:
rep_alpha = ideal_point_trace['alpha'].mean(axis=0)
In [61]:
fig, ax = plt.subplots(figsize=(8, 6))

ax.hist(rep_alpha[(df.party == (parties == 'republican').argmax()).values],
        normed=True, bins=10, color=red, alpha=0.75, lw=0,
        label='Republicans');
ax.hist(rep_alpha[(df.party == (parties == 'democrat').argmax()).values],
        normed=True, bins=10, color=blue, alpha=0.75, lw=0,
        label='Democrats');

ax.set_xlabel(r'$\alpha$');
ax.set_yticklabels([]);
ax.set_ylabel('Probability density');
ax.legend(loc=1);
In [62]:
fig
Out[62]:
In [63]:
pm.forestplot(ideal_point_trace, varnames=['gamma']);

Source: http://mqscores.berkeley.edu/

Probabilistic Programming Ecosystem

Probabilistic Programming System Language Discrete Variable Support Automatic Differentiation/Hamiltonian Monte Carlo Variational Inference
PyMC3 Python 2/3
PyMC2 Python 2/3
Stan C++, R, Python 2/3
BUGS Standalone program, R
JAGS Standalone program, R

References

PyMC3 examples repository (regression, matrix factorization, multilevel models, survival analysis, Gaussian process smoothing, Dirichlet processes), Bayesian neural nets)

Probabilistic Programming and Bayesian Methods for Hackers (Open source, uses PyMC2, PyMC3 port in progress)

Think Bayes (Available freely online, calculations in Python)

Bayesian Data Analysis

Thank You!

The Jupyter notebook these slides were generated from is available here