Luis Martí¶
Instituto de Computação¶
Universidade Federal Fluminense¶
$\newcommand{\vec}[1]{\boldsymbol{#1}}$
Why to study bio-inspired methods¶
- Nature is one of the best problem-solvers we know.
- Evolutionary optimization.
- Natural intelligence and artificial intelligence
- Cellular automata
- Neural computation
- Evolutionary computation
- Swarm intelligence
- Artificial immune systems
- Membrane computing
- Amorphous computing
Pigeons as art connoisseurs (Watanabe et al., 1995)¶
- Pigeons were put in a Skinner box, and
- presented with photos of paintings by Monet and Picasso.
- They were rewarded if they recognized correctly the painter they were presented with.



Results¶
- Pigeons were capable of discriminate between painters with an accuracy of 95% when confronted with paintings on the training set.
- Surprinsingly, they scored a 85% on paintings they had never seen during training (validation set).
- They were not just learning exhaustively which painting belonged to each painter.
- They were able to recognize styles or patterns and
- to generalize from what they had seen before.
In AI, we have been trying to replicate this capacity (and many others) in a computer for about 60 years.
Artificial neural networks¶
- Inspired (at different degrees) on the brain and the nervous system.
- Massive parallelization of relatively simple processing units.
- Simple principles lead to complex behaviours.
- Capable of learn form data.
Creating artificial neurons¶
Artificial neurons are designed to mimic aspects of their biological counterparts.
- **Dendrites** – act as the input receptor, allowing the cell to receive signals from a large (>1000) number of neighboring neurons. Each dendrite is able to perform a "multiplication" by that dendrite's "weight value."
- **Soma** – acts as a summation function. As positive and negative signals (exciting and inhibiting, respectively) arrive in the soma from the dendrites they are added together.
- **Axon** – gets its signal from the summation behavior which occurs inside the soma. The opening to the axon samples the electrical potential inside the soma. Once the soma reaches a certain potential, the axon will transmit an all-in signal pulse down its length.
- In this regard, the axon behaves as the ability for us to connect our artificial neuron to other artificial neurons.
The first artificial neuron was the Threshold Logic Unit (TLU), proposed by McCulloch and Pitts (1943).
The model was specifically targeted as a computational model of the "nerve net" in the brain.
As a transfer function, it employed a threshold, equivalent to using the Heaviside step function.
A simple model was considered, with binary inputs and outputs, and
restrictions on the possible weights, and a more flexible threshold value.
Any Boolean function could be implemented by networks of such devices, what is easily seen from the fact that one can implement the
ANDandORfunctions, and use them in the disjunctive or the conjunctive normal form.Cyclic TLU networks, with feedbacks through neurons, could define dynamical systems with memory, but
most research concentrated (and still does) on strictly feed-forward networks because of the smaller difficulty they pose.
Artificial neuron as a neuron abstraction¶
%tikz -s 700,200 -sc 1.0 -l shapes,calc,shapes,arrows -f svg \input{imgs/05/neuron.tikz}
pdf2svg terminated with signal -127 No image generated.
In general terms, an input $\vec{x}\in\mathbb{R}^n$ is multiplied by a weight vector $\vec{w}$ and added a bias $b$ producing the net activation, $\text{net}$. $\text{net}$ is passed to the activation function $f()$ that computed the neuron's output $\hat{y}$. $$ \hat{y} = f\left(\text{net}\right)= f\left(\vec{w}\cdot\vec{x}+b\right) = f\left(\sum_{i=1}^{n}{w_i x_i + b}\right). $$
The Perceptron¶
The Perceptron and its learning algorithm pioneered the research in neurocomputing.
- The perceptron is an algorithm for learning a linear binary classifier.
- That is a function that maps its input $\vec{x}\in\mathbb{R}^n$ (a real-valued vector) to an output value $f(\vec{x})$ (a single binary value) as,
where $\vec{w}$ is a vector of real-valued weights, $\vec{w} \cdot \vec{x}$ is the dot product $\sum_{i=1}^n w_i x_i$, and $b$ is known as the bias.
Perceptron learning¶
Learning goes by calculating the prediction of the perceptron, $\hat{y}$, as
$$\hat{y} = f\left(\vec{w}\cdot\vec{x} + b) = f( w_{1}x_{1} + w_2x_{2} + \cdots + w_nx_{n}+b\right)\,.$$After that, we update the weights and the bias using the perceptron rule:
$$ \begin{align*} w_i & = w_i + \alpha (y - \hat{y}) x_{i} \,,\ i=1,\ldots,n\,;\\ b & = b + \alpha (y - \hat{y})\,. \end{align*} $$Here $\alpha\in\left(0,1\right]$ is known as the learning rate.
Mark I: The Perceptron implementation¶

- An array of cadmium sulfide photocells was used for capturing 20x20 (400) pixel images that were used as inputs.
- A switchboard was used for manually selecting which input elements (pixels) were passed to the perceptrons.
- They used potentiometers as variable weights.
- Electric motors automatically modified the weights.
Implementing the Perceptron¶
We are going to start implementing a perceptron as a class.
class Perceptron:
'A simple Perceptron implementation.'
def __init__(self, weights, bias, alpha=0.1):
self.weights = weights
self.bias = bias
self.alpha = alpha
def propagate(self, x):
return self.activation(self.net(x))
def activation(self, net):
if net > 0:
return 1
return 0
def net(self, x):
return np.dot(self.weights, x) + self.bias
def learn(self, x, y):
y_hat = self.propagate(x)
self.weights = [ w_i + self.alpha*x_i*(y-y_hat) for (w_i, x_i) in zip(self.weights, x)]
self.bias = self.bias + self.alpha*(y-y_hat)
return np.abs(y_hat - y)
Testing our Perceptron class.¶
After having the perceptron implementation ready we need an example data set.
We are going to create a dataset containing random points in $\left[0,1\right]^2$.
size = 50 # size of data set
data = pd.DataFrame(columns=('$x_1$', '$x_2$'),
data=np.random.uniform(size=(size,2)))
So far, our data set looks like this (we are showning only the first ten elements):
data.head(10)
| $x_1$ | $x_2$ | |
|---|---|---|
| 0 | 0.939672 | 0.304112 |
| 1 | 0.748428 | 0.754524 |
| 2 | 0.990574 | 0.641591 |
| 3 | 0.426878 | 0.825523 |
| 4 | 0.786634 | 0.900275 |
| 5 | 0.625920 | 0.180962 |
| 6 | 0.568821 | 0.271016 |
| 7 | 0.990957 | 0.878344 |
| 8 | 0.223451 | 0.383407 |
| 9 | 0.570892 | 0.631924 |
We need to add a target or classification attribute. In this example, we are going to make this target to be equal to one if the point lies in the upper-right triangle of the $\left[0,1\right]\times\left[0,1\right]$ square and zero otherwise:
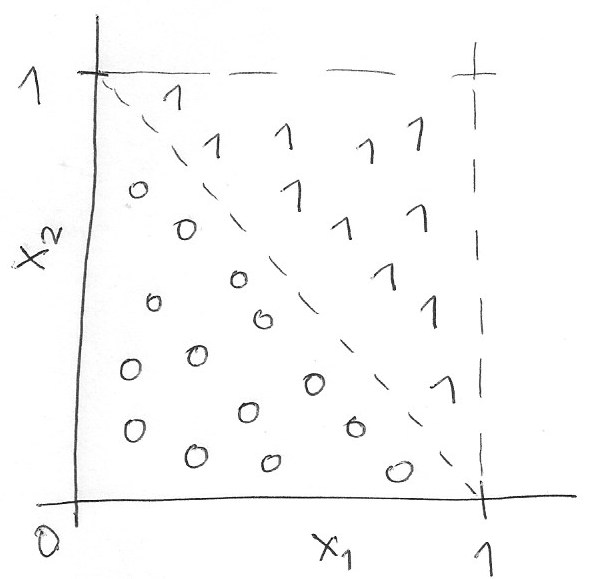
We can formalize this condition as:
$$ y = \begin{cases} 1 & \ \text{if}\ x_1 + x_2 > 1\,,\\ 0 & \ \text{otherwise}\,. \end{cases} $$Lets code it...
def condition(x):
return int(np.sum(x) > 1)
...and apply it to the data set.
data['y'] = data.apply(condition, axis=1)
The resulting data set looks like this:
data.head(10)
| $x_1$ | $x_2$ | y | |
|---|---|---|---|
| 0 | 0.939672 | 0.304112 | 1 |
| 1 | 0.748428 | 0.754524 | 1 |
| 2 | 0.990574 | 0.641591 | 1 |
| 3 | 0.426878 | 0.825523 | 1 |
| 4 | 0.786634 | 0.900275 | 1 |
| 5 | 0.625920 | 0.180962 | 0 |
| 6 | 0.568821 | 0.271016 | 0 |
| 7 | 0.990957 | 0.878344 | 1 |
| 8 | 0.223451 | 0.383407 | 0 |
| 9 | 0.570892 | 0.631924 | 1 |
We can now take a better look at the data set in graphical form. Elements with $y=1$ are shown in green ($\color{green}{\bullet}$) and those with $y=0$ are shown in red ($\color{red}{\bullet}$):
def plot_data(data, ax):
data[data.y==1].plot(kind='scatter',
x='$x_1$', y='$x_2$',
color='green', ax=ax)
data[data.y==0].plot(kind='scatter',
x='$x_1$', y='$x_2$',
color='red', ax=ax)
ax.set_xlim(-0.1,1.1); ax.set_ylim(-0.1,1.1)
fig = plt.figure(figsize=(5,5))
plot_data(data, fig.gca())
Iterating the data set¶
Having the data set we can now code how the perceptron learns it by iterating throu it.
def learn_data(perceptron, data):
'Returns the number of errors made.'
count = 0
for i, row in data.iterrows():
count += perceptron.learn(row[0:2], row[2])
return count
Visualizing learning¶
We need now to plot the decision boundary or threshold of the perceptron.
To calculate it we start with the equation that describes the boundary, $$w_1x_1+w_2x_2 + b =0.$$
From it we can obtain $x_2$ from a given $x_1$ applying a fairy simple math, $$x_2 = \frac{-w_1x_1-b}{w_2}.$$
def threshold(perceptron, x_1):
return (-perceptron.weights[0] * x_1 - perceptron.bias) / perceptron.weights[1]
Our perceptron in action¶
All set now! Let's create a perceptron and train it.
Note: Normally the initial weights and the bias should be set to small random values. I am setting them by hand to a value that I know that looks good in the examples.
perceptron = Perceptron([0.1,-0.1], 0.02)
f, axarr = plt.subplots(3, 4, sharex=True, sharey=True, figsize=(9,7))
axs = list(itertools.chain.from_iterable(axarr))
for t in range(12):
plot_all(perceptron, data, t, ax=axs[t])
learn_data(perceptron, data)
f.tight_layout()
It is clear how the Perceptron threshold is progresively adjusted according to the data set.
Animating the Perceptron¶
This results are better understood in animated from.
fig = plt.figure(figsize=(4,4))
ax = fig.gca()
perceptron = Perceptron([0.1,-0.1], 0.02)
anim = animation.FuncAnimation(fig, lambda i: animate(i, perceptron, data, ax), frames=30, interval=600,
blit=False)
plt.tight_layout()
plt.close()
HTML(anim.to_html5_video())
Self-study¶
- Experiment with the learning rate ($\alpha$). How it impacts learning? Do you remember if we have seen another similar parameter in previous classes?
- Create a new data set with a non-linear boundary. What happens now with our perceptron? How would you fix it?
Suggested reading¶
- Minsky M. L. and Papert S. A. (1969). Perceptrons. Cambridge, MA: MIT Press.
- Gallant, S. I. (1990). Perceptron-based learning algorithms. IEEE Transactions on Neural Networks, vol. 1, no. 2, pp. 179–191.
- Mikel Olazaran (1996). A Sociological Study of the Official History of the Perceptrons Controversy. Social Studies of Science 26 (3): 611–659. doi:10.1177/030631296026003005.
The XOR issue¶
Take a dataset that contains all the possible value combination of the logical XOR function:
X = np.array([[0, 1], [1, 0], [0, 0], [1, 1]])
Y = np.array([1, 1, 0, 0])
N = Y.shape[0]
The data set has ones (represented in black) when $x_1 = 1$ and $x_2 = 0$ or when $x_1 = 0$ and $x_2 = 1$, as defined for the XOR function.
plt.scatter(X[:, 0], X[:, 1], c=Y, edgecolor='k', cmap=cm.gray_r, s=100)
plt.xlabel('$x_1$');plt.ylabel('$x_2$');
It is evident that a perceptron is unable to solve this simple problem as it is only able to separate the space by a hyperplane.
To solve the XOR problem we need to stack perceptrons
%tikz -s 500,250 -sc 1.0 -l positioning -f svg \input{imgs/05/xor-nn.tikz}
pdf2svg terminated with signal -127 No image generated.
But, how can we train the weights from neurons 1 and 2?
- This is known as a credit assignment problem.
- Our current method for Perceptron learning determine how the weights of neurons 1 and 2 influence the error.
- Let's visualize it.
A "handcoded" XOR neural network¶
Forward propagation for 2 inputs $(x_1, x_2)$, 2 hidden nodes, 1 output.
- We will be extending the Perceptron activation as the logistic (logit) function
def logit(a):
return 1.0 / (1+np.exp(-a))
def fprop(x1, x2,
w1= 0.1, w2= 0.2, b1= 0.1,
w3=-0.2, w4= 0.2, b2=-0.1,
w5=-0.3, w6=-0.25, b3=0.2):
y_hat_1 = logit(b2 + w3*x1 + w4*x2) # N1
y_hat_2 = logit(b3 + w5*x1 + w6*x2) # N2
return logit(b1 + w1*y_hat_1 + w2*y_hat_2)
Error Surface of the XOR Problem¶
@interact(i=(1,6), j=(1,6))
def error_plot(i=5, j=6):
W1, W2 = np.meshgrid(np.arange(-10, 10, 0.5), np.arange(-10, 10, 0.5))
E = np.sum([(fprop(X[n, 0], X[n, 1],
**{"w%d"%(i) : W1, "w%d"%(j) : W2})-Y[n])**2
for n in range(N)], axis=0)
ax = plt.figure(figsize=(7, 4.5)).add_subplot(111, projection="3d")
surf = ax.plot_surface(W1, W2, E, rstride=1, cstride=1, cmap=cm.viridis, lw=0.11, alpha=0.74)
plt.setp(ax, xlabel="$w_%d$" % (i), ylabel="$w_%d$" % (j), zlabel="$E()$");
plt.tight_layout()
plt.show()
Failed to display Jupyter Widget of type interactive.
If you're reading this message in the Jupyter Notebook or JupyterLab Notebook, it may mean that the widgets JavaScript is still loading. If this message persists, it likely means that the widgets JavaScript library is either not installed or not enabled. See the Jupyter Widgets Documentation for setup instructions.
If you're reading this message in another frontend (for example, a static rendering on GitHub or NBViewer), it may mean that your frontend doesn't currently support widgets.
Local Minima¶
@interact(i=(0,5), j=(0,5))
def errors_plot(i=0, j=1):
plt.figure(figsize=(12, 3))
W = np.arange(-10, 10, 0.25)
errors = [(fprop(X[n, 0], X[n, 1], **{"w%d"%(i+1) : W, "w%d"%(j+1) : W+2})-Y[n])**2 for n in range(N)]
plt.subplot(1, 2, 1)
for n in range(N):
plt.plot(W, errors[n], label="$E^{(%d)}$" % (n+1))
plt.setp(plt.gca(), xlabel="$w$", ylabel="$E$", title='Split errors');plt.legend(loc="best", frameon=True)
plt.subplot(1, 2, 2)
plt.plot(W, np.sum(errors, axis=0), label="$E(\cdot)$")
plt.setp(plt.gca(), xlabel="$w$", ylabel="$E$", title='Total error');plt.legend(loc="best", frameon=True);
plt.show()
Failed to display Jupyter Widget of type interactive.
If you're reading this message in the Jupyter Notebook or JupyterLab Notebook, it may mean that the widgets JavaScript is still loading. If this message persists, it likely means that the widgets JavaScript library is either not installed or not enabled. See the Jupyter Widgets Documentation for setup instructions.
If you're reading this message in another frontend (for example, a static rendering on GitHub or NBViewer), it may mean that your frontend doesn't currently support widgets.
The Multilayer Perceptron (MLP)¶
The composition of layers of perceptrons can capture complex relations between inputs and outputs in a hierarchical way.
%tikz -s 600,400 -sc 1.0 -l positioning -f svg \input{imgs/05/neural-network.tikz}
pdf2svg terminated with signal -127 No image generated.
...but how can we adapt the weights of the neurons in the hidden layers?
Improving the notation¶
In order to proceed we need to improve the notation we have been using. That for, for each layer $1\geq l\geq L$, the activations and outputs are calculated as:
$$\text{net}^l_j = \sum_i w^l_{ji} x^l_i\,,$$$$y^l_j = f^l(\text{net}^l_j)\,,$$where:
- $y^l_j$ is the $j$th output of layer $l$,
- $x^l_i$ is the $i$th input to layer $l$,
- $w^l_{ji}$ is the weight of the $j$-th neuron connected to input $i$,
- $\text{net}^l_{j}$ is called net activation, and
- $f^l(\cdot)$ is the activation function of layer $l$, e.g. $\tanh()$, in the hidden layers and the identity in the last layer (for regression)
Error function (SSE)¶
- For $\Psi=\left\{\left<\vec{x}^{(1)},\vec{y}^{(1)}\right>,\ldots,\left<\vec{x}^{(k)},\vec{y}^{(k)}\right>,\ldots\left<\vec{x}^{(K)},\vec{y}^{(K)}\right>\right\}$:
Training MLPs with Backpropagation¶
- Backpropagation of errors is a procedure to compute the gradient of the error function with respect to the weights of a neural network.
- We can use the gradient from backpropagation to apply gradient descent!
A math flashback¶
The chain rule can be applied in composite functions as, $$ \left( f \circ g\right)'(x) = \left(f\left(g\left(x\right)\right)\right)'= f'\left(g(x)\right)g'(x). $$ or, in Leibniz notation, $$ \frac{\partial f\left(g\left(x\right)\right)}{\partial x} = \frac{\partial f\left(g\left(x\right)\right)}{\partial g\left(x\right)} \cdot \frac{\partial g\left(x\right)}{\partial x} $$
The total derivative of $f(x_1,x_2,...x_n)$ on $x_i$ is $$ \frac{\partial f}{\partial x_i}= \sum_{j=1}^n{\frac{\partial f}{\partial x_j}\cdot\frac{\partial x_j}{\partial x_i}} $$
To apply gradient descent we need... to calculate the gradients¶
Applying the chain rule, $$ \frac{\partial \ell}{\partial w^l_{ji}}= \color{blue}{\overbrace{\frac{\partial \ell}{\partial \text{net}^l_j}}^{\delta^l_j}} \color{forestgreen}{\underbrace{\frac{\partial{\text{net}^l_j}}{\partial w^l_{ji}}}_{\frac{\partial\left(\sum_{i}w^l_{ji}x^l_i\right)}{\partial w^l_{ji}}=x^l_i}} $$ hence we can write $$ \frac{\partial \ell}{\partial w^l_{ji}}= \color{blue}{\delta^l_j} \color{forestgreen}{x^l_i} $$
For the output layer ($l=L$)¶
$$ \delta^L_j = \frac{\partial \ell}{\partial \text{net}^L_j} = \color{red}{ \overbrace{ \frac{\partial \ell}{\partial\hat{y}^L_j}}^{\frac{\partial\left(\frac{1}{2}\sum_j{\left(y_j-\hat{y}^L_j\right)^2} \right)} {\partial\hat{y}^L_j}=\left(y_j-\hat{y}^L_j\right)}} \cdot \color{magenta}{ \underbrace{\frac{\partial\hat{y}^L_j}{\text{net}^l_j}}_{f'(\text{net}_j^L)}} =\color{red}{\left(y_j-\hat{y}^L_j\right)}\color{magenta}{f'(\text{net}_j^L)}. $$therefore $$ \frac{\partial \ell}{\partial w^L_{ji}}= \color{red}{\left(y_j-\hat{y}^L_j\right)}\color{magenta}{f'(\text{net}_j^L)} \color{forestgreen}{x^L_i} $$
What about the hidden layers ($1\leq l<L$)?¶
We can express the loss $\ell$ as a function of the activations of the subsequent layer,
$$ \ell = \ell\left(\text{net}^{l+1}_1,\ldots,\text{net}^{l+1}_K\right)\,, $$therefore, applying total derivatives,
$$ \frac{\partial \ell}{\partial\hat{y}^l_j} = \frac{\partial \ell\left(\text{net}^{l+1}_1,\ldots,\text{net}^{l+1}_K\right)}{\partial\hat{y}^l_j}\,. $$Applying total derivatives we get¶
$$ \frac{\partial \ell}{\partial\hat{y}^l_j} = \sum_{k}{ \color{orange}{ \overbrace{ \frac{\partial \ell}{\partial\text{net}^{l+1}_k}}^{\delta^{l+1}_k}} \color{purple}{ \underbrace{\frac{\partial \text{net}^{l+1}_{k}}{\partial\hat{y}^l_j} }_{\frac{\partial{\sum_{j}{w^{l+1}_{kj}\hat{y}^l_j}}}{\partial\hat{y}^l_j}=w^{l+1}_{kj}}} } = \sum_{k}{\color{orange}{\delta^{l+1}_k}\color{purple}{w^{l+1}_{kj}}} $$Back-propagating the errors to the hidden layer¶
The $\delta$s of the subsequent layers are used to calculate the $\delta$s of the more internal ones.
$$ \delta^{l}_j = \frac{\partial\ell}{\partial\text{net}^l_j} = \overbrace{\frac{\partial\ell}{\partial\hat{y}^l_j}}^ {\sum_{k}{ \color{orange}{\delta^{l+1}_k} \color{purple}{w^{l+1}_{kj}}}} \color{forestgreen}{\underbrace{\frac{\partial\hat{y}^l_j}{\partial\text{net}^l_j}}_ {f'(\text{net}^l_j)}}= \sum_{k}{\left( \color{orange}{\delta^{l+1}_k} \color{purple}{w^{l+1}_{kj}} \right)}\color{forestgreen}{f'(\text{net}^l_j)} $$Backpropagation in brief¶
In each layer (we will omit the sample index $k$ and layer $l$)
$$ \delta_j = \begin{cases} \hat{y}_j - y_j & \text{in the output layer,}\\ \\ f'(\text{net}_j) \sum_k \frac{\partial \ell}{\partial \hat{y}_k} & \text{otherwise.} \end{cases} $$$$\frac{\partial \ell}{\partial w_{ji}} = \delta_j x_i\,;\quad \frac{\partial \ell}{\partial x_i} = \delta_j w_{ji}\,.$$where
- all nodes $k$ are in the layer after $j$;
- $\text{net}_j$ is known from propagation: $\sum_i w_{ji} x_i$;
- actually you do not have to save $a_j$ because $g'(a_j)$ usually can be computed from $y_j$, e.g.
- identity function: $f'(\text{net}_j) = 1$,
- $\tanh$: $f'(\text{net}_j) = 1 - y_j^2$;
- $\frac{\partial \ell}{\partial w_{ji}}$ will be used to update the weight $w_{ji}$ in gradient descent;
- $\frac{\partial \ell}{\partial x_i}$ will be passed to the previous layer to compute the deltas;
Do not forget to sum up the gradient with respect to the weights for each training example!
Efficient Implementation for Fully Connected Layers¶
- Make sure that you have an efficient linear algebra library.
- Organize your data in matrices, i.e.
- The matrix $\boldsymbol{X}$ contains an input vector in each row. Note that you must expand each row by the bias 1.
- The matrix $\boldsymbol{T}$ contains an output (of the network) in each row.
- Each layer should have the functions
fprop(W, X, f) -> Ybackprop(W, X, f_derivative, Y, d_loss/dY) -> d_loss/dX, d_lossdW
Efficient forward propagation¶
In each layer
$$\boldsymbol{NET} = \boldsymbol{X} \boldsymbol{W}^\intercal$$$$\boldsymbol{\hat{Y}} = f(\boldsymbol{NET})$$where
- $\boldsymbol{Y} \in \mathbb{R}^{N \times J}$ contains an output vector in each row, i.e. $\boldsymbol{Y}_{kj} = y^{(k)}_j$
- $\boldsymbol{X} \in \mathbb{R}^{N \times I}$ contains an input vector (the output of the previous layer) in each row, i.e. $\boldsymbol{X}_{ki} = x^{(k)}_i$
- $\boldsymbol{W} \in \mathbb{R}^{J \times I}$ is the weight matrix of the layer, i.e. $\boldsymbol{W}_{ji}$ is the weight between input $i$ and output $j$.
- $f$ is the activation function (implemented to work with matrices)
- $I$ is the number of inputs, i.e. the number of outputs of the previous layer plus 1 (for the bias)
- $J$ is the number of outputs
Make sure that you add the bias entry in each row before you pass $Y$ as input to the next layer!
Error function (SSE)
$$E = \frac{1}{2} ||\boldsymbol{Y} - \boldsymbol{T}||_2^2$$where
- $||\cdot||_2$ is the Frobenius norm.
Efficient Backpropagation¶
In each layer:
$$\Delta = f'(\boldsymbol{NET}) \ast \frac{\partial \ell}{\partial \boldsymbol{Y}}\,,$$$$\frac{\partial \ell}{\partial \boldsymbol{W}} = \Delta^T \cdot \boldsymbol{X}\,,$$$$\frac{\partial \ell}{\partial \boldsymbol{X}} = \Delta \cdot \boldsymbol{W}\,.$$where:
- $*$ is the Hadamard product or Schur product or entrywise product
- $\frac{\partial \ell}{\partial \boldsymbol{Y}}$ contains derivatives of the error function with respect to the outputs ($\boldsymbol{Y} - \boldsymbol{T} = \frac{\partial \ell}{\partial \boldsymbol{Y}}$ in the last layer)
- $\frac{\partial \ell}{\partial \boldsymbol{X}} \in \mathbb{R}^{N \times I}$ contains derivatives of the error function with respect to the inputs and will be passed to the previous layer
- $\Delta \in \mathbb{R}^{N \times J}$ contains deltas: $\delta_j^{(n)} = \Delta_{jn}$
- $g'$ is the derivative of $g$ and can be computed based only on $\boldsymbol{Y}$
- $\frac{\partial \ell}{\partial \boldsymbol{W}} \in \mathbb{R}^{J \times I}$ contains the derivatives of the error function with respect to $\boldsymbol{W}$ and will be used to optimize the weights of the ANN
Make sure that you remove the bias entry in each row before you pass $\frac{\partial \ell}{\partial \boldsymbol{X}}$ to the previous layer!
Pseudocode of backpropagation¶
pseudo
initialize network weights (often small random values)
do
foreach training example, x
prediction = neural-net-output(network, x) // forward pass
actual = teacher-output(x)
compute error (prediction - actual) at the output units
compute deltas for all weights from hidden layer to output layer // backward pass
compute deltas for all weights from input layer to hidden layer // backward pass continued
update network weights // input layer not modified by error estimate
until all examples classified correctly or another stopping criterion satisfied
return the network
Tips for Your Implementations¶
- Depending on the problem type you have to select different activation functions for the output layer.
- Check your gradients with finite differences:
How to initialize weights $\boldsymbol{w}$?¶
np.random.randn(10) * 0.05
array([-0.05466522, 0.04519595, -0.12944682, -0.05341159, -0.00769046,
-0.04324446, -0.07862767, 0.01952648, 0.04378596, 0.06973566])
- Draw components of $\boldsymbol{w}$ iid (independend and identically distributed) from a Gaussian distrubition with small standard deviation, e.g. 0.05.
- Initialization with 0 will prevent the gradient from flowing back to the lower layers as
- It has been shown that initialization of weights is a key to have good results. See:
- Glorot, X., & Bengio, Y. (2010).Understanding the difficulty of training deep feedforward neural networks. Proceedings of the 13th International Conference on Artificial Intelligence and Statistics (AISTATS), 9, 249–256. http://doi.org/10.1.1.207.2059
def plot_afun(x, y, sp_idx, label=None):
"""Plot activation function."""
ax = plt.subplot(2, 4, sp_idx)
if label is not None:
plt.title(label)
plt.setp(ax, xlim=(np.min(x), np.max(x)), ylim=(np.min(y)-0.5, np.max(y)+0.5))
plt.plot(x, y)
plt.figure(figsize=(10, 4))
x = np.linspace(-5, 5, 100)
plot_afun(x, x, 1, label="Identity")
plot_afun(x, np.tanh(x), 2, label="tanh")
plot_afun(x, logit(x), 3, label="Logistic (logit)")
plot_afun(x, np.max((x, np.zeros_like(x)), axis=0), 4, label="Rectified \nLinear Unit (ReLU)")
plot_afun(x, np.ones_like(x), 5)
plot_afun(x, 1-np.tanh(x)**2, 6)
plot_afun(x, logit(x)*(1-logit(x)), 7)
plot_afun(x, np.max((np.sign(x), np.zeros_like(x)), axis=0), 8)
Derivatives of Activation Functions¶
- Identity
- Hyperbolic tangent
- Logistic function
Summarizing¶
- We now know how to compute the $\frac{\partial\ell}{\partial w^l_{ji}}$ for all neurons.
- For the neurons on the hidden layers we use the $\delta$s of the next layer.
- We know how to updates the weights as:
Difficulties¶
- There are many local minima.
- The optimization problem is ill-conditioned.
- There are many flat regions (saddle points).
- There is no guarantee to reach the global minimum.
- Deep architectures suffer from the vanishing gradient problem.
- Neural networks are usually considered to be the blackest box of all learning algorithms.
- There are sooo many hyperparameters (number of layers/nodes, activation function, connectivity, weight initialization, loss function, regularization, ...).
- Training neural networks has been regarded as black magic by many researchers.
- And here is the grimoire: Neural Networks: Tricks of the Trade (1st edition: 1998; 2nd edition: 2012).
Theoretical features¶
Universal approximation theorem:
A feed-forward network with a single hidden layer containing a finite number of neurons can approximate any continuous functions on compact subsets of $\mathbb{R}^n$, under mild assumptions on the activation function.
Hornik showed in 1991 that it is not the specific choice of the activation function, but rather the multilayer feedforward architecture itself which gives neural networks the potential of being universal approximators.
Kurt Hornik (1991) Approximation Capabilities of Multilayer Feedforward Networks, Neural Networks, 4(2), 251–257
There have been three hypes around ANNs:
- Perceptron (50s-XOR problem)
- Backpropagation (80s-SVM)
- Deep Learning (2006-now)
And they work incredibly well in practice.
But... why do neural nets work well in practice?¶
- Universal function approximation property.
- Stochastic gradient descent finds sufficiently good local minima.
- We don't want to find the global minimum $\implies$ ** fights overfitting!**
- Neural nets learn feature hierarchies to represent functions efficiently.
- features will be learned automatically
- allows learning of hierarchical features which is much more efficient than just one layer of abstraction
- multiclass classification can be integrated with linear complexity (softmax activation function, cross-entropy error function)
- it is a parametric model, it does not store any training data directly.
Drawbacks¶
- input has to be a vector of real numbers, e.g. text must be converted before classification
- in general, the optimization problem is very difficult because it is ill-conditioned and non-separable
- objective function is not convex, there are many local minima and flat regions
- black box: in most cases it is very difficult to interpret the weights of a neural network although it is possible!
- catastrophic forgetting: learning one instance can change the whole network

