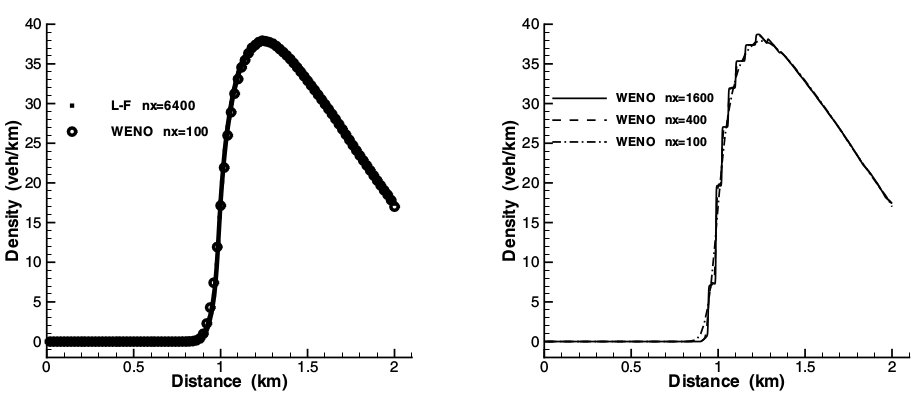
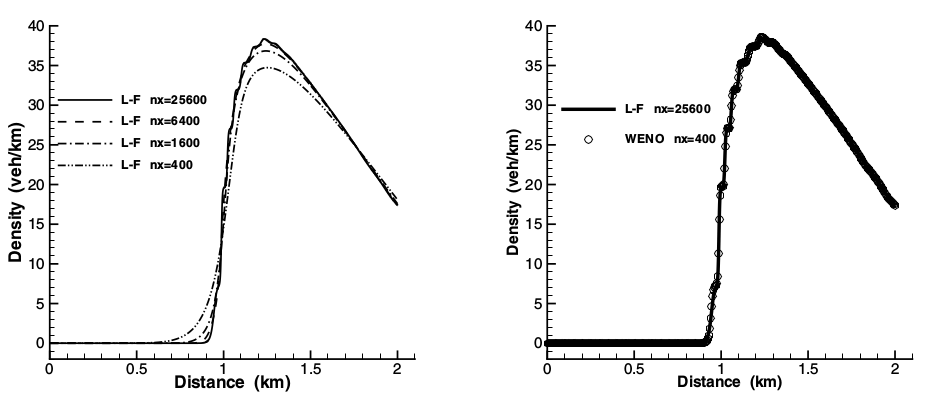
Finite Volume
WENO interpolation ... [is] used ... to transfer information from one domain to another in a high order, nonoscillatory fashion

Finite Difference
Define $h(x)$ implicitly via $$\frac{1}{\Delta x} \int_{x - \Delta x / 2}^{x + \Delta x / 2} h(s) \, ds = f(u(x))$$
weno_computations.make_intro_plots(0)
weno_computations.make_intro_plots(1)
weno_computations.make_intro_plots(2)
weno_computations.make_intro_plots(3)
weno_computations.make_intro_plots(4)
weno_computations.make_intro_plots(5)
weno_computations.make_intro_plots(6)
weno_computations.make_intro_plots(7)
weno_computations.make_intro_plots(8)
weno_computations.make_intro_plots(9)
weno_computations.make_intro_plots(10)
weno_computations.make_intro_plots(11)
weno_computations.make_intro_plots(12)
Putting the W in WENO: $$u^{{(\ast)}}_{{j + \frac{1}{2}}} = \frac{1}{10} u^{{(1)}}_{{j + \frac{1}{2}}} + \frac{6}{10} u^{{(2)}}_{{j + \frac{1}{2}}} + \frac{3}{10} u^{{(3)}}_{{j + \frac{1}{2}}}$$
What about the other letters?
What about shocks?
weno_computations.discontinuity_to_volume_single_cell(0)
weno_computations.discontinuity_to_volume_single_cell(1)
weno_computations.make_shock_plot_single_cell()
weno_computations.discontinuity_to_volume()
weno_computations.make_shock_plot()
Smoothness indicator when approximating a point in the interval $I = \left(x_j - \frac{\Delta x}{2}, x_j + \frac{\Delta x}{2}\right]$
Large $\beta$ indicates that the approximation $p(x)$ is not smooth nearby our point.
Recall the W in WENO: $$u^{{(\ast)}}_{{j + \frac{1}{2}}} = \frac{1}{10} u^{{(1)}}_{{j + \frac{1}{2}}} + \frac{6}{10} u^{{(2)}}_{{j + \frac{1}{2}}} + \frac{3}{10} u^{{(3)}}_{{j + \frac{1}{2}}}$$
Rather than using these directly, incorporate a penalty for each polynomial approximation's (lack of) smoothness: $\beta^{(1)}$, $\beta^{(2)}$, $\beta^{(3)}$.
Back to Conservation Law
TV-diminishing / strong stability preserving RK scheme
$$\begin{array}{c | c c c} 0 & & & \\ 1 & 1 & & \\ 1/2 & 1/4 & 1/4 & \\ \hline & 1/6 & 1/6 & 2/3 \end{array}$$
Example