Introduction to Probabilistic Programming¶
DataPhilly¶
July 13, 2016¶
@Austin Rochford (arochford@monetate.com)¶
Probabilistic Programming¶
- Programming with random variables
- User specifies a generative model for the observed data
- "Tell the story" of how the data were created
- The language runtime/software library automatically performs inference

What do we mean by inference?¶
- Maximum likelihood inference
- Maxumum a posteriori inference
- Full posterior inference
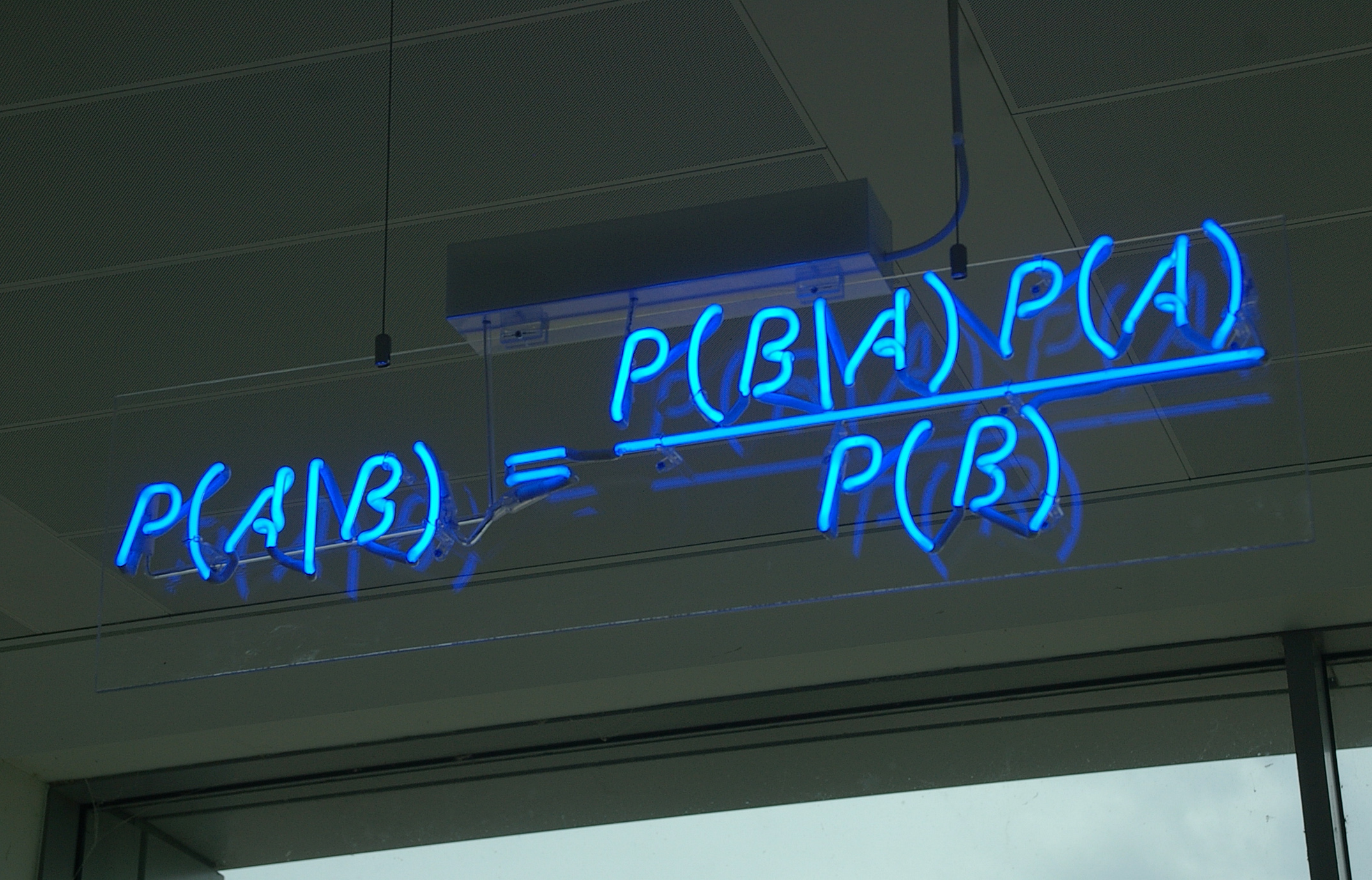
Disease Testing¶
A certain rare disease affects one in 10,000 people. A test for the disease gives the correct result 99.9% of the time.
What is the probability that a given test is positive?
import pymc3 as pm
with pm.Model() as pretest_disease_model:
# This is our prior belief about whether or not the subject has the disease,
# given its prevalence of the disease in the general population
has_disease = pm.Bernoulli('has_disease', 1e-4)
# This is the probability of a positive test given the presence or lack
# of the disease
p_positive = pm.Deterministic('p_positive',
T.switch(T.eq(has_disease, 1),
# If the subject has the disease,
# this is the probability that the
# test is positive
0.999,
# If the subject does not have the
# disease, this is the probability
# that the test is negative
1 - 0.999))
# This is the observed test result
test_positive = pm.Bernoulli('test_positive', p_positive)
samples = 40000
with pretest_disease_model:
step = pm.Metropolis()
pretest_disease_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 40000 of 40000 complete in 6.1 sec
pretest_disease_trace['test_positive']
array([0, 0, 0, ..., 0, 0, 0])
pretest_disease_trace['test_positive'].size
40000
The probability that a given test is positive is
pretest_disease_trace['test_positive'].mean()
0.001575
0.999 * 1e-4 + (1 - 0.999) * (1 - 1e-4)
0.0010998000000000008
If a subject tests positive, what is the probability they have the disease?
with pm.Model() as disease_model:
# This is our prior belief about whether or not the subject has the disease,
# given its prevalence of the disease in the general population
has_disease = pm.Bernoulli('has_disease', 1e-4)
# This is the probability of a positive test given the presence or lack
# of the disease
p_positive = pm.Deterministic('p_positive',
T.switch(T.eq(has_disease, 1),
# If the subject has the disease,
# this is the probability that the
# test is positive
0.999,
# If the subject does not have the
# disease, this is the probability
# that the test is negative
1 - 0.999))
# This is the observed positive test
test_positive = pm.Bernoulli('test_positive', p_positive, observed=1)
with disease_model:
step = pm.Metropolis()
disease_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 40000 of 40000 complete in 3.8 sec
The probability that someone who tests positive for the disease has it is
disease_trace['has_disease'].mean()
0.096775
0.999 * 1e-4 / (0.999 * 1e-4 + (1 - 0.999) * (1 - 1e-4))
0.09083469721767587
The Monty Hall Problem¶

If we select the first door and Monty opens the third to reveal a goat, should we change doors?
with pm.Model() as monty_model:
# We have no idea where the prize is at the beginning
prize = pm.DiscreteUniform('prize', 0, 2)
# The probability that Monty opens each door
p_open = pm.Deterministic('p_open',
T.switch(T.eq(prize, 0),
# If the prize is behind the first door,
# he chooses to open one of the others
# at random
np.array([0., 0.5, 0.5]),
T.switch(T.eq(prize, 1),
# If it is behind the second door,
# he must open the third door
np.array([0., 0., 1.]),
# If it is behind the third door,
# he must open the second door
np.array([0., 1., 0.]))))
# Monty opened the third door, revealing a goat
opened = pm.Categorical('opened', p_open, observed=2)
samples = 10000
with monty_model:
step = pm.Metropolis()
monty_trace = pm.sample(samples, step, random_seed=SEED)
monty_trace_df = pm.trace_to_dataframe(monty_trace)
[-----------------100%-----------------] 10000 of 10000 complete in 1.4 sec
monty_trace_df.head()
| p_open__0 | p_open__1 | p_open__2 | prize | |
|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 1.0 | 1 |
| 1 | 0.0 | 0.5 | 0.5 | 0 |
| 2 | 0.0 | 0.0 | 1.0 | 1 |
| 3 | 0.0 | 0.0 | 1.0 | 1 |
| 4 | 0.0 | 0.0 | 1.0 | 1 |
(monty_trace_df.groupby('prize')
.size()
.div(monty_trace_df.shape[0]))
prize 0 0.3196 1 0.6804 dtype: float64
Built on top of theano
- Dynamic generation of
Ccode for models - Automatic differentiation allows for gradient-based inference
- Implements advanced Markov chain Monte carlo algorithms, such at the No U-Turn Sampler
- Implements automatic differentiation variational inference
- Interoperable with both
pandasandpatsy - Provides clean support for multilevel models

A/B Testing¶

Suppose variant A sees 510 visitors and 40 purchases, but variant B sees 505 visitors and 50 conversions.
with pm.Model() as ab_model:
# A priori, we have no idea what the purchase rate for variant A will be
a_rate = pm.Uniform('a_rate')
# We observed 40 purchases from 510 visitors who saw variant A
a_purchases = pm.Binomial('a_purchases', 510, a_rate, observed=40)
# A priori, we have no idea what the purchase rate for variant B will be
b_rate = pm.Uniform('b_rate')
# We observed 40 purchases from 510 visitors who saw variant A
b_purchases = pm.Binomial('b_purchases', 505, b_rate, observed=45)
Applied interval-transform to a_rate and added transformed a_rate_interval to model. Applied interval-transform to b_rate and added transformed b_rate_interval to model.
samples = 10000
with ab_model:
step = pm.NUTS()
ab_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 10000 of 10000 complete in 3.2 sec
fig
The probability that variant B is better than variant A is
(ab_trace['a_rate'] < ab_trace['b_rate']).mean()
0.7218
Robust Regression¶
fig
fig
with pm.Model() as ols_model:
# alpha is the slope and beta is the intercept
alpha = pm.Uniform('alpha', -100, 100)
beta = pm.Uniform('beta', -100, 100)
# Ordinary least squares assumes that the noise is normally distributed
y_obs = pm.Normal('y_obs', alpha + beta * x, 1., observed=y)
Applied interval-transform to alpha and added transformed alpha_interval to model. Applied interval-transform to beta and added transformed beta_interval to model.
samples = 10000
with ols_model:
step = pm.Metropolis()
ols_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 10000 of 10000 complete in 2.2 sec
post_y = ols_trace['alpha'] + np.outer(plot_X[:, 1], ols_trace['beta'])
fig
fig
with pm.Model() as robust_model:
# alpha is the slope and beta is the intercept
alpha = pm.Uniform('alpha', -100, 100)
beta = pm.Uniform('beta', -100, 100)
# t-distributed residuals are less sensitive to outliers
y_obs = pm.StudentT('y_obs', nu=3., mu=alpha + beta * x, observed=y)
Applied interval-transform to alpha and added transformed alpha_interval to model. Applied interval-transform to beta and added transformed beta_interval to model.
with robust_model:
step = pm.Metropolis()
robust_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 10000 of 10000 complete in 2.3 sec
post_y_robust = robust_trace['alpha'] + np.outer(plot_X[:, 1], robust_trace['beta'])
fig
Congressional Ideal Point Model¶
df.head()
| party | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rep | |||||||||||||||||
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | NaN | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | NaN |
| 2 | 1 | NaN | 1 | 1 | NaN | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 3 | 1 | 0 | 1 | 1 | 0 | NaN | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | NaN | 1 | 1 | 1 | 1 |
parties
Index(['republican', 'democrat'], dtype='object')
grid.fig
$p_{i, j}$ is the probability that representative $i$ votes for bill $j$.
$$ \begin{align*} \log \left(\frac{p_{i, j}}{1 - p_{i, j}}\right) & = \gamma_j \left(\alpha_i - \beta_j\right) \\ & = \textrm{ability of bill } j \textrm{ to discriminate} \times (\textrm{conservativity of represetative } i\ - \textrm{conservativity of bill } j) \end{align*} $$with pm.Model() as ideal_point_model:
# The conservativity of representative i
alpha = pm.Normal('alpha', 0, 1., shape=N_REPS)
# The conservativity of bill j
mu_beta = pm.Normal('mu_beta', 0, 1e-3)
sigma_beta = pm.Uniform('sigma_beta', 0, 1e2)
beta = pm.Normal('beta', mu_beta, sd=sigma_beta, shape=N_BILLS)
# The ability of bill j to discriminate
mu_gamma = pm.Normal('mu_gamma', 0, 1e-3)
sigma_gamma = pm.Uniform('sigma_gamma', 0, 1e2)
gamma = pm.Normal('gamma', mu_gamma, sd=sigma_gamma, shape=N_BILLS)
# The probability that representative i votes for bill j
p = pm.Deterministic('p', T.nnet.sigmoid(gamma[vote_df.bill] * (alpha[vote_df.rep] - beta[vote_df.bill])))
# The observed votes
vote = pm.Bernoulli('vote', p, observed=vote_df.vote)
Applied interval-transform to sigma_beta and added transformed sigma_beta_interval to model. Applied interval-transform to sigma_gamma and added transformed sigma_gamma_interval to model.
samples = 20000
with ideal_point_model:
step = pm.Metropolis()
ideal_point_trace = pm.sample(samples, step, random_seed=SEED)
[-----------------100%-----------------] 20000 of 20000 complete in 107.5 sec
rep_alpha = ideal_point_trace['alpha'].mean(axis=0)
fig
pm.forestplot(ideal_point_trace, varnames=['gamma']);

Source: http://mqscores.berkeley.edu/
References¶
Probabilistic Programming and Bayesian Methods for Hackers (Open source, uses PyMC2, PyMC3 port in progress)
Think Bayes (Available freely online, calculations in Python)