#!/usr/bin/env python
# coding: utf-8
# In[1]:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (12,5)
# Для кириллицы на графиках
font = {'family': 'Verdana',
'weight': 'normal'}
plt.rc('font', **font)
# # Майнор по Анализу Данных, Группа ИАД-2
# ## 10/04/2017 Отбор признаков и понижение размерности
# # Проклятье размености
#
# 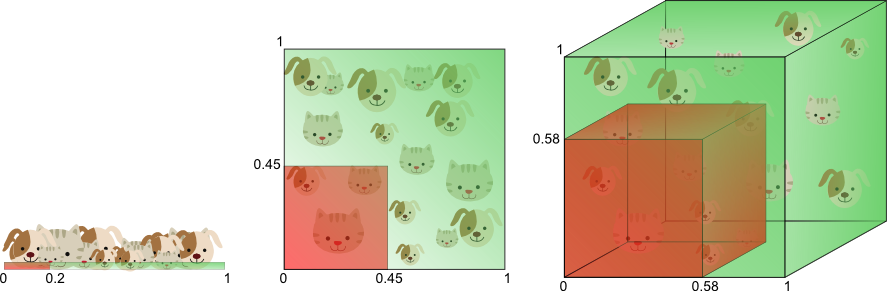 # ## Способы понижения размерности
#
# Избавляться от размерности можно методами **отбора признаков (Feature Selection)** и методами **уменьшения размерности (Feature Reduction)**
# ### Feature Selection
# Методы деляться на три группы:
# * Filter methods
# * Признаки рассматриваются независимо друг от друга
# * Изучается индивидуальный "вклад" призника в предсказываемую переменную
# * Быстрое вычисление
# * Wrapper methods
# * Идет отбор группы признаков
# * Может быть оооочень медленным, но качество, обычно, лучше чем у Filter Methods
# * Embedded methods
# * Отбор признаков "зашит" в модель
# * *Пример?*
# ### Filter method - Mutual Information
# $$MI(y,x) = \sum_{x,y} p(x,y) \ln\left[\frac{p(x,y)}{p(x)p(y)}\right]$$
# Сколько информации $x$ сообщает об $y$.
# $$NormalizedMI(y,x) = \frac{MI(y,x)}{H(y)}$$
# Загрузим довольно известный набор данных о выживаемости после катастрофы титаника.
# In[2]:
df_titanic = pd.read_csv('titanic.csv')
df_titanic.head()
# In[44]:
pd.crosstab(df_titanic.Survived, df_titanic.Sex, normalize=True, )
# Найдем MI между выживаемостью и остальными признаками
# In[41]:
def calc_mutual_information(y, x):
P = pd.crosstab(x, y, normalize=True).values
logP = np.log(((P/P.sum(axis=0)).T/P.sum(axis=1)).T)
return (P*logP).sum()
# In[47]:
calc_mutual_information(df_titanic.Survived, df_titanic.Sex)
# In[26]:
from sklearn.metrics import mutual_info_score
from sklearn.metrics import normalized_mutual_info_score
# In[48]:
mutual_info_score(df_titanic.Survived, df_titanic.Sex)
# ### Wrapper Methods - Recursive Feature Elimination
#
# При данном подходе из (линейной) модели последовательно удаляются признаки с наименьшим коэффициентом
#
# Используйте реализацию RFE в sklean c кросс-валидацией.
#
# * Обучите модель
# * Выведите на графике размер признакового пространства и полученное качество
# * Выведите веса признаков в выбранном признаковом пространстве
# In[49]:
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import RFECV
from sklearn.model_selection import StratifiedKFold
# In[50]:
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=123)
# In[51]:
def titanic_preproc(df_input):
df = df_input.copy()
# Удаляем пропуски
df = df.dropna()
# Создаем такой признак
df.loc[:, 'has_cabin'] = df.loc[:, 'Cabin'].isnull().astype(int)
# Удаляем колонки
cols2drop = ['PassengerId', 'Name', 'Ticket', 'Cabin']
df = df.drop(cols2drop, axis=1)
# Нормализуем Age Fare и SibSp (Так делать не оч хорошо)
df.loc[:, 'Age'] = (df.loc[:, 'Age'] - df.loc[:, 'Age'].mean())/df.loc[:, 'Age'].std()
df.loc[:, 'Fare'] = (df.loc[:, 'Fare'] - df.loc[:, 'Fare'].mean())/df.loc[:, 'Fare'].std()
df.loc[:, 'SibSp'] = (df.loc[:, 'SibSp'] - df.loc[:, 'SibSp'].mean())/df.loc[:, 'SibSp'].std()
# Закодируем поле Sex
df.loc[:, 'Sex'] = df.loc[:, 'Sex'].replace({'male': 0, 'female':1})
# Pclass и Embarked можно рассматривать как категориальный признак
df = pd.get_dummies(df, prefix_sep='=', columns=['Pclass', 'Embarked'], drop_first=True)
return df
# In[61]:
df_prep.head()
# In[52]:
df_prep = df_titanic.pipe(titanic_preproc)
X, y = df_prep.iloc[:, 1:].values, df_prep.iloc[:, 0].values
# In[53]:
model = LogisticRegression(random_state=123)
rfe = RFECV(model, step=1, cv=cv, scoring='roc_auc', verbose=1, n_jobs=-1)
# In[54]:
rfe.fit(X, y)
# In[55]:
rfe.grid_scores_
# In[59]:
d = rfe.grid_scores_.shape[0]
plt.plot(range(1, d+1), rfe.grid_scores_)
plt.xlabel('number of features')
plt.ylabel('ROC-AUC cv')
# In[62]:
print 'Выбранные признаки'
fnames = df_prep.columns[1:].values
fnames[rfe.support_]
# In[66]:
pd.Series(index=fnames[rfe.support_], data=rfe.estimator_.coef_[0])
# ### Embedded methods
# * Обучите случайный лес на данных
# * Выведите важность признаков и сравните с выдачей по Filter и Wrapper подходам
# In[ ]:
## Your code here
# # Principal Component Analysis
# ## Метод Главных Компонент
# # PCA
#
# * Позволяет уменьшить число переменных, выбрав самые изменчивые из них
# * Новые переменные являются линейной комбинацией старых переменных
# * Переход к ортономированному базису
#
#
# ## Способы понижения размерности
#
# Избавляться от размерности можно методами **отбора признаков (Feature Selection)** и методами **уменьшения размерности (Feature Reduction)**
# ### Feature Selection
# Методы деляться на три группы:
# * Filter methods
# * Признаки рассматриваются независимо друг от друга
# * Изучается индивидуальный "вклад" призника в предсказываемую переменную
# * Быстрое вычисление
# * Wrapper methods
# * Идет отбор группы признаков
# * Может быть оооочень медленным, но качество, обычно, лучше чем у Filter Methods
# * Embedded methods
# * Отбор признаков "зашит" в модель
# * *Пример?*
# ### Filter method - Mutual Information
# $$MI(y,x) = \sum_{x,y} p(x,y) \ln\left[\frac{p(x,y)}{p(x)p(y)}\right]$$
# Сколько информации $x$ сообщает об $y$.
# $$NormalizedMI(y,x) = \frac{MI(y,x)}{H(y)}$$
# Загрузим довольно известный набор данных о выживаемости после катастрофы титаника.
# In[2]:
df_titanic = pd.read_csv('titanic.csv')
df_titanic.head()
# In[44]:
pd.crosstab(df_titanic.Survived, df_titanic.Sex, normalize=True, )
# Найдем MI между выживаемостью и остальными признаками
# In[41]:
def calc_mutual_information(y, x):
P = pd.crosstab(x, y, normalize=True).values
logP = np.log(((P/P.sum(axis=0)).T/P.sum(axis=1)).T)
return (P*logP).sum()
# In[47]:
calc_mutual_information(df_titanic.Survived, df_titanic.Sex)
# In[26]:
from sklearn.metrics import mutual_info_score
from sklearn.metrics import normalized_mutual_info_score
# In[48]:
mutual_info_score(df_titanic.Survived, df_titanic.Sex)
# ### Wrapper Methods - Recursive Feature Elimination
#
# При данном подходе из (линейной) модели последовательно удаляются признаки с наименьшим коэффициентом
#
# Используйте реализацию RFE в sklean c кросс-валидацией.
#
# * Обучите модель
# * Выведите на графике размер признакового пространства и полученное качество
# * Выведите веса признаков в выбранном признаковом пространстве
# In[49]:
from sklearn.linear_model import LogisticRegression
from sklearn.feature_selection import RFECV
from sklearn.model_selection import StratifiedKFold
# In[50]:
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=123)
# In[51]:
def titanic_preproc(df_input):
df = df_input.copy()
# Удаляем пропуски
df = df.dropna()
# Создаем такой признак
df.loc[:, 'has_cabin'] = df.loc[:, 'Cabin'].isnull().astype(int)
# Удаляем колонки
cols2drop = ['PassengerId', 'Name', 'Ticket', 'Cabin']
df = df.drop(cols2drop, axis=1)
# Нормализуем Age Fare и SibSp (Так делать не оч хорошо)
df.loc[:, 'Age'] = (df.loc[:, 'Age'] - df.loc[:, 'Age'].mean())/df.loc[:, 'Age'].std()
df.loc[:, 'Fare'] = (df.loc[:, 'Fare'] - df.loc[:, 'Fare'].mean())/df.loc[:, 'Fare'].std()
df.loc[:, 'SibSp'] = (df.loc[:, 'SibSp'] - df.loc[:, 'SibSp'].mean())/df.loc[:, 'SibSp'].std()
# Закодируем поле Sex
df.loc[:, 'Sex'] = df.loc[:, 'Sex'].replace({'male': 0, 'female':1})
# Pclass и Embarked можно рассматривать как категориальный признак
df = pd.get_dummies(df, prefix_sep='=', columns=['Pclass', 'Embarked'], drop_first=True)
return df
# In[61]:
df_prep.head()
# In[52]:
df_prep = df_titanic.pipe(titanic_preproc)
X, y = df_prep.iloc[:, 1:].values, df_prep.iloc[:, 0].values
# In[53]:
model = LogisticRegression(random_state=123)
rfe = RFECV(model, step=1, cv=cv, scoring='roc_auc', verbose=1, n_jobs=-1)
# In[54]:
rfe.fit(X, y)
# In[55]:
rfe.grid_scores_
# In[59]:
d = rfe.grid_scores_.shape[0]
plt.plot(range(1, d+1), rfe.grid_scores_)
plt.xlabel('number of features')
plt.ylabel('ROC-AUC cv')
# In[62]:
print 'Выбранные признаки'
fnames = df_prep.columns[1:].values
fnames[rfe.support_]
# In[66]:
pd.Series(index=fnames[rfe.support_], data=rfe.estimator_.coef_[0])
# ### Embedded methods
# * Обучите случайный лес на данных
# * Выведите важность признаков и сравните с выдачей по Filter и Wrapper подходам
# In[ ]:
## Your code here
# # Principal Component Analysis
# ## Метод Главных Компонент
# # PCA
#
# * Позволяет уменьшить число переменных, выбрав самые изменчивые из них
# * Новые переменные являются линейной комбинацией старых переменных
# * Переход к ортономированному базису
#
# 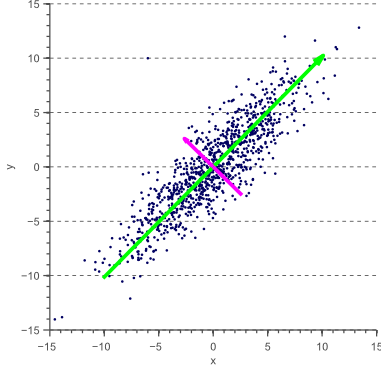 # ## FYI (Посмотрите дома, если интересно)
# ### Построение PCA
# * Пусть $x \in \mathbb{R}^d$ - вектор признаков для какого-то объекта. Будем считать, что $x$ - центрировано и отшкалировано. $E[x_i] = 0, V[x_i] = 1, \quad i=1 \dots d$
# * Требуется найти линейное преобразование, которое задается ортогональной матрицей $A$:
# $$ pc = A^\top x $$
#
# * $pc_i = a_i^\top x = x^\top a_i$
# * $cov[x] = E[(x - E[x])(x - E[x])^\top] = Exx^\top = \Sigma$ - ковариационная матрица
# * $E[pc_i] = E[a_i^\top x] = a_i^\top E[x]$
# * $cov[pc_i, pc_j] = E[pc_i \cdot pc_j^\top] = a_i^\top \Sigma a_j $
# * $\Sigma$ - симметричная и положительно определенная матрица.
# * Собственные числа $\lambda_i \in \mathbb{R}, \lambda_i \geq 0$ (Будем считать, что $\lambda_1 > \lambda_2 > \dots > \lambda_d $
# * Собственные вектора при $\lambda_i \neq \lambda_j $ ортогональны: $v_i^\top v_j = 0$
# * У каждого $\lambda_i$ есть единственный $v_i$
# ### Первая компонента
# $$ pc_1 = a_1 ^\top x $$
#
# \begin{equation}
# \begin{cases}
# V[pc_1] = a_1^\top \Sigma a_1 \rightarrow \max_a \\
# a_1^\top a_1 = 1
# \end{cases}
# \end{equation}
# * Строим функцию лагранжа
# $$ \mathcal{L}(a_1, \nu) = a_1^\top \Sigma a_1 - \nu (a_1^\top a_1 - 1) \rightarrow max_{a_1, \nu}$$
# * Считаем производую по $a_1$
# $$ \frac{\partial\mathcal{L}}{\partial a_1} = 2\Sigma a_1 - 2\nu a_1 = 0 $$
# * Получается, что $a_1$ один из собственных векторов матрицы $\Sigma$, причем при $\lambda_1$
# $$ V[pc_1] = a_1^\top \Sigma a_1 = \lambda_i a_1^\top a_1 = \lambda_i $$
# ### Вторая компонента
# $$ pc_2 = a_2 ^\top x $$
#
# \begin{equation}
# \begin{cases}
# V[pc_1] = a_2^\top \Sigma a_2 \rightarrow \max_a \\
# a_2^\top a_2 = 1 \\
# cov[pc_1, pc_2] = a_2^\top \Sigma a_1 = \lambda_1 a_2^\top a_1 = 0
# \end{cases}
# \end{equation}
# * Строим функцию лагранжа
# $$ \mathcal{L}(a_2, \nu, \tau) = a_2^\top \Sigma a_2 - \nu (a_2^\top a_2 - 1) - \tau a_2^\top a_1 \rightarrow max_{a_1, \nu}$$
#
# Аналогичными выкладками приходим к тому, что $a_2$ - собственный вектор $\Sigma$ при $\lambda_2$
# ## Singular Value Decomposition
#
# Для любой матрицы $X$ размера $n \times m$ можно найти разложение вида:
# $$ X = U S V^\top ,$$
# где
# * $U$ - унитарная матрица, состоящая из собственных векторов $XX^\top$
# * $V$ - унитарная матрица, состоящая из собственных векторов $X^\top X$
# * $S$ - диагональная матрица с сингулярными числами $s_i = \sqrt{\lambda_i}$
# Матрицы $U$ и $V$ ортогональны и могут быть использованы для перехода к ортогональному базису:
# $$ XV = US$$
#
# Сокращение размерности заключается в том, что вместо того, чтобы умножать $X$ на всю матрицу $V$, а лишь на первые $k
# ## FYI (Посмотрите дома, если интересно)
# ### Построение PCA
# * Пусть $x \in \mathbb{R}^d$ - вектор признаков для какого-то объекта. Будем считать, что $x$ - центрировано и отшкалировано. $E[x_i] = 0, V[x_i] = 1, \quad i=1 \dots d$
# * Требуется найти линейное преобразование, которое задается ортогональной матрицей $A$:
# $$ pc = A^\top x $$
#
# * $pc_i = a_i^\top x = x^\top a_i$
# * $cov[x] = E[(x - E[x])(x - E[x])^\top] = Exx^\top = \Sigma$ - ковариационная матрица
# * $E[pc_i] = E[a_i^\top x] = a_i^\top E[x]$
# * $cov[pc_i, pc_j] = E[pc_i \cdot pc_j^\top] = a_i^\top \Sigma a_j $
# * $\Sigma$ - симметричная и положительно определенная матрица.
# * Собственные числа $\lambda_i \in \mathbb{R}, \lambda_i \geq 0$ (Будем считать, что $\lambda_1 > \lambda_2 > \dots > \lambda_d $
# * Собственные вектора при $\lambda_i \neq \lambda_j $ ортогональны: $v_i^\top v_j = 0$
# * У каждого $\lambda_i$ есть единственный $v_i$
# ### Первая компонента
# $$ pc_1 = a_1 ^\top x $$
#
# \begin{equation}
# \begin{cases}
# V[pc_1] = a_1^\top \Sigma a_1 \rightarrow \max_a \\
# a_1^\top a_1 = 1
# \end{cases}
# \end{equation}
# * Строим функцию лагранжа
# $$ \mathcal{L}(a_1, \nu) = a_1^\top \Sigma a_1 - \nu (a_1^\top a_1 - 1) \rightarrow max_{a_1, \nu}$$
# * Считаем производую по $a_1$
# $$ \frac{\partial\mathcal{L}}{\partial a_1} = 2\Sigma a_1 - 2\nu a_1 = 0 $$
# * Получается, что $a_1$ один из собственных векторов матрицы $\Sigma$, причем при $\lambda_1$
# $$ V[pc_1] = a_1^\top \Sigma a_1 = \lambda_i a_1^\top a_1 = \lambda_i $$
# ### Вторая компонента
# $$ pc_2 = a_2 ^\top x $$
#
# \begin{equation}
# \begin{cases}
# V[pc_1] = a_2^\top \Sigma a_2 \rightarrow \max_a \\
# a_2^\top a_2 = 1 \\
# cov[pc_1, pc_2] = a_2^\top \Sigma a_1 = \lambda_1 a_2^\top a_1 = 0
# \end{cases}
# \end{equation}
# * Строим функцию лагранжа
# $$ \mathcal{L}(a_2, \nu, \tau) = a_2^\top \Sigma a_2 - \nu (a_2^\top a_2 - 1) - \tau a_2^\top a_1 \rightarrow max_{a_1, \nu}$$
#
# Аналогичными выкладками приходим к тому, что $a_2$ - собственный вектор $\Sigma$ при $\lambda_2$
# ## Singular Value Decomposition
#
# Для любой матрицы $X$ размера $n \times m$ можно найти разложение вида:
# $$ X = U S V^\top ,$$
# где
# * $U$ - унитарная матрица, состоящая из собственных векторов $XX^\top$
# * $V$ - унитарная матрица, состоящая из собственных векторов $X^\top X$
# * $S$ - диагональная матрица с сингулярными числами $s_i = \sqrt{\lambda_i}$
# Матрицы $U$ и $V$ ортогональны и могут быть использованы для перехода к ортогональному базису:
# $$ XV = US$$
#
# Сокращение размерности заключается в том, что вместо того, чтобы умножать $X$ на всю матрицу $V$, а лишь на первые $k # ## MNIST PCA
#
#
# ## MNIST PCA
#
#  # ## Игрушечный пример
# In[ ]:
from sklearn.decomposition import PCA
from numpy.linalg import svd
from sklearn.datasets import load_digits
# In[ ]:
C = np.array([[0., -0.7], [1.5, 0.7]])
X = np.dot(np.random.randn(200, 2) + np.array([4, 2]), C)
# In[ ]:
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')
# In[ ]:
pca = PCA(n_components=2)
# In[ ]:
PC = pca.fit_transform(X)
# In[ ]:
coef = pca.components_
coef
# In[ ]:
m = np.mean(X,axis=0)
fig, ax = plt.subplots(1,2)
ax[0].plot([0, coef[0,0]*2]+m[0], [0, coef[0,1]*2]+m[1],'--k')
ax[0].plot([0, coef[1,0]*2]+m[0], [0, coef[1,1]*2]+m[1],'--k')
ax[0].scatter(X[:,0], X[:,1])
ax[0].set_xlabel('$x_1$')
ax[0].set_ylabel('$x_2$')
ax[1].scatter(PC[:,0], PC[:,1])
ax[1].set_xlabel('$pc_1$')
ax[1].set_ylabel('$pc_2$')
ax[0].axis('equal')
ax[1].axis('equal')
# #### Сделаем все тоже самое через SVD
# In[ ]:
## Your Code Here
# ## Чиселки
# In[ ]:
digits = load_digits()
X = digits.images
y = digits.target
# In[ ]:
plt.imshow(X[2,:], cmap='Greys', interpolation='none')
# #### Задание
# * Переведите изображения к формату "матрица объект-признак" (reshape)
# * Выполните PCA c двумя компонентами и изобратите полученные точки на плоскости, раскаживая каждую точку в отдельный цвет в соответствии с `y`
# * Отнормируйте данные, запустите SVD, домножте `X` на нужную матрицу и убедитесь, что у вас получается тот же результат
# In[ ]:
### Your Code Here
# ## Пищевая ценность продуктов
# * Загрузите набор данных о пищевом рационе в разных странах мира `diet.csv`
# * Примените на данных PCA с 2 компонентами
# * Изобразите объекты в сжатом пространстве
# In[ ]:
df = pd.read_csv('diet.csv', sep=';')
# In[ ]:
df = df.dropna(axis=1)
df = df.drop('Energy (kcal/day)', axis=1)
df = df.set_index('Countries')
# In[ ]:
df.head()
# In[ ]:
X = df.values
X = (X - X.mean(axis=0))/X.std(axis=0)
# In[ ]:
## Your Code Here
# * Скорее всего вы обнаружите некоторые выбросы, с этим ничего не поделать - PCA чувствителен к выбросам
# * Удалите объекты-выборосы и повторите процедуру
# * Постарайтесь проинтерпретировать главные компоненты
# In[ ]:
## Your Code Here
# # Bonus: T-distributed stochastic neighbor embedding
# * [Вывод](http://jmlr.csail.mit.edu/papers/volume9/vandermaaten08a/vandermaaten08a.pdf)
# * [Примеры](http://lvdmaaten.github.io/tsne/)
# * [Демо](http://distill.pub/2016/misread-tsne/)
# ## Игрушечный пример
# In[ ]:
from sklearn.decomposition import PCA
from numpy.linalg import svd
from sklearn.datasets import load_digits
# In[ ]:
C = np.array([[0., -0.7], [1.5, 0.7]])
X = np.dot(np.random.randn(200, 2) + np.array([4, 2]), C)
# In[ ]:
plt.scatter(X[:, 0], X[:, 1])
plt.axis('equal')
# In[ ]:
pca = PCA(n_components=2)
# In[ ]:
PC = pca.fit_transform(X)
# In[ ]:
coef = pca.components_
coef
# In[ ]:
m = np.mean(X,axis=0)
fig, ax = plt.subplots(1,2)
ax[0].plot([0, coef[0,0]*2]+m[0], [0, coef[0,1]*2]+m[1],'--k')
ax[0].plot([0, coef[1,0]*2]+m[0], [0, coef[1,1]*2]+m[1],'--k')
ax[0].scatter(X[:,0], X[:,1])
ax[0].set_xlabel('$x_1$')
ax[0].set_ylabel('$x_2$')
ax[1].scatter(PC[:,0], PC[:,1])
ax[1].set_xlabel('$pc_1$')
ax[1].set_ylabel('$pc_2$')
ax[0].axis('equal')
ax[1].axis('equal')
# #### Сделаем все тоже самое через SVD
# In[ ]:
## Your Code Here
# ## Чиселки
# In[ ]:
digits = load_digits()
X = digits.images
y = digits.target
# In[ ]:
plt.imshow(X[2,:], cmap='Greys', interpolation='none')
# #### Задание
# * Переведите изображения к формату "матрица объект-признак" (reshape)
# * Выполните PCA c двумя компонентами и изобратите полученные точки на плоскости, раскаживая каждую точку в отдельный цвет в соответствии с `y`
# * Отнормируйте данные, запустите SVD, домножте `X` на нужную матрицу и убедитесь, что у вас получается тот же результат
# In[ ]:
### Your Code Here
# ## Пищевая ценность продуктов
# * Загрузите набор данных о пищевом рационе в разных странах мира `diet.csv`
# * Примените на данных PCA с 2 компонентами
# * Изобразите объекты в сжатом пространстве
# In[ ]:
df = pd.read_csv('diet.csv', sep=';')
# In[ ]:
df = df.dropna(axis=1)
df = df.drop('Energy (kcal/day)', axis=1)
df = df.set_index('Countries')
# In[ ]:
df.head()
# In[ ]:
X = df.values
X = (X - X.mean(axis=0))/X.std(axis=0)
# In[ ]:
## Your Code Here
# * Скорее всего вы обнаружите некоторые выбросы, с этим ничего не поделать - PCA чувствителен к выбросам
# * Удалите объекты-выборосы и повторите процедуру
# * Постарайтесь проинтерпретировать главные компоненты
# In[ ]:
## Your Code Here
# # Bonus: T-distributed stochastic neighbor embedding
# * [Вывод](http://jmlr.csail.mit.edu/papers/volume9/vandermaaten08a/vandermaaten08a.pdf)
# * [Примеры](http://lvdmaaten.github.io/tsne/)
# * [Демо](http://distill.pub/2016/misread-tsne/)



 # ## MNIST PCA
#
#
# ## MNIST PCA
#
# 