#!/usr/bin/env python
# coding: utf-8

# <!--NOTEBOOK_HEADER-->
# *This notebook contains course material from [CBE20255](https://jckantor.github.io/CBE20255)
# by Jeffrey Kantor (jeff at nd.edu); the content is available [on Github](https://github.com/jckantor/CBE20255.git).
# The text is released under the [CC-BY-NC-ND-4.0 license](https://creativecommons.org/licenses/by-nc-nd/4.0/legalcode),
# and code is released under the [MIT license](https://opensource.org/licenses/MIT).*

# <!--NAVIGATION-->
# < [Bubble and Dew Points for Multicomponent Mixtures](http://nbviewer.jupyter.org/github/jckantor/CBE20255/blob/master/notebooks/07.08-Bubble-and-Dew-Points-for-Multicomponent-Mixtures.ipynb) | [Contents](toc.ipynb) | [Binary Distillation with McCabe-Thiele](http://nbviewer.jupyter.org/github/jckantor/CBE20255/blob/master/notebooks/07.10-Binary-Distillation-with-McCabe-Thiele.ipynb) ><p><a href="https://colab.research.google.com/github/jckantor/CBE20255/blob/master/notebooks/07.09-Isothermal-Flash-and-the-Rachford-Rice-Equation.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a>

# # Isothermal Flash and the Rachford-Rice Equation

# ## Summary
# 
# This [Jupyter notebook](http://jupyter.org/notebook.html) illustrates the use of the Rachford-Rice equation solve the material balances for an isothermal flash of an ideal mixture. The video is used with permission from [learnCheme.com](http://learncheme.ning.com/), a project at the University of Colorado funded by the National Science Foundation and the Shell Corporation.

# ## Derivation of the Rachford-Rice Equation
# 
# The derivation of the Rachford-Rice equation is a relatively straightford application of component material balances and Raoult's law for an ideal solution.

# In[1]:


from IPython.display import YouTubeVideo
YouTubeVideo("ACxOiXWq1SQ",560,315,rel=0)


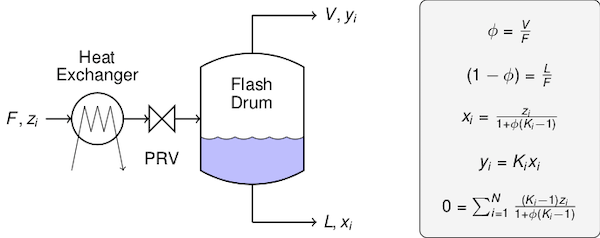
# The quantities, definitions, and equations are summarized in the following figure.
# 
# ![FlashDrumFigure.png](https://raw.githubusercontent.com/jckantor/CBE20255/master/notebooks/figures/FlashDrumFigure.png?raw=true)
# 
# To sketch the derivation, we begin with the overall constraint on the liquid 
# phase and vapor phase mole fractions $x_1 + x_2 + \cdots + x_N = 1$ and $y_1 + y_2 + \cdots + y_N = 1$. Subtracting the first from the second we find
# 
# $$\sum_{n=1}^N (y_n - x_n) = 0$$
# 
# This doesn't look like much, but it turns out to be the essential trick in the development. 
# 
# Next we need expressions for $y_n$ and $x_n$ to substitute into terms in the sum. We get these by solving the component material balance and equilibrium equations for $y_n$ and $x_n$. For each species we write a material balance
# 
# $$L x_n + V y_n = F z_n$$
# 
# Dividing through by the feedrate we get a parameter $\phi = \frac{V}{L}$ denoting the fraction of the feedstream that leaves the flash unit in the vapor stream, the remaining fraction $1-\phi$ leaving in the liquid stream.  With this notation the material balance becomes
# 
# $$(1-\phi)x_n + \phi y_n = z_n$$
# 
# for each species.  
# 
# The second equation is
# 
# $$y_n = K_n x_n$$
# 
# where the 'K-factor' for an ideal solution is given by Raoult's law
# 
# $$K_n = \frac{P_n^{sat}(T)}{P}$$
# 
# The K-factor depends on the operating pressure and temperature of the flash unit. Solving the material balance and equilibrium equations gives
# 
# $$x_n = \frac{z_n}{1 + \phi(K_n - 1)}$$
# 
# $$y_n = \frac{K_n z_n}{1 + \phi(K_n - 1)}$$
# 
# so that the difference $y_n - x_n$ is given by
# 
# $$y_n - x_n = \frac{(K_n - 1)z_n}{1 + \phi(K_n - 1)}$$
# 
# Substitution leads to the Rachford-Rice equation
# 
# $$\sum_{n=1}^{N} \frac{(K_n - 1)z_n}{1 + \phi(K_n - 1)} = 0 $$
# 
# This equation can be used to solve a variety of vapor-liquid equilibrium problems as outline in the following table.

# ## Problem Classification
# 
# | Problem Type | z<sub>i</sub>'s | T       | P       | &phi;   | Action |
# | -----------: | :-----: | :-----: | :-----: | :-----: | :----: |
# | Bubble Point | &check; | unknown | &check; | 0       | Set x<sub>i</sub> = z<sub>i</sub>. Solve for T and y<sub>i</sub>'s |
# | Bubble Point | &check; | &check; | unknown | 0       | Set x<sub>i</sub> = z<sub>i</sub>. Solve for P and y<sub>i</sub>'s |
# | Dew Point    | &check; | unknown | &check; | 1       | Set y<sub>i</sub> = z<sub>i</sub>. Solve for T and x<sub>i</sub>'s |
# | Dew Point    | &check; | &check; | unknown | 1       | Set y<sub>i</sub> = z<sub>i</sub>. Solve for P and x<sub>i</sub>'s |
# | Isothermal Flash | &check; | &check; | &check; | unknown | Solve for &phi;, x<sub>i</sub>'s, and y<sub>i</sub>'s |
# 

# ## Isothermal Flash of a Binary Mixture
# 
# Problem specifications

# In[1]:


import numpy as np
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')


# In[2]:


A = 'acetone'
B = 'ethanol'

P = 760
T = 65

z = dict()
z[A] = 0.6
z[B] = 1 - z[A]


# Compute the K-factors for the given operating conditions

# In[3]:


# Antoine's equations. T [deg C], P [mmHg]
Psat = dict()
Psat[A] = lambda T: 10**(7.02447 - 1161.0/(224 + T))
Psat[B] = lambda T: 10**(8.04494 - 1554.3/(222.65 + T))

# Compute K-factors
K = dict()
K[A] = Psat[A](T)/P
K[B] = Psat[B](T)/P

print("Pressure     {:6.2f} [mmHg]".format(P))
print("Temperature  {:6.2f} [deg C]".format(T))
print("K-factors:")
for n in Psat:
    print("   {:s}  {:7.3f}".format(n,K[n]))


# Rachford-Rice equation

# In[4]:


def RR(phi):
    return (K[A]-1)*z[A]/(1 + phi*(K[A]-1)) + (K[B]-1)*z[B]/(1 + phi*(K[B]-1))

phi = np.linspace(0,1)
plt.plot(phi,[RR(phi) for phi in phi])
plt.xlabel('Vapor Fraction phi')
plt.title('Rachford-Rice Equation')
plt.grid();


# Finding roots of the Rachford-Rice equation

# In[5]:


from scipy.optimize import brentq

phi = brentq(RR,0,1)

print("Vapor Fraction  {:6.4f}".format(phi))
print("Liquid Fraction {:6.4f}".format(1-phi))


# Compositions

# In[6]:


x = dict()
y = dict()

print("Component    z[n]    x[n]    y[n]")

for n in [A,B]:
    x[n] = z[n]/(1 + phi*(K[n]-1))
    y[n] = K[n]*x[n]
    print("{:10s} {:6.4n}  {:6.4f}  {:6.4f}".format(n,z[n],x[n],y[n]))


# ## Multicomponent Mixtures

# In[7]:


P = 760
T = 65

z = dict()
z['acetone'] = 0.6
z['benzene'] = 0.01
z['toluene'] = 0.01
z['ethanol'] = 1 - sum(z.values())


# In[8]:


Psat = dict()
Psat['acetone'] = lambda T: 10**(7.02447 - 1161.0/(224 + T))
Psat['benzene'] = lambda T: 10**(6.89272 - 1203.531/(219.888 + T))
Psat['ethanol'] = lambda T: 10**(8.04494 - 1554.3/(222.65 + T))
Psat['toluene'] = lambda T: 10**(6.95805 - 1346.773/(219.693 + T))

K = {n : lambda P,T,n=n: Psat[n](T)/P for n in Psat}

print("Pressure     {:6.2f} [mmHg]".format(P))
print("Temperature  {:6.2f} [deg C]".format(T))
print("K-factors:")
for n in K:
    print("   {:s}  {:7.3f}".format(n,K[n](P,T)))


# In[9]:


def RR(phi):
    return sum([(K[n](P,T)-1)*z[n]/(1 + phi*(K[n](P,T)-1)) for n in K.keys()])

phi = np.linspace(0,1)
plt.plot(phi,[RR(phi) for phi in phi])
plt.xlabel('Vapor Fraction phi')
plt.title('Rachford-Rice Equation')
plt.grid();


# In[10]:


from scipy.optimize import brentq
 
phi = brentq(RR,0,1)

print("Vapor Fraction  {:6.4f}".format(phi))
print("Liquid Fraction {:6.4f}".format(1-phi))


# In[11]:


x = {n: z[n]/(1 + phi*(K[n](P,T)-1)) for n in z}
y = {n: K[n](P,T)*z[n]/(1 + phi*(K[n](P,T)-1)) for n in z}

print("Component    z[n]    x[n]    y[n]")

for n in z.keys():
    print("{:10s} {:6.4f}  {:6.4f}  {:6.4f}".format(n,z[n],x[n],y[n]))


# [Experiments](http://en.wikipedia.org/wiki/MythBusters_%282005_season%29#Bottle_Rocket_Blast-Off) suggest the bursting pressure of a 2 liter soda bottle is 150 psig. 

# ## Exercises

# ### Design of a Carbonated Beverage
# 
# The purpose of carbonating beverages is to provide a positive pressure inside the package to keep out oxygen and other potential contaminants. The burst pressure of 2 liter soda bottles [has been measured to be 150 psig](http://en.wikipedia.org/wiki/MythBusters_%282005_season%29#Bottle_Rocket_Blast-Off) (approx. 10 atm). For safety, suppose you want the bottle pressure to be no more than 6 atm gauge on a hot summer day in Arizona (say 50 &deg;C, ) and yet have at least 0.5 atm of positive gauge pressure at 0 &deg;C. Assuming your beverage is a mixture of CO<sub>2</sub> and water, is it possible to meet this specification? What concentration (measured in g of CO<sub>2</sub> per g of water) would you recommend?

# In[ ]:





# <!--NAVIGATION-->
# < [Bubble and Dew Points for Multicomponent Mixtures](http://nbviewer.jupyter.org/github/jckantor/CBE20255/blob/master/notebooks/07.08-Bubble-and-Dew-Points-for-Multicomponent-Mixtures.ipynb) | [Contents](toc.ipynb) | [Binary Distillation with McCabe-Thiele](http://nbviewer.jupyter.org/github/jckantor/CBE20255/blob/master/notebooks/07.10-Binary-Distillation-with-McCabe-Thiele.ipynb) ><p><a href="https://colab.research.google.com/github/jckantor/CBE20255/blob/master/notebooks/07.09-Isothermal-Flash-and-the-Rachford-Rice-Equation.ipynb"><img align="left" src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab" title="Open in Google Colaboratory"></a>