#!/usr/bin/env python
# coding: utf-8
# # Focusing Properties of a Binary-Phase Zone Plate
#
# It is also possible to compute a [near-to-far field transformation](https://meep.readthedocs.io/en/latest/Python_User_Interface/#near-to-far-field-spectra) in cylindrical coordinates. This is demonstrated in this example for a binary-phase [zone plate](https://en.wikipedia.org/wiki/Zone_plate) which is a rotationally-symmetric diffractive lens used to focus a normally-incident planewave to a single spot.
#
# Using [scalar theory](http://zoneplate.lbl.gov/theory), the radius of the $n$th zone can be computed as:
#
#
# $$ r_n^2 = n\lambda (f+\frac{n\lambda}{4})$$
#
#
# where $n$ is the zone index (1,2,3,...,$N$), $f$ is the focal length, and $\lambda$ is the operating wavelength. The main design variable is the number of zones $N$. The design specifications of the zone plate are similar to the binary-phase grating in [Tutorial/Mode Decomposition/Diffraction Spectrum of a Binary Grating](https://meep.readthedocs.io/en/latest/Python_Tutorials/Mode_Decomposition/#diffraction-spectrum-of-a-binary-grating) with refractive index of 1.5 (glass), $\lambda$ of 0.5 μm, and height of 0.5 μm. The focusing property of the zone plate is verified by the concentration of the electric-field energy density at the focal length of 0.2 mm (which lies *outside* the cell). The planewave is incident from within a glass substrate and spans the entire length of the cell in the radial direction. The cell is surrounded on all sides by PML. A schematic of the simulation geometry for a design with 25 zones and flat-surface termination is shown below. The near-field line monitor is positioned at the edge of the PML.
#
# 
# In[1]:
import math
import matplotlib.pyplot as plt
import meep as mp
import numpy as np
resolution_um = 25
pml_um = 1.0
substrate_um = 2.0
padding_um = 2.0
height_um = 0.5
focal_length_um = 200
scan_length_z_um = 100
farfield_resolution_um = 10
pml_layers = [mp.PML(thickness=pml_um)]
wavelength_um = 0.5
frequency = 1 / wavelength_um
frequench_width = 0.2 * frequency
# The number of zones in the zone plate.
# Odd-numbered zones impart a π phase shift and
# even-numbered zones impart no phase shift.
num_zones = 25
# Specify the radius of each zone using the equation
# from https://en.wikipedia.org/wiki/Zone_plate.
zone_radius_um = np.zeros(num_zones)
for n in range(1, num_zones + 1):
zone_radius_um[n - 1] = math.sqrt(
n * wavelength_um * (focal_length_um + n * wavelength_um / 4)
)
size_r_um = zone_radius_um[-1] + padding_um + pml_um
size_z_um = pml_um + substrate_um + height_um + padding_um + pml_um
cell_size = mp.Vector3(size_r_um, 0, size_z_um)
# Specify a (linearly polarized) planewave at normal incidence.
sources = [
mp.Source(
mp.GaussianSource(frequency, fwidth=frequench_width, is_integrated=True),
component=mp.Er,
center=mp.Vector3(0.5 * size_r_um, 0, -0.5 * size_z_um + pml_um),
size=mp.Vector3(size_r_um),
),
mp.Source(
mp.GaussianSource(frequency, fwidth=frequench_width, is_integrated=True),
component=mp.Ep,
center=mp.Vector3(0.5 * size_r_um, 0, -0.5 * size_z_um + pml_um),
size=mp.Vector3(size_r_um),
amplitude=-1j,
),
]
glass = mp.Medium(index=1.5)
# Add the substrate.
geometry = [
mp.Block(
material=glass,
size=mp.Vector3(size_r_um, 0, pml_um + substrate_um),
center=mp.Vector3(
0.5 * size_r_um, 0, -0.5 * size_z_um + 0.5 * (pml_um + substrate_um)
),
)
]
# Add the zone plates starting with the ones with largest radius.
for n in range(num_zones - 1, -1, -1):
geometry.append(
mp.Block(
material=glass if n % 2 == 0 else mp.vacuum,
size=mp.Vector3(zone_radius_um[n], 0, height_um),
center=mp.Vector3(
0.5 * zone_radius_um[n],
0,
-0.5 * size_z_um + pml_um + substrate_um + 0.5 * height_um,
),
)
)
sim = mp.Simulation(
cell_size=cell_size,
boundary_layers=pml_layers,
resolution=resolution_um,
sources=sources,
geometry=geometry,
dimensions=mp.CYLINDRICAL,
m=-1,
)
# Add the near-field monitor (must be entirely in air).
n2f_monitor = sim.add_near2far(
frequency,
0,
1,
mp.Near2FarRegion(
center=mp.Vector3(0.5 * (size_r_um - pml_um), 0, 0.5 * size_z_um - pml_um),
size=mp.Vector3(size_r_um - pml_um, 0, 0),
),
mp.Near2FarRegion(
center=mp.Vector3(
size_r_um - pml_um,
0,
0.5 * size_z_um - pml_um - 0.5 * (height_um + padding_um),
),
size=mp.Vector3(0, 0, height_um + padding_um),
),
)
# In[2]:
fig, ax = plt.subplots()
sim.plot2D(ax=ax)
# In[3]:
# Timestep the fields until they have sufficiently decayed away.
sim.run(
until_after_sources=mp.stop_when_fields_decayed(
50.0, mp.Er, mp.Vector3(0.5 * size_r_um, 0, 0), 1e-6
)
)
# In[4]:
farfields_r = sim.get_farfields(
n2f_monitor,
farfield_resolution_um,
center=mp.Vector3(
0.5 * (size_r_um - pml_um),
0,
-0.5 * size_z_um + pml_um + substrate_um + height_um + focal_length_um,
),
size=mp.Vector3(size_r_um - pml_um, 0, 0),
)
farfields_z = sim.get_farfields(
n2f_monitor,
farfield_resolution_um,
center=mp.Vector3(
0, 0, -0.5 * size_z_um + pml_um + substrate_um + height_um + focal_length_um
),
size=mp.Vector3(0, 0, scan_length_z_um),
)
# In[5]:
intensity_r = (
np.absolute(farfields_r["Ex"]) ** 2
+ np.absolute(farfields_r["Ey"]) ** 2
+ np.absolute(farfields_r["Ez"]) ** 2
)
intensity_z = (
np.absolute(farfields_z["Ex"]) ** 2
+ np.absolute(farfields_z["Ey"]) ** 2
+ np.absolute(farfields_z["Ez"]) ** 2
)
# Plot the intensity data and save the result to disk.
fig, ax = plt.subplots(ncols=2)
ax[0].semilogy(np.linspace(0, size_r_um - pml_um, intensity_r.size), intensity_r, "bo-")
ax[0].set_xlim(-2, 20)
ax[0].set_xticks(np.arange(0, 25, 5))
ax[0].grid(True, axis="y", which="both", ls="-")
ax[0].set_xlabel(r"$r$ coordinate (μm)")
ax[0].set_ylabel(r"energy density of far fields, |E|$^2$")
ax[1].semilogy(
np.linspace(
focal_length_um - 0.5 * scan_length_z_um,
focal_length_um + 0.5 * scan_length_z_um,
intensity_z.size,
),
intensity_z,
"bo-",
)
ax[1].grid(True, axis="y", which="both", ls="-")
ax[1].set_xlabel(r"$z$ coordinate (μm)")
ax[1].set_ylabel(r"energy density of far fields, |E|$^2$")
fig.suptitle(f"binary-phase zone plate with focal length $z$ = {focal_length_um} μm")
# Note that the volume specified in `get_farfields` via `center` and `size` is in cylindrical coordinates. These points must therefore lie in the $\phi = 0$ ($rz = xz$) plane. The fields $E$ and $H$ returned by `get_farfields` can be thought of as either cylindrical ($r$,$\phi$,$z$) or Cartesian ($x$,$y$,$z$) coordinates since these are the same in the $\phi = 0$ plane (i.e., $E_r=E_x$ and $E_\phi=E_y$). Also, `get_farfields` tends to gradually *slow down* as the far-field point gets closer to the near-field monitor. This performance degradation is unavoidable and is due to the larger number of $\phi$ integration points required for accurate convergence of the integral involving the Green's function which diverges as the evaluation point approaches the source point.
#
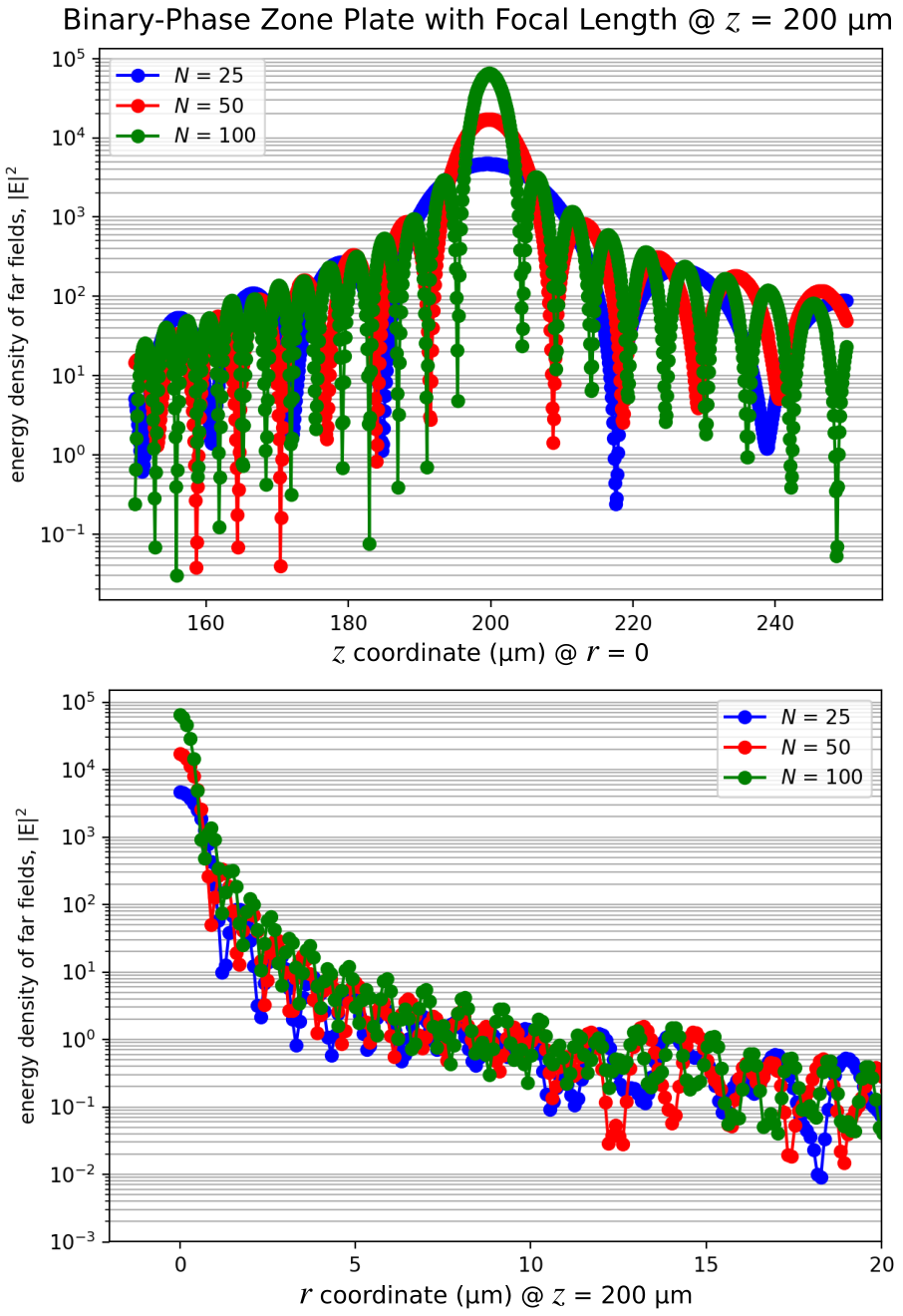
# Shown below is the far-field energy-density profile around the focal length for both the *r* and *z* coordinate directions for three lens designs with $N$ of 25, 50, and 100. The focus becomes sharper with increasing $N$ due to the enhanced constructive interference of the diffracted beam. As the number of zones $N$ increases, the size of the focal spot (full width at half maximum) at $z = 200$ μm decreases as $1/\sqrt{N}$ (see eq. 17 of the [reference](http://zoneplate.lbl.gov/theory)). This means that doubling the resolution (halving the spot width) requires quadrupling the number of zones.
#
#