#!/usr/bin/env python
# coding: utf-8

# <h1 style="text-align:center">Frequency Response to Harmonic Direct-Force Inputs</h1>
# <h3 style="text-align:center">MCHE 485: Mechanical Vibrations</h3> 
# <p style="text-align:center">Dr. Joshua Vaughan <br>
# <a href="mailto:joshua.vaughan@louisiana.edu">joshua.vaughan@louisiana.edu</a><br>
# http://www.ucs.louisiana.edu/~jev9637/   </p>

# <p style="text-align:center">
# 	<img src="http://shared.crawlab.org/MassSpringDamper_DirectForce_Horiz.png" alt="A Mass-Spring-Damper System" width=50%></a><br>
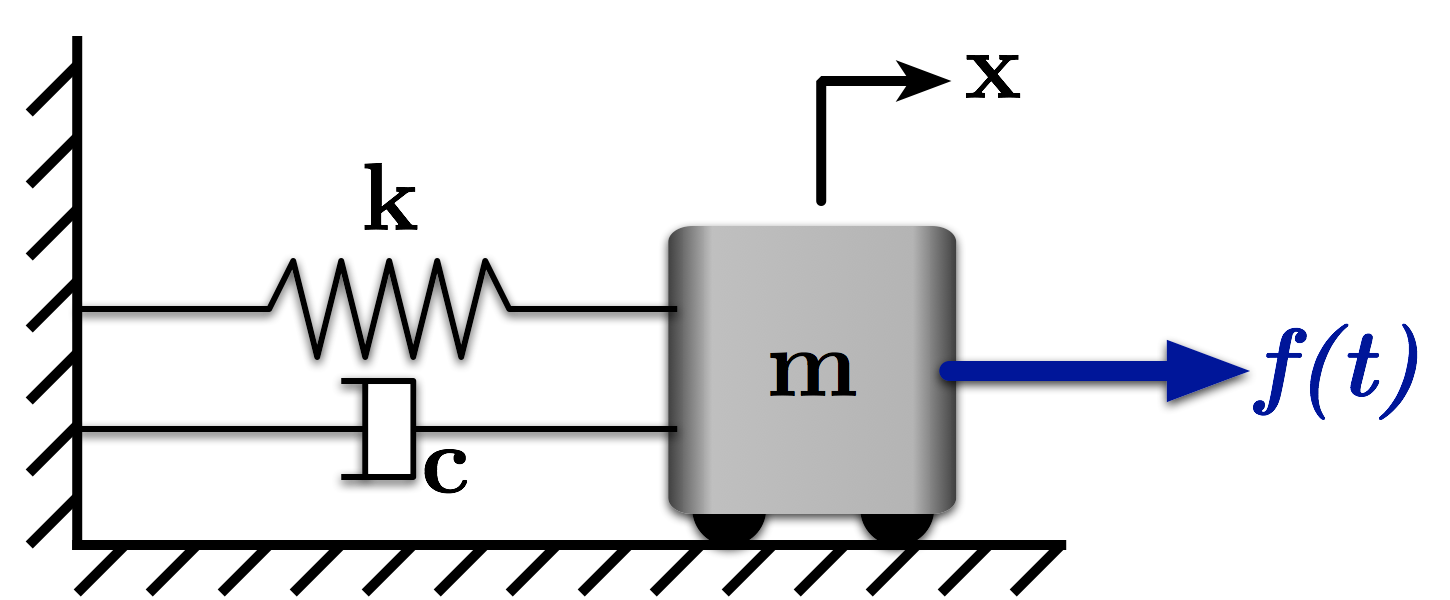
#     <strong> Figure 1: A Mass-Spring-Damper System </strong>
# </p>
# 
# This notebook examines the frequency response of a mass-spring-damper system like the one shown in Figure 1 to a harmonic, direct-force input.
# 
# The equation of motion for the system is:
# 
# <!-- the \quad commmand just adds a space in the math mode -->
# $ \quad m \ddot{x} + c \dot{x} + kx = f $
# 
# We could also write this equation in terms of the damping ratio, $\zeta$, and natural frequency, $\omega_n$.
# 
# $ \quad \ddot{x} + 2\zeta\omega_n \dot{x} + \omega_n^2x = \frac{f}{m}$
# 
# For information on how to obtain this equation, you can see the lectures at the [class website](http://www.ucs.louisiana.edu/~jev9637/MCHE485.html).

# In[1]:


import numpy as np              # Grab all of the NumPy functions with nickname np


# In[2]:


# We want our plots to be displayed inline, not in a separate window
get_ipython().run_line_magic('matplotlib', 'inline')


# In[3]:


# Import the plotting functions 
import matplotlib.pyplot as plt


# In[4]:


# Define the System Parameters
m = 1.0                 # kg
k = (2.0 * np.pi)**2    # N/m (Selected to give an undamped natrual frequency of 1Hz)
wn = np.sqrt(k / m)     # Natural Frequency (rad/s)

z = 0.25                # Define a desired damping ratio
c = 2 * z * wn * m      # calculate the damping coeff. to create it (N/(m/s))


# Let's use the closed-form, steady-state solution we developed in lecture:
# 
# Assume:
# 
# $ \quad f(t) = \bar{f} \sin{\omega t} $
# 
# Then, the solution $x(t)$ should have the form:
# 
# $ \quad x(t) = | x | \sin{\left( \omega t + \phi \right) } $
# 
# Substituting this assumed solution into the equation of motion and solving for $ \bar{x} $ and $ \phi $: 
# 
# $ \quad | \bar{x} | = \frac{\bar{f}}{m} \left( \frac{1}{\sqrt{\left(\omega_n^2 - \omega^2\right)^2 + \left(2 \zeta \omega_n \right)^2}} \right) $
# 
# and
# 
# $ \quad \phi = \tan^{-1}\left({\frac{2 \zeta \omega_n \omega}{\omega_n^2 - \omega^2}}\right) $
# 

# ### Transfer Function Form
# $ \quad \left| G(\omega) \right| = \frac{1}{m \sqrt{\left(\omega_n^2 - \omega^2\right)^2 + \left(2 \zeta \omega_n \right)^2}} $
# 
# ### Normalization
# We can also nondimensionalize/normalize this by defining $ \Omega = \frac{\omega}{\omega_n} $.
# 
# $ \quad \left| G(\Omega) \right| = \frac{1}{k \sqrt{\left(1 - \Omega^2\right)^2 + \left(2 \zeta \Omega \right)^2}} $
# 
# and
# 
# $ \quad \phi = \tan^{-1}\left({\frac{2 \zeta \Omega}{1 - \Omega^2}}\right) $
# 
# Let's plot the normalized versions.

# In[5]:


# Set up input parameters
wun = np.linspace(0,5,500)          # Frequency range for freq response plot, 0-4 Omega with 500 points in-between
w = np.linspace(0,5,500)            # Frequency range for freq response plot, 0-4 Omega with 500 points in-between

# Let's examine a few different damping ratios
z = 0.0
mag_normal_un = 1/(k*np.sqrt((1 - w**2)**2 + (2*z*w)**2))
phase_un = -np.arctan2((2*z*w),(1 - w**2)) * 180/np.pi

# Let's mask the phase discontinuity, so it isn't plotted
pos = np.where(np.abs(k*mag_normal_un) >= 25)
phase_un[pos] = np.nan
wun[pos] = np.nan


z = 0.1
mag_normal_0p1 = 1/(k*np.sqrt((1 - w**2)**2 + (2*z*w)**2))
phase_0p1 = -np.arctan2((2*z*w),(1 - w**2)) * 180/np.pi


z = 0.2
mag_normal_0p2 = 1/(k*np.sqrt((1 - w**2)**2 + (2*z*w)**2))
phase_0p2 = -np.arctan2((2*z*w),(1 - w**2)) * 180/np.pi


z = 0.4
mag_normal_0p4 = 1/(k*np.sqrt((1 - w**2)**2 + (2*z*w)**2))
phase_0p4 = -np.arctan2((2*z*w),(1 - w**2)) * 180/np.pi


# In[6]:


# Let's plot the magnitude (normlized by k G(Omega))

# Make the figure pretty, then plot the results
#   "pretty" parameters selected based on pdf output, not screen output
#   Many of these setting could also be made default by the .matplotlibrc file
fig = plt.figure(figsize=(6,4))
ax = plt.gca()
plt.subplots_adjust(bottom=0.17,left=0.17,top=0.96,right=0.96)
plt.setp(ax.get_ymajorticklabels(),family='Serif',fontsize=18)
plt.setp(ax.get_xmajorticklabels(),family='Serif',fontsize=18)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.grid(True,linestyle=':',color='0.75')
ax.set_axisbelow(True)

plt.xlabel(r'Normalized Frequency ($\Omega$)',family='Serif',fontsize=22,weight='bold',labelpad=5)
plt.ylabel(r'$k |G(\Omega)|$',family='Serif',fontsize=22,weight='bold',labelpad=35)

plt.plot(wun, k*mag_normal_un, linewidth=2, label=r'$\zeta$ = 0.0')
plt.plot(w, k*mag_normal_0p1, linewidth=2, linestyle = '-.', label=r'$\zeta$ = 0.1')
plt.plot(w, k*mag_normal_0p2, linewidth=2, linestyle = ':', label=r'$\zeta$ = 0.2')
plt.plot(w, k*mag_normal_0p4, linewidth=2, linestyle = '--',label=r'$\zeta$ = 0.4')

plt.xlim(0,5)
plt.ylim(0,7)

leg = plt.legend(loc='upper right', fancybox=True)
ltext  = leg.get_texts()
plt.setp(ltext,family='Serif',fontsize=16)

# save the figure as a high-res pdf in the current folder
# plt.savefig('Forced_Freq_Resp_mag.pdf',dpi=300)

fig.set_size_inches(9,6) # Resize the figure for better display in the notebook


# In[7]:


# Now let's plot the phase


# Plot the Phase Response
# Make the figure pretty, then plot the results
#   "pretty" parameters selected based on pdf output, not screen output
#   Many of these setting could also be made default by the .matplotlibrc file
fig = plt.figure(figsize=(6,4))
ax = plt.gca()
plt.subplots_adjust(bottom=0.17,left=0.17,top=0.96,right=0.96)
plt.setp(ax.get_ymajorticklabels(),family='Serif',fontsize=18)
plt.setp(ax.get_xmajorticklabels(),family='Serif',fontsize=18)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.grid(True,linestyle=':',color='0.75')
ax.set_axisbelow(True)

plt.xlabel(r'Normalized Frequency ($\Omega$)',family='Serif',fontsize=22,weight='bold',labelpad=5)
plt.ylabel(r'Phase (deg.)',family='Serif',fontsize=22,weight='bold',labelpad=8)

plt.plot(wun, phase_un, linewidth=2, label=r'$\zeta$ = 0.0')
plt.plot(w, phase_0p1, linewidth=2, linestyle = '-.', label=r'$\zeta$ = 0.1')
plt.plot(w, phase_0p2, linewidth=2, linestyle = ':', label=r'$\zeta$ = 0.2')
plt.plot(w, phase_0p4, linewidth=2, linestyle = '--', label=r'$\zeta$ = 0.4')

plt.xlim(0,5)
plt.ylim(-190,10)
plt.yticks([-180,-90,0])

leg = plt.legend(loc='upper right', fancybox=True)
ltext  = leg.get_texts()
plt.setp(ltext,family='Serif',fontsize=16)

# save the figure as a high-res pdf in the current folder
# plt.savefig('Forced_Freq_Resp_Phase.pdf',dpi=300)

fig.set_size_inches(9,6) # Resize the figure for better display in the notebook


# In[8]:


# Let's plot the magnitude and phase as subplots, to make it easier to compare

# Make the figure pretty, then plot the results
#   "pretty" parameters selected based on pdf output, not screen output
#   Many of these setting could also be made default by the .matplotlibrc file
fig, (ax1, ax2) = plt.subplots(2, 1, sharex = True, figsize=(8,8))

plt.subplots_adjust(bottom=0.12,left=0.17,top=0.96,right=0.96)
plt.setp(ax.get_ymajorticklabels(),family='serif',fontsize=18)
plt.setp(ax.get_xmajorticklabels(),family='serif',fontsize=18)

ax1.spines['right'].set_color('none')
ax1.spines['top'].set_color('none')
ax1.xaxis.set_ticks_position('bottom')
ax1.yaxis.set_ticks_position('left')
ax1.grid(True,linestyle=':',color='0.75')
ax1.set_axisbelow(True)

ax2.spines['right'].set_color('none')
ax2.spines['top'].set_color('none')
ax2.xaxis.set_ticks_position('bottom')
ax2.yaxis.set_ticks_position('left')
ax2.grid(True,linestyle=':',color='0.75')
ax2.set_axisbelow(True)

plt.xlabel(r'Normalized Frequency $\left(\Omega = \frac{\omega}{\omega_n}\right)$',family='serif',fontsize=22,weight='bold',labelpad=5)
plt.xticks([0,1],['0','$\Omega = 1$'])

# Magnitude plot
ax1.set_ylabel(r'$ k|G(\Omega)| $',family='serif',fontsize=22,weight='bold',labelpad=40)
ax1.plot(wun, k*mag_normal_un, linewidth=2, label=r'$\zeta$ = 0.0')
ax1.plot(w, k*mag_normal_0p1, linewidth=2, linestyle = '-.', label=r'$\zeta$ = 0.1')
ax1.plot(w, k*mag_normal_0p2, linewidth=2, linestyle = ':', label=r'$\zeta$ = 0.2')
ax1.plot(w, k*mag_normal_0p4, linewidth=2, linestyle = '--',label=r'$\zeta$ = 0.4')
ax1.set_ylim(0.0,7.0)
ax1.set_yticks([0,1,2,3,4,5],['0', '1'])

ax1.leg = ax1.legend(loc='upper right', fancybox=True)
ltext  = ax1.leg.get_texts()
plt.setp(ltext,family='Serif',fontsize=16)

# Phase plot 
ax2.set_ylabel(r'$ \phi $ (deg)',family='serif',fontsize=22,weight='bold',labelpad=10)
# ax2.plot(wnorm,TFnorm_phase*180/np.pi,linewidth=2)
ax2.plot(wun, phase_un, linewidth=2, label=r'$\zeta$ = 0.0')
ax2.plot(w, phase_0p1, linewidth=2, linestyle = '-.', label=r'$\zeta$ = 0.1')
ax2.plot(w, phase_0p2, linewidth=2, linestyle = ':', label=r'$\zeta$ = 0.2')
ax2.plot(w, phase_0p4, linewidth=2, linestyle = '--', label=r'$\zeta$ = 0.4')
ax2.set_ylim(-200.0,20.0,)
ax2.set_yticks([0, -90, -180])

ax2.leg = ax2.legend(loc='upper right', fancybox=True)
ltext  = ax2.leg.get_texts()
plt.setp(ltext,family='Serif',fontsize=16)

# Adjust the page layout filling the page using the new tight_layout command
plt.tight_layout(pad=0.5)

# If you want to save the figure, uncomment the commands below. 
# The figure will be saved in the same directory as your IPython notebook.
# Save the figure as a high-res pdf in the current folder
# plt.savefig('MassSpring_SeismicTF.pdf',dpi=300)

fig.set_size_inches(9,9) # Resize the figure for better display in the notebook


# <hr style="border: 0px;        height: 1px;        text-align: center;        background: #333;        background-image: -webkit-linear-gradient(left, #ccc, #333, #ccc);        background-image:    -moz-linear-gradient(left, #ccc, #333, #ccc);        background-image:     -ms-linear-gradient(left, #ccc, #333, #ccc);        background-image:      -o-linear-gradient(left, #ccc, #333, #ccc);">

# #### Licenses
# Code is licensed under a 3-clause BSD style license. See the licenses/LICENSE.md file.
# 
# Other content is provided under a [Creative Commons Attribution-NonCommercial 4.0 International License](http://creativecommons.org/licenses/by-nc/4.0/), CC-BY-NC 4.0.

# In[9]:


# This cell will just improve the styling of the notebook
from IPython.core.display import HTML
import urllib.request
response = urllib.request.urlopen("https://cl.ly/1B1y452Z1d35")
HTML(response.read().decode("utf-8"))