#!/usr/bin/env python
# coding: utf-8

# 
# # Bean Stalk Series: Dissecting the E & E3
# #### by D. Koski & K. Urner, May 2018 (version 1.2), last modified Feb 13, 2019
# 
# <br />
# <br />
# 
# <div style="text-align: center">
# <a data-flickr-embed="true"  href="https://www.flickr.com/photos/kirbyurner/37897977156" title="E mod (right tetrahedron) with submodules: Fum, Fo, Fi, Fe going left to right."><img src="https://farm5.staticflickr.com/4444/37897977156_630bb41944_z.jpg" width="640" height="573" alt="E mod (right tetrahedron) with submodules: Fum, Fo, Fi, Fe going left to right."></a><script async src="//embedr.flickr.com/assets/client-code.js" charset="utf-8"></script>
# <div align="center">
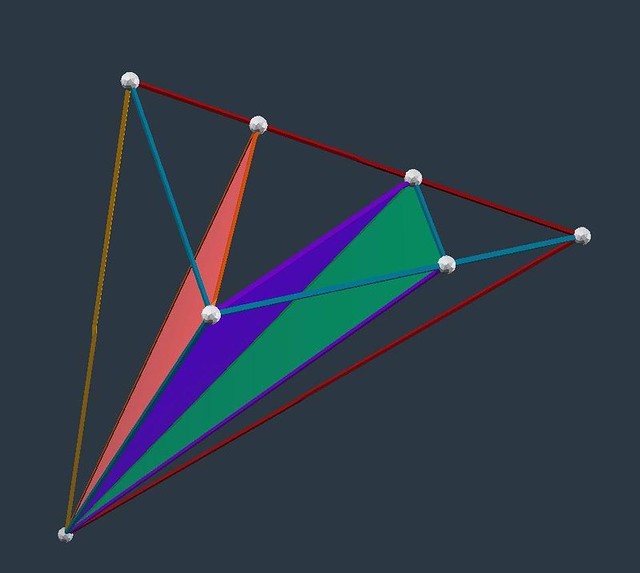
# <b>Figure 1: E3 module dissected into Fum, Fo, Fi and Fe</b>
# </div>
# </div>
# 
# What we see here is another vZome construction by David Koski, showing an E3 module dissected into four sub-modules, according to how the great circles of the 120 LCD Triangles cross the RT as chords.  Compare with [Figure 986.561](http://www.rwgrayprojects.com/synergetics/s09/figs/f86561.html) in Synergetics.
# 
# <div style="text-align: center">
# <a data-flickr-embed="true"  href="https://www.flickr.com/photos/kirbyurner/27606174059/" title="Excerpt from Fig. 986.561, Synergetics 2"><img src="https://farm5.staticflickr.com/4589/27606174059_66f9f02fe8.jpg" width="474" height="390" alt="Excerpt from Fig. 986.561, Synergetics 2"></a><script async src="//embedr.flickr.com/assets/client-code.js" charset="utf-8"></script>
# </div>
# 
# What are their volumes?
# 
# Lets start with E itself.

# In[1]:


import gmpy2
from gmpy2 import sqrt as rt2
from gmpy2 import mpfr
gmpy2.get_context().precision=200

root2 = rt2(mpfr(2))
root3 = rt2(mpfr(3))
root5 = rt2(mpfr(5))

ø = (root5 + 1)/2
ø_down = ø ** -1
ø_up = ø

E_vol = (15 * root2 * ø_down ** 3)/120 # a little more than 1/24, volume of T module
print(E_vol)


# Now lets import the tetravolume.py module, which in turn has dependencies, to get these volumes directly, based on edge lengths.  I'll use the edges given in [Fig. 986.411](http://www.rwgrayprojects.com/synergetics/s09/figs/f86411a.html) of <i>Synergetics</i>, spoking out from the point C at the center of any RT diamond, and/or values computed by David Koski.
# 
# First, lets get a color coded version of the E module...
# <br />
# <br />
# 
# <div style="text-align: center">
# <a data-flickr-embed="true"  href="https://www.flickr.com/photos/kirbyurner/23979124977/in/dateposted-public/" title="LCD Triangles on E mod RT surface"><img src="https://farm5.staticflickr.com/4573/23979124977_506932443c_z.jpg" width="640" height="399" alt="LCD Triangles on E mod RT surface"></a><script async src="//embedr.flickr.com/assets/client-code.js" charset="utf-8"></script>
# <div align="center">
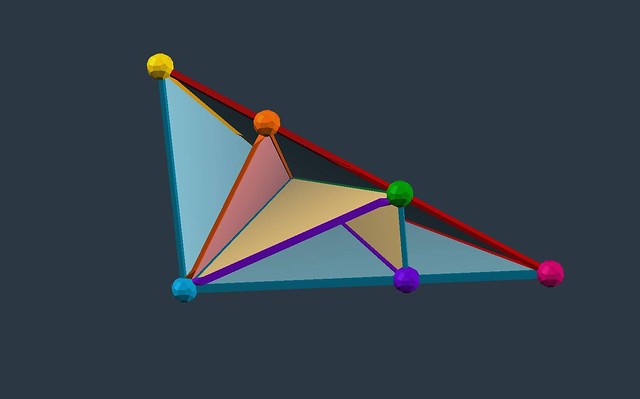
# <b>Figure 2: Dissected E-mod with color-coded vertexes (Koski with vZome)</b>
# </div>
# </div>
# 
# <br />
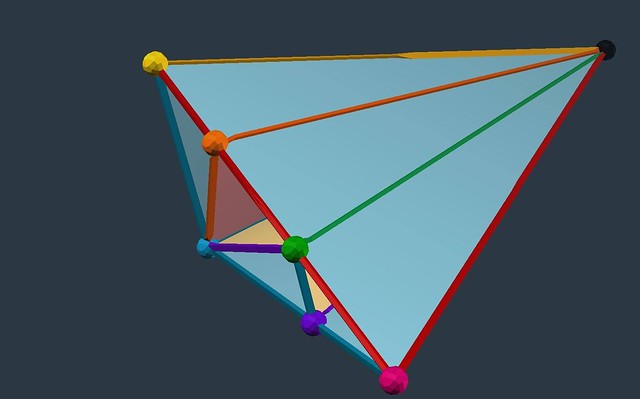
# The black hub is at the center of the RT, as shown here...
# 
# <br />
# 
# <div style="text-align: center">
# <a data-flickr-embed="true"  href="https://www.flickr.com/photos/kirbyurner/24971714468/in/dateposted-public/" title="E module with origin"><img src="https://farm5.staticflickr.com/4516/24971714468_46e14ce4b5_z.jpg" width="640" height="399" alt="E module with origin"></a><script async src="//embedr.flickr.com/assets/client-code.js" charset="utf-8"></script>
# <div style="text-align: center">
# <b>Figure 3: RT center is the black hub (Koski with vZome)</b>
# </div>
# </div>
# 
# <br />
# 
# The edges of the Fum module, tetrahedron Black-Orange-Yellow-Blue will be... (note R=1, D=2):

# In[2]:


# Edges needed for Fum and Emod
e0 = Black_Yellow  = root3 * ø_down
e1 = Black_Blue    = mpfr(1)  # raddfius of RT = 1 (same as unit-radius sphere)
e2 = Black_Orange  = 1/(rt2(ø**2+1)/2)
e3 = Yellow_Blue   = (3 - root5)/2
e4 = Blue_Orange   = (ø**-1)*(1/rt2(ø**2+1))
e5 = Orange_Yellow = rt2(Yellow_Blue**2 - Blue_Orange**2)

e6 = Black_Red  = rt2((5 - root5)/2)
e7 = Blue_Red   = 1/ø
e8 = Red_Yellow = rt2(5 - 2 * root5)

#print(e3 ** 2 + e7 ** 2)
#print(e8 ** 2)
#assert e3 ** 2 + e7 ** 2 == e8 ** 2  # check
#assert e4 ** 2 + e5 ** 2 == e3 ** 2  # check

# not needed for this computation
e9  = Black_Green = 20/(5 * root2 * ø**2) # Sfactor
e10 = Purple_Green = ø ** -4

for e in range(11):
    val = "e" + str(e)
    length = eval(val)
    print("Edge {:3} = {:40.37}".format(val, length))


# In[3]:


import tetravolume as tv # has to be in your path, stored on Github with this JN
# D = 1 in this module, so final volume need to be divided by 8 to match R=1 (D=2)
# see Fig. 986.411A in Synergetics

Fum_vol = tv.Tetrahedron(e0,e1,e2,e3,e4,e5).ivm_volume()/8
E_vol   = tv.Tetrahedron(e1,e0,e6,e3,e8,e7).ivm_volume()/8
print("Fum volume (in tetravolumes): {:40.38}".format( Fum_vol ))
print("E volume (in tetravolumes)  : {:40.38}".format(  E_vol ))


# In[4]:


Fe     = (ø**-7) * (rt2(2)/8)
Fi     = (ø**-6) * (rt2(2)/8)
Fo     = ((5-rt2(5))/5) * (ø**-4) * (rt2(2)/8)
Fum    = (rt2(5)/5) * (ø**-4)*(rt2(2)/8)
Fe_Fi  = (ø**-5) * (rt2(2)/8)
Fo_Fum = (ø**-4) * (rt2(2)/8)
print("Fe:    {:40.38}".format(Fe))
print("Fi:    {:40.38}".format(Fi))
print("Fo:    {:40.38}".format(Fo))
print("Fum:   {:40.38}".format(Fum))
print("E_vol: {:40.38}".format((Fe_Fi) + (Fo_Fum)))
print("E_vol: {:40.38}".format((ø**-3)*(rt2(2)/8)))


# Lets start with a Pentagonal Dodecahedron and build it from Es + e3s.

# In[5]:


PD = 3 * root2 * (ø ** 2 + 1)
print(PD)


# In[6]:


E  = e = E_vol # shorthand (E3 = E * ø_up ** 3, e3 = E * ø_down ** 3, E = e)
e3 = e * ø_down ** 3
PD = 348 * E + 84 * e3
print(PD)


# RT3, on the other hand, has a volume we may express as:

# In[7]:


RT3 = 480 * E + 120 * e3  # e3 is e * ø_down ** 3 (e = E)
print(RT3)


# Recall RT3 is the Rhombic Triacontahedron we get by intersecting the two Platonic duals:  Icosahedron (Icosa) and Pentagonal Dodecahedron (PD), with the former having edges = 2R and volume ~18.51 (5 \* rt2(2) \* ø \*\* 2).
# 
# It turns out that if we shave a Fum3 off an E3, and multiply by 120, we get the PD's volume.
# 
# Put another way: RT3 - PD leaves a volume of 120 Fum3 volumes.  In other words 120 * (E3 - Fum3) = PD.

# In[8]:


E3 = E_vol * ø_up ** 3
Fum3 = Fum_vol * ø_up ** 3
print(E3)
print(Fum3)
print(RT3 - PD)
print(120 * Fum3)


# As you can see, the relationship holds, though floating point numbers add some noise.
# 
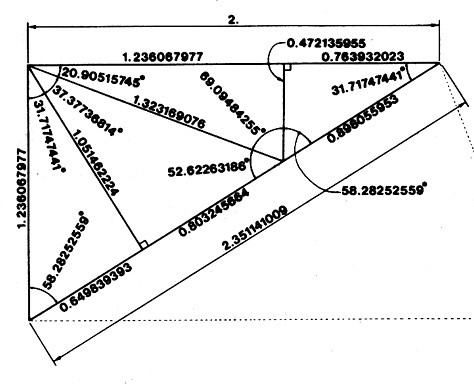
# In addition to edge lengths, we have a succinct way to express the angles of this LCD triangle in terms of ø, thanks to David Koski.

# In[9]:


from math import atan, sqrt as rt2, degrees

Ø = (1 + rt2(5))/2  # back to floating point

print(degrees(atan(Ø**-2)/2))  # 10.812316º
print(degrees(atan(Ø**-3)))    # 13.282525º
print(degrees(atan(Ø**-2)))    # 20.905157º
print(degrees(atan(Ø**-1)))    # 31.717474º
print(degrees(atan(2*Ø**-2)))  # 37.377368º

print(atan(Ø ** -1) + atan(Ø ** -3))
print(atan(1)) # arctan 1 = 45º

print(2 * atan(Ø**-1))
print(atan(2))          # 63.434948º
print(degrees(atan(2))) # 63.434948º

print( atan(Ø**-1) + 3 * atan(Ø**-3) )
print(atan(3))          # 71.565051º
print(degrees(atan(3))) # 71.565051º


# For Further Reading:
# * [Cuboidal E3](https://github.com/4dsolutions/Python5/blob/master/CuboidalE3.ipynb)
# * [Terminology and Scope](http://worldgame.blogspot.com/2017/10/terminology-and-scope.html)
# * [Escaping the Vortex of Standardized Tests](https://medium.com/@kirbyurner/escaping-the-vortex-of-standardized-tests-a-game-plan-84d77d75d100)
# * [S&E Modules (Python 3 Repl)](https://repl.it/@kurner/SandE-Modules)
# * [Figure 986.411A in Synergetics](http://www.rwgrayprojects.com/synergetics/s09/figs/f86411a.html)