
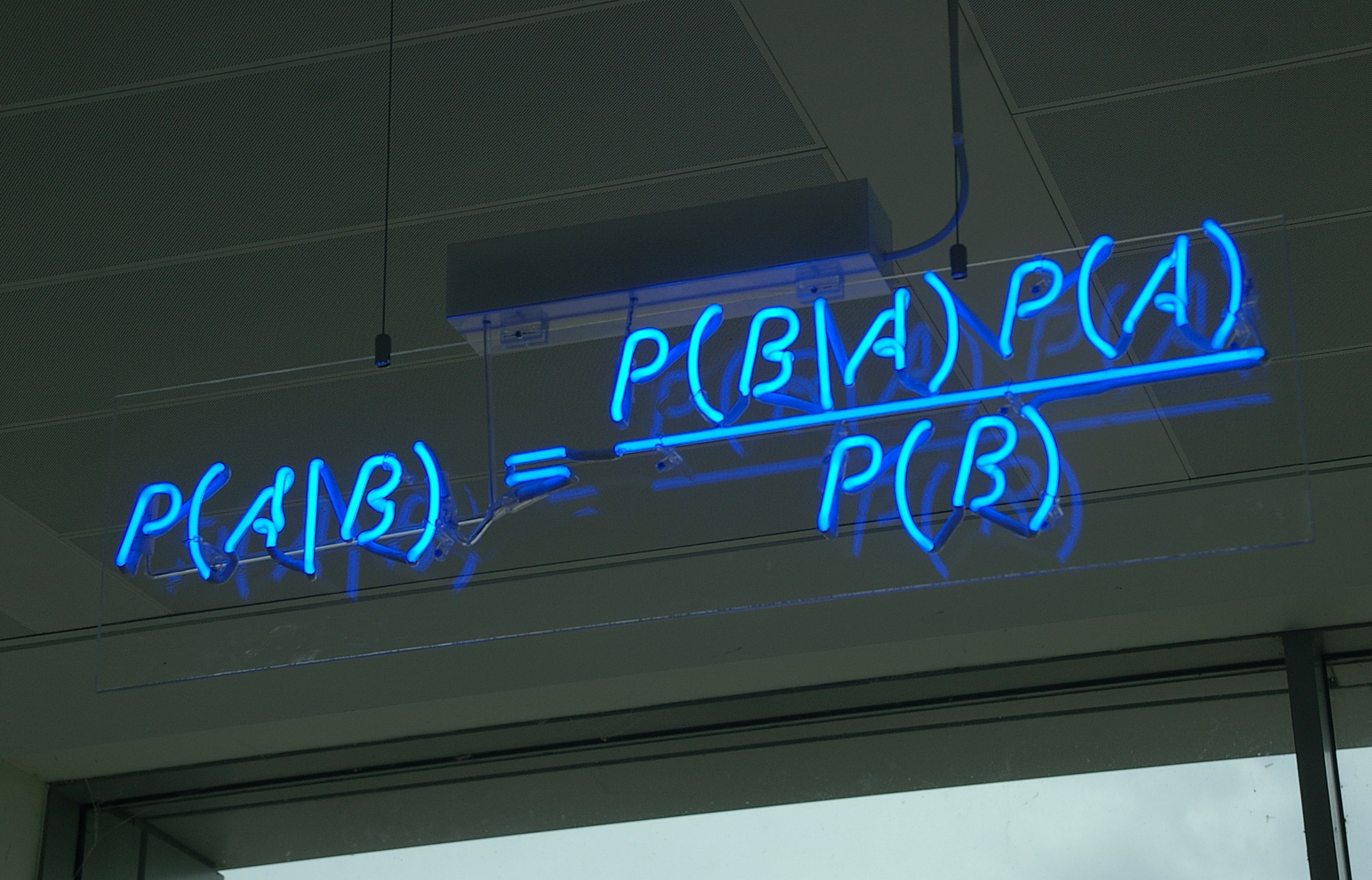 # The posterior distribution is equal to the joint distribution divided by the marginal distribution of the evidence.
#
# $$
# \color{red}{P(\theta\ |\ \mathcal{D})}
# = \frac{\color{blue}{P(\mathcal{D}\ |\ \theta)\ P(\theta)}}{\color{green}{P(\mathcal{D})}}
# = \frac{\color{blue}{P(\mathcal{D}, \theta)}}{\color{green}{\int P(\mathcal{D}\ |\ \theta)\ P(\theta)\ d\theta}}
# $$
#
# For many useful models the marginal distribution of the evidence is **hard or impossible to calculate analytically**.
# ### Modes of Bayesian Inference
#
# * Conjugate models with closed-form posteriors
# * **Markov chain Monte Carlo algorithms**
# * Approximate Bayesian computation
# * Distributional approximations
# * Laplace approximations, INLA
# * **Variational inference**
# ## Markov Chain Monte Carlo Algorithms
#
# * Construct a Markov chain whose stationary distribution is the posterior distribution
# * Sample from the Markov chain for a long time
# * Approximate posterior quantities using the empirical distribution of the samples
# To produce an interesting MCMC animation, we simulate a linear regression data set and animate samples from the posteriors of the regression coefficients.
# In[7]:
x_animation = np.linspace(0, 1, 100)
y_animation = 1 - 2 * x_animation + np.random.normal(0., 0.25, size=100)
# In[8]:
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(x_animation, y_animation,
c=blue);
ax.set_title('MCMC Animation Data Set');
# In[9]:
with pm.Model() as mcmc_animation_model:
intercept = pm.Normal('intercept', 0., 10.)
slope = pm.Normal('slope', 0., 10.)
tau = pm.Gamma('tau', 1., 1.)
y_obs = pm.Normal('y_obs', intercept + slope * x_animation, tau=tau,
observed=y_animation)
animation_trace = pm.sample(5000)
# In[10]:
animation_cov = np.cov(animation_trace['intercept'],
animation_trace['slope'])
animation_sigma, animation_U = np.linalg.eig(animation_cov)
animation_angle = 180. / np.pi * np.arccos(np.abs(animation_U[0, 0]))
# In[11]:
animation_fig = plt.figure()
e = Ellipse((animation_trace['intercept'].mean(), animation_trace['slope'].mean()),
2 * np.sqrt(5.991 * animation_sigma[0]), 2 * np.sqrt(5.991 * animation_sigma[1]),
angle=animation_angle, zorder=5)
e.set_alpha(0.5)
e.set_facecolor(blue)
e.set_zorder(9);
animation_images = [(plt.plot(animation_trace['intercept'][-(iter_ + 1):],
animation_trace['slope'][-(iter_ + 1):],
'-o', c='k', alpha=0.5, zorder=10)[0],)
for iter_ in range(50)]
animation_ax = animation_fig.gca()
animation_ax.add_artist(e);
animation_ax.set_xticklabels([]);
animation_ax.set_xlim(0.75, 1.3);
animation_ax.set_yticklabels([]);
animation_ax.set_ylim(-2.5, -1.5);
mcmc_animation = ArtistAnimation(animation_fig, animation_images,
interval=100, repeat_delay=5000,
blit=True)
mcmc_video = mcmc_animation.to_html5_video()
# In[12]:
HTML(mcmc_video)
# ### Beta-Binomial Model
#
# We observe three successes in ten trials, and want to infer the true success probability.
# In[13]:
x_beta_binomial = np.array([1, 1, 1, 0, 0, 0, 0, 0, 0, 0])
# $$p \sim U(0, 1)$$
# In[14]:
import pymc3 as pm
with pm.Model() as beta_binomial_model:
p_beta_binomial = pm.Uniform('p', 0., 1.)
# $$
# \begin{align*}
# P(X_i = 1\ |\ p)
# & = p
# \end{align*}
# $$
# In[15]:
with beta_binomial_model:
x_obs = pm.Bernoulli('y', p_beta_binomial,
observed=x_beta_binomial)
# $$p\ \left|\ \sum_{i = 1}^{10} X_i \right. = 3 \sim \textrm{Beta}(4, 8)$$
# In[16]:
# plot the true beta-binomial posterior distribution
fig, ax = plt.subplots()
prior = sp.stats.uniform(0, 1)
posterior = sp.stats.beta(1 + x_beta_binomial.sum(), 1 + (1 - x_beta_binomial).sum())
plot_x = np.linspace(0, 1, 100)
ax.plot(plot_x, prior.pdf(plot_x),
'--', c='k', label='Prior');
ax.plot(plot_x, posterior.pdf(plot_x),
c=blue, label='Posterior');
ax.set_xticks(np.linspace(0, 1, 5));
ax.set_xlabel(r'$p$');
ax.set_yticklabels([]);
ax.legend(loc=1);
# In[17]:
fig
# In[18]:
BETA_BINOMIAL_SAMPLES = 50000
BETA_BINOMIAL_BURN = 10000
BETA_BINOMIAL_THIN = 20
# In[19]:
with beta_binomial_model:
beta_binomial_trace_ = pm.sample(BETA_BINOMIAL_SAMPLES, random_seed=SEED)
beta_binomial_trace = beta_binomial_trace_[BETA_BINOMIAL_BURN::BETA_BINOMIAL_THIN]
# In[20]:
bins = np.linspace(0, 1, 50)
ax.hist(beta_binomial_trace['p'], bins=bins, normed=True,
color=green, lw=0., alpha=0.5,
label='MCMC approximate posterior');
ax.legend();
# In[21]:
fig
# #### Pros
#
# * Asymptotically unbiased: converges to the true posterior afer many samples
# * Model-agnostic algorithms
# * Well-studied for more than 60 years
# #### Cons
#
# * Can take a long time to converge
# * Can be difficult to assess convergence
# * Difficult to scale
# ## Variational Inference
#
# * Choose a class of approximating distributions
# * Find the best approximation to the true posterior
# Variational inference minimizes the [Kullback-Leibler divergence](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence)
#
# $$\mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = \mathbb{E}_q\left(\log\left(\frac{\color{purple}{q(\theta)}}{\color{red}{p(\theta\ |\ \mathcal{D})}}\right)\right)$$
#
# from approximate distributons, but we can't calculate the true posterior distribution.
# Minimizing the Kullback-Leibler divergence
#
# $$
# \mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = -(\underbrace{\mathbb{E}_q(\log \color{blue}{p(\mathcal{D}, \theta))} - \mathbb{E}_q(\color{purple}{\log q(\theta)})}_{\color{orange}{\textrm{ELBO}}}) + \log \color{green}{p(\mathcal{D})}
# $$
#
# is equivalent to maximizing the Evidence Lower BOund (ELBO), which only requires calculating the joint distribution.
# ### Variational Inference Example
# In this example, we minimize the Kullback-Leibler divergence between a full-rank covariance Gaussian distribution and a diagonal covariance Gaussian distribution.
# In[22]:
SIGMA_X = 1.
SIGMA_Y = np.sqrt(0.5)
CORR_COEF = 0.75
true_cov = np.array([[SIGMA_X**2, CORR_COEF * SIGMA_X * SIGMA_Y],
[CORR_COEF * SIGMA_X * SIGMA_Y, SIGMA_Y**2]])
true_precision = np.linalg.inv(true_cov)
approx_sigma_x, approx_sigma_y = 1. / np.sqrt(np.diag(true_precision))
# In[23]:
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal');
var, U = np.linalg.eig(true_cov)
angle = 180. / np.pi * np.arccos(np.abs(U[0, 0]))
e = Ellipse(np.zeros(2), 2 * np.sqrt(5.991 * var[0]), 2 * np.sqrt(5.991 * var[1]), angle=angle)
e.set_alpha(0.5)
e.set_facecolor(blue)
e.set_zorder(10);
ax.add_artist(e);
ax.set_xlim(-3, 3);
ax.set_xticklabels([]);
ax.set_ylim(-3, 3);
ax.set_yticklabels([]);
rect = plt.Rectangle((0, 0), 1, 1, fc=blue, alpha=0.5)
ax.legend([rect],
['True distribution'],
bbox_to_anchor=(1.5, 1.));
# In[24]:
fig
# Approximate the true distribution using a diagonal covariance Gaussian from the class
#
# $$\mathcal{Q} = \left\{\left.N\left(\begin{pmatrix} \mu_x \\ \mu_y \end{pmatrix},
# \begin{pmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2\end{pmatrix}\ \right|\
# \mu_x, \mu_y \in \mathbb{R}^2, \sigma_x, \sigma_y > 0\right)\right\}$$
# In[25]:
vi_e = Ellipse(np.zeros(2), 2 * np.sqrt(5.991) * approx_sigma_x, 2 * np.sqrt(5.991) * approx_sigma_y)
vi_e.set_alpha(0.4)
vi_e.set_facecolor(red)
vi_e.set_zorder(11);
ax.add_artist(vi_e);
vi_rect = plt.Rectangle((0, 0), 1, 1, fc=red, alpha=0.75)
ax.legend([rect, vi_rect],
['Posterior distribution',
'Variational approximation'],
bbox_to_anchor=(1.55, 1.));
# In[26]:
fig
# ### Pros
#
# * A principled method to trade complexity for bias
# * Optimization theory is applicable
# * Assesment of convergence
# * Scalability
# ### Cons
#
# * Biased estimate of the true posterior
# * Better for prediction than interpretation
# * Model-specific algorithms
# ### Mean field variational inference
#
# Assume the variational distribution factors independently as $q(\theta_1, \ldots, \theta_n) = q(\theta_1) \cdots q(\theta_n)$
# The variational approximation can be found by **coordinate ascent**
#
# $$
# \begin{align*}
# q(\theta_i)
# & \propto \exp\left(\mathbb{E}_{q_{-i}}(\log(\mathcal{D}, \boldsymbol{\theta}))\right) \\
# q_{-i}(\boldsymbol{\theta})
# & = q(\theta_1) \cdots q(\theta_{i - 1})\ q(\theta_{i + 1}) \cdots q(\theta_n)
# \end{align*}
# $$
#
# #### Coordinate Ascent Cons
#
# * Calculations are tedious, even when possible
# * Convergence is slow when the number of parameters is large
# ## Automating Variational Inference in Python
#
# * Maximize ELBO using gradient ascent instead of coordinate ascent
# * Tensor libraries calculate ELBO gradients automatically
#
# The posterior distribution is equal to the joint distribution divided by the marginal distribution of the evidence.
#
# $$
# \color{red}{P(\theta\ |\ \mathcal{D})}
# = \frac{\color{blue}{P(\mathcal{D}\ |\ \theta)\ P(\theta)}}{\color{green}{P(\mathcal{D})}}
# = \frac{\color{blue}{P(\mathcal{D}, \theta)}}{\color{green}{\int P(\mathcal{D}\ |\ \theta)\ P(\theta)\ d\theta}}
# $$
#
# For many useful models the marginal distribution of the evidence is **hard or impossible to calculate analytically**.
# ### Modes of Bayesian Inference
#
# * Conjugate models with closed-form posteriors
# * **Markov chain Monte Carlo algorithms**
# * Approximate Bayesian computation
# * Distributional approximations
# * Laplace approximations, INLA
# * **Variational inference**
# ## Markov Chain Monte Carlo Algorithms
#
# * Construct a Markov chain whose stationary distribution is the posterior distribution
# * Sample from the Markov chain for a long time
# * Approximate posterior quantities using the empirical distribution of the samples
# To produce an interesting MCMC animation, we simulate a linear regression data set and animate samples from the posteriors of the regression coefficients.
# In[7]:
x_animation = np.linspace(0, 1, 100)
y_animation = 1 - 2 * x_animation + np.random.normal(0., 0.25, size=100)
# In[8]:
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(x_animation, y_animation,
c=blue);
ax.set_title('MCMC Animation Data Set');
# In[9]:
with pm.Model() as mcmc_animation_model:
intercept = pm.Normal('intercept', 0., 10.)
slope = pm.Normal('slope', 0., 10.)
tau = pm.Gamma('tau', 1., 1.)
y_obs = pm.Normal('y_obs', intercept + slope * x_animation, tau=tau,
observed=y_animation)
animation_trace = pm.sample(5000)
# In[10]:
animation_cov = np.cov(animation_trace['intercept'],
animation_trace['slope'])
animation_sigma, animation_U = np.linalg.eig(animation_cov)
animation_angle = 180. / np.pi * np.arccos(np.abs(animation_U[0, 0]))
# In[11]:
animation_fig = plt.figure()
e = Ellipse((animation_trace['intercept'].mean(), animation_trace['slope'].mean()),
2 * np.sqrt(5.991 * animation_sigma[0]), 2 * np.sqrt(5.991 * animation_sigma[1]),
angle=animation_angle, zorder=5)
e.set_alpha(0.5)
e.set_facecolor(blue)
e.set_zorder(9);
animation_images = [(plt.plot(animation_trace['intercept'][-(iter_ + 1):],
animation_trace['slope'][-(iter_ + 1):],
'-o', c='k', alpha=0.5, zorder=10)[0],)
for iter_ in range(50)]
animation_ax = animation_fig.gca()
animation_ax.add_artist(e);
animation_ax.set_xticklabels([]);
animation_ax.set_xlim(0.75, 1.3);
animation_ax.set_yticklabels([]);
animation_ax.set_ylim(-2.5, -1.5);
mcmc_animation = ArtistAnimation(animation_fig, animation_images,
interval=100, repeat_delay=5000,
blit=True)
mcmc_video = mcmc_animation.to_html5_video()
# In[12]:
HTML(mcmc_video)
# ### Beta-Binomial Model
#
# We observe three successes in ten trials, and want to infer the true success probability.
# In[13]:
x_beta_binomial = np.array([1, 1, 1, 0, 0, 0, 0, 0, 0, 0])
# $$p \sim U(0, 1)$$
# In[14]:
import pymc3 as pm
with pm.Model() as beta_binomial_model:
p_beta_binomial = pm.Uniform('p', 0., 1.)
# $$
# \begin{align*}
# P(X_i = 1\ |\ p)
# & = p
# \end{align*}
# $$
# In[15]:
with beta_binomial_model:
x_obs = pm.Bernoulli('y', p_beta_binomial,
observed=x_beta_binomial)
# $$p\ \left|\ \sum_{i = 1}^{10} X_i \right. = 3 \sim \textrm{Beta}(4, 8)$$
# In[16]:
# plot the true beta-binomial posterior distribution
fig, ax = plt.subplots()
prior = sp.stats.uniform(0, 1)
posterior = sp.stats.beta(1 + x_beta_binomial.sum(), 1 + (1 - x_beta_binomial).sum())
plot_x = np.linspace(0, 1, 100)
ax.plot(plot_x, prior.pdf(plot_x),
'--', c='k', label='Prior');
ax.plot(plot_x, posterior.pdf(plot_x),
c=blue, label='Posterior');
ax.set_xticks(np.linspace(0, 1, 5));
ax.set_xlabel(r'$p$');
ax.set_yticklabels([]);
ax.legend(loc=1);
# In[17]:
fig
# In[18]:
BETA_BINOMIAL_SAMPLES = 50000
BETA_BINOMIAL_BURN = 10000
BETA_BINOMIAL_THIN = 20
# In[19]:
with beta_binomial_model:
beta_binomial_trace_ = pm.sample(BETA_BINOMIAL_SAMPLES, random_seed=SEED)
beta_binomial_trace = beta_binomial_trace_[BETA_BINOMIAL_BURN::BETA_BINOMIAL_THIN]
# In[20]:
bins = np.linspace(0, 1, 50)
ax.hist(beta_binomial_trace['p'], bins=bins, normed=True,
color=green, lw=0., alpha=0.5,
label='MCMC approximate posterior');
ax.legend();
# In[21]:
fig
# #### Pros
#
# * Asymptotically unbiased: converges to the true posterior afer many samples
# * Model-agnostic algorithms
# * Well-studied for more than 60 years
# #### Cons
#
# * Can take a long time to converge
# * Can be difficult to assess convergence
# * Difficult to scale
# ## Variational Inference
#
# * Choose a class of approximating distributions
# * Find the best approximation to the true posterior
# Variational inference minimizes the [Kullback-Leibler divergence](https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence)
#
# $$\mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = \mathbb{E}_q\left(\log\left(\frac{\color{purple}{q(\theta)}}{\color{red}{p(\theta\ |\ \mathcal{D})}}\right)\right)$$
#
# from approximate distributons, but we can't calculate the true posterior distribution.
# Minimizing the Kullback-Leibler divergence
#
# $$
# \mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = -(\underbrace{\mathbb{E}_q(\log \color{blue}{p(\mathcal{D}, \theta))} - \mathbb{E}_q(\color{purple}{\log q(\theta)})}_{\color{orange}{\textrm{ELBO}}}) + \log \color{green}{p(\mathcal{D})}
# $$
#
# is equivalent to maximizing the Evidence Lower BOund (ELBO), which only requires calculating the joint distribution.
# ### Variational Inference Example
# In this example, we minimize the Kullback-Leibler divergence between a full-rank covariance Gaussian distribution and a diagonal covariance Gaussian distribution.
# In[22]:
SIGMA_X = 1.
SIGMA_Y = np.sqrt(0.5)
CORR_COEF = 0.75
true_cov = np.array([[SIGMA_X**2, CORR_COEF * SIGMA_X * SIGMA_Y],
[CORR_COEF * SIGMA_X * SIGMA_Y, SIGMA_Y**2]])
true_precision = np.linalg.inv(true_cov)
approx_sigma_x, approx_sigma_y = 1. / np.sqrt(np.diag(true_precision))
# In[23]:
fig, ax = plt.subplots(figsize=(8, 8))
ax.set_aspect('equal');
var, U = np.linalg.eig(true_cov)
angle = 180. / np.pi * np.arccos(np.abs(U[0, 0]))
e = Ellipse(np.zeros(2), 2 * np.sqrt(5.991 * var[0]), 2 * np.sqrt(5.991 * var[1]), angle=angle)
e.set_alpha(0.5)
e.set_facecolor(blue)
e.set_zorder(10);
ax.add_artist(e);
ax.set_xlim(-3, 3);
ax.set_xticklabels([]);
ax.set_ylim(-3, 3);
ax.set_yticklabels([]);
rect = plt.Rectangle((0, 0), 1, 1, fc=blue, alpha=0.5)
ax.legend([rect],
['True distribution'],
bbox_to_anchor=(1.5, 1.));
# In[24]:
fig
# Approximate the true distribution using a diagonal covariance Gaussian from the class
#
# $$\mathcal{Q} = \left\{\left.N\left(\begin{pmatrix} \mu_x \\ \mu_y \end{pmatrix},
# \begin{pmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2\end{pmatrix}\ \right|\
# \mu_x, \mu_y \in \mathbb{R}^2, \sigma_x, \sigma_y > 0\right)\right\}$$
# In[25]:
vi_e = Ellipse(np.zeros(2), 2 * np.sqrt(5.991) * approx_sigma_x, 2 * np.sqrt(5.991) * approx_sigma_y)
vi_e.set_alpha(0.4)
vi_e.set_facecolor(red)
vi_e.set_zorder(11);
ax.add_artist(vi_e);
vi_rect = plt.Rectangle((0, 0), 1, 1, fc=red, alpha=0.75)
ax.legend([rect, vi_rect],
['Posterior distribution',
'Variational approximation'],
bbox_to_anchor=(1.55, 1.));
# In[26]:
fig
# ### Pros
#
# * A principled method to trade complexity for bias
# * Optimization theory is applicable
# * Assesment of convergence
# * Scalability
# ### Cons
#
# * Biased estimate of the true posterior
# * Better for prediction than interpretation
# * Model-specific algorithms
# ### Mean field variational inference
#
# Assume the variational distribution factors independently as $q(\theta_1, \ldots, \theta_n) = q(\theta_1) \cdots q(\theta_n)$
# The variational approximation can be found by **coordinate ascent**
#
# $$
# \begin{align*}
# q(\theta_i)
# & \propto \exp\left(\mathbb{E}_{q_{-i}}(\log(\mathcal{D}, \boldsymbol{\theta}))\right) \\
# q_{-i}(\boldsymbol{\theta})
# & = q(\theta_1) \cdots q(\theta_{i - 1})\ q(\theta_{i + 1}) \cdots q(\theta_n)
# \end{align*}
# $$
#
# #### Coordinate Ascent Cons
#
# * Calculations are tedious, even when possible
# * Convergence is slow when the number of parameters is large
# ## Automating Variational Inference in Python
#
# * Maximize ELBO using gradient ascent instead of coordinate ascent
# * Tensor libraries calculate ELBO gradients automatically
# 
| Direction density calculations #
|
#
 # ## Variational Inference with PyMC3
# ### Automatic Differentiation Variational Inference (ADVI)
#
# * Only applicable to differentiable probability models
# * Transform constrained parameters to be unconstrained
# * Approximate the posterior for unconstrained parameters with mean field Gaussian
# ### Beta-binomial model
# In[57]:
# plot the transformed (unconstrained) parameters
fig, (const_ax, trans_ax) = plt.subplots(ncols=2, figsize=(16, 6))
prior = sp.stats.uniform(0, 1)
posterior = sp.stats.beta(1 + x_beta_binomial.sum(),
1 + (1 - x_beta_binomial).sum())
# constrained distribution plots
const_x = np.linspace(0, 1, 100)
const_ax.plot(const_x, prior.pdf(const_x),
'--', c='k', label='Prior');
def logit_trans_pdf(pdf, x):
x_logit = sp.special.logit(x)
return pdf(x_logit) / (x * (1 - x))
const_ax.plot(const_x, posterior.pdf(const_x),
c=blue, label='Posterior');
const_ax.set_xticks(np.linspace(0, 1, 5));
const_ax.set_xlabel(r'$p$');
const_ax.set_yticklabels([]);
const_ax.set_title('Constrained Parameter Space');
const_ax.legend(loc=1);
# unconstrained distribution plots
def expit_trans_pdf(pdf, x):
x_expit = sp.special.expit(x)
return pdf(x_expit) * x_expit * (1 - x_expit)
trans_x = np.linspace(-5, 5, 100)
trans_ax.plot(trans_x, expit_trans_pdf(prior.pdf, trans_x),
'--', c='k');
trans_ax.plot(trans_x, expit_trans_pdf(posterior.pdf, trans_x),
c=blue);
trans_ax.set_xlim(trans_x.min(), trans_x.max());
trans_ax.set_xlabel(r'$\log\left(\frac{p}{1 - p}\right)$');
trans_ax.set_yticklabels([]);
trans_ax.set_title('Unconstrained Parameter Space');
# #### Transformed distributions
# In[58]:
fig
# In[59]:
get_ipython().run_cell_magic('time', '', 'with beta_binomial_model:\n advi_fit = pm.advi(n=20000, random_seed=SEED)\n')
# In[60]:
advi_bb_mu = advi_fit.means['p_interval_']
advi_bb_std = advi_fit.stds['p_interval_']
advi_bb_dist = sp.stats.norm(advi_bb_mu, advi_bb_std)
# In[61]:
# plot the ADVI gaussian approximation to the unconstrained posterior
trans_ax.plot(trans_x, advi_bb_dist.pdf(trans_x),
c=red, label='Variational approximation');
# #### ADVI approxiation to transformed posterior
# In[62]:
fig
# In[63]:
# plot the ADVI approximation to the true posterior
const_ax.plot(const_x, logit_trans_pdf(advi_bb_dist.pdf, const_x),
c=red, label='Variational approximation');
# #### ADVI approximation to posterior
# In[64]:
fig
# ### Dependent Density Regression
# The depdendent density regression uses LIDAR data from Larry Wasserman's book [_All of Nonparametric Statistics_](http://www.stat.cmu.edu/~larry/all-of-nonpar/).
# In[65]:
get_ipython().run_cell_magic('bash', '', '# download the LIDAR data file, it is not already present\nif [ ! -e /tmp/lidar.dat ]\nthen\n wget -O /tmp/lidar.dat http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/lidar.dat\nfi\n')
# In[66]:
# read and standardize the LIDAR data
lidar_df = (pd.read_csv('/tmp/lidar.dat',
sep=' *', engine='python')
.assign(std_range=lambda df: (df.range - df.range.mean()) / df.range.std(),
std_logratio=lambda df: (df.logratio - df.logratio.mean()) / df.logratio.std()))
# In[67]:
# plot the LIDAR dataset
fig, ax = plt.subplots()
ax.scatter(lidar_df.std_range, lidar_df.std_logratio,
c=blue, zorder=10);
ax.set_xticklabels([]);
ax.set_xlabel('Range');
ax.set_yticklabels([]);
ax.set_ylabel('Log ratio');
ax.set_title('LIDAR Data');
# In[68]:
fig
# _Idea_: A mixture of linear models, where the _unknown number_ of mixture weights depend on $x$
# In[69]:
# fit and plot a few linear models on different intervals
# of the LIDAR data
LIDAR_KNOTS = np.array([-1.75, 0., 0.5, 1.75])
for left_knot, right_knot in zip(LIDAR_KNOTS[:-1], LIDAR_KNOTS[1:]):
between_knots = lidar_df.std_range.between(left_knot, right_knot)
slope, intercept, *_ = sp.stats.linregress(lidar_df.std_range[between_knots].values,
lidar_df.std_logratio[between_knots].values)
knot_plot_x = np.linspace(left_knot - 0.25, right_knot + 0.25, 100)
ax.plot(knot_plot_x, intercept + slope * knot_plot_x,
c=red, lw=2, zorder=100);
ax.set_xlim(-2.1, 2.1);
# In[70]:
fig
# #### Mixture weights
#
# The model has infinitely many mixture components, we truncate to $K$
#
# $$
# \begin{align*}
# \alpha_1, \ldots, \alpha_K
# & \sim N(0, 1) \\
# \beta_1, \ldots, \beta_K
# & \sim N(0, 1) \\
# \boldsymbol{\pi} \ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, x
# & \sim \textrm{Logit-Stick-Breaking}(\boldsymbol{\alpha} + \boldsymbol{\beta} x) \\
# \end{align*}
# $$
# In[71]:
# turn the LIDAR observations into column vectors
# this is important for broadcasting in following
# calculations
std_range = lidar_df.std_range.values[:, np.newaxis]
std_logratio = lidar_df.std_logratio.values[:, np.newaxis]
# The [stick-breaking process](https://en.wikipedia.org/wiki/Dirichlet_process#The_stick-breaking_process) transforms an arbitrary set of values in the interval $[0, 1]$ to a set of weights in $[0, 1]$ that sum to one.
# In[72]:
def stick_breaking(v):
"""
Perform a stick breaking transformation along
the second axis of v
"""
return v * tt.concatenate([tt.ones_like(v[:, :1]),
tt.extra_ops.cumprod(1 - v, axis=1)[:, :-1]],
axis=1)
# In[73]:
K = 20
x_lidar = shared(std_range, broadcastable=(False, True))
with pm.Model() as lidar_model:
alpha = pm.Normal('alpha', 0., 1., shape=K)
beta = pm.Normal('beta', 0., 1., shape=K)
v = tt.nnet.sigmoid(alpha + beta * x_lidar)
pi = pm.Deterministic('pi', stick_breaking(v))
# #### Component linear models
#
# $$
# \begin{align*}
# \gamma_1, \ldots, \gamma_K
# & \sim N(0, 100) \\
# \delta_1, \ldots, \delta_K
# & \sim N(0, 100) \\
# \tau_1, \ldots, \tau_K
# & \sim \textrm{Gamma}(1, 1) \\
# Y_i\ |\ \gamma_i, \delta_i, \tau_i, x
# & \sim N(\gamma_i + \delta_i x, \tau_i^{-1})
# \end{align*}
# $$
# In[74]:
with lidar_model:
gamma = pm.Normal('gamma', 0., 100., shape=K)
delta = pm.Normal('delta', 0., 100., shape=K)
tau = pm.Gamma('tau', 1., 1., shape=K)
ys = pm.Deterministic('ys', gamma + delta * x_lidar)
# #### Observation model
#
# $$
# \begin{align*}
# Y\ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}, \boldsymbol{\delta}, \boldsymbol{\tau}, x
# & = \sum_{i = 1}^K \pi_i Y_i \\
# \end{align*}
# $$
# The `NormalMixture` class is a bit of a hack to marginalize over the categorical indicators that would otherwise be necessary to implement a normal mixture model in PyMC3. This also speeds convergence in both MCMC and variational inference algorithms. See the Stan [_User's Guide and Reference Manual_](http://www.uvm.edu/~bbeckage/Teaching/DataAnalysis/Manuals/stan-reference-2.8.0.pdf) for more information on the benefits of marginalization.
# In[75]:
def normal_mixture_rvs(*args, **kwargs):
w = kwargs['w']
mu = kwargs['mu']
tau = kwargs['tau']
size = kwargs['size']
component = np.array([np.random.choice(w.shape[1], size=size, p=w_ / w_.sum())
for w_ in w])
return sp.stats.norm.rvs(mu[np.arange(w.shape[0]), component], tau[component]**-0.5)
class NormalMixture(pm.distributions.Continuous):
def __init__(self, w, mu, tau, *args, **kwargs):
"""
w is a tesnor of mixture weights
mu is a tensor of the means of the component normal distributions
tau is a tensor of the precisions of the component normal distributions
"""
super(NormalMixture, self).__init__(*args, **kwargs)
self.w = w
self.mu = mu
self.tau = tau
self.mean = (w * mu).sum()
def random(self, point=None, size=None, repeat=None):
"""
Draw a random sample from a normal mixture model
"""
w, mu, tau = draw_values([self.w, self.mu, self.tau], point=point)
return normal_mixture_rvs(w=w, mu=mu, tau=tau, size=size)
def logp(self, value):
"""
The log density of then normal mixture model
"""
w = self.w
mu = self.mu
tau = self.tau
return bound(logsumexp(tt.log(w) + (-tau * (value - mu)**2 + tt.log(tau / np.pi / 2.)) / 2.,
axis=1).sum(),
tau >=0, w >= 0, w <= 1)
# In[76]:
with lidar_model:
lidar_obs = NormalMixture('lidar_obs', pi, ys, tau,
observed=std_logratio)
# #### ADVI inference
# In[77]:
get_ipython().run_cell_magic('time', '', 'N_ADVI_ITER = 50000\n\nwith lidar_model:\n advi_fit = pm.advi(n=N_ADVI_ITER, random_seed=SEED)\n')
# In[78]:
# plot the ELBO over time
fig, ax = plt.subplots()
ax.plot(np.arange(N_ADVI_ITER) + 1, advi_fit.elbo_vals);
ax.set_xlabel('ADVI iteration');
ax.set_ylabel('ELBO');
# In[79]:
fig
# #### Posterior predictions
# In[80]:
PPC_SAMPLES = 5000
lidar_ppc_x = np.linspace(std_range.min() - 0.05,
std_range.max() + 0.05,
100)
with lidar_model:
# sample from the variational posterior distribution
advi_trace = pm.sample_vp(advi_fit, PPC_SAMPLES, random_seed=SEED)
# sample from the posterior predictive distribution
x_lidar.set_value(lidar_ppc_x[:, np.newaxis])
advi_ppc_trace = pm.sample_ppc(advi_trace, PPC_SAMPLES, random_seed=SEED)
# In[81]:
# plot the component mixture weights to assess the impact of truncation
fig, ax = plt.subplots()
ax.bar(np.arange(K) + 1 - 0.4, advi_trace['pi'].mean(axis=0).max(axis=0),
lw=0);
ax.set_xlim(1 - 0.4, K);
ax.set_xlabel('Mixture component');
ax.set_ylabel('Maximum posterior\nexpected mixture weight');
# #### Impact of truncation
# In[82]:
fig
# In[83]:
# plot the posterior predictions for the LIDAR data
fig, ax = plt.subplots()
ax.scatter(lidar_df.std_range, lidar_df.std_logratio,
c=blue, zorder=10);
low, high = np.percentile(advi_ppc_trace['lidar_obs'], [2.5, 97.5], axis=0)
ax.fill_between(lidar_ppc_x, low, high, color='k', alpha=0.35, zorder=5);
ax.plot(lidar_ppc_x, advi_ppc_trace['lidar_obs'].mean(axis=0), c='k', zorder=6);
ax.set_xticklabels([]);
ax.set_xlabel('Range');
ax.set_yticklabels([]);
ax.set_ylabel('Log ratio');
ax.set_title('LIDAR Data');
# In[84]:
fig
# ## References
#
# ### Edward
#
# [edwardlib.org](http://edwardlib.org/)
#
# [Examples](https://github.com/blei-lab/edward/tree/master/examples)
#
# ### PyMC3
#
# [http://pymc-devs.github.io/pymc3/](http://pymc-devs.github.io/pymc3/)
#
# [Examples](http://pymc-devs.github.io/pymc3/examples.html)
#
# PyMC3 port of [_Probabilistic Programming and Bayesian Methods for Hackers_](https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers#pymc3)
# ### Variational Inference
#
# Angelino, Elaine, Matthew James Johnson, and Ryan P. Adams. "[Patterns of Scalable Bayesian Inference](https://arxiv.org/pdf/1602.05221v2.pdf)." arXiv preprint arXiv:1602.05221 (2016).
#
# Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. "[Variational inference: A review for statisticians](http://arxiv.org/pdf/1601.00670)." arXiv preprint arXiv:1601.00670 (2016).
#
# Kucukelbir, Alp, et al. "[Automatic Differentiation Variational Inference](https://arxiv.org/pdf/1603.00788.pdf)." arXiv preprint arXiv:1603.00788 (2016).
#
# Ranganath, Rajesh, Sean Gerrish, and David M. Blei. "[Black Box Variational Inference]((http://www.cs.columbia.edu/~blei/papers/RanganathGerrishBlei2014.pdf)." AISTATS. 2014.
# ### Models
#
# Bafumi, Joseph, et al. "[Practical issues in implementing and understanding Bayesian ideal point estimation](http://www.stat.columbia.edu/~gelman/research/published/171.pdf)." Political Analysis 13.2 (2005): 171-187.
#
# Fox, Jean-Paul. [_Bayesian item response modeling: Theory and applications_](https://www.amazon.com/Bayesian-Item-Response-Modeling-Applications/dp/1441907416). Springer Science & Business Media, 2010.
#
# Gelman, Andrew, et al. [_Bayesian data analysis_](https://www.amazon.com/Bayesian-Analysis-Chapman-Statistical-Science/dp/B00I60M6H6). Vol. 2. Boca Raton, FL, USA: Chapman & Hall/CRC, 2014.
#
# Gelman, Andrew, and Jennifer Hill. [_Data analysis using regression and multilevel/hierarchical models_](https://www.amazon.com/Analysis-Regression-Multilevel-Hierarchical-Models/dp/052168689X). Cambridge University Press, 2006.
#
# Ren, Lu, et al. "[Logistic stick-breaking process](http://www.jmlr.org/papers/volume12/ren11a/ren11a.pdf)." Journal of Machine Learning Research 12.Jan (2011): 203-239.
# ## Thank You!
#
# ### [@AustinRochford](https://twitter.com/AustinRochford) — [Monetate Labs](http://www.monetate.com/)
#
# ### [arochford@monetate.com](mailto:arochford@monetate.com)
#
#
# ## Variational Inference with PyMC3
# ### Automatic Differentiation Variational Inference (ADVI)
#
# * Only applicable to differentiable probability models
# * Transform constrained parameters to be unconstrained
# * Approximate the posterior for unconstrained parameters with mean field Gaussian
# ### Beta-binomial model
# In[57]:
# plot the transformed (unconstrained) parameters
fig, (const_ax, trans_ax) = plt.subplots(ncols=2, figsize=(16, 6))
prior = sp.stats.uniform(0, 1)
posterior = sp.stats.beta(1 + x_beta_binomial.sum(),
1 + (1 - x_beta_binomial).sum())
# constrained distribution plots
const_x = np.linspace(0, 1, 100)
const_ax.plot(const_x, prior.pdf(const_x),
'--', c='k', label='Prior');
def logit_trans_pdf(pdf, x):
x_logit = sp.special.logit(x)
return pdf(x_logit) / (x * (1 - x))
const_ax.plot(const_x, posterior.pdf(const_x),
c=blue, label='Posterior');
const_ax.set_xticks(np.linspace(0, 1, 5));
const_ax.set_xlabel(r'$p$');
const_ax.set_yticklabels([]);
const_ax.set_title('Constrained Parameter Space');
const_ax.legend(loc=1);
# unconstrained distribution plots
def expit_trans_pdf(pdf, x):
x_expit = sp.special.expit(x)
return pdf(x_expit) * x_expit * (1 - x_expit)
trans_x = np.linspace(-5, 5, 100)
trans_ax.plot(trans_x, expit_trans_pdf(prior.pdf, trans_x),
'--', c='k');
trans_ax.plot(trans_x, expit_trans_pdf(posterior.pdf, trans_x),
c=blue);
trans_ax.set_xlim(trans_x.min(), trans_x.max());
trans_ax.set_xlabel(r'$\log\left(\frac{p}{1 - p}\right)$');
trans_ax.set_yticklabels([]);
trans_ax.set_title('Unconstrained Parameter Space');
# #### Transformed distributions
# In[58]:
fig
# In[59]:
get_ipython().run_cell_magic('time', '', 'with beta_binomial_model:\n advi_fit = pm.advi(n=20000, random_seed=SEED)\n')
# In[60]:
advi_bb_mu = advi_fit.means['p_interval_']
advi_bb_std = advi_fit.stds['p_interval_']
advi_bb_dist = sp.stats.norm(advi_bb_mu, advi_bb_std)
# In[61]:
# plot the ADVI gaussian approximation to the unconstrained posterior
trans_ax.plot(trans_x, advi_bb_dist.pdf(trans_x),
c=red, label='Variational approximation');
# #### ADVI approxiation to transformed posterior
# In[62]:
fig
# In[63]:
# plot the ADVI approximation to the true posterior
const_ax.plot(const_x, logit_trans_pdf(advi_bb_dist.pdf, const_x),
c=red, label='Variational approximation');
# #### ADVI approximation to posterior
# In[64]:
fig
# ### Dependent Density Regression
# The depdendent density regression uses LIDAR data from Larry Wasserman's book [_All of Nonparametric Statistics_](http://www.stat.cmu.edu/~larry/all-of-nonpar/).
# In[65]:
get_ipython().run_cell_magic('bash', '', '# download the LIDAR data file, it is not already present\nif [ ! -e /tmp/lidar.dat ]\nthen\n wget -O /tmp/lidar.dat http://www.stat.cmu.edu/~larry/all-of-nonpar/=data/lidar.dat\nfi\n')
# In[66]:
# read and standardize the LIDAR data
lidar_df = (pd.read_csv('/tmp/lidar.dat',
sep=' *', engine='python')
.assign(std_range=lambda df: (df.range - df.range.mean()) / df.range.std(),
std_logratio=lambda df: (df.logratio - df.logratio.mean()) / df.logratio.std()))
# In[67]:
# plot the LIDAR dataset
fig, ax = plt.subplots()
ax.scatter(lidar_df.std_range, lidar_df.std_logratio,
c=blue, zorder=10);
ax.set_xticklabels([]);
ax.set_xlabel('Range');
ax.set_yticklabels([]);
ax.set_ylabel('Log ratio');
ax.set_title('LIDAR Data');
# In[68]:
fig
# _Idea_: A mixture of linear models, where the _unknown number_ of mixture weights depend on $x$
# In[69]:
# fit and plot a few linear models on different intervals
# of the LIDAR data
LIDAR_KNOTS = np.array([-1.75, 0., 0.5, 1.75])
for left_knot, right_knot in zip(LIDAR_KNOTS[:-1], LIDAR_KNOTS[1:]):
between_knots = lidar_df.std_range.between(left_knot, right_knot)
slope, intercept, *_ = sp.stats.linregress(lidar_df.std_range[between_knots].values,
lidar_df.std_logratio[between_knots].values)
knot_plot_x = np.linspace(left_knot - 0.25, right_knot + 0.25, 100)
ax.plot(knot_plot_x, intercept + slope * knot_plot_x,
c=red, lw=2, zorder=100);
ax.set_xlim(-2.1, 2.1);
# In[70]:
fig
# #### Mixture weights
#
# The model has infinitely many mixture components, we truncate to $K$
#
# $$
# \begin{align*}
# \alpha_1, \ldots, \alpha_K
# & \sim N(0, 1) \\
# \beta_1, \ldots, \beta_K
# & \sim N(0, 1) \\
# \boldsymbol{\pi} \ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, x
# & \sim \textrm{Logit-Stick-Breaking}(\boldsymbol{\alpha} + \boldsymbol{\beta} x) \\
# \end{align*}
# $$
# In[71]:
# turn the LIDAR observations into column vectors
# this is important for broadcasting in following
# calculations
std_range = lidar_df.std_range.values[:, np.newaxis]
std_logratio = lidar_df.std_logratio.values[:, np.newaxis]
# The [stick-breaking process](https://en.wikipedia.org/wiki/Dirichlet_process#The_stick-breaking_process) transforms an arbitrary set of values in the interval $[0, 1]$ to a set of weights in $[0, 1]$ that sum to one.
# In[72]:
def stick_breaking(v):
"""
Perform a stick breaking transformation along
the second axis of v
"""
return v * tt.concatenate([tt.ones_like(v[:, :1]),
tt.extra_ops.cumprod(1 - v, axis=1)[:, :-1]],
axis=1)
# In[73]:
K = 20
x_lidar = shared(std_range, broadcastable=(False, True))
with pm.Model() as lidar_model:
alpha = pm.Normal('alpha', 0., 1., shape=K)
beta = pm.Normal('beta', 0., 1., shape=K)
v = tt.nnet.sigmoid(alpha + beta * x_lidar)
pi = pm.Deterministic('pi', stick_breaking(v))
# #### Component linear models
#
# $$
# \begin{align*}
# \gamma_1, \ldots, \gamma_K
# & \sim N(0, 100) \\
# \delta_1, \ldots, \delta_K
# & \sim N(0, 100) \\
# \tau_1, \ldots, \tau_K
# & \sim \textrm{Gamma}(1, 1) \\
# Y_i\ |\ \gamma_i, \delta_i, \tau_i, x
# & \sim N(\gamma_i + \delta_i x, \tau_i^{-1})
# \end{align*}
# $$
# In[74]:
with lidar_model:
gamma = pm.Normal('gamma', 0., 100., shape=K)
delta = pm.Normal('delta', 0., 100., shape=K)
tau = pm.Gamma('tau', 1., 1., shape=K)
ys = pm.Deterministic('ys', gamma + delta * x_lidar)
# #### Observation model
#
# $$
# \begin{align*}
# Y\ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}, \boldsymbol{\delta}, \boldsymbol{\tau}, x
# & = \sum_{i = 1}^K \pi_i Y_i \\
# \end{align*}
# $$
# The `NormalMixture` class is a bit of a hack to marginalize over the categorical indicators that would otherwise be necessary to implement a normal mixture model in PyMC3. This also speeds convergence in both MCMC and variational inference algorithms. See the Stan [_User's Guide and Reference Manual_](http://www.uvm.edu/~bbeckage/Teaching/DataAnalysis/Manuals/stan-reference-2.8.0.pdf) for more information on the benefits of marginalization.
# In[75]:
def normal_mixture_rvs(*args, **kwargs):
w = kwargs['w']
mu = kwargs['mu']
tau = kwargs['tau']
size = kwargs['size']
component = np.array([np.random.choice(w.shape[1], size=size, p=w_ / w_.sum())
for w_ in w])
return sp.stats.norm.rvs(mu[np.arange(w.shape[0]), component], tau[component]**-0.5)
class NormalMixture(pm.distributions.Continuous):
def __init__(self, w, mu, tau, *args, **kwargs):
"""
w is a tesnor of mixture weights
mu is a tensor of the means of the component normal distributions
tau is a tensor of the precisions of the component normal distributions
"""
super(NormalMixture, self).__init__(*args, **kwargs)
self.w = w
self.mu = mu
self.tau = tau
self.mean = (w * mu).sum()
def random(self, point=None, size=None, repeat=None):
"""
Draw a random sample from a normal mixture model
"""
w, mu, tau = draw_values([self.w, self.mu, self.tau], point=point)
return normal_mixture_rvs(w=w, mu=mu, tau=tau, size=size)
def logp(self, value):
"""
The log density of then normal mixture model
"""
w = self.w
mu = self.mu
tau = self.tau
return bound(logsumexp(tt.log(w) + (-tau * (value - mu)**2 + tt.log(tau / np.pi / 2.)) / 2.,
axis=1).sum(),
tau >=0, w >= 0, w <= 1)
# In[76]:
with lidar_model:
lidar_obs = NormalMixture('lidar_obs', pi, ys, tau,
observed=std_logratio)
# #### ADVI inference
# In[77]:
get_ipython().run_cell_magic('time', '', 'N_ADVI_ITER = 50000\n\nwith lidar_model:\n advi_fit = pm.advi(n=N_ADVI_ITER, random_seed=SEED)\n')
# In[78]:
# plot the ELBO over time
fig, ax = plt.subplots()
ax.plot(np.arange(N_ADVI_ITER) + 1, advi_fit.elbo_vals);
ax.set_xlabel('ADVI iteration');
ax.set_ylabel('ELBO');
# In[79]:
fig
# #### Posterior predictions
# In[80]:
PPC_SAMPLES = 5000
lidar_ppc_x = np.linspace(std_range.min() - 0.05,
std_range.max() + 0.05,
100)
with lidar_model:
# sample from the variational posterior distribution
advi_trace = pm.sample_vp(advi_fit, PPC_SAMPLES, random_seed=SEED)
# sample from the posterior predictive distribution
x_lidar.set_value(lidar_ppc_x[:, np.newaxis])
advi_ppc_trace = pm.sample_ppc(advi_trace, PPC_SAMPLES, random_seed=SEED)
# In[81]:
# plot the component mixture weights to assess the impact of truncation
fig, ax = plt.subplots()
ax.bar(np.arange(K) + 1 - 0.4, advi_trace['pi'].mean(axis=0).max(axis=0),
lw=0);
ax.set_xlim(1 - 0.4, K);
ax.set_xlabel('Mixture component');
ax.set_ylabel('Maximum posterior\nexpected mixture weight');
# #### Impact of truncation
# In[82]:
fig
# In[83]:
# plot the posterior predictions for the LIDAR data
fig, ax = plt.subplots()
ax.scatter(lidar_df.std_range, lidar_df.std_logratio,
c=blue, zorder=10);
low, high = np.percentile(advi_ppc_trace['lidar_obs'], [2.5, 97.5], axis=0)
ax.fill_between(lidar_ppc_x, low, high, color='k', alpha=0.35, zorder=5);
ax.plot(lidar_ppc_x, advi_ppc_trace['lidar_obs'].mean(axis=0), c='k', zorder=6);
ax.set_xticklabels([]);
ax.set_xlabel('Range');
ax.set_yticklabels([]);
ax.set_ylabel('Log ratio');
ax.set_title('LIDAR Data');
# In[84]:
fig
# ## References
#
# ### Edward
#
# [edwardlib.org](http://edwardlib.org/)
#
# [Examples](https://github.com/blei-lab/edward/tree/master/examples)
#
# ### PyMC3
#
# [http://pymc-devs.github.io/pymc3/](http://pymc-devs.github.io/pymc3/)
#
# [Examples](http://pymc-devs.github.io/pymc3/examples.html)
#
# PyMC3 port of [_Probabilistic Programming and Bayesian Methods for Hackers_](https://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers#pymc3)
# ### Variational Inference
#
# Angelino, Elaine, Matthew James Johnson, and Ryan P. Adams. "[Patterns of Scalable Bayesian Inference](https://arxiv.org/pdf/1602.05221v2.pdf)." arXiv preprint arXiv:1602.05221 (2016).
#
# Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. "[Variational inference: A review for statisticians](http://arxiv.org/pdf/1601.00670)." arXiv preprint arXiv:1601.00670 (2016).
#
# Kucukelbir, Alp, et al. "[Automatic Differentiation Variational Inference](https://arxiv.org/pdf/1603.00788.pdf)." arXiv preprint arXiv:1603.00788 (2016).
#
# Ranganath, Rajesh, Sean Gerrish, and David M. Blei. "[Black Box Variational Inference]((http://www.cs.columbia.edu/~blei/papers/RanganathGerrishBlei2014.pdf)." AISTATS. 2014.
# ### Models
#
# Bafumi, Joseph, et al. "[Practical issues in implementing and understanding Bayesian ideal point estimation](http://www.stat.columbia.edu/~gelman/research/published/171.pdf)." Political Analysis 13.2 (2005): 171-187.
#
# Fox, Jean-Paul. [_Bayesian item response modeling: Theory and applications_](https://www.amazon.com/Bayesian-Item-Response-Modeling-Applications/dp/1441907416). Springer Science & Business Media, 2010.
#
# Gelman, Andrew, et al. [_Bayesian data analysis_](https://www.amazon.com/Bayesian-Analysis-Chapman-Statistical-Science/dp/B00I60M6H6). Vol. 2. Boca Raton, FL, USA: Chapman & Hall/CRC, 2014.
#
# Gelman, Andrew, and Jennifer Hill. [_Data analysis using regression and multilevel/hierarchical models_](https://www.amazon.com/Analysis-Regression-Multilevel-Hierarchical-Models/dp/052168689X). Cambridge University Press, 2006.
#
# Ren, Lu, et al. "[Logistic stick-breaking process](http://www.jmlr.org/papers/volume12/ren11a/ren11a.pdf)." Journal of Machine Learning Research 12.Jan (2011): 203-239.
# ## Thank You!
#
# ### [@AustinRochford](https://twitter.com/AustinRochford) — [Monetate Labs](http://www.monetate.com/)
#
# ### [arochford@monetate.com](mailto:arochford@monetate.com)
#
#  #
# The [Jupyter](http://jupyter.org/) notebook these slides were generated from is available [here](https://nbviewer.jupyter.org/gist/AustinRochford/91cabfd2e1eecf9049774ce529ba4c16)
# In[85]:
get_ipython().run_cell_magic('bash', '', 'jupyter nbconvert \\\n --to=slides \\\n --reveal-prefix=https://cdnjs.cloudflare.com/ajax/libs/reveal.js/3.2.0/ \\\n --output=variational-python-pydata-dc-2016 \\\n ./PyData\\ DC\\ 2016\\ Variational\\ Inference\\ in\\ Python.ipynb\n')
#
# The [Jupyter](http://jupyter.org/) notebook these slides were generated from is available [here](https://nbviewer.jupyter.org/gist/AustinRochford/91cabfd2e1eecf9049774ce529ba4c16)
# In[85]:
get_ipython().run_cell_magic('bash', '', 'jupyter nbconvert \\\n --to=slides \\\n --reveal-prefix=https://cdnjs.cloudflare.com/ajax/libs/reveal.js/3.2.0/ \\\n --output=variational-python-pydata-dc-2016 \\\n ./PyData\\ DC\\ 2016\\ Variational\\ Inference\\ in\\ Python.ipynb\n')