Algorithmes sur les fonctions¶
Rappel : utilisation des Notebooks¶
Les notebooks, comme celui-ci que vous venez d'ouvrir, sont des pages web interactives dans lesquelles on peut taper du texte courant, du texte mathématiques, ainsi que du code informatique.
Faites une copie du notebook avec la commande ci dessus "File>Make a Copy...", et renommez-le en cliquant sur le titre (à côté de jupyter TD1...), par exemple en rajoutant votre nom.
On peut entrer des expressions (opérations, calculs) ou des instructions (des commandes) dans tous les champs ci-dessous qui commencent par In[..]. Pour taper plusieurs lignes de code à la suite, on appuie sur la touche entrée entre deux lignes (rien de spécial donc).
Le résultat s'obtient avec :
- ctrl + entrée, dans ce cas on reste dans la cellule courante;
- majusucule + entrée, dans ce cas on passe à la cellule suivante.
- Après exécution, le résultat d'un programme est souvent précédé de Out[ ].
Exemple : tapez ctrl entrée après avoir cliqué dans la cellule ci-dessous
En cas de plantage : Si lors d'une tentative d'éxécution de programme, rien ne se passe, c'est probablement que vous avez tapé un programme qui boucle infiniment. Dans ce cas, commencez par sauver votre travail. Puis deux possibilités:
- essayez d'abord de redémarrer le noyau Python (restart dans le menu kernel en haut de la page)
- sinon, allez dans l'onglet "Home", et fermez le TD : cocher la case correspondante, "shutdown" en haut de la page. Fermez ensuite l'onglet du TD, et relancez-le à partir de "Home".
Si vous voulez reprendre ce TD chez vous, le plus simple est d'installer le navigateur Anaconda (puis cliquer sur launch jupyter notebook etc.).
Méthode des rectangles pour le calcul d'une intégrale¶
Soit $f$ une fonction positive et continue sur [$a$ ; $b$]. On a vu en cours un algorithme qui permet de calculer une valeur approchée de l'intégrale de la fonction $f$ sur l'intervalle [$a$ ; $b$].
Algortihme¶
Algorithme en langage "naturel":
Algorithme : méthode des rectangles
entrée : une fonction $f$ intégrable sur un intervalle [$a$ ; $b$].
entrée : les réels $a$ et $b$.
entrée : un entier naturel strictement positif $n$ donnant le nombre de rectangles
sortie : une valeur approchée de l'intégrale $\displaystyle \int_{a}^{b} f(x) \, \mathrm{d}x$
Début
Rentrer $a$
Rentrer $b$ Donner $f$
$pas$ $\leftarrow \frac{b-a}{n}$
$x \leftarrow a$
$somme \leftarrow 0$
Pour i de 1 à n faire:$somme \leftarrow somme + pas\times f(x)$
$x \leftarrow x + pas$
Fin pour
afficher $somme$
Fin
Exercice 1¶
Le programme Python ci-dessous est à compléter pour implémenterc et algorithme. Par rapport aux programmes précédents, vous remarquerez que sa structure est différente.
Il comporte quatre parties, dont deux que vous ne modifierez pas (sous peine de probable plantage !):
- une fonction d'affichage de la fonction $f$ et des rectangles (ne pas y toucher)
- une fonction définissant la fonction $f$, que vous pouvez modifier pour mettre une autre fonction
- une fonction de calcul de la somme des aires des rectangles, à compléter suivant l'algorihtme ci-dessus.
- le programme principal, à ne pas modifier, qui coordonne l'appel des trois fonctions précédentes.
Rappelez-vous de la syntaxe en Python : il y a deux points après un "for", et on indente. Et les virgules des nombres sont des points...
# -*- coding: utf-8 -*-
"""
Frédéric Mandon
"""
# Ne pas modifier les trois lignes ci-dessous
from math import *
import matplotlib.pyplot as plt
import numpy as np
def f(x):
"""
Fonction f(x) = x^2, a modifier si on veut une autre fonction
@param : x un réel pour lequel f est definie
@return : y réel, image de x par f
"""
y = x**2
return y
def rectangles1(f,a,b, n):
"""
Premiere version de l'algorithme des rectangles pour le calcul approche d'une integrale
@param : f fonction dont on veut calculer l'integrale
@param : a reel borne inferieure de l'integrale
@param : b reel borne superieure de l'integrale
@param : n entier nombre de rectangles
@return : somme valeur approchee de 'lintegrale de f entre a et b
Remarque: la partie graphique ne peut fonctionner que si l'on conserve les memes
notation pour les variables que dans l'algorithme, c'est a dire x et pas.
"""
# Completer
for i : # a completer
# mettre le code avant la partie graphique
# fin du code
# Ci-dessous pour tracer un segment [AB] ou A(xA,yA) et B(xB,YB), on ecrit d'abort [xA,xB] puis [yA,Yb]
plt.plot([x-pas,x-pas],[0,f(x-pas)],linewidth=1.0,linestyle ="-",color="red") #segment vertical gauche
plt.plot([x,x],[0,f(x)],linewidth=1.0,linestyle ="-",color="red") #segment vertical droit
plt.plot([x-pas,x],[f(x-pas),f(x-pas)],linewidth=1.0,linestyle ="-",color="red") #segment horizontal
"""
Pour l'exercice 2, remplacer les trois lignes précédentes par
plt.plot([x-pas,x-pas],[0,f(x)],linewidth=1.0,linestyle ="-",color="red") #segment vertical gauche
plt.plot([x,x],[0,f(x)],linewidth=1.0,linestyle ="-",color="red") #segment vertical droit
plt.plot([x-pas,x],[f(x),f(x)],linewidth=1.0,linestyle ="-",color="red") #segment horizontal
"""
return somme
################
#
# PROGRAMME PRINCIPAL ET PARTIE GRAPHIQUE
#
################
# Quelques lignes a modifier eventuellement dans la partie graphique
a = int(input("Donner la valeur de a :"))
b = int(input("Donner la valeur de b :"))
n = int(input("Donner le nombre d'intervalles : "))
# Creation d'une nouvelle figure taille 8x6, resolution 80 points par pouce
plt.figure(figsize=(8,8), dpi=80)
# Tracé de la courbe
debut = a
fin = b
X = np.linspace(debut, fin, 50*(b-a),endpoint=True)
######################################################
# ECRIRE CI-DESSOUS Y=f(X) AVEC X ET Y EN MAJUSCULES #
# en detaillant f exactement comme dans la fonction #
# def f(x) co dessus #
######################################################
Y = X**2
plt.plot(X, Y, label = "Rectangles")
plt.legend(loc = 2)
# placement des axes
ax = plt.gca()
ax.spines['right'].set_color('none') # aucune couleur aux axes a droite et en
ax.spines['top'].set_color('none') # haut => ils disparaissent
ax.spines['bottom'].set_position(('data',0)) # centrage des axes
somme = rectangles1(f,a,b,n) # appel de la fonction rectangles
texte = "Une valeur approchée de l'intégrale est : "+str(somme)+" unités d'aires"
# ecriture du resultat sur le dessin et dans le shell
ax.text(a + 0.05, 0.3, texte, style='italic', bbox={'facecolor':'#4EECDF', 'alpha':1, 'pad':10})
print(texte)
plt.show()
Exercice 2¶
Modifier l'algorihtme précédent pour calculer la somme des aires des rectangles de côté [$x_i$ ; $x_{i + 1}$] avec comme hauteur $f(x_{i + 1})$.
Vous avez le code dans le programme précédent, pour modifier le schéma de manière à ce qu'il corresponde au calcul.
Exercice 3¶
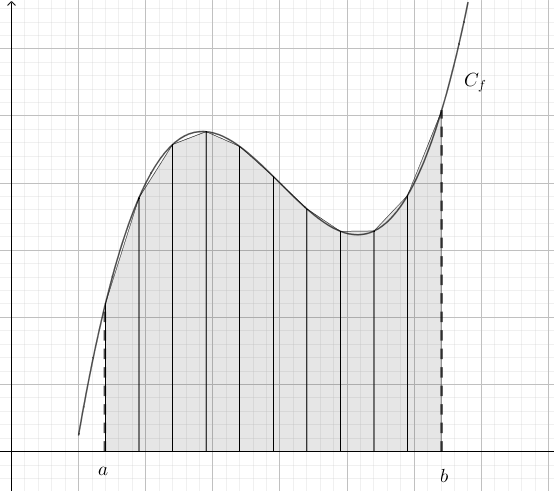
Modifier l'algorithme précédent pour calculer la somme des aires des trapèzes, comme ci-dessous, et non plus des rectangles.
Vous pouvez également modifier le code pour avoir un schéma correct.
Dichotomie¶
L'algorithme de dichotomie permet de calculer la valeur approchée de la solution d'une équation $f(x) = 0$.
Soit $f$ une fonction continue sur un intervalle [$a$ ; $b$], telle que $f(a)$ et $f(b)$ soient de signe opposés. Alors, d'après le théorème des valeurs intermédiaires, l'équation $f(x) = 0$ admet (au moins) une solution sur [$a$ ; $b$]. Pur plus de commodité, on considèrera une fonction n'ayant qu'une racine sur [$a$ ; $b$].
Le principe de la dichotomie consiste à diviser en deux l'intervalle à chaque itération, en choisissant le sous-intervalle contenant la racine de $f$.
Algorithme¶
Algorithme en langage "naturel", à bien comprendre
Algorithme : calcul d'une racine
entrée : une fonction $f$ continue sur un intervalle [$a$ ; $b$], telle que l'équation $f(x) = 0$ n'admette qu'une solution sur cet intervalle.
entrée : les réels $a$ et $b$.
entrée : $\epsilon$ (epsilon), la précision attendue sur la racine
sortie : une valeur approchée de la solution de l'équation $f(x) = 0$
Début
Rentrer $a$
Rentrer $b$
Donner $\epsilon$
Tant que $|b - a| > \epsilon$ :$m \leftarrow \frac{a + b}{2}$
si $f(a)\times f(b) > 0$$a \leftarrow m$
sinon
$b \leftarrow m$
Fin tant que
afficher $a$
Fin
Exercice 1¶
Faire tourner l'algorithme à la main, en donnant le tableau des valeurs $a$, $b$ et $m$, à chaque itération, pour résoudre l'équation $x^3 - 3x^2 + 1 = 0$ à $10^{-1}$ près
Exercice 2¶
- Compléter le programme Python suivant pour implémenter l'algorithme de dichotomie (remarque : on tape
1e-10pour avoir une précision de $10^{-10}$ par exemple). - Le deuxième schéma donne l'erreur en fonction des itérations. L'erreur diminue-t-elle à chaque étape ? Pouvez expliquer le phénomène (c'est une question rhétorique, vous pouvez l'expliquer, donc faites-le).
- Tester l'algortihme avec les fonctions en commentaire, l'une des deux peut donner des résultats surprenants.
# -*- coding: utf-8 -*-
"""
Frédéric Mandon
"""
# Ne pas modifier les trois lignes ci-dessous
from math import *
import matplotlib.pyplot as plt
import numpy as np
def f(x):
"""
Fonction f(x) = x^3 - 3x^2 + 1
@param : x un réel pour lequel f est definie
@return : y réel, image de x par f
"""
#y = float(0.125*x*(63*x**4-70*x*x+15))
# y = x*exp(x) -3
y = x**3 -3*x**2 +1
return y
def dichotomie(f,a,b, epsilon):
"""
Calcul d'une racine d'une fonction
@param : f fonction dont on veut trouver une racine
@param : a reel borne inferieure de l'intervalle
@param : b reel borne superieure de l'intervalle
@param : epsilon reel precision demandee
@return : m valeur approchee de la solution de f(x) = 0
@return : i,valeurs variables pour l'affichage des erreurs
Remarque: la partie graphique ne peut fonctionner que si l'on conserve les memes
notation pour les variables que dans l'algorithme, c'est a dire m, a et b.
"""
# ne pas modifier les lignes deja tapees, sauf le while a completer
i=1
valeurs = []
while :
# code a completer ci-dessous
# fin du code a completer
valeurs.append(m)
i = i + 1
plt.plot([m, m], [0, f(m)],linewidth=1.0,linestyle ="-",color="red",marker = "x")
return m,i,valeurs
a = float(input("borne inférieure de départ : ")) # on rentre les bornes
b = float(input("borne supérieure de départ : "))
eps = float(input("précision demandée : "))
# Creation d'une nouvelle figure taille 8x6, resolution 80 points par pouce
plt.figure(figsize=(8,12), dpi=80)
# Tracé de la courbe
debut = a
fin = b
plt.subplot(2,1,1)
X = np.linspace(debut, fin, int(50*(b-a)),endpoint=True)
######################################################
# ECRIRE CI-DESSOUS Y=f(X) AVEC X ET Y EN MAJUSCULES #
# en detaillant f exactement comme dans la fonction #
# def f(x) co dessus #
######################################################
Y = (X**3 -3*X**2 +1)
plt.plot(X, Y)
plt.title("Dichotomie", {'fontsize': 'large', 'fontweight' :'bold'} )
# placement des axes
ax = plt.gca()
ax.spines['right'].set_color('none') # aucune couleur aux axes a droite et en
ax.spines['top'].set_color('none') # haut => ils disparaissent
ax.spines['bottom'].set_position(('data',0)) # centrage des axes
rac,iter,valeurs = dichotomie(f,a,b,eps)
texte = "Une valeur approchée de la racine est : "+str(rac)
# ecriture du resultat sur le dessin et dans le shell
ax.text(a + 0.05, f(a + 0.05), texte, style='italic', bbox={'facecolor':'#4EECDF', 'alpha':1, 'pad':10})
print(rac)
print(iter-1)
print(len(valeurs))
erreur_abs = []
for i in range(len(valeurs)):
erreur_abs.append(abs(valeurs[i]-valeurs[len(valeurs)-1]))
print(erreur_abs)
print(valeurs)
print(i)
# Tracé de l'erreur en focntion du nombre d'itérations
plt.subplot(2,1,2)
X = list(range(len(valeurs)))
plt.yscale('log')
plt.plot(X,erreur_abs,label = "erreur Dicho")
plt.legend()
plt.show()