Examples on scalar differential equations (ODEs)¶
Terminology:
Scalar ODE: a single ODE, one unknown function
Vector ODE or systems of ODEs: several ODEs, several unknown functions
Examples:
We shall write an ODE in a generic form: $u'=f(u,t)$¶
Our methods and software should be applicable to any ODE
Therefore we need an abstract notation for an arbitrary ODE
The three ODEs on the last slide correspond to
Our task: write functions and classes that take $f$ as input and produce $u$ as output
What is the $f(u,t)$?¶
Problem:
Given an ODE,
what is the $f(u,t)$?
Solution:
The target form is $u'=f(u,t)$, so we need to isolate $u'$ on the left-hand side:
Such abstract $f$ functions are widely used in mathematics¶
We can make generic software for:
Numerical differentiation: $f'(x)$
Numerical integration: $\int_a^b f(x)dx$
Numerical solution of algebraic equations: $f(x)=0$
Applications:
$\frac{d}{dx} x^a\sin (wx)$: $f(x)=x^a\sin (wx)$
$\int_{-1}^1 (x^2\tanh^{-1}x - (1+x^2)^{-1})dx$: $f(x)=x^2\tanh^{-1}x - (1+x^2)^{-1}$, $a=-1$, $b=1$
Solve $x^4\sin x = \tan x$: $f(x)=x^4\sin x - \tan x$
We use finite difference approximations to derivatives to turn an ODE into a difference equation¶
$u'=f(u,t)$.
Assume we have computed $u$ at discrete time points $t_0,t_1,\ldots,t_k$. At $t_k$ we have the ODE
Approximate $u'(t_k)$ by a forward finite difference,
Insert in the ODE at $t=t_k$:
This is a very simple formula that we can use repeatedly for $u(t_1)$, $u(t_2)$, $u(t_3)$ and so forth.
Difference equation notation:
Let $u_k$ denote the numerical approximation to the exact solution $u(t)$ at $t=t_k$.
Solve for $u$ at $t=t_k=k\Delta t$, $k=0,1,2,\ldots,t_n$, $t_0=0$, $t_n=T$
Forward Euler method:
Solution by hand:
What is $f$? $f(u,t)=u$
First step:
but what is $u_0$?
An ODE needs an initial condition: $u(0)=U_0$¶
Numerics:
Any ODE $u'=f(u,t)$ must have an initial condition $u(0)=U_0$, with known $U_0$, otherwise we cannot start the method!
Mathematics:
In mathematics: $u(0)=U_0$ must be specified to get a unique solution.
Example:
Solution: $u=Ce^t$ for any constant $C$. Say $u(0)=U_0$: $u=U_0e^t$.
We continue solution by hand¶
Say $U_0=2$:
Actually, we found a formula for $u_k$! No need to program...
How accurate is our numerical method?¶
Exact solution: $u(t)=2e^t$, $u(t_k)=2e^{k\Delta t} = 2(e^{\Delta t})^k$
Numerical solution: $u_k = 2(1+\Delta t)^k$
When going from $t_k$ to $t_{k+1}$, the solution is amplified by a factor:
Exact: $u(t_{k+1}) = e^{\Delta t}u(t_k)$
Numerical: $u_{k+1} = (1+\Delta t)u_k$
Using Taylor series for $e^x$ we see that
This error approaches 0 as $\Delta t\rightarrow 0$.
What about the general case $u'=f(u,t)$?¶
Given any $U_0$:
No general formula in this case...
Rule of thumb:
When hand calculations get boring, let's program!
We start with a specialized program for $u'=u$, $u(0)=U_0$¶
Algorithm:
Given $\Delta t$ (dt) and $n$
Create arrays
tanduof length $n+1$Set initial condition:
u[0]= $U_0$,t[0]=0For $k=0,1,2,\ldots,n-1$:
t[k+1] = t[k] + dtu[k+1] = (1 + dt)*u[k]
We start with a specialized program for $u'=u$, $u(0)=U_0$¶
Program:
import numpy as np
import sys
dt = float(sys.argv[1])
U0 = 1
T = 4
n = int(T/dt)
t = np.zeros(n+1)
u = np.zeros(n+1)
t[0] = 0
u[0] = U0
for k in range(n):
t[k+1] = t[k] + dt
u[k+1] = (1 + dt)*u[k]
# plot u against t
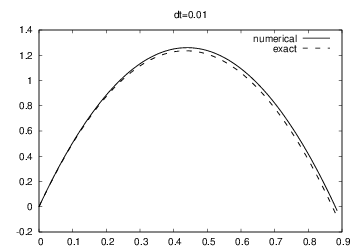
The solution if we plot $u$ against $t$¶
$\Delta t = 0.4$ and $\Delta t=0.2$:
The algorithm for the general ODE $u'=f(u,t)$¶
Algorithm:
Given $\Delta t$ (dt) and $n$
Create arrays
tanduof length $n+1$Create array
uto hold $u_k$ andSet initial condition:
u[0]= $U_0$,t[0]=0For $k=0,1,2,\ldots,n-1$:
u[k+1] = u[k] + dt*f(u[k], t[k])(the only change!)t[k+1] = t[k] + dt
Implementation of the general algorithm for $u'=f(u,t)$¶
General function:
def ForwardEuler(f, U0, T, n):
"""Solve u'=f(u,t), u(0)=U0, with n steps until t=T."""
import numpy as np
t = np.zeros(n+1)
u = np.zeros(n+1) # u[k] is the solution at time t[k]
u[0] = U0
t[0] = 0
dt = T/float(n)
for k in range(n):
t[k+1] = t[k] + dt
u[k+1] = u[k] + dt*f(u[k], t[k])
return u, t
Magic:
This simple function can solve any ODE (!)
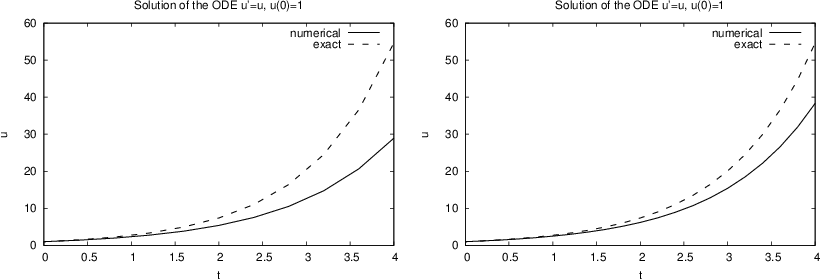
Example on using the function¶
Mathematical problem:
Solve $u'=u$, $u(0)=1$, for $t\in [0,4]$, with $\Delta t = 0.4$ Exact solution: $u(t)=e^t$.
Basic code:
def f(u, t):
return u
U0 = 1
T = 3
n = 30
u, t = ForwardEuler(f, U0, T, n)
Compare exact and numerical solution:
%matplotlib inline
from scitools.std import plot, exp
u_exact = exp(t)
plot(t, u, 'r-', t, u_exact, 'b-',
xlabel='t', ylabel='u', legend=('numerical', 'exact'),
title="Solution of the ODE u'=u, u(0)=1")
Now you can solve any ODE!¶
Recipe:
Identify $f(u,t)$ in your ODE
Make sure you have an initial condition $U_0$
Implement the $f(u,t)$ formula in a Python function
f(u, t)Choose $\Delta t$ or no of steps $n$
Call
u, t = ForwardEuler(f, U0, T, n)plot(t, u)
Warning:
The Forward Euler method may give very inaccurate solutions if $\Delta t$ is not sufficiently small. For some problems (like $u''+u=0$) other methods should be used.
Let us make a class instead of a function for solving ODEs¶
Usage of the class:
method = ForwardEuler(f, dt)
method.set_initial_condition(U0, t0)
u, t = method.solve(T)
plot(t, u)
How?
Store $f$, $\Delta t$, and the sequences $u_k$, $t_k$ as attributes
Split the steps in the
ForwardEulerfunction into four methods:the constructor (
__init__)set_initial_conditionfor $u(0)=U_0$solvefor running the numerical time steppingadvancefor isolating the numerical updating formula (new numerical methods just need a differentadvancemethod, the rest is the same)
The code for a class for solving ODEs (part 1)¶
import numpy as np
class ForwardEuler_v1:
def __init__(self, f, dt):
self.f, self.dt = f, dt
def set_initial_condition(self, U0):
self.U0 = float(U0)
The code for a class for solving ODEs (part 2)¶
class ForwardEuler_v1:
...
def solve(self, T):
"""Compute solution for 0 <= t <= T."""
n = int(round(T/self.dt)) # no of intervals
self.u = np.zeros(n+1)
self.t = np.zeros(n+1)
self.u[0] = float(self.U0)
self.t[0] = float(0)
for k in range(self.n):
self.k = k
self.t[k+1] = self.t[k] + self.dt
self.u[k+1] = self.advance()
return self.u, self.t
def advance(self):
"""Advance the solution one time step."""
# Create local variables to get rid of "self." in
# the numerical formula
u, dt, f, k, t = self.u, self.dt, self.f, self.k, self.t
unew = u[k] + dt*f(u[k], t[k])
return unew
Alternative class code for solving ODEs (part 1)¶
# Idea: drop dt in the constructor.
# Let the user provide all time points (in solve).
class ForwardEuler:
def __init__(self, f):
# test that f is a function
if not callable(f):
raise TypeError('f is %s, not a function' % type(f))
self.f = f
def set_initial_condition(self, U0):
self.U0 = float(U0)
def solve(self, time_points):
...
Alternative class code for solving ODEs (part 2)¶
class ForwardEuler:
...
def solve(self, time_points):
"""Compute u for t values in time_points list."""
self.t = np.asarray(time_points)
self.u = np.zeros(len(time_points))
self.u[0] = self.U0
for k in range(len(self.t)-1):
self.k = k
self.u[k+1] = self.advance()
return self.u, self.t
def advance(self):
"""Advance the solution one time step."""
u, f, k, t = self.u, self.f, self.k, self.t
dt = t[k+1] - t[k]
unew = u[k] + dt*f(u[k], t[k])
return unew
Verifying the class implementation; mathematics¶
Mathematical problem:
Important result: the numerical method (and most others) will exactly reproduce $u$ if it is linear in $t$ (!):
This $u$ should be reproduced to machine precision for any $\Delta t$.
Verifying the class implementation; implementation¶
Code:
def test_ForwardEuler_against_linear_solution():
def f(u, t):
return 0.2 + (u - h(t))**4
def h(t):
return 0.2*t + 3
solver = ForwardEuler(f)
solver.set_initial_condition(U0=3)
dt = 0.4; T = 3; n = int(round(float(T)/dt))
time_points = np.linspace(0, T, n+1)
u, t = solver.solve(time_points)
u_exact = h(t)
diff = np.abs(u_exact - u).max()
tol = 1E-14
success = diff < tol
assert success
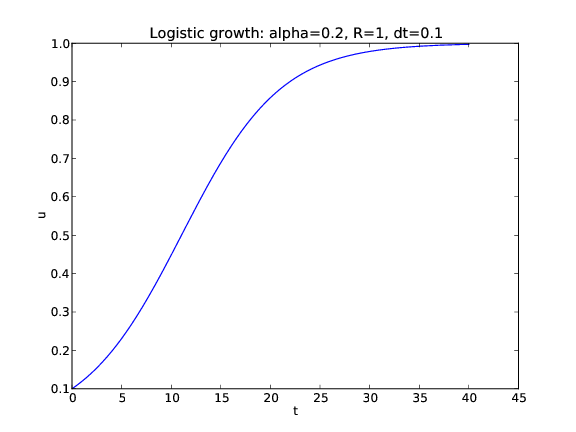
Using a class to hold the right-hand side $f(u,t)$¶
Mathematical problem:
Class for right-hand side $f(u,t)$:
class Logistic:
def __init__(self, alpha, R, U0):
self.alpha, self.R, self.U0 = alpha, float(R), U0
def __call__(self, u, t): # f(u,t)
return self.alpha*u*(1 - u/self.R)
Main program:
problem = Logistic(0.2, 1, 0.1)
time_points = np.linspace(0, 40, 401)
method = ForwardEuler(problem)
method.set_initial_condition(problem.U0)
u, t = method.solve(time_points)
4th-order Runge-Kutta method:
And lots of other methods! How to program a wide collection of methods? Use object-oriented programming!
A superclass for ODE methods¶
Common tasks for ODE solvers:
Store the solution $u_k$ and the corresponding time levels $t_k$, $k=0,1,2,\ldots,n$
Store the right-hand side function $f(u,t)$
Set and store the initial condition
Run the loop over all time steps
Principles:
Common data and functionality are placed in superclass
ODESolverIsolate the numerical updating formula in a method
advanceSubclasses, e.g.,
ForwardEuler, just implement the specific numerical formula inadvance
The superclass code¶
class ODESolver:
def __init__(self, f):
self.f = f
def advance(self):
"""Advance solution one time step."""
raise NotImplementedError # implement in subclass
def set_initial_condition(self, U0):
self.U0 = float(U0)
def solve(self, time_points):
self.t = np.asarray(time_points)
self.u = np.zeros(len(self.t))
# Assume that self.t[0] corresponds to self.U0
self.u[0] = self.U0
# Time loop
for k in range(n-1):
self.k = k
self.u[k+1] = self.advance()
return self.u, self.t
def advance(self):
raise NotImplemtedError # to be impl. in subclasses
Implementation of the Forward Euler method¶
Subclass code:
class ForwardEuler(ODESolver):
def advance(self):
u, f, k, t = self.u, self.f, self.k, self.t
dt = t[k+1] - t[k]
unew = u[k] + dt*f(u[k], t)
return unew
Application code for $u'-u=0$, $u(0)=1$, $t\in [0,3]$, $\Delta t=0.1$:
from ODESolver import ForwardEuler
def test1(u, t):
return u
method = ForwardEuler(test1)
method.set_initial_condition(U0=1)
u, t = method.solve(time_points=np.linspace(0, 3, 31))
plot(t, u)
The implementation of a Runge-Kutta method¶
Subclass code:
class RungeKutta4(ODESolver):
def advance(self):
u, f, k, t = self.u, self.f, self.k, self.t
dt = t[k+1] - t[k]
dt2 = dt/2.0
K1 = dt*f(u[k], t)
K2 = dt*f(u[k] + 0.5*K1, t + dt2)
K3 = dt*f(u[k] + 0.5*K2, t + dt2)
K4 = dt*f(u[k] + K3, t + dt)
unew = u[k] + (1/6.0)*(K1 + 2*K2 + 2*K3 + K4)
return unew
Application code (same as for ForwardEuler):
from ODESolver import RungeKutta4
def test1(u, t):
return u
method = RungeKutta4(test1)
method.set_initial_condition(U0=1)
u, t = method.solve(time_points=np.linspace(0, 3, 31))
plot(t, u)
The user should be able to check intermediate solutions and terminate the time stepping¶
Sometimes a property of the solution determines when to stop the solution process: e.g., when $u < 10^{-7}\approx 0$.
Extension:
solve(time_points, terminate)terminate(u, t, step_no)is called at every time step, is user-defined, and returnsTruewhen the time stepping should be terminatedLast computed solution is
u[step_no]at timet[step_no]
def terminate(u, t, step_no):
eps = 1.0E-6 # small number
return abs(u[step_no,0]) < eps # close enough to zero?
Systems of differential equations (vector ODE)¶
Each unknown must have an initial condition, say
In this case, one can derive the exact solution to be
Systems of ODEs appear frequently in physics, biology, finance, ...
The ODE system that is the final project in the course¶
Model for spreading of a disease in a population:
Initial conditions:
Another example on a system of ODEs (vector ODE)¶
Second-order ordinary differential equation, for a spring-mass system (from Newton's second law):
We can rewrite this as a system of two first-order equations, by introducing two new unknowns
The first-order system is then
Initial conditions: $u^{(0)}(0) = U_0$, $u^{(1)}(0)=0$
Making a flexible toolbox for solving ODEs¶
For scalar ODEs we could make one general class hierarchy to solve "all" problems with a range of methods
Can we easily extend class hierarchy to systems of ODEs?
Yes!
The example here can easily be extended to professional code (Odespy)
Vector notation for systems of ODEs: unknowns and equations¶
General software for any vector/scalar ODE demands a general mathematical notation. We introduce $n$ unknowns
in a system of $n$ ODEs:
Vector notation for systems of ODEs: vectors¶
We can collect the $u^{(i)}(t)$ functions and right-hand side functions $f^{(i)}$ in vectors:
The first-order system can then be written
where $u$ and $f$ are vectors and $U_0$ is a vector of initial conditions
The magic of this notation:
Observe that the notation makes a scalar ODE and a system look the same, and we can easily make Python code that can handle both cases within the same lines of code (!)
How to make class ODESolver work for systems of ODEs¶
Recall: ODESolver was written for a scalar ODE
Now we want it to work for a system $u'=f$, $u(0)=U_0$, where $u$, $f$ and $U_0$ are vectors (arrays)
What are the problems?
Forward Euler applied to a system:
In Python code:
unew = u[k] + dt*f(u[k], t)
where
uis a two-dim. array (u[k]is a row)fis a function returning an array (all the right-hand sides $f^{(0)},\ldots,f^{(n-1)}$)
The adjusted superclass code (part 1)¶
To make ODESolver work for systems:
Ensure that
f(u,t)returns an array. This can be done be a general adjustment in the superclass!Inspect $U_0$ to see if it is a number or list/tuple and make corresponding
u1-dim or 2-dim array
class ODESolver:
def __init__(self, f):
# Wrap user's f in a new function that always
# converts list/tuple to array (or let array be array)
self.f = lambda u, t: np.asarray(f(u, t), float)
def set_initial_condition(self, U0):
if isinstance(U0, (float,int)): # scalar ODE
self.neq = 1 # no of equations
U0 = float(U0)
else: # system of ODEs
U0 = np.asarray(U0)
self.neq = U0.size # no of equations
self.U0 = U0
The superclass code (part 2)¶
class ODESolver:
...
def solve(self, time_points, terminate=None):
if terminate is None:
terminate = lambda u, t, step_no: False
self.t = np.asarray(time_points)
n = self.t.size
if self.neq == 1: # scalar ODEs
self.u = np.zeros(n)
else: # systems of ODEs
self.u = np.zeros((n,self.neq))
# Assume that self.t[0] corresponds to self.U0
self.u[0] = self.U0
# Time loop
for k in range(n-1):
self.k = k
self.u[k+1] = self.advance()
if terminate(self.u, self.t, self.k+1):
break # terminate loop over k
return self.u[:k+2], self.t[:k+2]
All subclasses from the scalar ODE works for systems as well
Example on how to use the general class hierarchy¶
Spring-mass system formulated as a system of ODEs:
Code defining the right-hand side:
def myf(u, t):
# u is array with two components u[0] and u[1]:
return [u[1],
-beta*u[1]/m - k*u[0]/m]
Alternative implementation of the $f$ function via a class¶
Better (no global variables):
class MyF:
def __init__(self, m, k, beta):
self.m, self.k, self.beta = m, k, beta
def __call__(self, u, t):
m, k, beta = self.m, self.k, self.beta
return [u[1], -beta*u[1]/m - k*u[0]/m]
Main program:
from ODESolver import ForwardEuler
# initial condition:
U0 = [1.0, 0]
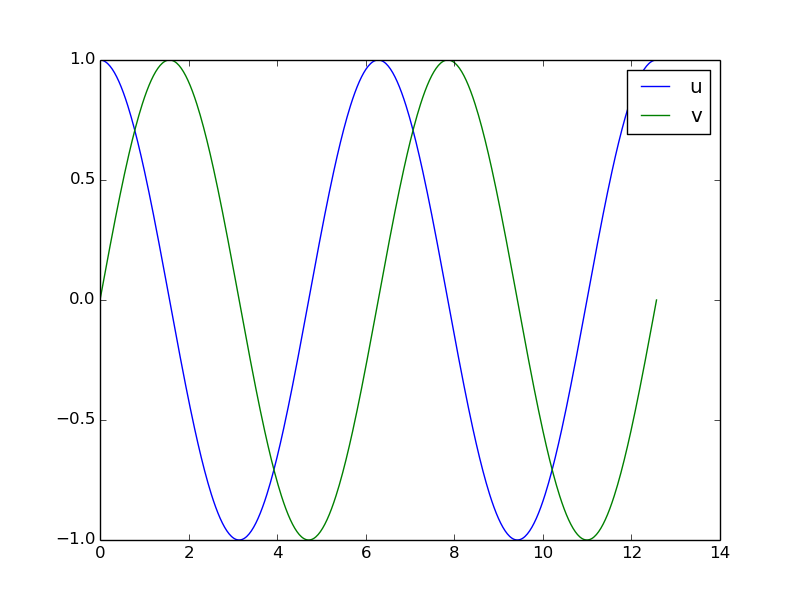
f = MyF(1.0, 1.0, 0.0) # u'' + u = 0 => u(t)=cos(t)
solver = ForwardEuler(f)
solver.set_initial_condition(U0)
T = 4*pi; dt = pi/20; n = int(round(T/dt))
time_points = np.linspace(0, T, n+1)
u, t = solver.solve(time_points)
# u is an array of [u0,u1] arrays, plot all u0 values:
u0_values = u[:,0]
u0_exact = cos(t)
plot(t, u0_values, 'r-', t, u0_exact, 'b-')
Throwing a ball; ODE model¶
Newton's 2nd law for a ball's trajectory through air leads to
Air resistance is neglected but can easily be added!
4 ODEs with 4 unknowns:
the ball's position $x(t)$, $y(t)$
the velocity $v_x(t)$, $v_y(t)$
Throwing a ball; code¶
Define the right-hand side:
def f(u, t):
x, vx, y, vy = u
g = 9.81
return [vx, 0, vy, -g]
Main program:
from ODESolver import ForwardEuler
# t=0: prescribe x, y, vx, vy
x = y = 0 # start at the origin
v0 = 5; theta = 80*pi/180 # velocity magnitude and angle
vx = v0*cos(theta)
vy = v0*sin(theta)
# Initial condition:
U0 = [x, vx, y, vy]
solver= ForwardEuler(f)
solver.set_initial_condition(u0)
time_points = np.linspace(0, 1.2, 101)
u, t = solver.solve(time_points)
# u is an array of [x,vx,y,vy] arrays, plot y vs x:
x = u[:,0]; y = u[:,2]
plot(x, y)
$R$ is the maximum population size, which can vary with changes in the environment over time
Implementation features:
Class Problem holds "all physics": $\alpha$, $R(t)$, $U_0$, $T$ (end time), $f(u,t)$ in ODE
Class Solver holds "all numerics": $\Delta t$, solution method; solves the problem and plots the solution
Solve for $t\in [0,T]$ but terminate when $|u-R| < \hbox{tol}$
Logistic growth model; class Problem ($f$)¶
class Problem:
def __init__(self, alpha, R, U0, T):
self.alpha, self.R, self.U0, self.T = alpha, R, U0, T
def __call__(self, u, t):
"""Return f(u, t)."""
return self.alpha*u*(1 - u/self.R(t))
def terminate(self, u, t, step_no):
"""Terminate when u is close to R."""
tol = self.R*0.01
return abs(u[step_no] - self.R) < tol
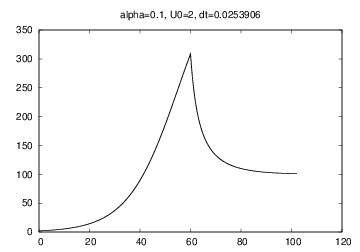
problem = Problem(alpha=0.1, R=500, U0=2, T=130)
Logistic growth model; class Solver¶
class Solver:
def __init__(self, problem, dt,
method=ODESolver.ForwardEuler):
self.problem, self.dt = problem, dt
self.method = method
def solve(self):
solver = self.method(self.problem)
solver.set_initial_condition(self.problem.U0)
n = int(round(self.problem.T/self.dt))
t_points = np.linspace(0, self.problem.T, n+1)
self.u, self.t = solver.solve(t_points,
self.problem.terminate)
def plot(self):
plot(self.t, self.u)
problem = Problem(alpha=0.1, U0=2, T=130,
R=lambda t: 500 if t < 60 else 100)
solver = Solver(problem, dt=1.)
solver.solve()
solver.plot()
print 'max u:', solver.u.max()
Logistic growth model; results¶