v0 = 5
g = 9.81
t = 0.6
y = v0*t - 0.5*g*t**2
print y
Note:
Input data ($v_0$, $t$) are hardcoded (explicitly set)
Changing input data requires editing
This is considered bad programming (because editing programs may easily introduce errors!)
Rule: read input from user - avoid editing a correct program
How do professional programs get their input?¶
Consider a web browser: how do you specify a web address? How do you change the font?
You don't need to go into the program and edit it...
How can we specify input data in programs?¶
Hardcode values
Ask the user questions and read answers
Read command-line arguments
Read data from a file
Getting input from questions and anwsers¶
Sample program:
C = 21; F = (9.0/5)*C + 32; print F
Idea: let the program ask the user a question "C=?", read the user's answer, assign that answer to the variable C.
C = raw_input('C=? ') # C becomes a string
C = float(C) # convert to float so we can compute
F = (9./5)*C + 32
print F
Another example: print the n first even numbers¶
n = int(raw_input('n=? '))
for i in range(2, 2*n+1, 2):
print i
# or:
print range(2, 2*n+1, 2)
# or:
for i in range(1, n+1):
print 2*i
Command-line arguments are words written after the program name¶
Examples on command-line arguments:
Terminal> python myprog.py arg1 arg2 arg3 ...
Terminal> cp -r yourdir ../mydir
Terminal> ls -l
Unix programs (rm, ls, cp, ...) make heavy use of command-line arguments, (see e.g. man ls). We shall do the same.
How to use a command-line argument in our sample program¶
C = 21; F = (9.0/5)*C + 32; print F
The user wants to specify C as a command-line argument
after the name of the program when we run the program:
Terminal> python c2f_cml.py 21
69.8
Command-line arguments are the "words" after the program name,
and they are stored in the list sys.argv:
# Need to fill in sys.argv for use in the notebook
import sys
sys.argv[1] = '21'
Below is the ordinary program:
import sys
C = float(sys.argv[1]) # read 1st command-line argument
F = 9.0*C/5 + 32
print F
Command-line arguments are separated by blanks¶
Here is another program print_cml.py:
import sys; print sys.argv[1:]
Demonstrations:
Terminal> python print_cml.py 21 string with blanks 1.3
['21', 'string', 'with', 'blanks', '1.3']
Terminal> python print_cml.py 21 "string with blanks" 1.3
['21', 'string with blanks', '1.3']
Note 1: use quotes, as in "string with blanks", to override the rule
that command-line arguments are separate by blanks.
Note 2: all list elements are surrounded by quotes, demonstrating that command-line arguments are strings.
The magic eval function turns a string into live code¶
eval(s) evaluates a string object s as if the string had been
written directly into the program
s = '1+2'
r = eval(s)
r
type(r)
r = eval('[1, 6, 7.5] + [1, 2]')
r
type(r)
Note: be careful with eval and string values¶
We want r = 'math programming'. Writing just
r = eval('math programming')
is the same as writing
r = math programming
which is an invalid expression and illegal syntax.
Remedy: must put the string inside quotes:
s = "'math programming'"
r = eval(s)
r
With eval, a little program (add_input.py) can do much...¶
Program:
i1 = eval(raw_input('Give input: '))
i2 = eval(raw_input('Give input: '))
r = i1 + i2
print '%s + %s becomes %s\nwith value %s' % \
(type(i1), type(i2), type(r), r)
We can add integer and float:
Terminal> python add_input.py
operand 1: 1
operand 2: 3.0
<type 'int'> + <type 'float'> becomes <type 'float'>
with value 4
or two lists:
Terminal> python add_input.py
operand 1: [1,2]
operand 2: [-1,0,1]
<type 'list'> + <type 'list'> becomes <type 'list'>
with value [1, 2, -1, 0, 1]
This great flexibility also quickly breaks programs...¶
Terminal> python add_input.py
operand 1: (1,2)
operand 2: [3,4]
Traceback (most recent call last):
File "add_input.py", line 3, in <module>
r = i1 + i2
TypeError: can only concatenate tuple (not "list") to tuple
Terminal> python add_input.py
operand 1: one
Traceback (most recent call last):
File "add_input.py", line 1, in <module>
i1 = eval(raw_input('operand 1: '))
File "<string>", line 1, in <module>
NameError: name 'one' is not defined
Terminal> python add_input.py
operand 1: 4
operand 2: 'Hello, World!'
Traceback (most recent call last):
File "add_input.py", line 3, in <module>
r = i1 + i2
TypeError: unsupported operand type(s) for +: 'int' and 'str'
A similar magic function: exec¶
eval(s)evaluates an expressionseval('r = 1+1')is illegal because this is a statement, not only an expression...but we can use
execto turn one or more complete statements into live code:
statement = 'r = 1+1' # store statement in a string
exec(statement)
print r # prints 2
For longer code we can use multi-line strings:
somecode = '''
def f(t):
term1 = exp(-a*t)*sin(w1*x)
term2 = 2*sin(w2*x)
return term1 + term2
'''
exec(somecode) # execute the string as Python code
exec can be used for building a function at run-time¶
Embed user's formula in a Python function:
formula = raw_input('Write a formula involving x: ')
code = """
def f(x):
return %s
""" % formula
from math import * # make sure we have sin, cos, log, etc
exec(code) # turn string formula into live function
# Ask the user for x values and evaluate f(x)
x = 0
while x is not None:
x = eval(raw_input('Give x (None to quit): '))
if x is not None:
y = f(x)
print 'f(%g)=%g' % (x, y)
While the program is running, the user types a formula, which becomes a function, the user gives x values until the answer is None, and the program evaluates the function f(x). Note: the programmer knows nothing about the user's choice of f(x) when she writes the program (!).
StringFunction: turn string formulas into Python functions¶
It is common for programs to read formulas and turn them into functions so we have made a special tool for this purpose:
from scitools.std import StringFunction
formula = 'exp(x)*sin(x)'
f = StringFunction(formula)
f(0)
from math import pi
f(pi)
print str(f)
The function can also have parameters: $g(t) = Ae^{-at}\sin (\omega x)$
g = StringFunction('A*exp(-a*t)*sin(omega*x)',
independent_variable='t', A=1, a=0.1, omega=pi, x=5)
print g(1.2)
g.set_parameters(A=2, x=10)
print g(1.2)
Example: program for numerical differentiation¶
Usage:
Terminal> python diff.py 'exp(x)*sin(x)' 3.4
Numerical derivative: -36.6262969164
Differentiate $e^x\sin x$ at $x=3.4$ numerically.
Implementation:
import sys
from scitools.std import StringFunction
f = StringFunction(sys.argv[1], independent_variable='x')
x = float(sys.argv[2])
def numerical_derivative(f, x, h=1E-5):
return (f(x+h) - f(x-h))/(2*h)
print 'Numerical derivative:', numerical_derivative(f, x)
We can extend the program to also include symbolic differentiation¶
Terminal> python diff.py 'exp(x)*sin(x)' 3.4
Numerical derivative: -36.6262969164
Exact derivative: -36.6262969154476 (error=9.390E-10)
Formula for the derivative: exp(x)*sin(x) + exp(x)*cos(x)
Program extension:
import sympy as sym
x_value = x # store the value of x; x will be used as symbol
x = sym.symbols('x') # need x as symbol
formula = sym.sympify(str(f)) # turn f into sympy expression
# Differentiate formula wrt symbol x
dfdx = sym.diff(formula, x)
# Substitute symbol x by x_value
dfdx_value = dfdx.subs(x, x_value)
print 'Exact derivative:', dfdx_value, '(error=%.3E)' % \
(dfdx_value - numerical_derivative(f, x_value))
print 'Formula for the derivative:', dfdx
Example on reading 4 parameters from the command line¶
Input data: $s_0$ (initial location), $v_0$ (initial velocity), $a$ (constant acceleration) and $t$ (time)
Output data: $s$ (current location)
Specify $s_0=1$ m, $v_0=1$ m/s, $a=0.5$ $\hbox{m/s}^2$, and $t=3$ s on the command line:
Terminal> python location_cml.py 1 1 0.5 3
6.25
Program:
import sys
s0 = float(sys.argv[1])
v0 = float(sys.argv[2])
a = float(sys.argv[3])
t = float(sys.argv[4])
s = s0 + v0*t + 0.5*a*t*t
print s
Command-line arguments with options¶
Many programs, especially on Unix systems, take a set of command-line arguments of the form --option value
Terminal> python location.py --v0 1 --t 3 --s0 1 --a 0.5
Terminal> python location.py --t 3
The latter run relies on default values for v0, s0, and a:
we provide only the values we want to change.
Such option-value pairs make it easier to understand what the input is (cf. keyword arguments).
Programming option-value pairs with the argparse module¶
import argparse
parser = argparse.ArgumentParser()
# Define command-line arguments
parser.add_argument('--v0', '--initial_velocity', type=float,
default=0.0, help='initial velocity')
parser.add_argument('--s0', '--initial_position', type=float,
default=0.0, help='initial position')
parser.add_argument('--a', '--acceleration', type=float,
default=1.0, help='acceleration')
parser.add_argument('--t', '--time', type=float,
default=1.0, help='time')
# Read the command line and interpret the arguments
args = parser.parse_args()
# Extract values
s = args.s0 + args.v0*t + 0.5*args.a*args.t**2
# or
s0 = args.s0; v0 = args.v0; a = args.a; t = args.t
s = s0 + v0*t + 0.5*a*t**2
The program has long and short command-line arguments¶
Can use short or long options:
Terminal> python location.py --v0 1.2 --t 0.2
Terminal> python location.py --initial_velocity 1.2 --time 0.2
Graphical user interfaces¶
Most programs today fetch input data from graphical user interfaces (GUI), consisting of windows and graphical elements on the screen: buttons, menus, text fields, etc.
Why don't we learn to make such type of programs?
GUI demands much extra complicated programming
Experienced users often prefer command-line input
Programs with command-line or file input can easily be combined with each other, this is difficult with GUI-based programs
Assertion: command-line input will probably fill all your needs in university courses
But let's have a look at GUI programming!
A graphical Celsius-Fahrenheit conversion program¶

The Celsius degrees can be filled in as a number in a field
Clicking the "is" button computes the corresponding Fahrenheit temperature
The GUI code¶

from Tkinter import *
root = Tk()
C_entry = Entry(root, width=4)
C_entry.pack(side='left')
Cunit_label = Label(root, text='Celsius')
Cunit_label.pack(side='left')
def compute():
C = float(C_entry.get())
F = (9./5)*C + 32
F_label.configure(text='%g' % F)
compute = Button(root, text=' is ', command=compute)
compute.pack(side='left', padx=4)
F_label = Label(root, width=4)
F_label.pack(side='left')
Funit_label = Label(root, text='Fahrenheit')
Funit_label.pack(side='left')
root.mainloop()
Reading data from files¶
Scientific data are often available in files. We want to read the data into objects in a program to compute with the data.
Example on a data file.
21.8
18.1
19
23
26
17.8
One number on each line. How can we read these numbers?
f = open('data.txt', 'w')
f.write("""21.8
18.1
19
23
26
17.8
""")
f.close()
Reading a file line by line¶
Basic file reading:
infile = open('data.txt', 'r') # open file
for line in infile:
# do something with line
infile.close() # close file
Compute the mean values of the numbers in the file:
infile = open('data.txt', 'r') # open file
mean = 0
for line in infile:
number = float(line) # line is string
mean = mean + number
print 'number=%g' % g
mean = mean/len(lines)
print mean
Alternative ways to read a file¶
Read all lines at once into a list of strings (lines):
lines = infile.readlines()
for line in lines:
# process line
infile.close()
The modern with statement:
with open('data.txt', 'r') as infile:
for line in infile:
# process line
The old-fashioned while construction:
while True:
line = infile.readline()
if not line:
break
# process line
infile.close()
Reading the whole file into a string:
text = infile.read()
# process the string text
f = open('tmp.txt', 'w')
f.write("""Line 1.
Line 2.
Line 3.
Line 4.
""")
f.close()
Session:
infile = open('tmp.txt', 'r')
lines = infile.readlines() # read all lines
lines
infile.readline() # no more to read
infile = open('tmp.txt', 'r')
infile.readline() # read one line
infile.readline() # read next line
for line in infile: # read the next lines to the end
print line
More demo of file reading and string splitting¶
infile = open('tmp.txt', 'r')
filestr = infile.read()
filestr
filestr.split() # split out all words
line = 'Line 3.\n'
line.split()
line.split('e')
Most data files contain text mixed with numbers¶
File with data about rainfall:
Average rainfall (in mm) in Rome: 1188 months between 1782 and 1970
Jan 81.2
Feb 63.2
Mar 70.3
Apr 55.7
May 53.0
Jun 36.4
Jul 17.5
Aug 27.5
Sep 60.9
Oct 117.7
Nov 111.0
Dec 97.9
Year 792.9
How do we read such a file?
f = open('rainfall.txt', 'w')
f.write("""Average rainfall (in mm) in Rome: 1188 months between 1782 and 1970
Jan 81.2
Feb 63.2
Mar 70.3
Apr 55.7
May 53.0
Jun 36.4
Jul 17.5
Aug 27.5
Sep 60.9
Oct 117.7
Nov 111.0
Dec 97.9
Year 792.9
""")
f.close()
Reading a mixture of text and numbers¶
The key idea to process each line is to split the line into words:
months = []
values = []
for line in infile:
words = line.split() # split into words
if words[0] != 'Year':
months.append(words[0])
values.append(float(words[1]))
Can split with respect to any string s: line.split(s)
line = 'Oct 117.7'
words = line.split()
words
type(words[1]) # string, not a number!
Complete program for reading rainfall data¶
def extract_data(filename):
infile = open(filename, 'r')
infile.readline() # skip the first line
months = []
rainfall = []
for line in infile:
words = line.split()
# words[0]: month, words[1]: rainfall
months.append(words[0])
rainfall.append(float(words[1]))
infile.close()
months = months[:-1] # Drop the "Year" entry
annual_avg = rainfall[-1] # Store the annual average
rainfall = rainfall[:-1] # Redefine to contain monthly data
return months, rainfall, annual_avg
months, values, avg = extract_data('rainfall.dat')
print 'The average rainfall for the months:'
for month, value in zip(months, values):
print month, value
print 'The average rainfall for the year:', avg
Writing data to file¶
Basic pattern:
outfile = open(filename, 'w') # 'w' for writing
for data in somelist:
outfile.write(sometext + '\n')
outfile.close()
Can append text to a file with open(filename, 'a').
Example: Writing a table to file¶
Problem:
We have a nested list (rows and columns):
data = \
[[ 0.75, 0.29619813, -0.29619813, -0.75 ],
[ 0.29619813, 0.11697778, -0.11697778, -0.29619813],
[-0.29619813, -0.11697778, 0.11697778, 0.29619813],
[-0.75, -0.29619813, 0.29619813, 0.75 ]]
Write these data to file in tabular form
Solution:
outfile = open('tmp_table.dat', 'w')
for row in data:
for column in row:
outfile.write('%14.8f' % column)
outfile.write('\n')
outfile.close()
Resulting file:
0.75000000 0.29619813 -0.29619813 -0.75000000
0.29619813 0.11697778 -0.11697778 -0.29619813
-0.29619813 -0.11697778 0.11697778 0.29619813
-0.75000000 -0.29619813 0.29619813 0.75000000
What is a file?¶
A file is a sequence of characters
For simple text files, each character is one byte (=8 bits, a bit is 0 or 1), which gives $2^8=256$ different characters
(Text files in, e.g., Chinese and Japanese need several bytes for each character)
Save the text "ABCD" to file in Gedit/Emacs and OpenOffice/Word and examine the file!
File reading in Python is about either reading all characters (
read) or reading line by line (readline,readlines,for line in fileobj)
Back to a simple program that reads from the command line¶
Code:
import sys
C = float(sys.argv[1])
F = 5./9*C + 32
print F
Next topic:
How to handle wrong input from the user?
Our program stops with a strange error message if the command-line argument is missing¶
A user can easily use our program in a wrong way, e.g.,
Terminal> python c2f_cml.py
Traceback (most recent call last):
File "c2f_cml.py", line 2, in ?
C = float(sys.argv[1])
IndexError: list index out of range
Why?
The user forgot to provide a command-line argument
sys.argvhas then only one element,sys.argv[0], which is the program name (c2f_cml.py)Index 1, in
sys.argv[1], points to a non-existing element in thesys.argvlistAny index corresponding to a non-existing element in a list leads to
IndexError
We should handle errors in input!¶
How can we take control, explain what was wrong with the input, and stop the program without strange Python error messages?
# Program c2f_cml_if.py
import sys
if len(sys.argv) < 2:
print 'You failed to provide a command-line arg.!'
sys.exit(1) # abort
F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)
Terminal> python c2f_cml_if.py
You failed to provide a command-line arg.!
Exceptions as an alternative to if tests¶
Rather than test if something is wrong, recover from error, else do what we indended to do, it is common in Python (and many other languages) to try to do what we indend to, and if it fails, we recover from the error
This principle makes use of a
try-exceptblock
try:
<statements we intend to do>
except:
<statements for handling errors>
If something goes wrong in the try block, Python raises an exception and the execution jumps immediately to the except block.
The temperature conversion program with try-except¶
Try to read C from the command-line, if it fails, tell the user,
and abort execution:
import sys
try:
C = float(sys.argv[1])
except:
print 'You failed to provide a command-line arg.!'
sys.exit(1) # abort
F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)
Execution:
Terminal> python c2f_cml_except1.py
You failed to provide a command-line arg.!
Terminal> python c2f_cml_except1.py 21C
You failed to provide a command-line arg.!
It is good programming style to test for specific exceptions¶
It is good programming style to test for specific exceptions:
try:
C = float(sys.argv[1])
except IndexError:
print 'You failed to provide a command-line arg.!'
If we have an index out of bounds in sys.argv,
an IndexError exception is raised, and we jump to the except block.
If any other exception arises, Python aborts the execution:
Terminal> python c2f_cml_tmp.py 21C
Traceback (most recent call last):
File "tmp.py", line 3, in <module>
C = float(sys.argv[1])
ValueError: invalid literal for float(): 21C
Improvement: test for IndexError and ValueError exceptions¶
import sys
try:
C = float(sys.argv[1])
except IndexError:
print 'No command-line argument for C!'
sys.exit(1) # abort execution
except ValueError:
print 'C must be a pure number, not "%s"' % sys.argv[1]
sys.exit(1)
F = 9.0*C/5 + 32
print '%gC is %.1fF' % (C, F)
Executions:
Terminal> python c2f_cml_v3.py
No command-line argument for C!
Terminal> python c2f_cml_v3.py 21C
Celsius degrees must be a pure number, not "21C"
The programmer can raise exceptions¶
Instead of just letting Python raise exceptions, we can raise our own and tailor the message to the problem at hand
We provide two examples on this:
catching an exception, but raising a new one with an improved (tailored) error message
raising an exception because of wrong input data
Baisc syntax:
raise ExceptionType(message)
Examples on re-raising exceptions with better messages¶
def read_C():
try:
C = float(sys.argv[1])
except IndexError:
# re-raise, but with specific explanation:
raise IndexError(
'Celsius degrees must be supplied on the command line')
except ValueError:
# re-raise, but with specific explanation:
raise ValueError(
'Degrees must be number, not "%s"' % sys.argv[1])
# C is read correctly as a number, but can have wrong value:
if C < -273.15:
raise ValueError('C=%g is a non-physical value!' % C)
return C
Calling the previous function and running the program¶
try:
C = read_C()
except (IndexError, ValueError) as e:
# print exception message and stop the program
print e
sys.exit(1)
Executions:
Terminal> c2f_cml.py
Celsius degrees must be supplied on the command line
Terminal> c2f_cml.py 21C
Celsius degrees must be a pure number, not "21C"
Terminal> c2f_cml.py -500
C=-500 is a non-physical value!
Terminal> c2f_cml.py 21
21C is 69.8F
Making your own modules¶
We have frequently used modules like math and sys:
from math import log
r = log(6) # call log function in math module
import sys
x = eval(sys.argv[1]) # access list argv in sys module
Characteristics of modules:
Collection of useful data and functions (later also classes)
Functions in a module can be reused in many different programs
If you have some general functions that can be handy in more than one program, make a module with these functions
It's easy: just collect the functions you want in a file, and that's a module!
Case on making our own module¶
Here are formulas for computing with interest rates:
$A_0$: initial amount, $p$: percentage, $n$: days, $A$: final amount
We want to make a module with these four functions.
First we make Python functions for the formuluas¶
from math import log as ln
def present_amount(A0, p, n):
return A0*(1 + p/(360.0*100))**n
def initial_amount(A, p, n):
return A*(1 + p/(360.0*100))**(-n)
def days(A0, A, p):
return ln(A/A0)/ln(1 + p/(360.0*100))
def annual_rate(A0, A, n):
return 360*100*((A/A0)**(1.0/n) - 1)
Then we can make the module file¶
Collect the 4 functions in a file
interest.pyNow
interest.pyis actually a moduleinterest(!)
Write the module code to file:
with open('interst.py', 'w') as outfile:
outfile.write("""
from math import log as ln
def present_amount(A0, p, n):
return A0*(1 + p/(360.0*100))**n
def initial_amount(A, p, n):
return A*(1 + p/(360.0*100))**(-n)
def days(A0, A, p):
return ln(A/A0)/ln(1 + p/(360.0*100))
def annual_rate(A0, A, n):
return 360*100*((A/A0)**(1.0/n) - 1)
""")
Example on use:
# How long time does it take to double an amount of money?
from interest import days
A0 = 1; A = 2; p = 5
n = days(A0, 2, p)
years = n/365.0
print 'Money has doubled after %.1f years' % years
Adding a test block in a module file¶
Module files can have an if test at the end containing a test block for testing or demonstrating the module
The test block is not executed when the file is imported as a module in another program
The test block is executed only when the file is run as a program
if __name__ == '__main__': # this test defineds the test block
<block of statements>
In our case:
if __name__ == '__main__':
A = 2.2133983053266699
A0 = 2.0
p = 5
n = 730
print 'A=%g (%g) A0=%g (%.1f) n=%d (%d) p=%g (%.1f)' % \
(present_amount(A0, p, n), A,
initial_amount(A, p, n), A0,
days(A0, A, p), n,
annual_rate(A0, A, n), p)
Test blocks are often collected in functions¶
Let's make a real test function for what we had in the test block:
def test_all_functions():
# Define compatible values
A = 2.2133983053266699; A0 = 2.0; p = 5; n = 730
# Given three of these, compute the remaining one
# and compare with the correct value (in parenthesis)
A_computed = present_amount(A0, p, n)
A0_computed = initial_amount(A, p, n)
n_computed = days(A0, A, p)
p_computed = annual_rate(A0, A, n)
def float_eq(a, b, tolerance=1E-12):
"""Return True if a == b within the tolerance."""
return abs(a - b) < tolerance
success = float_eq(A_computed, A) and \
float_eq(A0_computed, A0) and \
float_eq(p_computed, p) and \
float_eq(n_computed, n)
assert success # could add message here if desired
if __name__ == '__main__':
test_all_functions()
How can Python find our new module?¶
If the module is in the same folder as the main program, everything is simple and ok
Home-made modules are normally collected in a common folder, say
/Users/hpl/lib/python/mymodsIn that case Python must be notified that our module is in that folder
Technique 1: add folder to PYTHONPATH in .bashrc:
export PYTHONPATH=$PYTHONPATH:/Users/hpl/lib/python/mymods
Technique 2: add folder to sys.path in the program:
sys.path.insert(0, '/Users/hpl/lib/python/mymods')
Technique 3: move the module file in a directory that Python already searches for libraries.
Summary of reading from the keyboard and command line¶
Question and answer input:
var = raw_input('Give value: ') # var is string!
# if var needs to be a number:
var = float(var)
# or in general:
var = eval(var)
Command-line input:
import sys
parameter1 = eval(sys.argv[1])
parameter3 = sys.argv[3] # string is ok
parameter2 = eval(sys.argv[2])
Recall: sys.argv[0] is the program name
Summary of reading options-value pairs¶
--option value pairs with the aid of argparse:
import argparse
parser = argparse.ArgumentParser()
parser.add_argument('--p1', '--parameter_1', type=float,
default=0.0, help='1st parameter')
parser.add_argument('--p2', type=float,
default=0.0, help='2nd parameter')
args = parser.parse_args()
p1 = args.p1
p2 = args.p2
On the command line we can provide any or all of these options:
Terminal> program prog.py --parameter_1 2.1 --p2 -9
Summary of eval and exec¶
Evaluating string expressions with eval:
x = 20
r = eval('x + 1.1')
r
type(r)
Executing strings with Python code, using exec:
exec("""
def f(x):
return %s
""" % sys.argv[1])
Summary of exceptions¶
Handling exceptions:
try:
<statements>
except ExceptionType1:
<provide a remedy for ExceptionType1 errors>
except ExceptionType2, ExceptionType3, ExceptionType4:
<provide a remedy for three other types of errors>
except:
<provide a remedy for any other errors>
...
Raising exceptions:
if z < 0:
raise ValueError(
'z=%s is negative - cannot do log(z)' % z)
Summary of file reading and writing¶
infile = open(filename, 'r') # read
outfile = open(filename, 'w') # write
outfile = open(filename, 'a') # append
# Reading
line = infile.readline() # read the next line
filestr = infile.read() # read rest of file into string
lines = infile.readlines() # read rest of file into list
for line in infile: # read rest of file line by line
# Writing
outfile.write(s) # add \n if you need it
# Closing
infile.close()
outfile.close()
A summarizing example: solving $f(x)=0$¶
Nonlinear algebraic equations like
are usually impossible to solve by pen and paper, but can be solved by numerical methods. To this end, rewrite any equation as
For the above we have (put everything on the left-hand side)
We shall learn about a method for solving $f(x)=0$¶
A solution $x$ of $f(x)=0$ is called a root of $f(x)$
Outline of the next slides:
Formulate a method for finding a root
Translate the method to a precise algorithm
Implement the algorithm in Python
Test the implementation
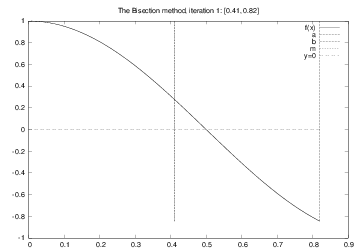
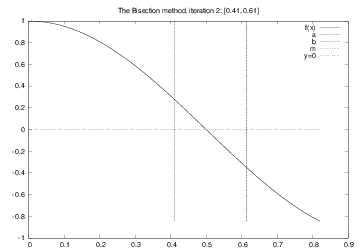
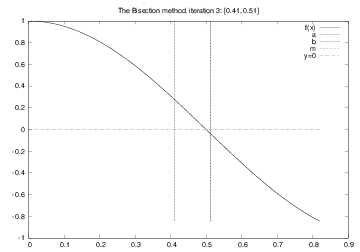
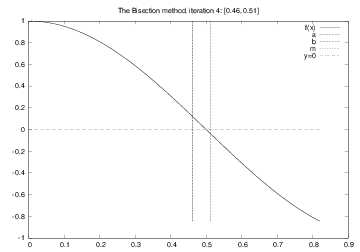
The Bisection method¶
Start with an interval $[a,b]$ in which $f(x)$ changes sign
Then there must be (at least) one root in $[a,b]$
Halve the interval:
$m=(a+b)/2$; does $f$ change sign in left half $[a,m]$?
Yes: continue with left interval $[a,m]$ (set $b=m$)
No: continue with right interval $[m,b]$ (set $a=m$)
Repeat the procedure
After halving the initial interval $[p,q]$ $n$ times, we know that $f(x)$ must have a root inside a (small) interval $2^{-n}(q-p)$
The method is slow, but very safe
Other methods (like Newton's method) can be faster, but may also fail to locate a root - bisection does not fail
Solving $\cos \pi x =0$: iteration no. 1¶
Solving $\cos \pi x =0$: iteration no. 2¶
Solving $\cos \pi x =0$: iteration no. 3¶
Solving $\cos \pi x =0$: iteration no. 4¶
From method description to a precise algorithm¶
We need to translate the mathematical description of the Bisection method to a Python program
An important intermediate step is to formulate a precise algorithm
Algorithm = detailed, code-like formulation of the method
for i in range(0, n+1):
m = (a + b)/2
if f(a)*f(m) <= 0:
b = m # root is in left half
else:
a = m # root is in right half
# f(x) has a root in [a,b]
The algorithm can be made more efficient¶
$f(a)$ is recomputed in each if test
This is not necessary if $a$ has not changed since last pass in the loop
On modern computers and simple formulas for $f(x)$ these extra computations do not matter
However, in science and engineering one meets $f$ functions that take hours or days to evaluate at a point, and saving some $f(a)$ evaluations matters!
Rule of thumb: remove redundant computations (unless the code becomes much more complicated, and harder to verify)
New, more efficient version of the algorithm¶
Idea: save $f(x)$ evaluations in variables
f_a = f(a)
for i in range(0, n+1):
m = (a + b)/2
f_m = f(m)
if f_a*f_m <= 0:
b = m # root is in left half
else:
a = m # root is in right half
f_a = f_m
# f(x) has a root in [a,b]
How to choose $n$? That is, when to stop the iteration¶
We want the error in the root to be $\epsilon$ or smaller
After $n$ iterations, the initial interval $[a,b]$ is halved $n$ times and the current interval has length $2^{-n}(b-a)$. This is sufficiently small if $2^{-n}(b-a) = \epsilon \quad\Rightarrow\quad n = - {\ln\epsilon -\ln (b-a)\over\ln 2}$
A simpler alternative: just repeat halving until the length of the current interval is $\leq\epsilon$
This is easiest done with a while loop:
while b-a <= epsilon:We also add a test to check if $f$ really changes sign in the initial inverval $[a,b]$
Final version of the Bisection algorithm¶
f_a=f(a)
if f_a*f(b) > 0:
# error: f does not change sign in [a,b]
i = 0
while b-a > epsilon:
i = i + 1
m = (a + b)/2
f_m = f(m)
if f_a*f_m <= 0:
b = m # root is in left half
else:
a = m # root is in right half
f_a = f_m
# if x is the real root, |x-m| < epsilon
Python implementation of the Bisection algorithm¶
def f(x):
return 2*x - 3 # one root x=1.5
eps = 1E-5
a, b = 0, 10
fa = f(a)
if fa*f(b) > 0:
print 'f(x) does not change sign in [%g,%g].' % (a, b)
sys.exit(1)
i = 0 # iteration counter
while b-a > eps:
i += 1
m = (a + b)/2.0
fm = f(m)
if fa*fm <= 0:
b = m # root is in left half of [a,b]
else:
a = m # root is in right half of [a,b]
fa = fm
x = m # this is the approximate root
Implementation as a function (more reusable!)¶
def bisection(f, a, b, eps):
fa = f(a)
if fa*f(b) > 0:
return None, 0
# Alternative: raise ValueError(
# 'No change of sign in [%g,%g]' % (a, b))
i = 0 # iteration counter
while b-a > eps:
i += 1
m = (a + b)/2.0
fm = f(m)
if fa*fm <= 0:
b = m # root is in left half of [a,b]
else:
a = m # root is in right half of [a,b]
fa = fm
return m, i
print bisection(f=lambda x: 2*x-3, a=0, b=10, eps=1E-5)
Make a module of this function¶
If we put the
bisectionfunction in a filebisection.py, we automatically have a module, and thebisectionfunction can easily be imported in other programs to solve $f(x)=0$We should make a test function too
def test_bisection():
def f(x):
return 2*x - 3 # only one root x=1.5
eps = 1E-5
x, iter = bisection(f, a=0, b=10, eps=eps)
success = abs(x - 1.5) < eps # test within eps tolerance
assert success, 'found x=%g != 1.5' % x
if __name__ == '__main__':
test_bisection()
To the point of this lecture: get input!¶
We want to provide an $f(x)$ formula at the command line along with $a$ and $b$ (3 command-line args)
Usage:
Terminal> python bisection.py 'sin(pi*x**3)-x**2' -1 3.5
Reading input:
def get_input():
"""Get f, a, b, eps from the command line."""
from scitools.std import StringFunction
f = StringFunction(sys.argv[1])
a = float(sys.argv[2])
b = float(sys.argv[3])
eps = float(sys.argv[4])
return f, a, b, eps
# Usage:
f, a, b, eps = get_input()
x, iter = bisection(f, a, b, eps)
print 'Found root x=%g in %d iterations' % (x, iter)
Improvements: error handling¶
def get_input():
"""Get f, a, b, eps from the command line."""
from scitools.std import StringFunction
try:
f = StringFunction(sys.argv[1])
a = float(sys.argv[2])
b = float(sys.argv[3])
eps = float(sys.argv[4])
except IndexError:
print 'Usage %s: f a b eps' % sys.argv[0]
sys.exit(1)
return f, a, b, eps
Applications of the Bisection method¶
Two examples: $\tanh x = x$ and $\tanh x^5 = x^5$:
Terminal> python bisection_plot.py "x-tanh(x)" -1 1
Terminal> python bisection_plot.py "x**5-tanh(x**5)" -1 1
The first equation is easy to treat, but the second leads to much less accurate results. Why??