Deep XOR¶
The goal of this notebook is to illustrate, step by step, the modelling of an XOR gate using a simple neural network trained via gradient descent.
This is basically a little exercise I decided to go through to have a better understanding of how neural networks work. Here you'll find the derivation of all necessary equations and their implementation in numpy. Hopefully it may help other practitioners too. Life is sharing (openly on github) :)
(The whole thing is inspired by Section 6.2 of the absolutely fantastic The Deep Learning Book, and this)
import numpy as np # That's all we need :)
The Data¶
We randomly generate a handful of examples to later train our model. There are only 4 different unique input combinations to XOR:
- $0 \oplus 0 = 0$
- $0 \oplus 1 = 1$
- $1 \oplus 0 = 1$
- $1 \oplus 1 = 0$
Thus, $N$ observations randomly sampled from these 4 pairs of ones and zeroes are generated and stored in $X \in \mathbb{N}^{N \times 2}$, and passed through the XOR operation to obtain the target set of labels $Y \in \mathbb{N}^{N \times 2}$, which we encode as one-hot vectors.
def gen_data(N):
"""Generates an XOR dataset using one-hot vector encoding.
Parameters
----------
N: int
Number of observations to be generated.
Returns
-------
X: np.ndarray((N, 2))
Matrix containing an observation per row, representing the input
to the XOR operation (observations).
Y: np.ndarray((N, 2))
Result of the XOR operation for each row, encoded with
one-hot vector per row (targets).
"""
X = np.random.randint(0, 2, size=(N, 2))
Y = np.zeros((N, 2))
Y[np.arange(N), [int(np.logical_xor(x[0], x[1])) for x in X]] = 1
return X, Y
def xor_print(X, Y, N):
"""Prints out an XOR dataset.
Parameters
----------
X: np.ndarray((N, 2))
Observations.
Y: np.ndarray((N, 2))
Targets.
N: int
Number of observations to be printed.
"""
[print(str(x[0]) + ' XOR ' + str(x[1]) + ' = ' + str(np.argmax(y)))
for x, y in zip(X[:N], Y[:N])]
The Model¶
To approximate the XOR function, which is non-linear, we need a non-linear model (see the bonus section at the end of this notebook if you're curious to know why). Since neural networks are so cool, we design a feedforward neural network with a single hidden layer (ok, that's not too deep, but nowadays it seems almost impossible to write something interesting without this magic word in it, hence the title of this notebook).
The network has two output units $\hat{y}_1$ and $\hat{y}_2$, representing the likelihood of having a 0 or a 1, respectively, thus framing the problem as classification. The network diagram may look as follows:
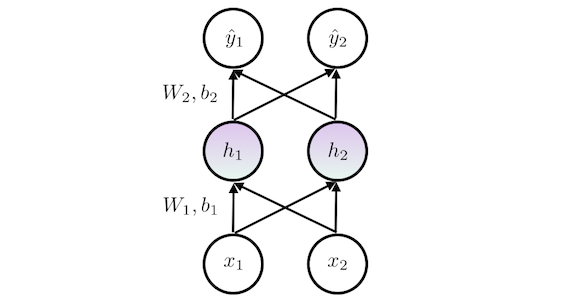
Where the weights $W_1, W_2$ and basis $b_1, b_2$ are the coefficients to be learned, $\mathbf{x} = \{x_1, x_2\}$ is the input, $\mathbf{h} = \{h_1, h_2\}$ is the content of the hidden layer, and $\mathbf{\hat{y}} = \{\hat{y}_1, \hat{y}_2\}$ is the output of the network.
Each layer is composed by a standard affine transformation plus its non-linear activation. We use a rectified linear unit (ReLU) $\sigma$ for the activation of the hidden layer. Formally:
$$\mathbf{h} = \sigma(\mathbf{x}^T W_1 + b_1) = \text{max}\{\mathbf{0}, \mathbf{x}^T W_1 + b_1\}$$For the output layer, we use the standard softmax function, which is the common activation used for classification problems. To simplify the math, we decompose the output layer into its linear equation and its activation:
$$\begin{equation} \mathbf{z} = \mathbf{h}^T W_2 + b_2 \\ \mathbf{\hat{y}} = \frac{e^\mathbf{z}}{\sum_j^2 e^{z_j}} \end{equation}$$Note how the denominator of the softmax function sums only twice: once for each class (i.e., 0 and 1). This function essentially squashes the predictions and then normalizes them, thus yielding a set of proper probabilities.
Multiple Inputs¶
If we focus on multiple observations $X = \{\mathbf{x}_1^T, \mathbf{x}_2^T, \ldots, \mathbf{x}_N^T\}$ instead of a single one $\mathbf{x}_i$ we can rewrite the equations as follows:
$$\begin{equation} H = \sigma(X W_1 + b_1) = \text{max}\{\mathbf{0}, X W_1 + b_1\} \\ Z = H W_2 + b_2\\ \hat{Y} = \frac{e^Z}{\sum_j^2 e ^{\mathbf{z}_j}} \end{equation}$$where the biases $b_1, b_2$ are broadcasted across their respective inputs.
We can now implement a function that computes a multiple input forward pass of the network using numpy:
def forward_pass(X, W1, W2, b1, b2):
"""Computes a forward pass of the network. Once the coefficients are trained,
this should compute the XOR on all x \in X.
Parameters
----------
X: np.ndarray((N, 2))
Inputs to the network.
W1: np.ndarray((2, n_hidden))
Set of weights for the first layer.
W2: np.ndarray((n_hidden, 2))
Set of weights for the second layer.
b1: np.ndarray((1, n_hidden))
Bias for the first layer.
b2: np.ndarray((1, 2))
Bias for the second layer.
Returns
-------
H: np.ndarray((N, n_hidden))
Content of the hidden layer.
Y_est: np.ndarray((N, 2))
Output of the network, the two columns represent the likelihood of
having a 0 or a 1, in this order.
"""
# Hidden layer forward pass
H = np.maximum(0, np.dot(X, W1) + b1) # ReLU activation
# Second layer forward pass without activation
linear = np.dot(H, W2) + b2
# Softmax activation (output)
Y_est = np.exp(linear) / np.sum(np.exp(linear), axis=1, keepdims=True) # [N x 2]
return H, Y_est
The Initialization¶
We can initialize our training coefficients randomly (there are fancier ways, but this problem is not that sophisticated after all). Notice how it would be straightforward to include more hidden units in our hidden layer by just changing the n_hidden argument. Feel free to play with this parameter, it seems to converge faster with 3 or 4 units. But for now, let's stick to our original model of 2 hidden units.
def init_coefficients(n_hidden=2):
"""Initializes the training coefficients randomly.
Parameters
----------
n_hidden: int > 0
Number of hidden layers.
Returns
-------
W1: np.ndarray((2, n_hidden))
Set of weights for the first layer.
W2: np.ndarray((n_hidden, 2))
Set of weights for the second layer.
b1: np.ndarray((1, n_hidden))
Bias for the first layer.
b2: np.ndarray((1, 2))
Bias for the second layer.
"""
# Input -> Hidden layer weights and bias
W1 = np.random.random(size=(2, n_hidden))
b1 = np.zeros((1, n_hidden)) # bias
# Hidden -> Output layer weights and bias
W2 = np.random.random(size=(n_hidden, 2))
b2 = np.zeros((1, 2)) # bias
return W1, b1, W2, b2
The Loss Function¶
Next step is to define an appropriate differentiable loss function that allows us to train our network. The loss should be small when we are obtaining successful results with the current parameters, and high otherwise.
The cross-entropy function is commonly used in classification problems, since its derivative is quite simple and yet successfully captures the cost of the network for a given set of parameters.
The average cross-entropy is defined as:
$$L = - \frac{1}{N}\sum_{i}^N \sum_{j}^2 y_{ij} \log(\hat{y}_{ij}) $$Let's quickly inspect this function. If we have a perfect prediction (e.g., $\mathbf{y}_i = \{0, 1\}$ and $\mathbf{\hat{y}}_i = \{0, 1\}$), then $L_i$ is 0, as desired. Whereas, if we have completely wrong one (e.g., $\mathbf{y}_i = \{0, 1\}$ and $\mathbf{\hat{y}}_i = \{1, 0\}$), then we get $L_i = \infty$, also as required. Alrighten.
We can now implement this function in numpy. To avoid the instability of computing $\log(0)$, we can simply multiply each of the predicted results with the target value, and sum across them (one will be zero). This is essentially like "selecting" the likelihood of the correct class:
$$L = - \frac{1}{N}\sum_{i}^N y_{ik} \log(\hat{y}_{ik}) + (1 - y_{ik}) \log(\hat{y}_{in}) = - \frac{1}{N}\sum_{i}^N \log(\hat{y}_{ik}) \qquad\text{where}\qquad y_{ik} = 1$$And here its implementation:
def compute_loss(Y, Y_est):
"""Computes the averate cross-entropy loss.
Parameters
----------
Y: np.ndarray((N, 2))
Target labels (XOR correct results).
Y_est: np.ndarray((N, 2))
Estimated XOR values.
Returns
-------
loss: float
Loss value: the average cross-entropy.
"""
N = Y.shape[0]
return - np.sum(np.log(np.sum(Y * Y_est, axis=1))) / float(N)
The Training¶
As it is common in neural networks, we use gradient descent to train our set of weights $W_1, W2$ and biases $b_1, b_2$. This method makes use of the partial derivates of the whole model to identify the steepest direction (the gradient) of each trainable variable in order to minimize, step by step, the given loss function $L$.
The chain-rule formula will help us in this process, backpropagating the gradient from the output of the network to its input. So, let us begin.
Gradient of the output layer¶
The (fun) derivative of our loss function with respect to the softmax output of our model is:
$$\begin{split} \frac{\partial L}{\partial z_{ij}} & = \frac{\partial L}{\partial \hat{y}_{ij}} \frac{\partial \hat{y}_{ij}}{\partial z_{ij}} \\ & = \frac{\partial}{\partial\hat{y}_{ij}} \left( - \sum_{j}^2 y_{ij} \log(\hat{y}_{ij}) \right) \frac{\partial \hat{y}_{ij}}{\partial z_{ij}}\\ & = - \sum_{j}^2 y_{ij} \frac{1}{\hat{y}_{ij}} \frac{\partial \hat{y}_{ij}}{\partial z_{ij}} \\ & = - \sum_{j}^2 y_{ij} \frac{1}{\hat{y}_{ij}} \frac{\partial}{\partial z_{ij}} \frac{e^{z_{ij}}}{\sum_m^2e^{z_{im}}} \\ & = - \sum_{j}^2 y_{ij} \frac{1}{\hat{y}_{ij}} \frac{e^{z_{ij}}\sum_m^2 e^{z_{im}} - e^{z_{ij}}e^{z_{ij}}}{(\sum_m^2e^{z_{im}})^2} \\ & = - y_{ik} \frac{1}{\hat{y}_{ik}} \frac{e^{z_{ik}}\sum_m^2 e^{z_{im}} - e^{z_{ik}}e^{z_{ik}}}{(\sum_m^2e^{z_{im}})^2} - (1 - y_{ik}) \frac{1}{\hat{y}_{in}} \frac{e^{z_{in}}\sum_m^2 e^{z_{im}} - e^{z_{in}}e^{z_{in}}}{(\sum_m^2e^{z_{im}})^2}\\ & = - y_{ik} \frac{1}{\hat{y}_{ik}} \frac{e^{z_{ik}}}{\sum_m^2e^{z_{im}}} \frac{\sum_m^2 e^{z_{im}} - e^{z_{ik}}}{\sum_m^2e^{z_{im}}}\\ & = - y_{ik} \frac{1}{\hat{y}_{ik}} \hat{y}_{ik} \frac{\sum_m^2 e^{z_{im}} - e^{z_{ik}}}{\sum_m^2e^{z_{im}}} \\ & = - y_{ik} \left( \frac{\sum_m^2 e^{z_{im}}}{\sum_m^2e^{z_{im}}} - \frac{e^{z_{ik}}}{\sum_m^2e^{z_{im}}} \right)\\ & = - y_{ik} ( 1 - \hat{y}_{ik})\\ & = - y_{ik} + y_{ik}\hat{y}_{ik}\\ & = - y_{ij} + 1\hat{y}_{ij}\\ & = \hat{y}_{ij} - y_{ij}\\ \end{split}$$Applied to all our datapoints, the result would be:
$$\begin{equation} \frac{\partial L}{\partial \mathbf{z}_{j}} = - \frac{1}{N} \frac{\partial}{\partial \mathbf{z}_{j}} \sum_{j}^2 \mathbf{y}_{j} \odot \log(\mathbf{\hat{y}}_{j}) = \frac{\mathbf{\hat{y}}_{j} - \mathbf{y}_{j}}{N}\\ \frac{\partial L}{\partial Z} = \frac{\hat{Y} - Y}{N} \end{equation}$$where $\odot$ is the element-wise product. Let's implement this in numpy:
def compute_loss_diff(Y, Y_est):
"""Computes the averate cross-entropy loss derivative.
Parameters
----------
Y: np.ndarray((N, 2))
Target labels (XOR correct results).
Y_est: np.ndarray((N, 2))
Estimated XOR values.
Returns
-------
dloss: np.ndarray((N, 2))
Loss value: the average cross-entropy derivative.
"""
return (Y_est - Y) / float(Y.shape[0])
Gradient of the hidden layer¶
We have computed the partial derivative with respect to our last layer, now let's do the same with respect to our hidden layer. This will help us when obtaining the partial derivatives to our trainable coefficients, which is ultimately what we want to obtain.
Again, let's apply the chain-rule to derive this:
$$\begin{split} \frac{\partial L}{\partial H} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial H} \\ & = \frac{\hat{Y} - Y}{N} \frac{\partial Z}{\partial H} \\ & = \frac{\hat{Y} - Y}{N} \frac{\partial}{\partial H} H W_2 + b_2 \\ & = \frac{\hat{Y} - Y}{N} W_2^T\\ \end{split}$$Including the ReLU activation function $\sigma$ from the first layer will simplify the math later for backpropagation, let's do it:
$$\begin{split} \frac{\partial L}{\partial \sigma} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial H}\frac{\partial H}{\partial \sigma} \\ & = \frac{\hat{Y} - Y}{N} W_2^T \frac{\partial H}{\partial \sigma}\\ & = \frac{\hat{Y} - Y}{N} W_2^T \frac{\partial}{\partial \sigma}\sigma(X W_1 + b_1)\\ & = \frac{\hat{Y} - Y}{N} W_2^T \frac{\partial}{\partial \sigma}\text{max}\{\mathbf{0}, X W_1 + b_1\}\\ & = \frac{\hat{Y} - Y}{N} W_2^T \mathbb{1}\{X W_1 + b_1 > 0\}\\ \end{split}$$As you can see, the derivative of a ReLu function $\mbox{max}\{0, x\}$ is simply the indicator $\mathbb{1}\{x > 0\}$. If this is not obvious, here's a further explanation.
Since we know that this $\mathbb{1}\{X W_1 + b_1 > 0\}$ will always be true as long as $\mathbb{1}\{H > 0\}$ is true (since $H$ is already rectified), we can further simplify the formula by:
$$\begin{split} \frac{\partial L}{\partial \sigma} = \frac{\hat{Y} - Y}{N} W_2^T \mathbb{1}\{X W_1 + b_1 > 0\} = \frac{\hat{Y} - Y}{N} W_2^T \mathbb{1}\{H > 0\}\\ \end{split}$$Let's put this derivative in a function.
def compute_hidden_diff(H, W2, dloss):
"""Computes the derivative of the first hidden layer, including it's activation.
Parameters
----------
H: np.ndarray((N, n_hidden))
Output of the hidden layer.
W2: np.ndarray((n_hidden, 2))
Coefficients of the hidden to output layer.
dloss: np.ndarray((N, 2))
Derivative of the output layer.
Returns
-------
dhidden: np.ndarray((N, n_hidden))
Derivative of the hidden layer.
"""
dhidden = np.dot(dloss, W2.T)
dhidden[H <= 0] = 0 # ReLU backprop
return dhidden
Gradient of the trainable coefficients¶
Now that we have the derivative of the loss function with respect to the output (second layer), we can easily compute the gradient of the trainable coefficients $W_2$ and $b_2$ using backpropagation. Let's do it:
$$\begin{split} \frac{\partial L}{\partial W_2} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial W_2} \\ & = \frac{\hat{Y} - Y}{N} \frac{\partial Z}{\partial W_2} \\ & = \frac{\hat{Y} - Y}{N} \frac{\partial}{\partial W_2} H W_2 + b_2 \\ & = H^T \frac{\hat{Y} - Y}{N}\\ \\ \frac{\partial L}{\partial b_2} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial b_2} \\ & = \frac{\hat{Y} - Y}{N} \frac{\partial}{\partial b_2} H W_2 + b_2 \\ & = \frac{\hat{Y} - Y}{N}\\ \end{split}$$Analogously, since we have computed the derivative of the loss function with respect to the hidden layer, we can now compute the one with respect to the rest of trainable coefficients $W_1$ and $b_1$:
$$\begin{split} \frac{\partial L}{\partial W_1} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial H}\frac{\partial H}{\partial \sigma}\frac{\partial \sigma}{\partial W_1} \\ & = \frac{\partial L}{\partial \sigma} \frac{\partial}{\partial W_1} X W_1 + b_1\\ & = X^T \frac{\partial L}{\partial \sigma}\\ & = X^T \frac{\hat{Y} - Y}{N} W_2^T \mathbb{1}\{H > 0\}\\ \\ \frac{\partial L}{\partial b_1} & = \frac{\partial L}{\partial \hat{Y}} \frac{\partial \hat{Y}}{\partial Z} \frac{\partial Z}{\partial H}\frac{\partial H}{\partial \sigma}\frac{\partial \sigma}{\partial b_1} \\ & = \frac{\partial L}{\partial \sigma} \frac{\partial}{\partial b_1} X W_1 + b_1\\ & = \frac{\partial L}{\partial \sigma}\\ & = \frac{\hat{Y} - Y}{N} W_2^T \mathbb{1}\{H > 0\}\\ \end{split}$$All of which could be modularized and implemented in a backpropagation function like this:
def backprop(x, dx):
"""Computes the backpropagation for a given layer.
Parameters
----------
x: np.ndarray((N, n_in))
Input layer.
dx: np.ndarray((N, n_out))
Derivative of the input layer.
Returns
-------
dW: np.ndarray((n_in, n_out))
Derivative of the loss with respect to the W matrix.
db: np.ndarray((1, n_out))
Derivative of the loss with respect to b.
"""
dW = np.dot(x.T, dx)
db = np.sum(dx, axis=0, keepdims=True)
return dW, db
Gradient Descent¶
Almost done! We now can use the gradients with respect to the trainable coefficients computed above to update the actual trainable coefficients step by step. This will be done iteratively, with a specific learning rate $\gamma$, until convergence.
Here the formula, applied to all $\mathcal{W} \in \{W_1, b_1, W_2, b_2\}$:
$$\mathcal{W} := \mathcal{W} - \gamma \frac{\partial L}{\partial \mathcal{W}}$$Let's write a function to do so:
def update_step(x, dx, step):
"""Update step of gradient descent. Updates the trainable coefficients.
Parameters
----------
x: np.ndarray
Trainable coefficient.
dx: np.ndarray
Derivative of the loss with respect to the trainable coefficient.
step: float
Step size of gradient descent.
Returns
-------
nx: np.ndarray
Updated trainable coefficient in the direction of its gradient.
"""
return x - step * dx
The Whole Thing¶
Alrighten. The last thing to do is to put all the pieces together. We will do so in a single training loop, that will go over a few thousand epochs.
It may be interesting to play around with the step variable, to see how much faster (but more likely to fall into bad local minima) the whole thing will be if set high enough; and how slow (but less likely to fall into those terrible places) it would be with a sufficiently small step.
In the last line of this implementation I update the whole training set with new randomly generated data. While this is not necessary (and makes the whole training noticeably slower), it seems to help to obtain better results. Feel free to play with it (i.e., remove it or just update the set after a few epochs).
Another interesting parameter is the number of training observations N. While it often converges with 100 observations, that's not always the case. I guess the more observations, the more local minima around the gradient we'll find, but it might result in a faster convergence too (when it does converge). Also notice how sensible this parameter is in terms of computation efficiency.
# Create some training data
N = 100
X, Y = gen_data(N)
# Initialize the coefficients randomly
W1, b1, W2, b2 = init_coefficients()
# Learning parameters
n_epochs = 10000
step = 0.01
# Main training loop
for n_epoch in range(n_epochs):
# Forward pass of the network, catching the two layers' outputs
H, Y_est = forward_pass(X, W1, W2, b1, b2)
# Average cross-entropy loss
loss = compute_loss(Y, Y_est)
# Gradient of the second (output) layer
dloss = compute_loss_diff(Y, Y_est)
# Gradient of the hidden layer
dhidden = compute_hidden_diff(H, W2, dloss)
# Backpropagation over all trainable coefficients
dW2, db2 = backprop(H, dloss)
dW1, db1 = backprop(X, dhidden)
# Update step
W1 = update_step(W1, dW1, step)
b1 = update_step(b1, db1, step)
W2 = update_step(W2, dW2, step)
b2 = update_step(b2, db2, step)
# Printout
if n_epoch % 1000 == 0:
acc = np.sum(Y[np.arange(N), np.argmax(Y_est, axis=1)]) / float(N) # Accuracy
print("\tEpoch %d: loss %f\t acc %.1f%%" % (n_epoch, loss, (acc * 100)))
# Generate more data randomly (this might prevent falling into bad local minima)
X, Y = gen_data(N)
Epoch 0: loss 0.684157 acc 80.0% Epoch 1000: loss 0.671128 acc 100.0% Epoch 2000: loss 0.555213 acc 100.0% Epoch 3000: loss 0.374493 acc 100.0% Epoch 4000: loss 0.198592 acc 100.0% Epoch 5000: loss 0.114024 acc 100.0% Epoch 6000: loss 0.074607 acc 100.0% Epoch 7000: loss 0.052104 acc 100.0% Epoch 8000: loss 0.045177 acc 100.0% Epoch 9000: loss 0.029315 acc 100.0%
The Test¶
Finally, we can generate more data and see how well the model generalizes. You should get 100% in most trained models if you use the default parameters from the cell above.
X_test, Y_test = gen_data(N)
_, Y_est = forward_pass(X_test, W1, W2, b1, b2)
acc = np.sum(Y_test[np.arange(N), np.argmax(Y_est, axis=1)]) / float(N)
print("Accuracy in Test set: %.2f%%" % (acc * 100))
# Let's print some of our Deep XOR results, just for fun
xor_print(X_test, Y_est, 10)
Accuracy in Test set: 100.00% 1 XOR 1 = 0 0 XOR 1 = 1 0 XOR 1 = 1 0 XOR 0 = 0 0 XOR 0 = 0 0 XOR 0 = 0 1 XOR 0 = 1 1 XOR 1 = 0 0 XOR 0 = 0 0 XOR 0 = 0
The End¶
So that's it. We have trained a feedwordard neural network with a hidden layer to model an XOR gate. We have implemented it using numpy. And it worked (at least most of the times).
I'm pretty sure there might be some bugs in the code / math. But that's why this is here, to learn with you, titans. Thus, pull requests are welcome :)
Bonus: XOR, Y U Not Work With Linear Models?¶
As explained in Section 6.2 of the Deep Learning book, the XOR operation is not linear. Therefore, it is not possible to model it with simple linear regression. To illustrate this, we can actually try to fit one of these simple models and find the results analytically.
We are gonna frame this as regression (instead of classification), so let's say that $\mathbf{y} \in \mathbb{R}^N$ are the labels (notice how this is now a simple vector instead of an $N \times 2$ matrix) and $X \in \mathbb{R}^{N \times 2}$ the observations set (as before). The model we want to approximate is:
$$ \mathbf{\hat{y}} = X \mathbf{w} + b $$where $\mathbf{w} \in \mathbb{R}^2$ and $b \in \mathbb{R}$ are the trainable coefficients.
To simplify the math we can include the bias as an extra coefficient in $\mathbf{w}$ by adding a column of ones in $X$, resulting in:
$$ \mathbf{\hat{y}} = X \mathbf{w}$$where $X \in \mathbb{R}^{N \times 3}$ and $\mathbf{w} \in \mathbb{R}^3$.
Let the "loss function" in this case be the Mean Squared Error (MSE), which is standard for regression problems:
$$\text{MSE} = \frac{1}{N} \sum_i^N (y_i - \hat{y}_i)^2 = \frac{1}{N} (\mathbf{y} - \mathbf{\hat{y}})^2$$We can derive the set of normal equations to solve this optimization problem analytically:
$$\begin{equation} \text{argmin}_{\mathbf{w}} \text{MSE}\\ \frac{\partial \text{MSE}}{\partial \mathbf{w}} = 0\\ \frac{\partial}{\partial \mathbf{w}} \frac{1}{N} (\mathbf{y} - (X \mathbf{w}))^2 = 0 \\ \frac{\partial}{\partial \mathbf{w}} \mathbf{y}^T\mathbf{y} - 2 \mathbf{y}^TX \mathbf{w} + (X\mathbf{w})^2 = 0 \\ -2 X^T\mathbf{y} + 2X^TX\mathbf{w} = 0 \\ -X^T\mathbf{y} + X^T X\mathbf{w} = 0 \\ X^T X\mathbf{w} = X^T\mathbf{y} \\ \mathbf{w} = (X^T X)^{-1}X^T\mathbf{y}\\ \end{equation}$$This system is called the set of normal equations, and if we plug in our 4 possible types of inputs as $X$ and $\mathbf{y}$:
- $0 \oplus 0 = 0$
- $0 \oplus 1 = 1$
- $1 \oplus 0 = 1$
- $1 \oplus 1 = 0$
and solve for $\mathbf{w}$ the result is:
- $b = 0.5$ $(= w_0)$
- $\mathbf{w} = [0, 0]^T$
As we can see, we will always get 0.5 when trying to use this linear model that best minimizes the MSE. Therefore, we need something more powerful, more non-linear, more fanciful, more doge, such as neural networks. Hence, Deep XOR.
Here the implementation in numpy:
# Normal equations, solving with the four unique examples:
X = np.array([[1, 0, 0], [1, 0, 1], [1, 1, 0], [1, 1, 1]]) # Added the bias as ones in the first column
y = np.array([0, 1, 1, 0])
b, w1, w2 = np.dot(np.linalg.inv(np.dot(X.T, X)), np.dot(X.T, y))
print("b = {}, w = [{}, {}]".format(b, w1, w2))
b = 0.5, w = [0.0, 0.0]