SYDE 556/750: Simulating Neurobiological Systems¶
Accompanying Readings: Chapter 8
DO ADMIN STUFF: NEW ASSIGNMENT, PROJECT
jupyter nbconvert --to pdf my_name.assignment1.ipynb
Dynamics¶
- Everything we've looked at so far has been feedforward
- There's some pattern of activity in one group of neurons representing $x$
- We want that to cause some pattern of activity in another group of neurons to represent $y=f(x)$
- These can be chained together to make more complex systems $z=h(f(x)+g(y))$
- What about recurrent networks?
- What happens when we connect a neural group back to itself?

Recurrent functions¶
- What if we do exactly what we've done so far in the past, but instead of connecting one group of neurons to another, we just connect it back to itself
- Instead of $y=f(x)$
- We get $x=f(x)$ (???)
- As written, this is clearly non-sensical
- For example, if we do $f(x)=x+1$ then we'd have $x=x+1$, or $x-x=1$, or $0=1$
- But don't forget about time
- What if it was $x_{t+1} = f(x_t)$
- Which makes more sense because we're talking about a real physical system
- This is a lot like a differential equation
- What would happen if we built this?
Try it out¶
- Let's try implementing this kind of circuit
- Start with $x_{t+1}=x_t+1$
%pylab inline
WARNING: pylab import has clobbered these variables: ['piecewise'] `%matplotlib` prevents importing * from pylab and numpy
import nengo
model = nengo.Network()
with model:
ensA = nengo.Ensemble(100, dimensions=1)
def feedback(x):
return x+1
conn = nengo.Connection(ensA, ensA, function=feedback, synapse = 0.1)
ensA_p = nengo.Probe(ensA, synapse=.01)
sim = nengo.Simulator(model)
sim.run(.5)
plot(sim.trange(), sim.data[ensA_p])
ylim(-1.5,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
That sort of makes sense
- $x$ increases quickly, then hits an upper bound
How quickly?
- What parameters of the system affect this?
What are the precise dynamics?
What about $f(x)=-x$?
with model:
def feedback(x):
return -x
conn.function = feedback
sim = nengo.Simulator(model)
sim.run(.5)
plot(sim.trange(), sim.data[ensA_p])
ylim(-1.5,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
- That also makes sense. What if we nudge it away from zero?
from nengo.utils.functions import piecewise
with model:
stim = nengo.Node(piecewise({0:1, .2:-1, .4:0}))
nengo.Connection(stim, ensA)
sim = nengo.Simulator(model)
sim.run(.6)
plot(sim.trange(), sim.data[ensA_p])
ylim(-1.5,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
With an input of 1, $x=0.5$
With an input of -1, $x=-0.5$
With an input of 0, it goes back to $x=0$
Does this make sense?
- Why / why not?
- And why that particular timing/curvature?
What about $f(x)=x^2$?
with model:
stim.output = piecewise({.1:.2, .2:.4, .5:0})
def feedback(x):
return x*x
conn.function = feedback
sim = nengo.Simulator(model)
sim.run(.6)
plot(sim.trange(), sim.data[ensA_p])
ylim(-1.5,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
- Well that's weird
- Stable at $x=0$ with no input
- Stable at .2
- Unstable at .4, shoots up high
- Something very strange happens around $x=1$ when the input is turned off (why decay if $f(x) = x^2$?)
- Why is this happening?
Making sense of dynamics¶
- Let's go back to something simple
- Just a single feed-forward neural population
- Encode $x$ into current, compute spikes, decode filtered spikes into $\hat{x}$
- Instead of a constant input, let's change the input
- Change it suddenly from zero to one to get a sense of what's happening with changes
import nengo
from nengo.utils.functions import piecewise
model = nengo.Network(seed=4)
with model:
stim = nengo.Node(piecewise({.3:1}))
ensA = nengo.Ensemble(100, dimensions=1)
def feedback(x):
return x
nengo.Connection(stim, ensA)
#conn = nengo.Connection(ensA, ensA, function=feedback)
stim_p = nengo.Probe(stim)
ensA_p = nengo.Probe(ensA, synapse=0.1)
sim = nengo.Simulator(model)
sim.run(1)
plot(sim.trange(), sim.data[ensA_p], label="$\hat{x}$")
plot(sim.trange(), sim.data[stim_p], label="$x$")
legend()
ylim(-.2,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
- This was supposed to compute $f(x)=x$
- For a constant input, that works
- But we get something else when there's a change in the input
- What is this difference?
- What affects it?
with model:
ensA_p = nengo.Probe(ensA, synapse=0.03)
sim = nengo.Simulator(model)
sim.run(1)
plot(sim.trange(), sim.data[ensA_p], label="$\hat{x}$")
plot(sim.trange(), sim.data[stim_p], label="$x$")
legend()
ylim(-.2,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
- The time constant of the post-synaptic filter
- We're not getting $f(x)=x$
- Instead we're getting $f(x(t))=x(t)*h(t)$
tau = 0.03
with model:
ensA_p = nengo.Probe(ensA, synapse=tau)
sim = nengo.Simulator(model)
sim.run(1)
stim_filt = nengo.Lowpass(tau).filt(sim.data[stim_p], dt=sim.dt)
plot(sim.trange(), sim.data[ensA_p], label="$\hat{x}$")
plot(sim.trange(), sim.data[stim_p], label="$x$")
plot(sim.trange(), stim_filt, label="$h(t)*x(t)$")
legend()
ylim(-.2,1.5);
Building finished in 0:00:01. Simulating finished in 0:00:01.
- So there are dynamics and filtering going on, since there is always a synaptic filter on a connection
- why isn't it exactly the same?
- Recurrent connections are dynamic as well (i.e. passing past information to future state of the population)
- Let's take a look more carefully
Recurrent connections¶
So a connection actually approximates $f(x(t))*h(t)$
So what does a recurrent connection do?
- Also $x(t) = f(x(t))*h(t)$
where $$
h(t) = \begin{cases} e^{-t/\tau} &\mbox{if } t > 0 \\ 0 &\mbox{otherwise} \end{cases} $$
- How can we work with this?
- General rule of thumb: convolutions are annoying, so let's get rid of them
- We could do a Fourier transform
- $X(\omega)=F(\omega)H(\omega)$
- But, since we are studying the response of a system (rather than a continuous signal), there's a more general and appropriate transform that makes life even easier:
- Laplace transform (it is more general because $s = a + j\omega$)
- The Laplace transform of our equations are:
- $X(s)=F(s)H(s)$
- $H(s)={1 \over {1+s\tau}}$
- Rearranging:
$X(s)=F(s){1 \over {1+s\tau}}$
$X(s)(1+s\tau) = F(s)$
$X(s) + X(s)s\tau = F(s)$
$sX(s) = {1 \over \tau} (F(s)-X(s))$
- Convert back into the time domain (inverse Laplace):
${dx \over dt} = {1 \over \tau} (f(x(t))-x(t))$
Dynamics¶
This says that if we introduce a recurrent connection, we end up implementing a differential equation
So what happened with $f(x)=x+1$?
- $\dot{x} = {1 \over \tau} (x+1-x)$
- $\dot{x} = {1 \over \tau}$
What about $f(x)=-x$?
- $\dot{x} = {1 \over \tau} (-x-x)$
- $\dot{x} = {-2x \over \tau}$
- Consistent with figures above, so at inputs of $\pm 1$ get to $0 = 2x\pm 1$, $x=\pm .5$
And $f(x)=x^2$?
- $\dot{x} = {1 \over \tau} (x^2-x)$
- Consistent with figure, at input of .2, $0=x^2-x+.2=(x-.7)(x-.2)$, for input of .4 you get imaginary solutions.
- For 0 input, x = 0,1 ... what if we get it over 1 before turning off input?
Synthesis¶
- What if there's some differential equation we really want to implement?
- We want $\dot{x} = f(x)$
- So we do a recurrent connection of $f'(x)=\tau f(x)+x$
- The resulting model will end up implementing $\dot{x} = {1 \over \tau} (\tau f(x)+x-x)=f(x)$
Inputs¶
What happens if there's an input as well?
- We'll call the input $u$ from another population, and it is also computing some function $g(u)$
- $x(t) = f(x(t))*h(t)+g(u(t))*h(t)$
Follow the same derivation steps
- $\dot{x} = {1 \over \tau} (f(x)-x + g(u))$
So if you have some input that you want added to $\dot{x}$, you need to scale it by $\tau$
This lets us do any differential equation of the form $\dot{x}=f(x)+g(u)$
A derivation¶
Linear systems¶
- The book shows that we can implement any equation of the form
$\dot{x}(t) = A x(t) + B u(t)$
- Where $A$ and $x$ are a matrix and vector -- giving a standard control theoretic structure
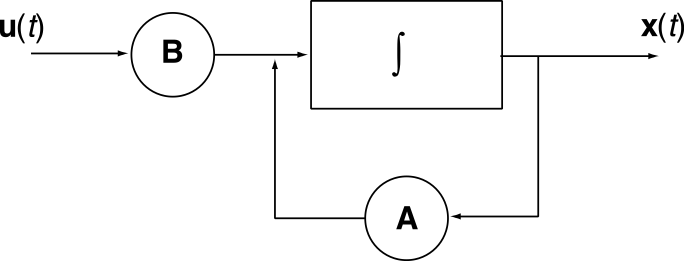 - Our goal is to convert this to a structure which has $h(t)$ as the transfer function instead of the standard $\int$
- Our goal is to convert this to a structure which has $h(t)$ as the transfer function instead of the standard $\int$
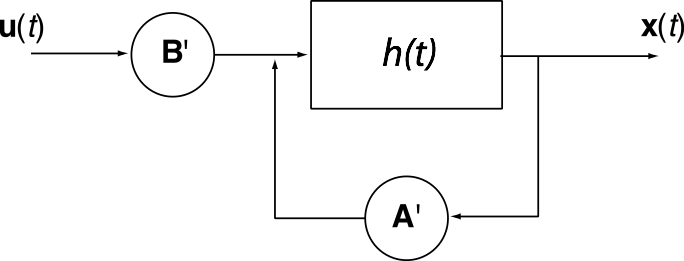
- Using Laplace on the standard form gives:
$sX(s) = A X(s) + B U(s)$
- Laplace on the 'neural control' form gives (as before where $F(s) = A'X(s) + B'U(s)$):
$X(s) = {1 \over {1 + s\tau}} (A'X(s) + B'U(s))$
$X(s) + \tau sX(s) = (A'X(s) + B'U(s))$
$sX(s) = {1 \over \tau} (A'X(s) + B'U(s) - X(s))$
$sX(s) = {1 \over \tau} ((A' - 1) X(s) + B'U(s))$
- Making the 'standard' and 'neural' equations equal to one another, we find that for any system with a given A and B, the A' and B' of the equivalent neural system are given by:
$A' = \tau A + I$ and
$B' = \tau B$
where $I$ is the identity matrix
This is nice because lots of engineers think of the systems they build in these terms (i.e. as linear control systems).
Nonlinear systems¶
- In fact, these same steps can be taken to account for nonlinear control systems as well:
$\dot{x}(t) = f(x(t),u(t),t)$
- For a neural system with transfer function $h(t)$:
$X(s) = H(s)F'(X(s),U(s),s)$
$X(s) = {1 \over {1 + s\tau}} F'(X(s),U(s),s)$
$sX(s) = {1 \over \tau} (F'(X(s),U(s),s) - X(s))$
- This gives the general result (slightly more general than what we saw earlier):
$F'(X(s),U(s),s) = \tau(F(X(s),U(s),s)) + X(s)$
- It's a linear system, so, to get it in the standard control form $\dot{x}=Ax+Bu$ we have:
- $A=0$
- $B=1$
- So that means we need $A'=\tau 0 + I = 1$ and $B'=\tau 1 = \tau$
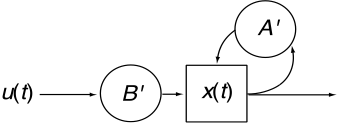
import nengo
from nengo.utils.functions import piecewise
from nengo.utils.ensemble import tuning_curves
tau = 0.01
model = nengo.Network('Eye control', seed=8)
with model:
stim = nengo.Node(piecewise({.3:1, .6:0 }))
velocity = nengo.Ensemble(100, dimensions=1)
position = nengo.Ensemble(200, dimensions=1)
def feedback(x):
return 1*x
conn = nengo.Connection(stim, velocity)
conn = nengo.Connection(velocity, position, transform=tau, synapse=tau)
conn = nengo.Connection(position, position, function=feedback, synapse=tau)
stim_p = nengo.Probe(stim)
position_p = nengo.Probe(position, synapse=.01)
velocity_p = nengo.Probe(velocity, synapse=.01)
sim = nengo.Simulator(model)
sim.run(1)
x, A = tuning_curves(position, sim)
#plot(x,A)
plot(sim.trange(), sim.data[stim_p], label = "stim")
plot(sim.trange(), sim.data[position_p], label = "position")
plot(sim.trange(), sim.data[velocity_p], label = "velocity")
legend(loc="best");
Building finished in 0:00:01. Simulating finished in 0:00:01.
- That's pretty good... the area under the input is about equal to the magnitude of the output.
- But, in order to be a perfect integrator, we'd need exactly $x=1\times x$
- We won't get exactly that
- Neural implementations are always approximations
- Two forms of error:
- $E_{distortion}$, the decoding error
- $E_{noise}$, the random noise error
- What will they do?
import nengo
from nengo.dists import Uniform
from nengo.utils.ensemble import tuning_curves
model = nengo.Network(label='Neurons')
with model:
neurons = nengo.Ensemble(200, dimensions=1, max_rates=Uniform(100,200))
connection = nengo.Connection(neurons, neurons)
sim = nengo.Simulator(model)
d = sim.data[connection].weights.T
x, A = tuning_curves(neurons, sim)
xhat = numpy.dot(A, d)
plot(x, xhat-x)
axhline(0, color='k')
xlabel('$x$')
ylabel('$\hat{x}-x$');
Building finished in 0:00:01.
- So we can think of the distortion error as introducing a bunch of local attractors into the representation
- Any 'downward' x-crossing will be a stable point ('upwards' is unstable).
- There will be a tendency to drift towards one of these even if the input is zero.
Noise error¶
- What will random noise do?
- Push the representation back and forth
- What if it is small?
- What if it is large?
- What will changing the post-synaptic time constant $\tau$ do?
- How does that interact with noise?
- But real eyes aren't perfect integrators
- If you get someone to look at someting, then turn off the lights but tell them to keep looking in the same direction, their eye will drift back to centre (with about 70s time constant)
- How do we implement that?
$\dot{x}=-{1 \over \tau_c}x + v$
$\tau_c$ is the time constant of that return to centre
$A'=\tau {-1 \over \tau_c}+1$
$B' = \tau$
import nengo
from nengo.utils.functions import piecewise
tau = 0.1
tau_c = 2.0
model = nengo.Network('Eye control', seed=5)
with model:
stim = nengo.Node(piecewise({.3:1, .6:0 }))
velocity = nengo.Ensemble(100, dimensions=1)
position = nengo.Ensemble(200, dimensions=1)
def feedback(x):
return (-tau/tau_c + 1)*x
conn = nengo.Connection(stim, velocity)
conn = nengo.Connection(velocity, position, transform=tau, synapse=tau)
conn = nengo.Connection(position, position, function=feedback, synapse=tau)
stim_p = nengo.Probe(stim)
position_p = nengo.Probe(position, synapse=.01)
velocity_p = nengo.Probe(velocity, synapse=.01)
sim = nengo.Simulator(model)
sim.run(5)
plot(sim.trange(), sim.data[stim_p], label = "stim")
plot(sim.trange(), sim.data[position_p], label = "position")
plot(sim.trange(), sim.data[velocity_p], label = "velocity")
legend(loc="best");
Building finished in 0:00:01. Simulating finished in 0:00:02.
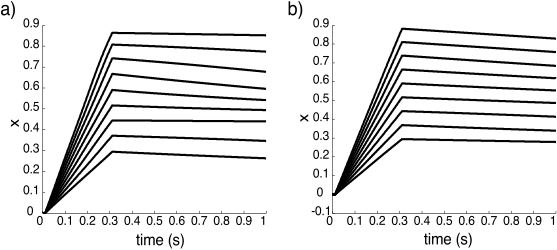
- That also looks right. Note that as $\tau_c \rightarrow \infty$ this will approach the integrator.
- Humans (a) and Goldfish (b)
- Humans have more neurons doing this than goldfish (~1000 vs ~40)
- They also have slower decay (70 s vs. 10 s).
- Why do these fit together?
Controlled Integrator¶
- What if we want an integrator where we can adjust the decay on-the-fly?
- Separate input telling us what the decay constant $d$ should be
$\dot{x} = -d x + v$
So there are two inputs: $v$ and $d$
This is no longer in the standard $Ax + Bu$ form. Sort of...
- Let $A = -d(t)$, so it's not a matrix
- But it is of the more general form: ${dx \over dt}=f(x)+g(u)$
We need to compute a nonlinear function of an input ($d$) and the state variable ($x$)
How can we do this?
- Going to 2D so we can compute the nonlinear function
- Let's have the state variable be $[x, d]$

import nengo
from nengo.utils.functions import piecewise
tau = 0.1
model = nengo.Network('Controlled integrator', seed=1)
with model:
vel = nengo.Node(piecewise({.2:1.5, .5:0 }))
dec = nengo.Node(piecewise({.7:.2, .9:0 }))
velocity = nengo.Ensemble(100, dimensions=1)
decay = nengo.Ensemble(100, dimensions=1)
position = nengo.Ensemble(400, dimensions=2)
def feedback(x):
return -x[1]*x[0]+x[0], 0
conn = nengo.Connection(vel, velocity)
conn = nengo.Connection(dec, decay)
conn = nengo.Connection(velocity, position[0], transform=tau, synapse=tau)
conn = nengo.Connection(decay, position[1], synapse=0.01)
conn = nengo.Connection(position, position, function=feedback, synapse=tau)
position_p = nengo.Probe(position, synapse=.01)
velocity_p = nengo.Probe(velocity, synapse=.01)
decay_p = nengo.Probe(decay, synapse=.01)
sim = nengo.Simulator(model)
sim.run(1)
plot(sim.trange(), sim.data[decay_p])
lineObjects = plot(sim.trange(), sim.data[position_p])
plot(sim.trange(), sim.data[velocity_p])
legend(('decay','position','decay','velocity'),loc="best");
from nengo_gui.ipython import IPythonViz
IPythonViz(model, "configs/controlled_integrator.py.cfg")
Other fun functions¶
- Oscillator
- $F = -kx = m \ddot{x}$ let $\omega = \sqrt{\frac{k}{m}}$
- $\frac{d}{dt} \begin{bmatrix}
\omega x \ \dot{x} \end{bmatrix} = \begin{bmatrix} 0 & \omega \\ -\omega & 0 \end{bmatrix}$ - $\dot{x}=[x_1, -x_0]$
import nengo
model = nengo.Network('Oscillator')
freq = 1
with model:
stim = nengo.Node(lambda t: [.5,.5] if t<.02 else [0,0])
osc = nengo.Ensemble(200, dimensions=2)
def feedback(x):
return x[0]+freq*x[1], -freq*x[0]+x[1]
nengo.Connection(osc, osc, function=feedback, synapse=.01)
nengo.Connection(stim, osc)
osc_p = nengo.Probe(osc, synapse=.01)
sim = nengo.Simulator(model)
sim.run(.5)
figure(figsize=(12,4))
subplot(1,2,1)
plot(sim.trange(), sim.data[osc_p]);
xlabel('Time (s)')
ylabel('State value')
subplot(1,2,2)
plot(sim.data[osc_p][:,0],sim.data[osc_p][:,1])
xlabel('$x_0$')
ylabel('$x_1$');
from nengo_gui.ipython import IPythonViz
IPythonViz(model, "configs/oscillator.py.cfg")
Lorenz Attractor (a chaotic attractor)
- $\dot{x}=[10x_1-10x_0, -x_0 x_2-x_1, x_0 x_1 - {8 \over 3}(x_2+28)-28]$
import nengo
model = nengo.Network('Lorenz Attractor', seed=3)
tau = 0.1
sigma = 10
beta = 8.0/3
rho = 28
def feedback(x):
dx0 = -sigma * x[0] + sigma * x[1]
dx1 = -x[0] * x[2] - x[1]
dx2 = x[0] * x[1] - beta * (x[2] + rho) - rho
return [dx0 * tau + x[0],
dx1 * tau + x[1],
dx2 * tau + x[2]]
with model:
lorenz = nengo.Ensemble(2000, dimensions=3, radius=60)
nengo.Connection(lorenz, lorenz, function=feedback, synapse=tau)
lorenz_p = nengo.Probe(lorenz, synapse=tau)
sim = nengo.Simulator(model)
sim.run(14)
figure(figsize=(12,4))
subplot(1,2,1)
plot(sim.trange(), sim.data[lorenz_p]);
xlabel('Time (s)')
ylabel('State value')
subplot(1,2,2)
plot(sim.data[lorenz_p][:,0],sim.data[lorenz_p][:,1])
xlabel('$x_0$')
ylabel('$x_1$');
from nengo_gui.ipython import IPythonViz
IPythonViz(model, "configs/lorenz.py.cfg")
- Note: This is not the original Lorenz attractor.
- The original is $\dot{x}=[10x_1-10x_0, x_0 (28-x_2)-x_1, x_0 x_1 - {8 \over 3}(x_2)]$
- Why change it to $\dot{x}=[10x_1-10x_0, -x_0 x_2-x_1, x_0 x_1 - {8 \over 3}(x_2+28)-28]$?
- What's being changed here?
Oscillators with different paths¶
- Since we can implement any function, we're not limited to linear oscillators
- What about a "square" oscillator?
- Instead of the value going in a circle, it traces out a square
import nengo
model = nengo.Network('Square Oscillator')
tau = 0.02
r=4
def feedback(x):
if abs(x[1])>abs(x[0]):
if x[1]>0: dx=[r, 0]
else: dx=[-r, 0]
else:
if x[0]>0: dx=[0, -r]
else: dx=[0, r]
return [tau*dx[0]+x[0], tau*dx[1]+x[1]]
with model:
stim = nengo.Node(lambda t: [.5,.5] if t<.02 else [0,0])
square_osc = nengo.Ensemble(1000, dimensions=2)
nengo.Connection(square_osc, square_osc, function=feedback, synapse=tau)
nengo.Connection(stim, square_osc)
square_osc_p = nengo.Probe(square_osc, synapse=tau)
sim = nengo.Simulator(model)
sim.run(2)
figure(figsize=(12,4))
subplot(1,2,1)
plot(sim.trange(), sim.data[square_osc_p]);
xlabel('Time (s)')
ylabel('State value')
subplot(1,2,2)
plot(sim.data[square_osc_p][:,0],sim.data[square_osc_p][:,1])
xlabel('$x_0$')
ylabel('$x_1$');
- Does this do what you expect?
- How is it affected by:
- Number of neurons?
- Post-synaptic time constant?
- Decoding filter time constant?
- Speed of oscillation (
r)?
- What about this shape?
import nengo
model = nengo.Network('Heart Oscillator')
tau = 0.02
r=4
def feedback(x):
return [-tau*r*x[1]+x[0], tau*r*x[0]+x[1]]
def heart_shape(x):
theta = np.arctan2(x[1], x[0])
r = 2 - 2 * np.sin(theta) + np.sin(theta)*np.sqrt(np.abs(np.cos(theta)))/(np.sin(theta)+1.4)
return -r*np.cos(theta), r*np.sin(theta)
with model:
stim = nengo.Node(lambda t: [.5,.5] if t<.02 else [0,0])
heart_osc = nengo.Ensemble(1000, dimensions=2)
heart = nengo.Ensemble(100, dimensions=2, radius=4)
nengo.Connection(stim, heart_osc)
nengo.Connection(heart_osc, heart_osc, function=feedback, synapse=tau)
nengo.Connection(heart_osc, heart, function=heart_shape, synapse=tau)
heart_p = nengo.Probe(heart, synapse=tau)
sim = nengo.Simulator(model)
sim.run(4)
figure(figsize=(12,4))
subplot(1,2,1)
plot(sim.trange(), sim.data[heart_p]);
xlabel('Time (s)')
ylabel('State value')
subplot(1,2,2)
plot(sim.data[heart_p][:,0],sim.data[heart_p][:,1])
xlabel('$x_0$')
ylabel('$x_1$');
- We are doing things differently here
- The actual $x$ value is a normal circle oscillator
- The heart shape is a function of $x$
- But that's just a different decoder
- Would it be possible to do an oscillator where $x$ followed this shape?
- How could we tell them apart in terms of neural behaviour?
Controlled Oscillator¶
Change the frequency of the oscillator on-the-fly
$\dot{x}=[x_1 x_2, -x_0 x_2]$
import nengo
from nengo.utils.functions import piecewise
model = nengo.Network('Controlled Oscillator')
tau = 0.1
freq = 20
def feedback(x):
return x[1]*x[2]*freq*tau+1.1*x[0], -x[0]*x[2]*freq*tau+1.1*x[1], 0
with model:
stim = nengo.Node(lambda t: [20,20] if t<.02 else [0,0])
freq_ctrl = nengo.Node(piecewise({0:1, 2:.5, 6:-1}))
ctrl_osc = nengo.Ensemble(500, dimensions=3)
nengo.Connection(ctrl_osc, ctrl_osc, function=feedback, synapse=tau)
nengo.Connection(stim, ctrl_osc[0:2])
nengo.Connection(freq_ctrl, ctrl_osc[2])
ctrl_osc_p = nengo.Probe(ctrl_osc, synapse=0.01)
sim = nengo.Simulator(model)
sim.run(8)
figure(figsize=(12,4))
subplot(1,2,1)
plot(sim.trange(), sim.data[ctrl_osc_p]);
xlabel('Time (s)')
ylabel('State value')
subplot(1,2,2)
plot(sim.data[ctrl_osc_p][:,0],sim.data[ctrl_osc_p][:,1])
xlabel('$x_0$')
ylabel('$x_1$');
from nengo_gui.ipython import IPythonViz
IPythonViz(model, "configs/controlled_oscillator.py.cfg")
