Update 2014-10-15
Once again my answer is too complicated. Regularized logistic regression is a similar model which gives pretty much the same answer. Update discussion.
Intro¶
The typical approach to Bayesian AB testing doesn't really allow for prior knowledge on the scale of the change in conversion rate. Sometimes you know that a change will probably have only a small effect. I propose a slightly different approach that explicitly models knowledge about the expected effect size.
The usual way of thinking about it¶
We have two different versions of a website, A and B, and we wish to estimate their true conversion rates $p_A$ and $p_B$. (Or more likely we want an estimate of the difference or ratio of the conversion rates, with some notion of the uncertainty around that estimate.) We observe a number of visits, some of which convert, to each version of the site. Call these $obs_A$ and $obs_B$. We also have some prior knowledge of the possible values for $p_A$ and $p_B$ which we model as beta distributions $B_A$ and $B_B$. A typical choice for these is the flat, uniform prior for each: $B(1,1)$.
So the data story goes like this for each variation:
- Select the conversion rate $p$, where $p$ is beta distributed according to the prior $B$.
- Observe a number of visits which are Bernoulli distributed with rate $p$.
A problem with this story¶
Often the differences between A and B are small, e.g. rephrasing the call to action on a button. So you have prior knowledge that the difference in conversion rates $p_A$ and $p_B$ is probably small. The above story doesn't really allow you to use that knowledge. The problem is worse the flatter your priors $B_A$ and $B_B$ are. In the case of a uniform prior for both, we're saying that $p_A, p_B = 0\%, 100\%$ is equally likely to $p_A, p_B = 25\%, 25\%$, which is crazy for a small change.
A better data generation story¶
I use an alternative parameterization of the beta distribution, based on the mean $\mu = \frac{\alpha}{\alpha+\beta}$ and "sample size" or spread $\tau = \alpha + \beta$.
Rather than using a fixed beta prior for A and B, we allow it to vary according to our prior knowledge. The mean $\mu$ varies according to historical data, much like in the usual approach. Denote the varying beta prior $B_{\mu}$ to indicate it's dependence on $\mu$. Fix the spread $\tau$ to a value which is consistent with our beliefs about the possible effect size. $p_A$ and $p_B$ are then drawn from this beta distribution.
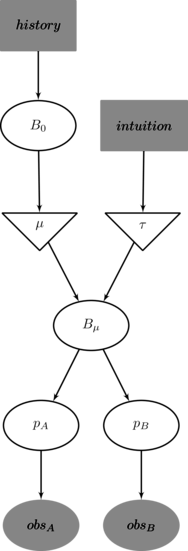
The story looks like this:
- Based on historical data, select a beta distribution $B_0$
- Draw a $\mu$ from $B_0$
- Based on intuition/experience, choose a spread parameter $\tau$
- We now have a beta distribution $B_{\mu}$
- Select $p_A$ and $p_B$ from $B_{\mu}$
- Observe visits that are Bernoulli distributed according to $p_A$ and $p_B$
In picture form:
Tuning $\tau$¶
The step for coming up with $\tau$ sounds a bit magical in the above description, so let's be more concrete. Suppose that from our historical data, the mean conversion rate for situations similar to our current experiment is 10%, so $\mu=.1$. Setting $\tau=1500$ then produces a distribution of the conversion rate difference shown below. Increasing $\tau$ narrows the distribution. Use a bit of guess and check to come up with something reasonable here.
import numpy as np
from scipy.stats import beta as beta_dist
%matplotlib inline
mu = .10
tau = 1500
alpha, beta = mu*tau, (1-mu)*tau
pA = beta_dist.rvs(alpha,beta,size=10000)
pB = beta_dist.rvs(alpha,beta,size=10000)
diff = Series(pA-pB)
diff.hist(bins=np.arange(-.05,.06,.01), histtype='stepfilled')
print(diff.describe())
count 10000.000000 mean 0.000137 std 0.010988 min -0.042673 25% -0.007296 50% 0.000271 75% 0.007532 max 0.037420 dtype: float64
Example¶
In the example below, it's early in the AB test and we only have a few thousand sessions. But the results look very promising, almost a 15% lift in the empirical conversion rate. But how realistic is that, if it was only a small change to the website? Should we stop the test and call it a win?
I take a look at the estimated percentage improvement in conversion rate with the usual method versus the new method. For the usual method, I try it with a flat prior $B(1,1)$ as well as the very informative prior $B(30, 270)$.
The new method gives a much more modest estimate of the improvement.
successesA = 300
successesB = 350
failuresA = 3000
failuresB = 3000
pA, pB = successesA/(successesA+failuresA), successesB/(successesB+failuresB)
pA, pB, (pB-pA)/pA
(0.09090909090909091, 0.1044776119402985, 0.1492537313432835)
def usual_method(alpha=1, beta=1):
pA = beta_dist.rvs(alpha+successesA,beta+failuresA,size=10000)
pB = beta_dist.rvs(alpha+successesB,beta+failuresB,size=10000)
lift = Series((pB-pA)/pA)
return lift
def new_method(alpha0=3, beta0=27, tau=1500):
mu_samples = beta_dist.rvs(alpha0, beta0, size=10000)
def compute_p(mu):
alpha, beta = mu*tau, (1-mu)*tau
pA = beta_dist.rvs(alpha+successesA,beta+failuresA)
pB = beta_dist.rvs(alpha+successesB,beta+failuresB)
return pA, pB
p = np.array([compute_p(mu) for mu in mu_samples])
pA, pB = p[:, 0], p[:, 1]
lift = Series((pB-pA)/pA)
return lift
lift0 = usual_method()
lift1 = usual_method(30, 270)
lift2 = new_method()
df = DataFrame({'Flat prior': lift0, 'Very informative prior': lift1, 'New method': lift2})
df = pd.melt(df)
If we're using a simple decision rule like "stop the test if one variation has a 95% or greater of being the best" then the usual method would stop here, but the new method would want to gather more data:
(lift0<0).mean(), (lift1<0).mean(), (lift2<0).mean()
(0.031800000000000002, 0.035200000000000002, 0.059999999999999998)
Even using an unrealistically informative prior doesn't shift our estimated CVR lift too much. But the new method does.
%load_ext rmagic
%%R -i df -w 900
library(ggplot2)
p <- ggplot(df, aes(x=value, color=variable)) + geom_density()
p + xlab('Estimated conversion rate lift') + xlim(-.1, .4)