Content under Creative Commons Attribution license CC-BY 4.0, code under MIT license (c)2014 L.A. Barba, C.D. Cooper, G.F. Forsyth.¶
Riding the wave¶
We've reached the third lesson of the module Riding the wave: Convection problems, where we explore the numerical solution of conservation laws. We learned in the first lesson how to think about conservation laws, starting with the most intuitive case: that of conservation of mass. But there are many physical quantities that can be conserved: energy, for example. Or cars on a road.
Developing a conservation law for traffic in a one-lane roadway is fun, because we can relate to the insights it gives. We've all experienced traffic slowing down to a crawl when the density of cars gets very high, and stepping on the accelerator pedal with glee when there are no cars on the road!
In the previous two lessons, we developed a traffic-flow model and explored different choices of numerical scheme. Not everything worked as you expected, and by now you might be realizing how some restrictions come about from the numerical methods themselves, while others still are imposed by the models we use. This lesson will develop a better traffic model, and also show you some impressive SymPy kung-fu.
Traffic flow, revisited¶
A better flux model¶
Like you saw in the first lesson, cars obey a typical conservation law,
$$ \begin{equation} \frac{\partial \rho}{\partial t} + \frac{\partial F}{\partial x} = 0 \end{equation} $$where $F$ is the flux, $F=\rho u$—flux equals density times velocity. From our experience on the road, we know that the traffic speed is a function of traffic density, and we proposed as a first approximation a linear relation between the two. Thus,
$$ \begin{equation} F(\rho) = \rho \, u_{max}\left(1 - \frac{\rho}{\rho_{max}} \right) \end{equation} $$This flux model meets the two requirements, based on a qualitative view of traffic flow, that:
- $u \rightarrow u_{max}$ and $F\rightarrow 0$ when $\rho \rightarrow 0$.
- $u \rightarrow 0$ as $\rho \rightarrow \rho_{max}$
However, it leads to some unrealistic or at least improbable results. For example, note that if the traffic speed is a linear function of density, the flux function will be quadratic (see Figure 1). In this case, the maximum flux will occur when $\rho^{\star} = \rho_{max}/2$, corresponding to a traffic speed $u_{max}/2$.
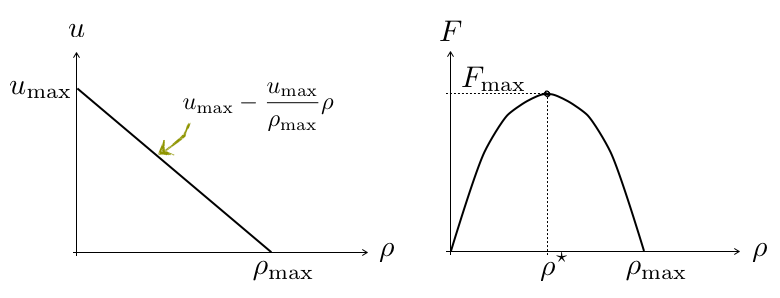
Figure 1. Traffic speed (left) and flux (right) vs. density.¶
A good question to ask here is: should the maximum flux on a given stretch of road have a strict dependence on the maximum speed that the roadway allows, be it by physical restrictions or posted speed limits? In other words, do we really expect the maximum flux to increase if we allow arbitrarily high speeds?
Probably not. But there should be some ideal traffic speed, $u^{\star}$, corresponding to an ideal traffic density, $\rho^{\star}$, resulting in the maximum traffic flux:
$$ \begin{equation} F_{\rm max} = \rho^{\star}u^{\star} \end{equation} $$Let us improve the initial flux model by taking this observation into account. One thing that we can try is to introduce a flux model that is cubic in $\rho$ instead of quadratic:
$$ \begin{equation} F(\rho) = u_{\rm max}\rho (1 - A\rho - B \rho^2) \end{equation} $$This new model still meets the first criterion listed above: $F\rightarrow 0$ when $\rho \rightarrow 0$. Moreover, we impose the following conditions:
- When $\rho = \rho_{\rm max}$ traffic flux goes to zero:
- Based on eq. (3), maximum flux occurs when $\rho = \rho^{\star}$ and $F'(\rho^{\star}) = 0$:
- $u^{\star}$ is obtained when $\rho = \rho^{\star}$:
We have three equations and four unknowns $A,B,\rho^{\star}, u^{\star}$. However, in practice, the ideal traffic speed could be obtained for a given road by observations. Similarly to $u_{max}$ and $\rho_{max}$ it will therefore be taken as a parameter.
Solving the new flux equation¶
Equations $(5)$, $(6)$, and $(7)$ are not incredibly difficult to solve with pen and paper. Instead of following that route, we can use SymPy, the symbolic mathematics library of Python. You used SymPy already in the Burgers' equation lesson of Module 2, "Space & Time", and you will learn some new functionalities here.
We begin by importing SymPy, initializing $\LaTeX$ printing and defining a set of symbolic variables that we'll use in the calculations. Remember: variables are not defined automatically, you have to tell SymPy that a name will correspond to a symbolic variable by using the keyword symbols. This behavior is different from many other symbolic math systems that implicitly construct symbols for you, so you may be perplexed if you've used these other sytems before. The reason for this behavior in SymPy is that the system is fully built on Python, a general-purpose language that needs you to define all objects before using them.
import sympy
sympy.init_printing()
(u_max, u_star, rho_max,
rho_star, A, B) = sympy.symbols('u_max u_star rho_max rho_star A B')
Notice that we used the special character _ (the under-dash) to create a symbol with a subscript. Here, for example, we've created the symbols $u_{max}$ and $u_{star}$, representing $u_{\rm max}$ and $u^{\star}$ ($u$-star) in the equations, and assigned them to the variable names u_max and u_star. SymPy also allows you to create symbols with a superscript by means of the special character ^. Be careful, though: SymPy is built on Python, so you denote an exponent in an expression by ** (this may also be different from other symbolic math systems that you have used in the past).
Next, use sympy.Eq() to define the three equations—corresponding to Equations $(5)$, $(6)$ and $(7)$, above—in terms of symbolic variables. The function sympy.Eq() creates an equality between two SymPy objects, passed as arguments separated by a comma. We need to remember that the equal sign in Python is used for variable assignment, and for that reason it cannot be used to build a symbolic equation with SymPy. That is why we need sympy.Eq() to create symbolic equalities. But the equal sign is used to assign an equation to a name: here, eq1, eq2, eq3 are names for the symbolic equalities we create with sympy.Eq().
eq1 = sympy.Eq(0, u_max * rho_max * (1 - A * rho_max - B * rho_max**2))
eq2 = sympy.Eq(0, u_max * (1 - 2 * A * rho_star - 3 * B * rho_star**2))
eq3 = sympy.Eq(u_star, u_max * (1 - A * rho_star - B * rho_star**2))
Check this out: you can display these equations in pretty typeset mathematics just by executing their name in a code cell:
eq1
eq2
eq3
As stressed above, we have three equations with three unknowns (assuming we have some observed value of $u_{star}$, corresponding to the ideal traffic speed)—there must be a solution!
To eliminate the term with $B$ in eq2, leaving it only in terms of $A$ and $\rho^{\star}$, we might subtract 3*eq3. But this will not work in SymPy if you attempt equation subtraction using the equation names. Just like we couldn't use the equal sign (which in Python means assignment) to create a symbolic equality (needing sympy.Eq instead), we can't use mathematical operators directly on the SymPy equations, because they are really equalities. What does it mean to subtract two equalities? It doesn't make sense. Try it ...
eq2 - 3 * eq3
See? SymPy just printed out what you suggested but it did not manipulate algebraically the left and right sides of eq2 like we were aiming for. What we can do is create a new equation, perform the left-hand side (LHS) and right-hand side (RHS) operations separately and then recombine them into our desired result. For this, it is helpful to know that there are built-in properties of a SymPy equality for the left-hand side and the right-hand side of the equality. Check it out:
eq4 = sympy.Eq(eq2.lhs - 3 * eq3.lhs, eq2.rhs - 3 * eq3.rhs)
eq4
That still needs a little work. SymPy offers several methods to help reduce expressions. You can use simplify() to attempt to make the expression "simpler," but you can imagine that the quality of an expression being simple is not well defined. One may expect the simpler expression to be shorter, maybe; but not always. The SymPy simplify() function applies several strategies, heuristically, to give you an equivalent reduced expression. But some expressions are uncooperative and simplify() gives up, returning the argument unchanged. Let's see what it can do with our expression eq4.
eq4.simplify()
That is actually a useful result. We see that eq4 allows solving for $\rho^{\star}$ in terms of $A$, for example (remember that $u_{max}$ is known: the road's maximum velocity). Then we could try to manipulate eq1 to solve for $B$ in terms of $A$, as well, so that we can substitute back in eq2 leaving everything in terms of $A$. We can do all that without the help of simplify(), but using it interactively to reason about the long expression helped us to decide on a course of action.
Another SymPy function that can help us examine complicated expressions is expand(). Its purpose is to expand bracketed factors in expressions and group powers of symbols. Let's see what that does here. Notice first that eq4 hasn't changed; we just printed the result of applying simplify() to it.
eq4
And now we print the result of applying expand() to it.
eq4.expand()
That's very similar to our previous result, except without the bracketed factor. Simplifying an expression can be accomplished by expanding or factoring terms, or a combination of the two. Whether to simplify() or expand() depends on the situation and you just have to experiment.
We now have an idea of what to do with our three equations. We'll get expressions in terms of $A$ from eq4 and eq1 and substitute them back into eq2. For that, we can use the SymPy functions solve() and subs(), respectively. The arguments to solve() are the equality that needs to be solved, and the symbol to solve for.
Note: sympy.solve() always returns results in a list, since you often end up with multiple solutions for a given variable. These linear equations will only return one solution, so we can skip a step and ask right away for the [0]-th element of the list.
rho_sol = sympy.solve(eq4, rho_star)[0]
rho_sol
B_sol = sympy.solve(eq1, B)[0]
B_sol
The arguments to the SymPy function subs() are given as (old, new) pairs, where the "new" expression substitutes the "old" one. So here, in eq2, we substitute rho_sol in place of rho_star and we substitute B_sol in place of B.
quadA = eq2.subs([(rho_star, rho_sol), (B, B_sol)])
quadA
quadA.simplify()
It's a little bit ugly, but that is quadratic in $A$, and that means we can solve for the roots of the equation. SymPy's solve() function in this case will return a list with the two roots. They are long expressions, so let's print each root separately.
A_sol = sympy.solve(quadA, A)
A_sol[0]
A_sol[1]
Evaluating the new flux equation¶
Quadratic equations, of course, have two solutions. Here we have to select the positive root, otherwise our model would have an inconsistency. Are you able to see why? To determine its value, we need to fill in some actual numbers into the model.
Let's start with the same numerical values that we used in lesson 1 for $\rho_{\rm max}$ and $u_{\rm max}$. But we also have to supply a value for $u^{\star}$, a quantity that should be experimentally observed in a given road. We propose $u^{\star} = 0.7\, u_{\rm max}$ for this exercise. This would correspond to 84 km/h for a highway with a 120-km/h speed limit, for example.
Let's numerically evaluate the solutions for $A$ using the following values:
$$ \begin{align} \rho_{\rm max} &=10.0 \nonumber\\ u_{\rm max} &=1.0 \nonumber\\ u^{\star} &=0.7 \nonumber \end{align} $$Now evaluate the numeric result for each root of $A$ using the evalf() function, where you pass the numeric substitution as an argument. It's very cool. Let's evaluate both roots and we will pick the positive one.
Let's try the [0]-th solution for $A$, first:
A_val_0 = A_sol[0].evalf(subs={u_star: 0.7, u_max: 1.0, rho_max: 10.0})
A_val_0
Now let's try the [1]-th solution for $A$:
A_val_1 = A_sol[1].evalf(subs={u_star: 0.7, u_max: 1.0, rho_max: 10.0})
A_val_1
Because Sympy seems not to return the roots in a deterministic order and we want to use the positive root, we will automatically pick this one by using the Python built-in max function.
A_val = max(A_val_0, A_val_1)
A_val
Now, numerically evaluate $B$ in the same way using the positive root A_val:
B_val = B_sol.evalf(subs={rho_max: 10.0, A: A_val})
B_val
Turn off $\LaTeX$¶
$\LaTeX$ output is great when we're looking at algebraic expressions, but it's a little too much for simple numeric output. Let's turn it off for the rest of the exercise:
sympy.init_printing(use_latex=False)
Green light: take 2¶
Let's re-examine the green-light problem from lesson 1 but using our newly computed traffic-flux equation. We shouldn't have to change much—in fact, we can simply create a new flux function and leave the rest of the code unchanged.
There's one last bit of housekeeping to do so we don't run into trouble -- we used the variables rho_max and u_max in our SymPy code and we defined them as SymPy symbols. You can check on the status of a variable using type().
print(type(rho_max), type(u_max))
<class 'sympy.core.symbol.Symbol'> <class 'sympy.core.symbol.Symbol'>
If we try to use SymPy variables with NumPy arrays, Python is going to be very unhappy. We can re-define them as floats and avoid that messy situation.
rho_max = 10.0
u_max = 1.0
def flux(rho, u_max, A, B):
"""
Computes the traffic flux for the better model.
Parameters
----------
rho : numpy.ndarray
Traffic density along the road as a 1D array of floats.
u_max : float
Maximum speed allowed on the road.
A : float
Scaling coefficient for rho.
B : float
Scaling coefficient for rho squared.
Returns
-------
F : numpy.ndarray
The traffic flux along the road as a 1D array of floats.
"""
F = rho * u_max * (1.0 - A * rho - B * rho**2)
return F
import numpy
from matplotlib import pyplot
%matplotlib inline
# Set the font family and size to use for Matplotlib figures.
pyplot.rcParams['font.family'] = 'serif'
pyplot.rcParams['font.size'] = 16
def rho_green_light(x, rho_light):
"""
Computes the "green light" initial condition.
It consists of a shock with a linear distribution behind it.
Parameters
----------
x : numpy.ndarray
Locations on the road as a 1D array of floats.
rho_light : float
Car density at the stoplight.
Returns
-------
rho : numpy.ndarray
The initial car density along the road
as a 1D array of floats.
"""
rho = numpy.zeros_like(x)
mask = numpy.where(x < 2.0)
rho[mask] = rho_light * x[mask] / 2.0
return rho
# Set parameters.
nx = 81 # number of locations on the road
L = 4.0 # length of the road
dx = L / (nx - 1) # distance between two consecutive locations
nt = 30 # number of time steps to compute
rho_light = 5.0 # car density at the traffic light.
# Define the locations on the road.
x = numpy.linspace(0.0, L, num=nx)
# Compute the initial traffic density.
rho0 = rho_green_light(x, rho_light)
# Plot the initial car density on the road.
fig = pyplot.figure(figsize=(6.0, 4.0))
pyplot.xlabel(r'$x$')
pyplot.ylabel(r'$\rho$')
pyplot.grid()
line = pyplot.plot(x, rho0,
color='C0', linestyle='-', linewidth=2)[0]
pyplot.xlim(0.0, L)
pyplot.ylim(-0.5, 6.0)
pyplot.tight_layout();
def ftbs(rho0, nt, dt, dx, bc_value, *args):
"""
Computes the traffic density on the road
at a certain time given the initial traffic density.
Parameters
----------
rho0 : numpy.ndarray
The initial car density along the road
as a 1D array of floats.
nt : integer
The number of time steps to compute.
dt : float
The time-step size to integrate.
dx : float
The distance between two consecutive locations.
bc_value : float
The constant density at the first station.
args : list or tuple
Positional arguments to be passed to the flux function.
Returns
-------
rho_hist : list of numpy.ndarray objects
The history of the car density along the road.
"""
rho_hist = [rho0.copy()]
rho = rho0.copy()
for n in range(nt):
# Compute the flux.
F = flux(rho, *args)
# Advance in time.
rho[1:] = rho[1:] - dt / dx * (F[1:] - F[:-1])
# Set the left boundary condition.
rho[0] = bc_value
# Record the time-step solution.
rho_hist.append(rho.copy())
return rho_hist
# Set time-step size based on CFL limit.
sigma = 1.0
dt = sigma * dx / u_max # time-step size
# Compute the traffic density at all time steps.
rho_hist = ftbs(rho0, nt, dt, dx, rho0[0], u_max, A_val, B_val)
Now that we have computed the history of the car density along the road, let's create an animation to visualize the results.
from matplotlib import animation
from IPython.display import HTML
def update_plot(n, rho_hist):
"""
Update the line y-data of the Matplotlib figure.
Parameters
----------
n : integer
The time-step index.
rho_hist : list of numpy.ndarray objects
The history of the numerical solution.
"""
fig.suptitle('Time step {:0>2}'.format(n))
line.set_ydata(rho_hist[n])
# Create an animation of the traffic density.
anim = animation.FuncAnimation(fig, update_plot,
frames=nt, fargs=(rho_hist,),
interval=100)
# Display the video.
HTML(anim.to_html5_video())
That definitely looks different! Do you think this is more or less accurate than our previous model?
Dig Deeper¶
The new traffic-flux model that we developed here changes the way that traffic patterns evolve. In this lesson, we only experimented with the most basic scheme: forward-time, backward-space. Try to implement the green-light problem using one of the second-order schemes from Lesson 2.
References¶
- Neville D. Fowkes and John J. Mahony, "An Introduction to Mathematical Modelling," Wiley & Sons, 1994. Chapter 14: Traffic Flow.
The cell below loads the style of the notebook.¶
from IPython.core.display import HTML
css_file = '../../styles/numericalmoocstyle.css'
HTML(open(css_file, 'r').read())