whoami
stu
Machine Learning Engineer @Opendoor
@mstewart141
[comment]: <> (we are so hiring)
Goal: Puzzle through the gradient descent algorithm towards a working prototype for linear and logistic regression.¶
Per Wikipedia:
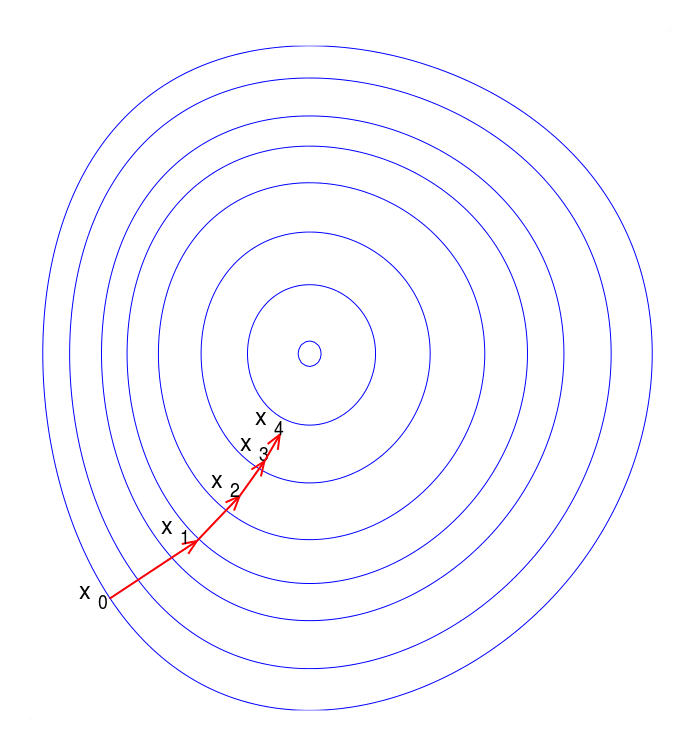
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or of the approximate gradient) of the function at the current point
Ok, but what is a gradient?¶
Per Khan Academy:
The gradient stores all the partial derivative information of a multivariable function.
The gradient is a vector-valued function: a vector of partial derivates.
 source: Wikipedia
source: Wikipedia
%matplotlib inline
import numpy as np
import sympy
from numpy.linalg import inv
from scipy.special import expit
from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.datasets import make_classification
from sympy import diff
from sympy.solvers import solve
from sympy.plotting import plot
from toolz import compose, pipe
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
np.random.seed = RS = 47
Let's look at an example¶
e = 'x*x'
plot(e);
diff(e)
2*x
gradient = np.array(['2x'])
solve(e)
[0]
You told us to "step proportional to the negative of the gradient"?¶
what if x > 0, x < 0?
Now, we'll do gradient descent live¶
Starting with linear regression¶
X, Y = make_classification(n_samples=1000, n_features=3, n_informative=3,
n_redundant=0, n_repeated=0, n_classes=2,
random_state=RS)
We need to introduce a bias term:¶
bias_column = np.ones(X.shape[0])
X = np.c_[bias_column, X]
Y = Y.ravel()
Aside: do we even need gradient descent?¶
$$X_{m \times n}, Y_{m \times 1}$$¶
Meet the 'normal' equation:¶
This gives us a way to compute our beta vector:¶
betas_normal_eq = inv(X.T @ X) @ X.T @ Y
Sanity check: Scikit-learn¶
linreg = LinearRegression(fit_intercept=False)
linreg.fit(X,Y);
betas_sklearn = linreg.coef_
betas_normal_eq
betas_sklearn
array([ 0.45801758, 0.27764882, -0.10227603, -0.04232889])
array([ 0.45801758, 0.27764882, -0.10227603, -0.04232889])
But where are the gradients???¶
Spoiler: linear and logistic regression aren't so different to optimize¶
$$\begin{equation} F(z) = z \end{equation}$$¶
$$\begin{equation} F(z) = \dfrac{1}{1+e^{-z}} \end{equation}$$¶
These two functions, let's write 'em up¶
identity = lambda z: z
sigmoid = expit
def sigmoid(z):
return 1 / (1 + np.exp(-z))
Why do these $F(z)$ equations matter? What is our hypothesis?¶
Our two hypotheses will be identical, except for the aforementioned functions!¶
Recall the normal equation?¶
hypothesis = X @ betas_sklearn
hypothesis_shape = hypothesis.shape
hypothesis_shape
(1000,)
Gradient Descent!¶
Gradient descent is a first-order iterative optimization algorithm
We must define an update step that moves us closer to the solution each iteration.
def gradient_descent(X=X, Y=Y, kind='linear', learning_rate=0.01, iterations=int(1e5)):
betas = np.zeros(X.shape[1])
assert kind in {'linear', 'logistic'}, f"Whoops! Don't support kind: {kind}."
fn = identity if kind == 'linear' else sigmoid
def update_step(betas):
hypothesis = fn(X @ betas)
loss = hypothesis - Y
gradient = X.T @ loss * (1 / X.shape[0])
return betas - learning_rate * gradient
return pipe(betas, *([update_step] * iterations))
# (tweetable version)
def gradient_descent(X=X, Y=Y, kind='linear', lr=0.01, n=int(1e5)):
return pipe(np.zeros(X.shape[1]), *([
lambda betas: betas - lr *
X.T @ (((identity if kind == 'linear' else sigmoid)(X @ betas)) - Y) * (1 / X.shape[0])
] * n))
Does it work for linear regression?¶
betas_gd = gradient_descent()
betas_gd
betas_normal_eq
betas_sklearn
array([ 0.45801758, 0.27764882, -0.10227603, -0.04232889])
array([ 0.45801758, 0.27764882, -0.10227603, -0.04232889])
array([ 0.45801758, 0.27764882, -0.10227603, -0.04232889])
Great! How about for logistic regression?¶
What saith Scikit?¶
logr = LogisticRegression(fit_intercept=False, C=1e18)
logr.fit(X,Y);
betas_logr = logr.coef_[0]
betas_gdl = gradient_descent(kind='logistic')
np.round(betas_logr, 2)
np.round(betas_gdl, 2)
array([-0.13, 3.08, -1.04, -0.41])
array([-0.13, 3.08, -1.04, -0.41])
Bold claim: we're 90% of the way to a fully formed sklearn estimator!¶
class GradientDescentClassifierRegressor:
def __init__(self, kind='linear', learning_rate=0.01, iterations=int(1e5)):
self.kind = kind
self.learning_rate = learning_rate
self.iterations = iterations
def fit(self, X, Y):
self.coef_ = gradient_descent(
X,
Y,
self.kind,
self.learning_rate,
self.iterations,
)
return self
def predict(self, X):
try:
getattr(self, 'coef_') # illustrative
fn = identity if self.kind == 'linear' else lambda arr: np.round(sigmoid(arr)).astype(int)
return fn(X @ self.coef_)
except AttributeError:
raise RuntimeError('Must fit first!!!')
gdcr = GradientDescentClassifierRegressor(kind='linear')
gdcr.fit(X,Y);
gdcr.predict(X[:10])
linreg.predict(X[:10])
array([ 0.61911337, 0.3343834 , 0.49442232, 0.5050518 , -0.20501244,
0.00771493, -0.06387987, 1.02075149, 0.51484657, 0.77049524])
array([ 0.61911337, 0.3343834 , 0.49442232, 0.5050518 , -0.20501244,
0.00771493, -0.06387987, 1.02075149, 0.51484657, 0.77049524])