Regularization¶
Agenda:¶
- Overfitting (review)
- Overfitting with linear models
- Regularization of linear models
- Regularized regression in scikit-learn
- Regularized classification in scikit-learn
- Comparing regularized linear models with unregularized linear models
Part 1: Overfitting (review)¶
What is overfitting?
- Building a model that matches the training data "too closely"
- Learning from the noise in the data, rather than just the signal
How does overfitting occur?
- Evaluating a model by testing it on the same data that was used to train it
- Creating a model that is "too complex"
What is the impact of overfitting?
- Model will do well on the training data, but won't generalize to out-of-sample data
- Model will have low bias, but high variance
Overfitting with KNN¶

Overfitting with polynomial regression¶

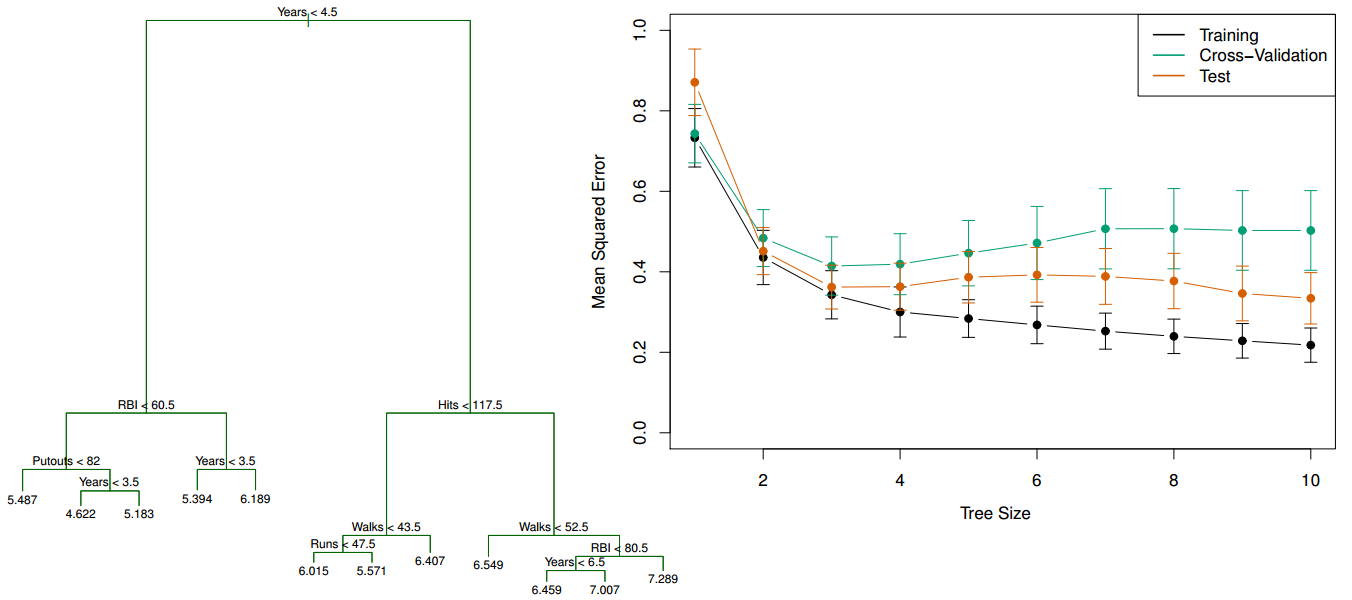
Overfitting with decision trees¶
Part 2: Overfitting with linear models¶
What are the general characteristics of linear models?
- Low model complexity
- High bias, low variance
- Does not tend to overfit
Nevertheless, overfitting can still occur with linear models if you allow them to have high variance. Here are some common causes:
Cause 1: Irrelevant features¶
Linear models can overfit if you include "irrelevant features", meaning features that are unrelated to the response. Why?
Because it will learn a coefficient for every feature you include in the model, regardless of whether that feature has the signal or the noise.
This is especially a problem when p (number of features) is close to n (number of observations), because that model will naturally have high variance.
Cause 2: Correlated features¶
Linear models can overfit if the included features are highly correlated with one another. Why?
From the scikit-learn documentation:
"...coefficient estimates for Ordinary Least Squares rely on the independence of the model terms. When terms are correlated and the columns of the design matrix X have an approximate linear dependence, the design matrix becomes close to singular and as a result, the least-squares estimate becomes highly sensitive to random errors in the observed response, producing a large variance."
Cause 3: Large coefficients¶
Linear models can overfit if the coefficients (after feature standardization) are too large. Why?
Because the larger the absolute value of the coefficient, the more power it has to change the predicted response, resulting in a higher variance.
Part 3: Regularization of linear models¶
- Regularization is a method for "constraining" or "regularizing" the size of the coefficients, thus "shrinking" them towards zero.
- It reduces model variance and thus minimizes overfitting.
- If the model is too complex, it tends to reduce variance more than it increases bias, resulting in a model that is more likely to generalize.
Our goal is to locate the optimum model complexity, and thus regularization is useful when we believe our model is too complex.

How does regularization work?¶
For a normal linear regression model, we estimate the coefficients using the least squares criterion, which minimizes the residual sum of squares (RSS):

For a regularized linear regression model, we minimize the sum of RSS and a "penalty term" that penalizes coefficient size.
Ridge regression (or "L2 regularization") minimizes: $$\text{RSS} + \alpha \sum_{j=1}^p \beta_j^2$$
Lasso regression (or "L1 regularization") minimizes: $$\text{RSS} + \alpha \sum_{j=1}^p |\beta_j|$$
- $p$ is the number of features
- $\beta_j$ is a model coefficient
- $\alpha$ is a tuning parameter:
- A tiny $\alpha$ imposes no penalty on the coefficient size, and is equivalent to a normal linear regression model.
- Increasing the $\alpha$ penalizes the coefficients and thus shrinks them.
Lasso and ridge path diagrams¶
A larger alpha (towards the left of each diagram) results in more regularization:
- Lasso regression shrinks coefficients all the way to zero, thus removing them from the model
- Ridge regression shrinks coefficients toward zero, but they rarely reach zero
Source code for the diagrams: Lasso regression and Ridge regression

Advice for applying regularization¶
Should features be standardized?
- Yes, because otherwise, features would be penalized simply because of their scale.
- Also, standardizing avoids penalizing the intercept, which wouldn't make intuitive sense.
How should you choose between Lasso regression and Ridge regression?
- Lasso regression is preferred if we believe many features are irrelevant or if we prefer a sparse model.
- If model performance is your primary concern, it is best to try both.
- ElasticNet regression is a combination of lasso regression and ridge Regression.
Visualizing regularization¶
Below is a visualization of what happens when you apply regularization. The general idea is that you are restricting the allowed values of your coefficients to a certain "region". Within that region, you want to find the coefficients that result in the best model.

In this diagram:
- We are fitting a linear regression model with two features, $x_1$ and $x_2$.
- $\hat\beta$ represents the set of two coefficients, $\beta_1$ and $\beta_2$, which minimize the RSS for the unregularized model.
- Regularization restricts the allowed positions of $\hat\beta$ to the blue constraint region:
- For lasso, this region is a diamond because it constrains the absolute value of the coefficients.
- For ridge, this region is a circle because it constrains the square of the coefficients.
- The size of the blue region is determined by $\alpha$, with a smaller $\alpha$ resulting in a larger region:
- When $\alpha$ is zero, the blue region is infinitely large, and thus the coefficient sizes are not constrained.
- When $\alpha$ increases, the blue region gets smaller and smaller.
In this case, $\hat\beta$ is not within the blue constraint region. Thus, we need to move $\hat\beta$ until it intersects the blue region, while increasing the RSS as little as possible.
From page 222 of An Introduction to Statistical Learning:
The ellipses that are centered around $\hat\beta$ represent regions of constant RSS. In other words, all of the points on a given ellipse share a common value of the RSS. As the ellipses expand away from the least squares coefficient estimates, the RSS increases. Equations (6.8) and (6.9) indicate that the lasso and ridge regression coefficient estimates are given by the first point at which an ellipse contacts the constraint region.
Since ridge regression has a circular constraint with no sharp points, this intersection will not generally occur on an axis, and so the ridge regression coefficient estimates will be exclusively non-zero. However, the lasso constraint has corners at each of the axes, and so the ellipse will often intersect the constraint region at an axis. When this occurs, one of the coefficients will equal zero. In higher dimensions, many of the coefficient estimates may equal zero simultaneously. In Figure 6.7, the intersection occurs at $\beta_1 = 0$, and so the resulting model will only include $\beta_2$.
Part 4: Regularized regression in scikit-learn¶
- Communities and Crime dataset from the UCI Machine Learning Repository: data, data dictionary
- Goal: Predict the violent crime rate for a community given socioeconomic and law enforcement data
Load and prepare the crime dataset¶
# read in the dataset
import pandas as pd
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/communities/communities.data'
crime = pd.read_csv(url, header=None, na_values=['?'])
crime.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 8 | NaN | NaN | Lakewoodcity | 1 | 0.19 | 0.33 | 0.02 | 0.90 | 0.12 | ... | 0.12 | 0.26 | 0.20 | 0.06 | 0.04 | 0.9 | 0.5 | 0.32 | 0.14 | 0.20 |
| 1 | 53 | NaN | NaN | Tukwilacity | 1 | 0.00 | 0.16 | 0.12 | 0.74 | 0.45 | ... | 0.02 | 0.12 | 0.45 | NaN | NaN | NaN | NaN | 0.00 | NaN | 0.67 |
| 2 | 24 | NaN | NaN | Aberdeentown | 1 | 0.00 | 0.42 | 0.49 | 0.56 | 0.17 | ... | 0.01 | 0.21 | 0.02 | NaN | NaN | NaN | NaN | 0.00 | NaN | 0.43 |
| 3 | 34 | 5 | 81440 | Willingborotownship | 1 | 0.04 | 0.77 | 1.00 | 0.08 | 0.12 | ... | 0.02 | 0.39 | 0.28 | NaN | NaN | NaN | NaN | 0.00 | NaN | 0.12 |
| 4 | 42 | 95 | 6096 | Bethlehemtownship | 1 | 0.01 | 0.55 | 0.02 | 0.95 | 0.09 | ... | 0.04 | 0.09 | 0.02 | NaN | NaN | NaN | NaN | 0.00 | NaN | 0.03 |
5 rows × 128 columns
# examine the response variable
crime[127].describe()
count 1994.000000 mean 0.237979 std 0.232985 min 0.000000 25% 0.070000 50% 0.150000 75% 0.330000 max 1.000000 Name: 127, dtype: float64
# remove categorical features
crime.drop([0, 1, 2, 3, 4], axis=1, inplace=True)
# remove rows with any missing values
crime.dropna(inplace=True)
# check the shape
crime.shape
(319, 123)
# define X and y
X = crime.drop(127, axis=1)
y = crime[127]
# split into training and testing sets
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
Linear regression¶
# build a linear regression model
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
linreg.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# examine the coefficients
print linreg.coef_
[ -3.66188167e+00 6.98124465e-01 -2.61955467e-01 -2.85270027e-01 -1.64740837e-01 2.46972333e-01 -1.09290051e+00 -5.96857796e-01 1.11200239e+00 -7.21968931e-01 4.27346598e+00 -2.28040268e-01 8.04875769e-01 -2.57934732e-01 -2.63458023e-01 -1.04616958e+00 6.07784197e-01 7.73552561e-01 5.96468029e-02 6.90215922e-01 2.16759430e-02 -4.87802949e-01 -5.18858404e-01 1.39478815e-01 -1.24417942e-01 3.15003821e-01 -1.52633736e-01 -9.65003927e-01 1.17142163e+00 -3.08546690e-02 -9.29085548e-01 1.24654586e-01 1.98104506e-01 7.30804821e-01 -1.77337294e-01 8.32927588e-02 3.46045601e-01 5.01837338e-01 1.57062958e+00 -4.13478807e-01 1.39350802e+00 -3.49428114e+00 7.09577818e-01 -8.32141352e-01 -1.39984927e+00 1.02482840e+00 2.13855006e-01 -6.18937325e-01 5.28954490e-01 7.98294890e-02 5.93688560e-02 -1.68582667e-01 7.31264051e-01 -1.39635208e+00 2.38507704e-01 5.50621439e-01 -5.61447867e-01 6.18989764e-01 2.55517024e+00 -3.71769599e+00 7.09191935e-01 3.82041439e-01 8.23752836e-01 -1.67703547e+00 -1.73150450e+00 9.90120171e-01 -5.72745697e-01 -1.45877295e+00 8.68032144e-01 5.15959984e-01 3.14453207e-02 2.01869791e-01 9.65291940e-02 2.13034099e+00 -6.95374423e-02 4.62477023e-02 -1.10565955e-02 -1.34313780e-02 -1.04515494e-01 -8.76985171e-01 4.26781907e-01 -1.85405795e-01 -8.16215517e-01 -2.86596076e-01 -1.56110708e-01 1.76468580e+00 -5.70163730e-01 -7.54066704e-02 -1.74212697e-01 -8.89747220e-02 2.26336403e-01 1.38030073e+00 -3.37304744e-01 -2.57856611e-02 8.91299188e-02 3.49876793e-01 -1.22428557e+00 -3.67941205e+01 -6.95699750e-01 2.95269279e-01 -1.48590316e-03 2.34206416e-01 -7.09533984e-03 3.67152957e+01 -8.90665109e-02 3.79550678e-02 3.19375782e-01 4.60708905e-01 1.41090069e-01 -6.67017320e-01 -2.59035245e-01 -4.60600755e-04 -1.51868232e-02 7.54768410e-02 -2.36105498e-03 -1.50328233e-01 1.85575558e-01 6.31979224e-01 -1.50253625e-01 1.87638817e-02 -3.38095851e-02 -4.46104032e-01]
# make predictions
y_pred = linreg.predict(X_test)
# calculate RMSE
from sklearn import metrics
import numpy as np
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.233813676495
# alpha=0 is equivalent to linear regression
from sklearn.linear_model import Ridge
ridgereg = Ridge(alpha=0, normalize=True)
ridgereg.fit(X_train, y_train)
y_pred = ridgereg.predict(X_test)
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.233813676495
# try alpha=0.1
ridgereg = Ridge(alpha=0.1, normalize=True)
ridgereg.fit(X_train, y_train)
y_pred = ridgereg.predict(X_test)
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.164279068049
# examine the coefficients
print ridgereg.coef_
[ -4.00298418e-03 3.51647445e-02 6.03535935e-02 -7.68532502e-02 -1.76099849e-02 4.53791433e-02 8.81586468e-03 -2.88885814e-02 -1.92143587e-02 3.36122201e-02 5.71590736e-04 -4.85438136e-02 5.55725157e-02 -1.15934270e-01 -1.11880845e-01 -3.32742094e-01 -1.12302031e-02 9.63833243e-02 -8.92057732e-02 8.42691702e-02 -1.67246717e-02 7.42520308e-03 -1.21294025e-01 -6.70155789e-02 -1.74250249e-03 1.69446833e-01 3.18217654e-02 -1.00209834e-01 3.97535644e-02 -1.19173054e-01 -1.04445267e-01 -5.14946676e-03 1.10071013e-01 -3.22958955e-02 -1.40601627e-01 7.72658029e-02 9.07962536e-02 -3.78878862e-03 4.61941793e-02 6.30299731e-02 -3.09236932e-02 1.02883578e-02 9.70425568e-02 -1.28936944e-01 -1.38268907e-01 -6.37169778e-02 -8.80160419e-02 -4.01991014e-02 8.11064596e-02 -6.30663975e-02 1.29756859e-01 -6.25210624e-02 1.60531213e-02 -1.39061824e-01 6.39822353e-02 4.87118744e-02 -7.68217532e-03 -1.53523412e-03 1.73028280e-02 -1.37258659e-03 -1.97381922e-02 4.47492477e-02 3.53941624e-03 -1.64126843e-02 -1.62363185e-02 7.10860268e-02 -1.34543849e-01 3.03401863e-02 2.87012058e-02 2.62507811e-01 3.87946361e-02 4.16976393e-02 2.45959130e-02 4.02803695e-02 -1.15568319e-02 1.82352709e-02 -1.11769965e-04 1.17220288e-02 -3.27960499e-02 -2.06336390e-02 -2.01424775e-02 -1.55746075e-02 -1.50471159e-01 5.00237268e-02 1.67270388e-02 1.27989507e-01 -7.55437715e-02 -7.22756020e-02 -8.80283128e-02 6.42301728e-02 1.39781081e-01 4.71861289e-02 -6.42667056e-02 3.16227166e-02 -1.36066226e-02 5.16507328e-02 -4.60206271e-02 6.55072592e-04 3.51488294e-02 -1.68717518e-02 -7.00033520e-03 4.99335627e-02 8.40464679e-02 3.87553978e-03 -1.23632746e-01 -2.24505480e-02 -2.47960018e-03 4.13468551e-02 8.26295505e-02 -4.84167513e-02 8.21329530e-03 1.57843967e-02 -1.94698620e-02 4.09120489e-02 -4.42911592e-02 -5.64373896e-02 1.17841094e-01 7.34994342e-02 -2.78153968e-02 3.74136314e-02 -7.67878399e-02 -4.65440973e-02]
- RidgeCV: ridge regression with built-in cross-validation of the alpha parameter
- alphas: array of alpha values to try
# create an array of alpha values
alpha_range = 10.**np.arange(-2, 3)
alpha_range
array([ 1.00000000e-02, 1.00000000e-01, 1.00000000e+00,
1.00000000e+01, 1.00000000e+02])
# select the best alpha with RidgeCV
from sklearn.linear_model import RidgeCV
ridgeregcv = RidgeCV(alphas=alpha_range, normalize=True, scoring='mean_squared_error')
ridgeregcv.fit(X_train, y_train)
ridgeregcv.alpha_
1.0
# predict method uses the best alpha value
y_pred = ridgeregcv.predict(X_test)
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.163129782343
# try alpha=0.001 and examine coefficients
from sklearn.linear_model import Lasso
lassoreg = Lasso(alpha=0.001, normalize=True)
lassoreg.fit(X_train, y_train)
print lassoreg.coef_
[ 0. 0. 0.00891952 -0.27423369 0. 0. 0. -0. -0. 0. 0. 0. -0. -0. -0. -0.19414627 0. 0. -0. -0. -0. -0. -0. -0. -0. 0. 0. 0. 0.04335664 -0. 0. -0. 0.03491474 -0. -0.06685424 0. 0. -0. 0.10575313 0. 0. 0.00890807 0. -0.1378172 -0.30954312 -0. -0. -0. -0. 0. 0. 0. 0. -0. 0. 0. 0. 0. 0. 0. -0. 0. 0. 0. -0. 0. -0. -0. 0. 0.05257892 -0. 0. -0. -0. 0. 0. 0. 0. 0. -0. -0. -0. -0. -0. -0. -0. 0. -0. -0. 0. 0.13861081 0. -0. -0. 0. 0. 0. 0. -0. 0. 0. 0. 0.03347908 0. -0.01130055 -0. 0. 0. 0.00044205 0. 0. 0. -0. 0. -0. -0. 0.04153636 0. -0. 0.00719672 -0.000666 0. ]
# try alpha=0.01 and examine coefficients
lassoreg = Lasso(alpha=0.01, normalize=True)
lassoreg.fit(X_train, y_train)
print lassoreg.coef_
[ 0. 0. 0. -0.03974695 0. 0. 0. 0. 0. -0. 0. 0. -0. -0. -0. -0. -0. 0. -0. -0. -0. -0. -0. -0. -0. -0. -0. 0. 0. 0. 0. -0. 0. -0. -0. 0. 0. -0. 0. 0. 0. 0. 0. -0. -0.27503063 -0. -0. -0. -0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -0. 0. 0. 0. 0. 0. 0. -0. 0. 0. -0. 0. -0. -0. 0. 0. -0. 0. 0. -0. -0. -0. -0. -0. -0. -0. 0. 0. -0. 0. 0. 0. 0. -0. 0. 0. 0. 0. -0. 0. 0. 0. 0. 0. -0. -0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. -0. 0. -0. 0. ]
# calculate RMSE (for alpha=0.01)
y_pred = lassoreg.predict(X_test)
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.198165225429
- LassoCV: lasso regression with built-in cross-validation of the alpha parameter
- n_alphas: number of alpha values (automatically chosen) to try
# select the best alpha with LassoCV
from sklearn.linear_model import LassoCV
lassoregcv = LassoCV(n_alphas=100, normalize=True, random_state=1)
lassoregcv.fit(X_train, y_train)
lassoregcv.alpha_
c:\Users\Kevin\Anaconda\lib\site-packages\sklearn\linear_model\coordinate_descent.py:444: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations ConvergenceWarning)
0.0015161594598125873
# examine the coefficients
print lassoregcv.coef_
[ 0. 0. 0. -0.28113506 0. 0. 0. 0. 0. 0. 0. 0. -0. -0. -0. -0.15481092 0. 0. -0. -0. -0. -0. -0. -0. -0. 0. -0. 0. 0.06451487 0. 0. -0. 0. -0. -0.01920421 0. 0. -0. 0.03386202 0. 0. 0.08901243 0. -0.08759757 -0.36986917 -0. -0. -0. -0. 0. 0. 0. 0. -0. 0. 0. 0. 0. 0. 0. -0. 0. 0. 0. -0. 0. 0. -0. 0. 0.01740599 -0. 0. -0. -0. 0. 0. 0. 0. 0. -0. -0. -0. -0. -0. -0. -0. 0. -0. -0. 0. 0.13471036 0. -0. -0. 0. -0. 0. 0. -0. 0. 0. 0. 0.0054122 0. -0. -0. 0. 0. 0. 0. 0. 0. -0. 0. -0. 0. 0.02738796 0. -0. 0. -0. 0. ]
# predict method uses the best alpha value
y_pred = lassoregcv.predict(X_test)
print np.sqrt(metrics.mean_squared_error(y_test, y_pred))
0.160209558014
Part 5: Regularized classification in scikit-learn¶
- Wine dataset from the UCI Machine Learning Repository: data, data dictionary
- Goal: Predict the origin of wine using chemical analysis
Load and prepare the wine dataset¶
# read in the dataset
url = 'http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data'
wine = pd.read_csv(url, header=None)
wine.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.80 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065 |
| 1 | 1 | 13.20 | 1.78 | 2.14 | 11.2 | 100 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050 |
| 2 | 1 | 13.16 | 2.36 | 2.67 | 18.6 | 101 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185 |
| 3 | 1 | 14.37 | 1.95 | 2.50 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 | 7.80 | 0.86 | 3.45 | 1480 |
| 4 | 1 | 13.24 | 2.59 | 2.87 | 21.0 | 118 | 2.80 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735 |
# examine the response variable
wine[0].value_counts()
2 71 1 59 3 48 dtype: int64
# define X and y
X = wine.drop(0, axis=1)
y = wine[0]
# split into training and testing sets
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
Logistic regression (unregularized)¶
# build a logistic regression model
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression(C=1e9)
logreg.fit(X_train, y_train)
LogisticRegression(C=1000000000.0, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1, max_iter=100,
multi_class='ovr', penalty='l2', random_state=None,
solver='liblinear', tol=0.0001, verbose=0)
# examine the coefficients
print logreg.coef_
[[ -4.15397186e+00 4.90075538e+00 1.53790183e+01 -2.85235942e+00
1.10505593e-01 -5.30164453e+00 1.05110893e+01 3.06125855e+00
-1.18150745e+01 -2.43836649e+00 -1.80124471e+00 7.09007536e+00
6.93945792e-02]
[ 5.43369566e+00 -5.23569200e+00 -1.67764364e+01 1.64044307e+00
5.76913231e-03 2.82443590e+00 4.90939605e+00 2.45082648e+00
6.08259423e+00 -7.85245282e+00 3.48485003e+00 -7.70842670e+00
-4.90936762e-02]
[ -9.70207612e-01 2.08269720e+00 9.41526165e-01 2.38023989e-01
-2.49596817e-03 -9.80981243e-01 -6.54889317e+00 -4.83302817e-01
-2.65888456e+00 2.57458669e+00 -1.30417032e+00 -2.34300175e+00
9.48521802e-03]]
# generate predicted probabilities
y_pred_prob = logreg.predict_proba(X_test)
print y_pred_prob
[[ 4.08866128e-10 3.95149488e-10 9.99999999e-01] [ 4.06722935e-17 1.00000000e+00 4.32260610e-10] [ 9.99999906e-01 3.46933978e-11 9.37658044e-08] [ 4.64048343e-09 9.99999871e-01 1.24115833e-07] [ 9.99730854e-01 3.16142539e-21 2.69146225e-04] [ 1.42243183e-14 8.09034805e-07 9.99999191e-01] [ 9.99829153e-01 1.47180023e-05 1.56129392e-04] [ 9.99999720e-01 1.24359831e-23 2.80079015e-07] [ 1.62930410e-17 3.49895213e-13 1.00000000e+00] [ 1.97059220e-16 9.99997008e-01 2.99222229e-06] [ 9.99967664e-01 2.23795926e-12 3.23360924e-05] [ 9.73457858e-01 2.65419232e-02 2.19064985e-07] [ 2.84224171e-20 1.00000000e+00 1.12562075e-10] [ 9.99999998e-01 1.32844859e-13 1.72600662e-09] [ 3.69546813e-09 9.99999996e-01 3.47691845e-10] [ 4.22805011e-15 9.99999959e-01 4.13233076e-08] [ 3.35466649e-29 4.79623565e-01 5.20376435e-01] [ 9.99960400e-01 3.95740340e-05 2.64337565e-08] [ 3.29043791e-14 9.99999930e-01 7.00568466e-08] [ 9.99778348e-01 4.17075187e-21 2.21651755e-04] [ 9.99999731e-01 2.62889100e-15 2.69237974e-07] [ 6.19900193e-16 1.00000000e+00 2.86953165e-11] [ 2.77940112e-09 9.69506740e-01 3.04932569e-02] [ 5.28754692e-05 9.99947121e-01 3.47404069e-09] [ 9.99947715e-01 5.22837028e-05 1.10248529e-09] [ 5.82332195e-13 2.38782109e-08 9.99999976e-01] [ 9.99999788e-01 2.08506990e-07 3.11782661e-09] [ 9.99999791e-01 6.12671899e-08 1.47460916e-07] [ 9.99986850e-01 8.10206146e-14 1.31497566e-05] [ 9.54043555e-12 3.72425979e-19 1.00000000e+00] [ 3.04071238e-11 1.00000000e+00 4.08122442e-11] [ 3.50017326e-31 3.81668757e-19 1.00000000e+00] [ 1.42219468e-22 6.83344681e-19 1.00000000e+00] [ 9.99995753e-01 3.04811377e-20 4.24748096e-06] [ 2.79451178e-01 7.20548821e-01 1.13159945e-09] [ 5.67756081e-11 9.99999996e-01 3.89757045e-09] [ 2.41389951e-17 9.99932283e-01 6.77171026e-05] [ 2.28608435e-03 9.97713901e-01 1.48456046e-08] [ 2.93122189e-12 9.99999997e-01 3.22321411e-09] [ 9.99998259e-01 3.53259025e-08 1.70528897e-06] [ 9.99999019e-01 1.03943395e-11 9.80508127e-07] [ 3.41369632e-09 9.99903436e-01 9.65610816e-05] [ 2.55526052e-20 7.80550210e-08 9.99999922e-01] [ 9.99999985e-01 3.33192992e-10 1.45026119e-08] [ 9.99999917e-01 3.19711403e-09 7.96376715e-08]]
# calculate log loss
print metrics.log_loss(y_test, y_pred_prob)
0.347281798715
Logistic regression (regularized)¶
- LogisticRegression documentation
- C: must be positive, decrease for more regularization
- penalty: l1 (lasso) or l2 (ridge)
# standardize X_train and X_test
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# try C=0.1 with L1 penalty
logreg = LogisticRegression(C=0.1, penalty='l1')
logreg.fit(X_train_scaled, y_train)
print logreg.coef_
[[ 0.21044571 0. 0. 0. 0. 0. 0.48723077 0. 0. 0. 0. 0.15360853 1.47743702] [-0.65689319 -0.05651272 -0.11386446 0. 0. 0. 0. 0. 0. -0.73862636 0.24344904 0. -0.63405624] [ 0. 0. 0. 0. 0. 0. -0.84238099 0. 0. 0.61559726 -0.49014626 -0.30427496 0. ]]
# generate predicted probabilities and calculate log loss
y_pred_prob = logreg.predict_proba(X_test_scaled)
print metrics.log_loss(y_test, y_pred_prob)
0.362248219747
# try C=0.1 with L2 penalty
logreg = LogisticRegression(C=0.1, penalty='l2')
logreg.fit(X_train_scaled, y_train)
print logreg.coef_
[[ 0.59163934 0.06886667 0.33592964 -0.49616684 0.111539 0.21570086 0.40524509 -0.15526139 -0.02534651 0.05399014 0.14877346 0.42327938 0.89815007] [-0.73545676 -0.32942948 -0.47995296 0.294866 -0.1500246 0.04264373 0.14500586 0.07250763 0.17409795 -0.70726652 0.4128986 0.09997212 -0.81284365] [ 0.20136567 0.30989025 0.15977925 0.18867218 0.04204443 -0.27108109 -0.55886639 0.07486943 -0.17471153 0.68266464 -0.52385748 -0.49566967 -0.02565631]]
# generate predicted probabilities and calculate log loss
y_pred_prob = logreg.predict_proba(X_test_scaled)
print metrics.log_loss(y_test, y_pred_prob)
0.244588324539
- Pipeline: chain steps together
- GridSearchCV: search a grid of parameters
# pipeline of StandardScaler and LogisticRegression
from sklearn.pipeline import make_pipeline
pipe = make_pipeline(StandardScaler(), LogisticRegression())
# grid search for best combination of C and penalty
from sklearn.grid_search import GridSearchCV
C_range = 10.**np.arange(-2, 3)
penalty_options = ['l1', 'l2']
param_grid = dict(logisticregression__C=C_range, logisticregression__penalty=penalty_options)
grid = GridSearchCV(pipe, param_grid, cv=10, scoring='log_loss')
grid.fit(X, y)
GridSearchCV(cv=10, error_score='raise',
estimator=Pipeline(steps=[('standardscaler', StandardScaler(copy=True, with_mean=True, with_std=True)), ('logisticregression', LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, max_iter=100, multi_class='ovr',
penalty='l2', random_state=None, solver='liblinear', tol=0.0001,
verbose=0))]),
fit_params={}, iid=True, loss_func=None, n_jobs=1,
param_grid={'logisticregression__penalty': ['l1', 'l2'], 'logisticregression__C': array([ 1.00000e-02, 1.00000e-01, 1.00000e+00, 1.00000e+01,
1.00000e+02])},
pre_dispatch='2*n_jobs', refit=True, score_func=None,
scoring='log_loss', verbose=0)
# print all log loss scores
grid.grid_scores_
[mean: -1.09861, std: 0.00000, params: {'logisticregression__penalty': 'l1', 'logisticregression__C': 0.01},
mean: -0.62547, std: 0.03037, params: {'logisticregression__penalty': 'l2', 'logisticregression__C': 0.01},
mean: -0.35491, std: 0.06891, params: {'logisticregression__penalty': 'l1', 'logisticregression__C': 0.10000000000000001},
mean: -0.26801, std: 0.04840, params: {'logisticregression__penalty': 'l2', 'logisticregression__C': 0.10000000000000001},
mean: -0.09436, std: 0.06114, params: {'logisticregression__penalty': 'l1', 'logisticregression__C': 1.0},
mean: -0.10371, std: 0.04894, params: {'logisticregression__penalty': 'l2', 'logisticregression__C': 1.0},
mean: -0.05837, std: 0.06413, params: {'logisticregression__penalty': 'l1', 'logisticregression__C': 10.0},
mean: -0.06174, std: 0.05651, params: {'logisticregression__penalty': 'l2', 'logisticregression__C': 10.0},
mean: -0.07142, std: 0.09266, params: {'logisticregression__penalty': 'l1', 'logisticregression__C': 100.0},
mean: -0.06443, std: 0.08409, params: {'logisticregression__penalty': 'l2', 'logisticregression__C': 100.0}]
# examine the best model
print grid.best_score_
print grid.best_params_
-0.0583689728556
{'logisticregression__penalty': 'l1', 'logisticregression__C': 10.0}
Part 6: Comparing regularized linear models with unregularized linear models¶
Advantages of regularized linear models:
- Better performance
- L1 regularization performs automatic feature selection
- Useful for high-dimensional problems (p > n)
Disadvantages of regularized linear models:
- Tuning is required
- Feature scaling is recommended
- Less interpretable (due to feature scaling)