Chapter 7 - Searching large Collections of Text¶
-- A Python Course for the Humanities
Imagine you have collected a large number of documents for your research. A large collection of English novels from Project Gutenberg, for example, or all volumes of the New York Times from 1987 until 2007 (see here). The New York Times corpus contains over 1.8 million articles. If on average each article consists of only 500 words (the actual number will probably be higher), the complete corpus will contain about 900 million words. How can we search through such large collections of text? How can we efficiently find the information we are looking for?
These questions are central to the current chapter. We will discuss important concepts from Information Retrieval to index and search collections (of text), such as the inverted index and the ranking metric Okapi BM25. This wouldn't be a Python course if you didn't have to implement all discussed techniques and methods. We will implement an important search algorithm which allows you to efficiently and reliably extract information from corpora. Along the way we will discuss quite some new and important programming techniques and constructs. We will also further our knowledge about the framework of Object Oriented Programming or OOP. We have quite some ground to cover, so let's get started.
Indexing Collections of Text¶
Information Retrieval (IR) is finding material (usually documents) of an unstructured nature (usually text) that satisfies an information need from within large collections (usually stored on computers. (Manning, NLP course, coursera)
The field of Information Retrieval (IR) deals with developing techniques that allow users to efficiently search through large collections (of text) to find documents that are relevant to the question a particular user has. These days we almost immediately think of web search in the context of IR, but there are many other use case scenarios, such as E-mail search, searching for music (e.g. Spotify) or searching for content on your laptop.
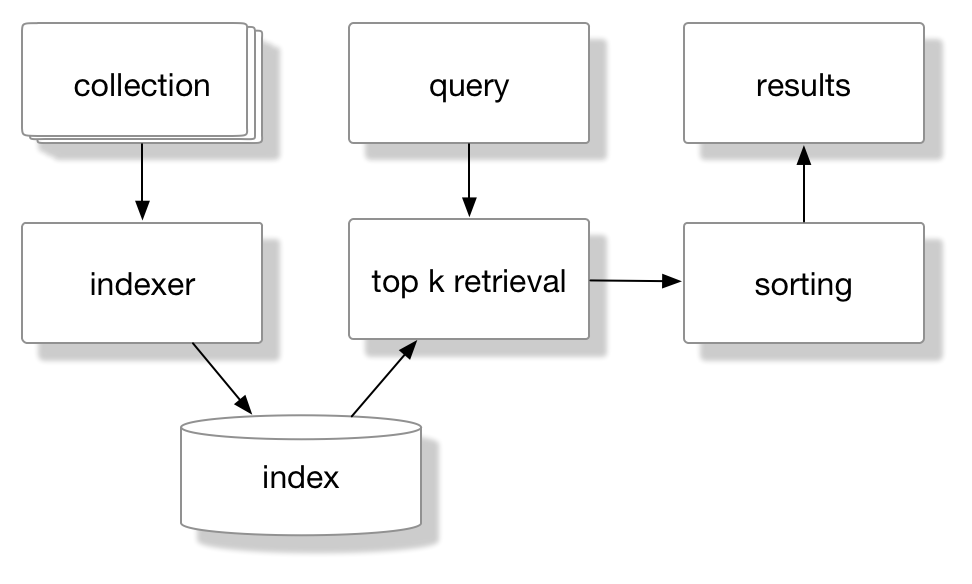
Most search models in Information Retrieval are similar to the schema above. We have a collection of items, text documents, for example, that are indexed using an indexer with a particular indexing schema. Given a user query, the index is used to retrieve $k$ documents which, after scoring and sorting, are presented to the user. This might seem all a little abstract, but it will all become clear once we start implementing our own IR system.
Consider a newspaper collection covering the complete 20th century. In this collection we would like to find all documents that mention Albert Einstein and Edwin Hubble but not Enrico Fermi. Those of you familiar with the unix search tool grep might argue that we could simply use grep to search for all documents that contain both Einstein and Hubble and then filter out those documents that mention Fermi.
Quiz!¶
Come up with at least two reasons why searching with grep is not a good option.
Double click this cell and write down your answer.
Term Document Incidence Matrix¶
To efficiently give an answer to such queries we need to come up with another representation of our collection instead of plain text. Have a look at the following table.
| 12-11-1928 | 04-04-1946 | 03-11-1983 | 19-01-1999 | |
|---|---|---|---|---|
| Einstein | 1 | 1 | 0 | 0 |
| Hubble | 1 | 1 | 1 | 0 |
| Fermi | 1 | 0 | 0 | 0 |
| Winfrey | 0 | 0 | 0 | 1 |
| Dylan | 0 | 0 | 1 | 1 |
This table is called a Term Document incidence matrix where for each term (rows) we write down a 1 if a particular document (columns) contains that term and 0 otherwise. In this representation each term is represented by an incidence vector. If we want to extract all documents that mention Albert Einstein, we can use the binary vector 1100 of Einstein to quickly extract all documents mentioning Einstein. To find all documents containing both Einstein and Hubble we take the complement of the vectors of Einstein (1100) and Hubble (1110):
1100 AND 1110 = 1100
Quiz!¶
a) Given the incidence vectors of Einstein (1100), Hubble (1110) and Fermi (1000), what is the binary representation corresponding to the query Einstein AND Hubble AND NOT Fermi?
Double click this cell and write down your answer.
b) Can you implement the function AND that takes as argument two incidence vectors (represented a binary lists in Python) and returns the complement of the two?
def AND(vector_a, vector_b):
# insert your code here
# these tests should return True if your code is correct
print(AND([1, 1, 0, 0], [1, 1, 1, 0]) == [1, 1, 0, 0])
print(AND([1, 0, 0, 1, 0, 0, 1], [1, 1, 1, 0, 1, 0, 1]) == [1, 0, 0, 0, 0, 0, 1])
c) Rewrite the function AND to allow it to take an arbitary number of incidence vectors.
def AND(*vectors):
# insert your code here
# these tests should return True if your code is correct
print(AND([1, 1, 0, 0], [1, 1, 1, 0], [1, 0, 0, 0]) == [1, 0, 0, 0])
print(AND([1, 1, 1, 0, 1], [1, 0, 0, 1, 0], [0, 1, 1, 0, 1]) == [0, 0, 0, 0, 0])
d) Implement the function NOT. It takes as argument an incidence vector and returns a representation that can be used in combination with AND queries.
def NOT(vector):
# insert your code here
# these tests should return True if your code is correct
print(AND([1, 1, 0, 0], [1, 1, 1, 0], NOT([1, 0, 0, 0])) == [0, 1, 0, 0])
The binary representation allows us to efficiently search for documents containing particular terms of a search query. There are, however, still some problems that need to be overcome. Consider a document collection of 1 million documents where each document is about a thousand words long. On average such a collection contains approximately 500k unique terms. This means that if we try to build an incidence matrix, we would have to construct a matrix containing $500,000 \times 1,000,000 =$ half a trillion 0's and 1's. Such a large matrix cannot be stored on a simple laptop.
Quiz!¶
a) Much of the information in the matrix is redundant. Why?
Double click this cell and write down your answer.
b) What would be a better representation of our matrix?
Double click this cell and write down your answer.
Inverted Index¶
The Inverted Index is the key data structure in modern Information Retrieval. An inverted index is a structure in which for each unique term $t$ in our collection, we store a list of all document ID's that contain $t$. If we represent our small collection of newspapers in this way, it looks like this:
Einstein: [12-11-1928, 04-04-1946]
Hubble: [12-11-1928, 04-04-1946, 03-11-1983]
Fermi: [12-11-1928]
Winfrey: [19-01-1999]
Dylan: [03-11-1983, 19-01-1999]
Quiz!¶
a) What would be a convenient and efficient data structure in Python to represent an inverted index?
Double click this cell and write down your answer.
b) We will implement a first version of an IR system. I choose to implement it as the class IRSystem. Implement the method index_document. It takes as argument a document ID and a list of words. The function should update the variable tdf in such a way that for each term it stores a set of all document IDs in which that term occurs.
import glob, os, re
from collections import defaultdict
def tokenize(text, lowercase=True):
text = text.lower() if lowercase else text
for match in re.finditer(r"\w+(\.?\w+)*", text):
yield match.group()
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several documents
with s.index_document(ID, text).
"""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(set)
self.doc_ids = []
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
# insert your code here
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
# these tests should return True if your code is correct
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
print('The Ghost Kings 8184.txt' in s.tdf['master'])
print('Cleopatra 2769.txt' in s.tdf['children'])
Query the Index¶
Now that we have an efficient, sparse data structure to represent our collection, how can we use that stucture to efficiently process user queries? Our index is represented as a Python dictionary which allows us to query the index for single terms, using
s = IRSystem()
s.tdf[term]
which will return a set of all documents in which that term occurs. But how do we search for documents that contain two or more terms? Python's data structure set defines a convenient method called intersection with which we can extract all items common to two or more sets:
a = {'a', 'b', 'c', 'd'}
b = {'c', 'a', 'e', 'f'}
print(a.intersection(b))
We can make use of this method to implement the method query which takes as argument an arbitrary number of query terms and returns all documents in which those terms occur.
Quiz!¶
Implement the method IRSystem.query(*terms). The method should return an iterable containing all ID's of the documents in which all query terms occur.
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several documents
with s.index_document(ID, text). Then ask queries with
s.query('term1', 'term2') to retrieve the matching documents."""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(set)
self.doc_ids = []
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
for word in words:
self.tdf[word].add(doc_id)
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def query(self, *terms):
"Query the system for documents in which all terms occur."
# insert your code here
# these tests should return True if your code is correct
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
print('Beatrice 3096.txt' in s.query("master", "children"))
print('Fair Margaret 9780.txt' in s.query("eye", "father", "work"))
Our Information Retrieval system starts to look quite good. We have written functions to tokenize documents, index documents and query the index for documents. In the query method above, we made the simplifying assumption that as long as two documents contain a particular search term, they are equally relevant. However, our intuition says that documents that contain more instances of a particular term are more relevant than documents with less instances. To account for this intuition we need a way to score and sort our search results.
Let's start with a very naive and simple scoring function: document frequency. This scoring function simply sums the document frequencies of each search term in a particular document:
$$\textrm{score}(q_1, q_2, \ldots, q_n) = \sum^n_{i=1} df(q_i)$$where $n$ is the number of search terms and $df$ the document frequency of term $q_i$ in a document.
To compute this formula we need to obtain the frequency of each word in each document. The method index_document seems an appropriate place to extract these frequencies. For each term we store how often that term occurs in each document. Note that in the previous implementation of index_document, the variable tdf is represented by a dictionary with sets of document ID's as values. We will change this data structure to a structure that allows us to store the document frequencies:
from collections import Counter
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several documents
with s.index_document(ID, text). Then ask queries with
s.query('term1', 'term2') to retrieve the matching documents."""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(Counter) # changed!
self.doc_ids = []
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
for word in words:
self.tdf[word][doc_id] += 1 # changed!
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def query(self, *terms):
"Query the system for documents in which all terms occur."
return set.intersection(*map(self.tdf.get, terms))
I represent the tdf variable as a dictionary with Counter objects as default values. The Counter object is a very convenient structure for counting hashable objects. As you can see, we only had to adjust two lines in our original system. Before we continue, make sure you understand what is happening here. We reinitialize our IR system:
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
Let's inspect the term-document frequency matrix:
s.tdf['master'].most_common(n=10)
The class Counter has a method called most_common. It returns the $n$ most common items in a Counter object. We have a data structure that stores the information about the frequency of words in documents. The next step will be to to adapt our query function in such a way that it returns a ranked list of documents where each document is sorted on the basis of the equation above.
Quiz!¶
a) The method query in the class definition below calls the method score. This method takes as arguments a document ID and an arbitrary number of terms. It returns the sum of the frequencies of these terms in this document. Implement the method score.
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several
documents with s.index_document(ID, text). Then ask queries
with s.query('term1', 'term2') to retrieve the top n matching
documents."""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(Counter)
self.doc_ids = []
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
for word in words:
self.tdf[word][doc_id] += 1
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def score(self, doc_id, *terms):
"Score a document for a particular query using the sum of the term frequencies."
# insert your code here
def query(self, *terms, n=10):
"""Query the system for documents in which all terms occur. Returns
the top n matching documents."""
scores = {doc_id: self.score(doc_id, *terms) for doc_id in self.doc_ids}
return sorted(scores, key=scores.get, reverse=True)[:n]
# these tests should return True if your code is correct
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
print(s.query("master")[0] == 'The Ancient Allan 5746.txt')
print(s.query("egg", "shell")[0] == 'Dawn 10892.txt')
b) Give at least two reasons why this way of scoring and sorting our documents is probably not such a good idea, after all.
Double click this cell and write down your answer.
Okapi BM25¶
Our scoring method contains multiple flaws. Most worrying is that it does not control for the lengths of our documents. Needless to say, this greatly influences our final lists. We need to think harder about what makes it that a search term is more or less relevant for a particular document.
The frequency with which terms occur in a document functions as an important cue to the importance of a document. The document is even more important when it contains many examples of this search term while the term occurs only in a limited number of other documents. In Information Retrieval a ranking metric that attempts to capture this intuition is Okapi BM25. The metric has proven to be one of the most successful ranking functions. In one of its many versions it is computed as follows:
$$score(q_1, q_2, \ldots, q_n) = \sum^n_{i=1} IDF(q_i) \cdot \frac{df(q_i, D) \cdot (k_1 + 1)}{df(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{\textrm{avgdl}})}$$where $Q$ represents a query and $df(q_i, D)$ is the frequency of the i'th term in $Q$ in document $D$. $|D|$ is the length of document $D$ in number of word tokens and avgdl is the average document length. The parameters $b$ and $k_1$ are commonly set to $0.75$ and $1.2$, respectively. We compute the I(nverse) D(ocument) F(requency) weight using:
$$IDF(q_i) = \log \frac{N - n(q_i) + 0.5}{n(q_i) + 0.5}$$where $N$ is the number of documents in the corpus and $n(q_i)$ the number of documents that contain $q_i$.
We will implement this formula in our score method. Before we do that, we will first make a list of all the information we need to compute the formula:
- the frequency of a term $q_i$ in document $D$;
- the length of document $D$;
- the average length of all documents in the collection;
- the IDF weight of a term $q_i$.
Our current implementation already stores the document frequency of each term in each document (1). Thus, we only need to write code to extract the last three items: (2) the length of each document, (3) the average document length and (4) the IDF weight of each unique term.
Quiz!¶
a) In this exercise you have to add the length of each document in our collection to the IR system. Reimplement the index_document method. Besides updating the term-document frequencies of each term, it should update the Counter object lengths in such a way that for each document ID it stores the length of the document being indexed.
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several
documents with s.index_document(ID, text). Then ask queries
with s.query('term1', 'term2') to retrieve the top n matching
documents."""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(Counter)
self.lengths = Counter()
self.doc_ids = []
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
# insert your code here
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def score(self, doc_id, *terms):
"Score a document for a particular query using the sum of the term frequencies."
return sum(self.tdf[term][doc_id] for term in terms)
def query(self, *terms, n=10):
"""Query the system for documents in which all terms occur. Returns
the top n matching documents."""
scores = {doc_id: self.score(doc_id, *terms) for doc_id in self.doc_ids}
return sorted(scores, key=scores.get, reverse=True)[:n]
# these tests should return True if your code is correct
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
print(s.lengths['Dawn 10892.txt'] == 192299)
b) Once we have obtained the document length for each document, computing the average document length is trivial. In this exercise we will focus on the IDF weights. To compute the IDF weight for a particular term $q_i$ we need to know two things:
- how many documents $N$ there are in our collection;
- in how many documents that term occurs: $n(q_i)$.
We will implement a helper method called _document_frequency. It should return a dictionary in which we store for each term the number of documents in which that term occurs. You will also need to adapt the index_document method in such a way that the variable N represents the number of documents that have been indexed.
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several
documents with s.index_document(ID, text). Then ask queries
with s.query('term1', 'term2') to retrieve the top n matching
documents."""
def __init__(self):
"Initialize an IR Sytem."
self.tdf = defaultdict(Counter)
self.lengths = Counter()
self.doc_ids = []
self.N = 0
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.doc_ids.append(doc_id)
# insert you code here
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def _document_frequency(self):
"Return the document frequency for each term in self.tdf."
# insert your code here
def score(self, doc_id, *terms):
"Score a document for a particular query using the sum of the term frequencies."
return sum(self.tdf[term][doc_id] for term in terms)
def query(self, *terms, n=10):
"""Query the system for documents in which all terms occur. Returns
the top n matching documents."""
scores = {doc_id: self.score(doc_id, *terms) for doc_id in self.doc_ids}
return sorted(scores, key=scores.get, reverse=True)[:n]
# these tests should return True if your code is correct
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
print(s._document_frequency()['children'] == 59)
We now have all the ingredients to compute the Okapi BM25 score. Lets put everything together and implement a complete version of our IR system:
import glob, os
from math import log
class IRSystem:
"""A very simple Information Retrieval System. The constructor
s = IRSystem() builds an empty system. Next, index several documents
with s.index_document(text, url). Then ask queries with
s.query('term1', 'term2', n=10) to retrieve the top n
matching documents."""
def __init__(self, b=0.75, k1=1.2):
"Initialize an IR Sytem."
self.N = 0
self.lengths = Counter()
self.tdf = defaultdict(Counter)
self.doc_ids = []
self.b = b
self.k1 = k1
self._all_set = False
def __repr__(self):
return '<IRSystem(b={self.b}, k1={self.k1}, N={self.N})>'.format(self=self)
def index_document(self, doc_id, words):
"Add a new unindexed document to the system."
self.N += 1
self.doc_ids.append(doc_id)
for word in words:
self.tdf[word][doc_id] += 1
self.lengths[doc_id] += 1
self._all_set = False
def index_collection(self, filenames):
"Index a collection of documents."
for filename in filenames:
self.index_document(os.path.basename(filename),
tokenize(open(filename).read()))
def _document_frequency(self):
"Return the document frequency for each term in self.tdf."
return {term: len(documents) for term, documents in self.tdf.items()}
def score(self, doc_id, *query):
"Score a document for a particular query using Okapi BM25."
score = 0
length = self.lengths[doc_id]
for term in query:
tf = self.tdf[term][doc_id]
df = self.df.get(term, 0)
idf = log((self.N - df + 0.5) / (df + 0.5))
score += (idf * (tf * (self.k1 + 1)) /
(tf + self.k1 * (1 - self.b + (self.b * length / self.avg_len))))
return score
def query(self, *query, n=10):
"""Query an indexed collection. Returns a ranked list of doc ID's sorted by
the computation of Okapi BM25."""
if not self._all_set:
self.df = self._document_frequency()
self.avg_len = sum(self.lengths.values()) / self.N
self._all_set = True
scores = {doc_id: self.score(doc_id, *query) for doc_id in self.doc_ids}
return sorted(scores.items(), key=lambda i: i[1], reverse=True)[:n]
def present(self, results):
"Present the query results as a list."
for doc_id, score in results:
print("%5.2f | %s" % (100 * score, doc_id))
def present_results(self, *query):
"Query the collection and present the results."
return self.present(self.query(*query))
I have taken the liberty to make some minor adjustments to the class and add some methods to present the results of a query. The method score implements Okapi BM25 quite straightforwardly. Note that I added a boolean attribute called _all_set to the class. This attribute tells the system whether all the pieces of information to compute the Okapi BM25 scores have been collected. In the method query we ask whether all is set. If not, we first compute the document frequencies of each unique term in our collection as well as the average document length. The reason I do not compute this earlier is that after a document has been added to the index, we need to recompute all these values (note that we set _all_set in index_document to False). Since we do not know whether a user of this class will add some more documents after having indexed a complete collection earlier, it is safer to postpone these computations. The methods present and present_results are two helper methods to more conveniently print the results of a query.
Let's test out IR System!
s = IRSystem()
s.index_collection(glob.glob('data/haggard/*.txt'))
s.present_results("regeneration", "pharao", "odds")
Final exercise¶
Perhaps the biggest advantage of Object Oriented Programming is the ability to subclass objects. You could, for example, make a specialized IRSystem for searching through particular directories on your own laptop. In this final exercise you will implement a simple web searcher. This searcher can be initialized with a number of URLs of web pages. The searcher downloads these pages, strips all HTML markup and indexes the raw text. The searcher can then be used to query for particular web pages.
Our implementation starts with a function to retrieve a webpage given a URL. The module urllib.request in Python's standard library, defines a number of functions and classes to open and read URLs. The function urlopen opens a HTTPResponse object, which has a method called read. Upon calling the read method, the complete webpage will be downloaded:
import urllib.request
response = urllib.request.urlopen("https://en.wikipedia.org/wiki/Albert_einstein")
response.read()[:1000]
The transcendent BeautifulSoup is a package to parse and create HTML (and a lot more). We will use this package to read the web pages:
from bs4 import BeautifulSoup
response = urllib.request.urlopen("https://en.wikipedia.org/wiki/Albert_einstein")
page = BeautifulSoup(response.read())
We call the method get_text on this web page to obtain a textual representation of the web page.
text = page.get_text()
print(text[-1000:])
a) Implement the function fetch_page. It takes as input a URL and returns a textual representation of the corresponding web page.
def fetch_page(url):
# insert your code here
b) We implement the searcher as a subclass of the IRSystem:
class WebSearcher(IRSystem):
Overwrite the method index_collection. The new method takes as input a list of URLs, fetches the textual contents for each of those URLs and adds the contents to the index.
class WebSearcher(IRSystem):
# insert your code here
Initialize your searcher and add a collection of web pages:
searcher = WebSearcher()
searcher.index_collection(["https://en.wikipedia.org/wiki/Albert_einstein",
"http://nlp.stanford.edu/IR-book/",
"http://www.crummy.com/software/BeautifulSoup/"])
Finally search for documents in the index using different queries:
searcher.present_results("soup")
searcher.present_results("retrieval")
You've reached the end of the chapter. Ignore the code below, it's just here to make the page pretty:
from IPython.core.display import HTML
def css_styling():
styles = open("styles/custom.css", "r").read()
return HTML(styles)
css_styling()

Python Programming for the Humanities by http://fbkarsdorp.github.io/python-course is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Based on a work at https://github.com/fbkarsdorp/python-course.