Basic trigonometry¶
Marcos Duarte
Laboratory of Biomechanics and Motor Control (http://demotu.org/)
Federal University of ABC, Brazil
If two right triangles (triangles with an angle of $90^o$ ($\pi/2$ radians)) have equal acute angles, they are similar, so their side lengths are proportional.
These proportionality constants are the values of $\sin\theta$, $\cos\theta$, and $\tan\theta$.
Here is a geometric representation of the main trigonometric functions of an angle $\theta$:

Radian¶
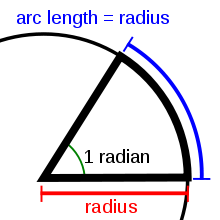
An arc of a circle with the same length as the radius of that circle corresponds to an angle of 1 radian:
Common trigonometric values¶
| $\;\theta\;(^o)$ | $\;\theta\;(rad)$ | $\;\sin \theta\;$ | $\;\cos \theta\;$ | $\;\tan \theta\;$ |
|---|---|---|---|---|
| $0^o$ | $0$ | $0$ | $1$ | $0$ |
| $30^o$ | $\pi/6$ | $1/2$ | $\sqrt{3}/2$ | $1\sqrt{3}$ |
| $45^o$ | $\pi/4$ | $\sqrt{2}/2$ | $\sqrt{2}/2$ | $1$ |
| $60^o$ | $\pi/3$ | $\sqrt{3}/2$ | $1/2$ | $\sqrt{3}$ |
| $90^o$ | $\pi/2$ | $1$ | $0$ | $\infty$ |
Trigonometric identities¶
Some of the main trigonometric identities are (see a complete list at Wikipedia):
$$ \sin^2{\alpha} + \cos^2{\alpha} = 1 $$$$ \sin(2\alpha) = 2\sin{\alpha} \cos{\alpha} $$$$ \cos(2\alpha) = \cos^2{\alpha} - \sin^2{\alpha} $$$$ \sin(\alpha \pm \beta) = \sin{\alpha} \cos{\beta} \pm \cos{\alpha} \sin{\beta} $$$$ \cos(\alpha \pm \beta) = \cos{\alpha} \cos{\beta} \mp \sin{\alpha} \cos{\beta} $$In [ ]: