Python for scientific computing¶
Marcos Duarte, Renato Naville Watanabe
Laboratory of Biomechanics and Motor Control
Federal University of ABC, Brazil
from IPython.display import Image
Image(data='http://imgs.xkcd.com/comics/python.png')
Contents
- 1 Computing as a third kind of Science
- 2 About Python [Python documentation]
- 3 About Python [Python documentation]
- 4 Glossary for the Python technical characteristics I
- 5 Glossary for the Python technical characteristics II
- 6 About Python
- 7 Python
- 8 Why Python and not 'X' (put any other language here)
- 9 Popularity of Python for teaching
- 10 Python ecosystem for scientific computing (main libraries)
- 11 The Jupyter Notebook
- 12 Jupyter Notebook and IPython kernel architectures
- 13 Installing the Python ecosystem
- 14 IDE for Python
- 15 To learn about Python
- 16 More examples of Jupyter Notebooks
- 17 Questions?
The Python programming language with its ecosystem for scientific programming has features, maturity, and a community of developers and users that makes it the ideal environment for the scientific community.
This talk will show some of these features and usage examples.
Computing as a third kind of Science¶
Traditionally, science has been divided into experimental and theoretical disciplines, but nowadays computing plays an important role in science. Scientific computation is sometimes related to theory, and at other times to experimental work. Hence, it is often seen as a new third branch of science.
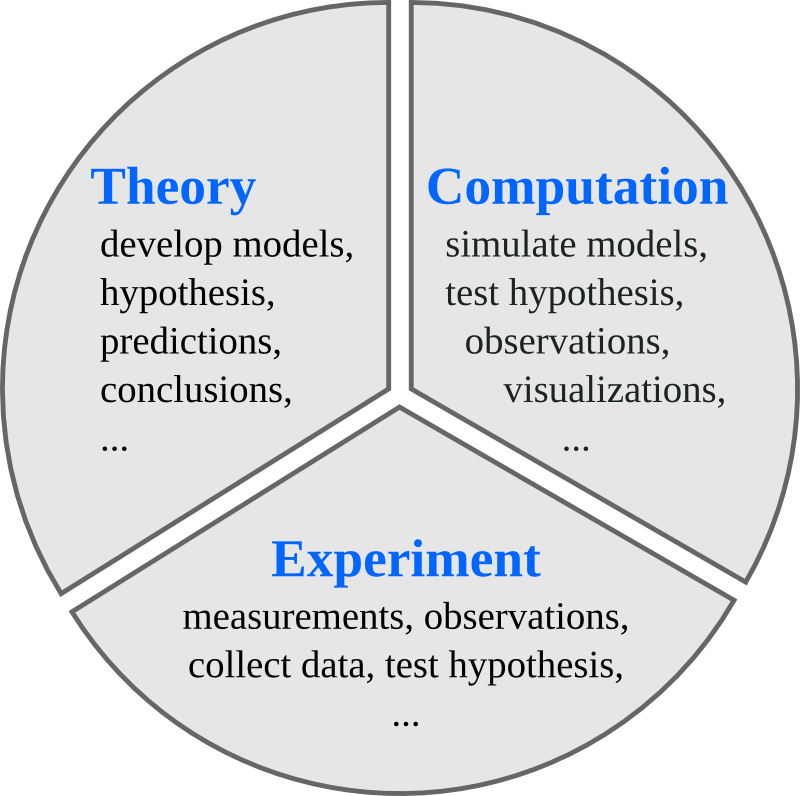
Figure from J.R. Johansson.
About Python [Python documentation]¶
Python is a programming language that lets you work more quickly and integrate your systems more effectively. You can learn to use Python and see almost immediate gains in productivity and lower maintenance costs [python.org].
- Python is an interpreted, object-oriented, high-level programming language with dynamic semantics. Its high-level built in data structures, combined with dynamic typing and dynamic binding, make it very attractive for Rapid Application Development, as well as for use as a scripting or glue language to connect existing components together.
- Python's simple, easy to learn syntax emphasizes readability and therefore reduces the cost of program maintenance. Python supports modules and packages, which encourages program modularity and code reuse.
- Python is free and open source.
About Python [Python documentation]¶
- Often, programmers fall in love with Python because of the increased productivity it provides. Since there is no compilation step, the edit-test-debug cycle is incredibly fast. Debugging Python programs is easy: a bug or bad input will never cause a segmentation fault. Instead, when the interpreter discovers an error, it raises an exception. When the program doesn't catch the exception, the interpreter prints a stack trace.
- A source level debugger allows inspection of local and global variables, evaluation of arbitrary expressions, setting breakpoints, stepping through the code a line at a time, and so on. The debugger is written in Python itself, testifying to Python's introspective power. On the other hand, often the quickest way to debug a program is to add a few print statements to the source: the fast edit-test-debug cycle makes this simple approach very effective.*
Glossary for the Python technical characteristics I¶
- Programming language: a formal language designed to communicate instructions to a computer. A sequence of instructions that specifies how to perform a computation is called a program.
- Interpreted language: a program in an interpreted language is executed or interpreted by an interpreter program. This interpreter executes the program source code, statement by statement.
- Compiled language: a program in a compiled language is first explicitly translated by the user into a lower-level machine language executable (with a compiler) and then this program can be executed.
- Python interpreter: an interpreter is the computer program that executes the program. The most-widely used implementation of the Python programming language, referred as CPython or simply Python, is written in C (another programming language, which is lower-level and compiled).
- High-level: a high-level programming language has a strong abstraction from the details of the computer and the language is independent of a particular type of computer. A high-level programming language is closer to human languages than to the programming language running inside the computer that communicate instructions to its hardware, the machine language. The machine language is a low-level programming language, in fact, the lowest one.
- Object-oriented programming: a programming paradigm that represents concepts as "objects" that have data fields (attributes that describe the object) and associated procedures known as methods.
- Semantics and syntax: the term semantics refers to the meaning of a language, as opposed to its form, the syntax.
- Static and dynamic semantics: static and dynamic refer to the point in time at which some programming element is resolved. Static indicates that resolution takes place at the time a program is written. Dynamic indicates that resolution takes place at the time a program is executed.
- Static and dynamic typing and binding: in dynamic typing, the type of the variable (e.g., if it is an integer or a string or a different type of element) is not explicitly declared, it can change, and in general is not known until execution time. In static typing, the type of the variable must be declared and it is known before the execution time.
- Rapid Application Development: a software development methodology that uses minimal planning in favor of rapid prototyping.
- Scripting: the writing of scripts, small pieces of simple instructions (programs) that can be rapidly executed.
Glossary for the Python technical characteristics II¶
- Glue language: a programming language for writing programs to connect software components (including programs written in other programming languages).
- Modules and packages: a module is a file containing Python definitions (e.g., functions) and statements. Packages are a way of structuring Python’s module namespace by using “dotted module names”. For example, the module name A.B designates a submodule named B in a package named A. To be used, modules and packages have to be imported in Python with the import function. Namespace is a container for a set of identifiers (names), and allows the disambiguation of homonym identifiers residing in different namespaces. For example, with the command
import math, we will have all the functions and statements defined in this module in the namespace 'math.', for example,math.piis the $\pi$ constant andmath.cos(), the cosine function. - Program modularity and code reuse: the degree that programs can be compartmentalized (divided in smaller programs) to facilitate program reuse.
- Source or binary form: source refers to the original code of the program (typically in a text format) which would need to be compiled to a binary form (not anymore human readable) to be able to be executed.
- Major platforms: typically refers to the main operating systems (OS) in the market: Windows (by Microsoft), Mac OSX (by Apple), and Linux distributions (such as Debian, Ubuntu, Mint, etc.). Mac OSX and Linux distros are derived from, or heavily inspired by, another operating system called Unix.
- Edit-test-debug cycle: the typical cycle in the life of a programmer; write (edit) the code, run (test) it, and correct errors or improve it (debug). The read–eval–print loop (REPL) is another related term.
- Segmentation fault: an error in a program that is generated by the hardware which notifies the operating system about a memory access violation.
- Exception: an error in a program detected during execution is called an exception and the Python interpreter raises a message about this error (an exception is not necessarily fatal, i.e., does not necessarily terminate or break the program).
- Stack trace: information related to what caused the exception describing the line of the program where it occurred with a possible history of related events.
- Source level debugger: Python has a module (named pdb) for interactive source code debugging.
- Local and global variables: refers to the scope of the variables. A local variable is defined inside a function and typically can be accessed (it exists) only inside that function unless declared as global.
About Python¶
Python is also the name of the software with the most-widely used implementation of the language (maintained by the Python Software Foundation).
This implementation is written mostly in the C programming language and it is nicknamed CPython.
So, the following phrase is correct: download Python (the software) to program in Python (the language) because Python (both) is great!
Python¶
The origin of the name for the Python language in fact is not because of the big snake, the author of the Python language, Guido van Rossum, named the language after Monty Python, a famous British comedy group in the 70's.
By coincidence, the Monty Python group was also interested in human movement science:
from IPython.display import YouTubeVideo
YouTubeVideo('eCLp7zodUiI', width=480, height=360, rel=0)
Why Python and not 'X' (put any other language here)¶
Python is not the best programming language for all needs and for all people. There is no such language.
Now, if you are doing scientific computing, chances are that Python is perfect for you because (and might also be perfect for lots of other needs):
- Python is free, open source, and cross-platform.
- Python is easy to learn, with readable code, well documented, and with a huge and friendly user community.
- Python is a real programming language, able to handle a variety of problems, easy to scale from small to huge problems, and easy to integrate with other systems (including other programming languages).
- Python code is not the fastest but Python is one the fastest languages for programming. It is not uncommon in science to care more about the time we spend programming than the time the program took to run. But if code speed is important, one can easily integrate in different ways a code written in other languages (such as C and Fortran) with Python.
- The Jupyter Notebook is a versatile tool for programming, data visualization, plotting, simulation, numeric and symbolic mathematics, and writing for daily use.
Popularity of Python for teaching¶
from IPython.display import IFrame
IFrame('https://cacm.acm.org/blogs/blog-cacm/176450-python-is-now-the-most-popular-introductory-teaching-language-at-top-us-universities/fulltext',
width=800, height=600)
Python ecosystem for scientific computing (main libraries)¶
- Python of course (the CPython distribution): a free, open source and cross-platform programming language that lets you work more quickly and integrate your systems more effectively.
- Numpy: fundamental package for scientific computing with a N-dimensional array package.
- Scipy: numerical routines for scientific computing.
- Matplotlib: comprehensive 2D Plotting.
- Sympy: symbolic mathematics.
- Pandas: data structures and data analysis tools.
- IPython: provides a rich architecture for interactive computing with powerful interactive shell, kernel for Jupyter, support for interactive data visualization and use of GUI toolkits, flexible embeddable interpreters, and high performance tools for parallel computing.
- Jupyter Notebook: web application that allows you to create and share documents that contain live code, equations, visualizations and explanatory text.
- Statsmodels: to explore data, estimate statistical models, and perform statistical tests.
- Scikit-learn: tools for data mining and data analysis (including machine learning).
- Pillow: Python Imaging Library.
- Spyder: interactive development environment with advanced editing, interactive testing, debugging and introspection features.
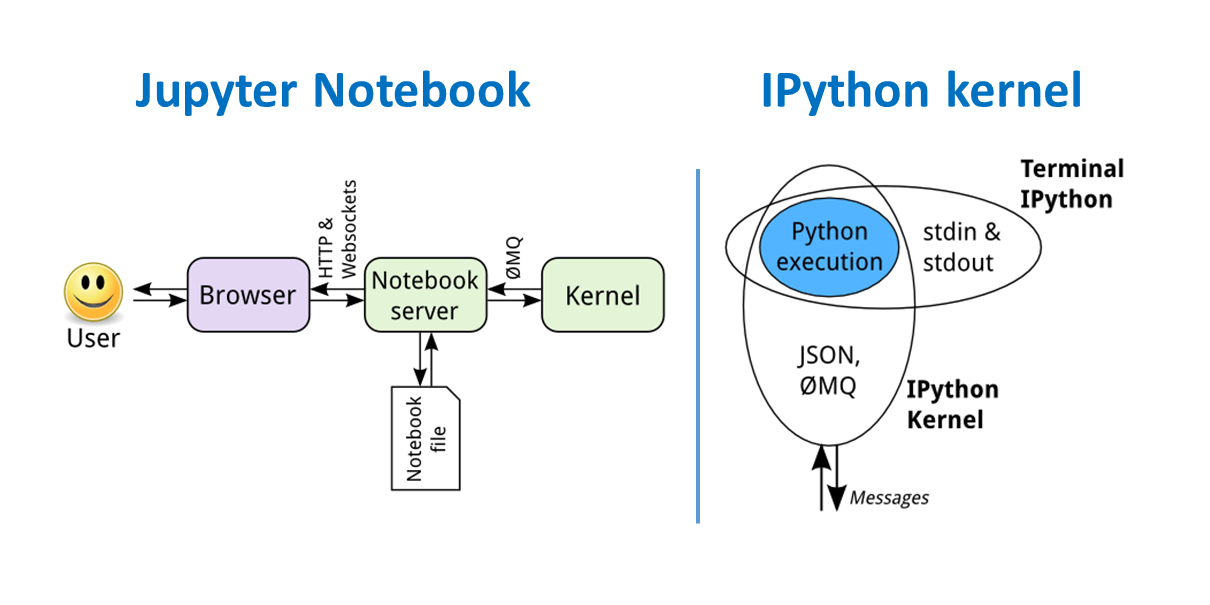
The Jupyter Notebook¶
The Jupyter Notebook App is a server-client application that allows editing and running notebook documents via a web browser. The Jupyter Notebook App can be executed on a local desktop requiring no Internet access (as described in this document) or installed on a remote server and accessed through the Internet.
Notebook documents (or “notebooks”, all lower case) are documents produced by the Jupyter Notebook App which contain both computer code (e.g. python) and rich text elements (paragraph, equations, figures, links, etc...). Notebook documents are both human-readable documents containing the analysis description and the results (figures, tables, etc..) as well as executable documents which can be run to perform data analysis.
Jupyter Notebook and IPython kernel architectures¶
Installing the Python ecosystem¶
The easy way
The easiest way to get Python and the most popular packages for scientific programming is to install them with a Python distribution such as Anaconda or Miniconda.
In fact, you don't even need to install Python in your computer, you can run Python for scientific programming in the cloud using python.org, Google Colaboratory, or repl.it.
The hard way
You can download Python and all individual packages you need and install them one by one. In general, it's not that difficult, but it can become challenging and painful for certain big packages heavily dependent on math, image visualization, and your operating system (i.e., Microsoft Windows).
Anaconda¶
Go to the Anaconda website and download the appropriate version for your computer (but download Anaconda3! for Python 3.x). The file is big (about 500 MB).
Follow the installation steps described in the Anaconda documentatione for your operational system.
My current installation¶
import sys
sys.version
'3.9.13 | packaged by conda-forge | (main, May 27 2022, 16:56:21) \n[GCC 10.3.0]'
More information can be obtained using the watermark extension:
# !pip install watermark
from watermark import watermark
print(watermark())
Last updated: 2022-09-20T01:01:15.342069-03:00 Python implementation: CPython Python version : 3.9.13 IPython version : 7.33.0 Compiler : GCC 10.3.0 OS : Linux Release : 5.15.0-47-generic Machine : x86_64 Processor : x86_64 CPU cores : 16 Architecture: 64bit
IDE for Python¶
You might want an Integrated Development Environment (IDE) for programming in Python.
See Top Python IDEs For Data Science for possible IDEs.
Soon there will be a new IDE for scientific computing with Python: JupyterLab, developed by the Jupyter team. See this video about JupyterLab.
To learn about Python¶
There is a lot of good material in the Internet about Python for scientific computing, some of them are:
- How To Think Like A Computer Scientist or the interactive edition (book)
- Python Scientific Lecture Notes (lecture notes)
- A Whirlwind Tour of Python (tutorial/book)
- Python Data Science Handbook (tutorial/book)
More examples of Jupyter Notebooks¶
Let's run stuff from:
import this
The Zen of Python, by Tim Peters Beautiful is better than ugly. Explicit is better than implicit. Simple is better than complex. Complex is better than complicated. Flat is better than nested. Sparse is better than dense. Readability counts. Special cases aren't special enough to break the rules. Although practicality beats purity. Errors should never pass silently. Unless explicitly silenced. In the face of ambiguity, refuse the temptation to guess. There should be one-- and preferably only one --obvious way to do it. Although that way may not be obvious at first unless you're Dutch. Now is better than never. Although never is often better than *right* now. If the implementation is hard to explain, it's a bad idea. If the implementation is easy to explain, it may be a good idea. Namespaces are one honking great idea -- let's do more of those!