Muscle simulation¶
Marcos Duarte, Renato Watanabe
Laboratory of Biomechanics and Motor Control
Federal University of ABC, Brazil
Let's simulate the 3-component Hill-type muscle model we described in Muscle modeling and illustrated below:
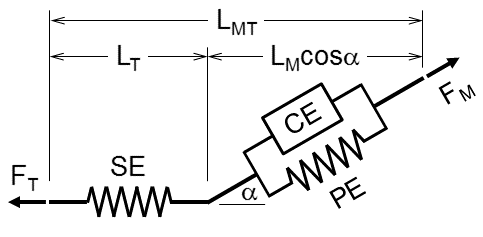
If we assume that the muscle–tendon system is at equilibrium, that is, muscle, $F_{M}$, and tendon, $F_{T}$, forces are in equilibrium at all times, the following equation holds (and that a muscle can only pull):
\begin{equation} F_{T} = F_{SE} = F_{M}\cos\alpha \label{} \end{equation}Pennation angle¶
The pennation angle will vary during muscle activation; for instance, Kawakami et al. (1998) showed that the pennation angle of the medial gastrocnemius muscle can vary from 22$^o$ to 67$^o$ during activation. The most used approach is to assume that the muscle width (defined as the length of the perpendicular line between the lines of the muscle origin and insertion) remains constant (Scott & Winter, 1991):
\begin{equation} w = L_{M,0} \sin\alpha_0 \label{} \end{equation}The pennation angle as a function of time will be given by:
\begin{equation} \alpha = \sin^{-1} \left(\dfrac{w}{L_M}\right) \label{} \end{equation}The cosine of the pennation angle can be given by (if $L_M$ is known):
\begin{equation} \cos \alpha = \dfrac{\sqrt{L_M^2-w^2}}{L_M} = \sqrt{1-\left(\dfrac{w}{L_M}\right)^2} \label{} \end{equation}or (if $L_M$ is not known):
\begin{equation} \cos \alpha = \dfrac{L_{MT}-L_T}{L_M} = \dfrac{1}{\sqrt{1 + \left(\dfrac{w}{L_{MT}-L_T}\right)^2}} \label{} \end{equation}Muscle force¶
In general, the dependence of the force of the contractile element with its length and velocity and with the activation level are assumed independent of each other:
\begin{equation} F_{CE}(a, L_{CE}, \dot{L}_{CE}) = a \: f_l(L_{CE}) \: f_v(\dot{L}_{CE}) \: F_{M0} \label{} \end{equation}where $f_l(L_M)$ and $f_v(\dot{L}_M)$ are mathematical functions describing the force-length and force-velocity relationships of the contractile element (typically these functions are normalized by $F_{M0}$, the maximum isometric (at zero velocity) muscle force, so we have to multiply the right side of the equation by $F_{M0}$).
And for the muscle force:
\begin{equation} F_{M}(a, L_M, \dot{L}_M) = \left[a \: f_l(L_M)f_v(\dot{L}_M) + F_{PE}(L_M)\right]F_{M0} \label{} \end{equation}This equation for the muscle force, with $a$, $L_{M}$, and $\dot{L}_{M}$ as state variables, can be used to simulate the dynamics of a muscle given an excitation and determine the muscle force and length. We can rearrange the equation, invert the expression for $f_v$, and integrate the resulting first-order ordinary differential equation (ODE) to obatin $L_M$:
\begin{equation} \dot{L}_M = f_v^{-1}\left(\dfrac{F_{SE}(L_{MT}-L_M\cos\alpha)/\cos\alpha - F_{PE}(L_M)}{a f_l(L_M)}\right) \label{} \end{equation}This approach is the most commonly employed in the literature (see for example, OpenSim; McLean, Su, van den Bogert, 2003; Thelen, 2003; Nigg and Herzog, 2007).
Although the equation for the muscle force doesn't have numerical singularities, the differential equation for muscle velocity has four (OpenSim Millard 2012 Muscle Models):
When $a \rightarrow 0$; when $f_l(L_M) \rightarrow 0$; when $\alpha \rightarrow \pi/2$; and when $\partial f_v/\partial v \rightarrow 0 $.
The following solutions can be employed to avoid the numerical singularities (OpenSim Millard 2012 Muscle Models):
- A minimum value for $a$; e.g., $a_{min}=0.01$;
- A minimum value for $f_l(L_M)$; e.g., $f_l(0.1)$;
- A maximum value for pennation angle; e.g., constrain $\alpha$ to $\cos\alpha > 0.1; (\alpha < 84.26^o)$;
- Make the slope of $f_V$ at and beyond maximum velocity different than zero (for both concentric and eccentric activations).
We will adopt these solutions to avoid singularities in the simulation of muscle mechanics. A problem of imposing values to variables as described above is that we can make the ordinary differential equation numerically stiff, which will increase the computational cost of the numerical integration. A better solution would be to modify the model to not have these singularities (see OpenSim Millard 2012 Muscle Models).
Simulation¶
Let's simulate muscle dynamics using the Thelen2003Muscle model we defined in Muscle modeling. For the simulation of the Thelen2003Muscle, we simply have to integrate the equation:
\begin{equation} V_M = (0.25+0.75a)\,V_{Mmax}\frac{\bar{F}_M-a\bar{f}_{l,CE}}{b} \label{} \end{equation}where
\begin{equation} b = \left\{ \begin{array}{l l l} a\bar{f}_{l,CE} + \bar{F}_M/A_f \quad & \text{if} \quad \bar{F}_M \leq a\bar{f}_{l,CE} & \text{(shortening)} \\ \\ \dfrac{(2+2/A_f)(a\bar{f}_{l,CE}\bar{f}_{CEmax} - \bar{F}_M)}{\bar{f}_{CEmax}-1} \quad & \text{if} \quad \bar{F}_M > a\bar{f}_{l,CE} & \text{(lengthening)} \end{array} \right. \label{} \end{equation}The equation above already contains the terms for actvation, $a$, and force-length dependence, $\bar{f}_{l,CE}$. The equation is too complicated for solving analytically, we will solve it by numerical integration using the scipy.integrate.ode class of numeric integrators, particularly the dopri5, an explicit runge-kutta method of order (4)5 due to Dormand and Prince (a.k.a. ode45 in Matlab). We could run a simulation using OpenSim; it would be faster, but for fun, let's program in Python. All the necessary functions for the Thelen2003Muscle model described in Muscle modeling were grouped in one file (module), muscles.py. Besides these functions, the module muscles.py contains a function for the muscle velocity, vm_eq, which will be called by the function that specifies the numerical integration, lm_sol; a standard way of performing numerical integration in scientific computing:
def vm_eq(self, t, lm, lm0, lmt0, lmopt, ltslack, alpha0, vmmax, fm0):
"""Equation for muscle velocity."""
if lm < 0.1*lmopt:
lm = 0.1*lmopt
a = self.activation(t)
lmt = self.lmt_eq(t, lmt0)
alpha = self.penn_ang(lmt=lmt, lm=lm, lm0=lm0, alpha0=alpha0)
lt = lmt - lm*np.cos(alpha)
fse = self.force_se(lt=lt, ltslack=ltslack)
fpe = self.force_pe(lm=lm/lmopt)
fl = self.force_l(lm=lm/lmopt)
fce_t = fse/np.cos(alpha) - fpe
vm = self.velo_fm(fm=fce_t, a=a, fl=fl)
return vm
def lm_sol(self, fun, t0, t1, lm0, lmt0, ltslack, lmopt, alpha0, vmmax, fm0, show, axs):
"""Runge-Kutta (4)5 ODE solver for muscle length."""
if fun is None:
fun = self.vm_eq
f = ode(fun).set_integrator('dopri5', nsteps=1, max_step=0.005, atol=1e-8)
f.set_initial_value(lm0, t0).set_f_params(lm0, lmt0, lmopt, ltslack, alpha0, vmmax, fm0)
# suppress Fortran warning
warnings.filterwarnings("ignore", category=UserWarning)
data = []
while f.t < t1:
f.integrate(t1, step=True)
d = self.calc_data(f.t, f.y[0], lm0, lmt0, ltslack, lmopt, alpha0, fm0)
data.append(d)
warnings.resetwarnings()
data = np.array(data)
self.lm_data = data
if show:
self.lm_plot(data, axs)
return data
muscles.py also contains some auxiliary functions for entering data and for plotting the results. Let's import the necessary Python libraries and customize the environment in order to run some simulations using muscles.py:
import numpy as np
%matplotlib notebook
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['lines.linewidth'] = 2
matplotlib.rcParams['font.size'] = 12
matplotlib.rcParams['lines.markersize'] = 4
matplotlib.rc('axes', grid=True, labelsize=12, titlesize=13, ymargin=0.01)
matplotlib.rc('legend', numpoints=1, fontsize=10)
# import the muscles.py module
import sys
sys.path.insert(1, r'./../functions')
import muscles
The muscles.py module contains the class Thelen2003() which has the functions we want to use. For such, we need to create an instance of this class:
ms = muscles.Thelen2003()
Now, we need to enter the parameters and states for the simulation: we can load files with these values or enter as input parameters when calling the function (method) 'set_parameters()' and 'set_states()'. If nothing if inputed, these methods assume that the parameters and states are stored in the files 'muscle_parameter.txt' and 'muscle_state.txt' inside the directory './../data/'. Let's use some of the parameters and states from an exercise of the chapter 4 of Nigg and Herzog (2006).
ms.set_parameters()
ms.set_states()
The parameters were successfully loaded and are stored in the variable P. The states were successfully loaded and are stored in the variable S.
We can see the parameters and states:
print('Parameters:\n', ms.P)
print('States:\n', ms.S)
Parameters:
{'id': '', 'name': '', 'u_max': 1.0, 'u_min': 0.01, 't_act': 0.015, 't_deact': 0.05, 'lmopt': 0.093, 'alpha0': 0.0, 'fm0': 7400.0, 'gammal': 0.45, 'kpe': 5.0, 'epsm0': 0.6, 'vmmax': 10.0, 'fmlen': 1.4, 'af': 0.25, 'ltslack': 0.223, 'epst0': 0.04, 'kttoe': 3.0}
States:
{'id': '', 'name': '', 'lmt0': 0.31, 'lm0': 0.087, 'lt0': 0.223}
We can plot the muscle-tendon forces considering these parameters and initial states:
ms.muscle_plot();
Let's simulate an isometric activation (and since we didn't enter an activation level, $a=1$ will be used):
def lmt_eq(t, lmt0):
# isometric activation
lmt = lmt0
return lmt
ms.lmt_eq = lmt_eq
data = ms.lm_sol()
We can input a prescribed muscle-tendon length for the simulation:
def lmt_eq(t, lmt0):
# prescribed change in the muscle-tendon length
if t < 1:
lmt = lmt0
if 1 <= t < 2:
lmt = lmt0 - 0.04*(t - 1)
if t >= 2:
lmt = lmt0 - 0.04
return lmt
ms.lmt_eq = lmt_eq
data = ms.lm_sol()
Let's simulate a pennated muscle with an angle of $30^o$. We don't need to enter all parameters again, we can change only the parameter alpha0:
ms.P['alpha0'] = 30*np.pi/180
print('New initial pennation angle:', ms.P['alpha0'])
New initial pennation angle: 0.5235987755982988
Because the muscle length is now shortened by $\cos(30^o)$, we will also have to change the initial muscle-tendon length if we want to start with the tendon at its slack length:
ms.S['lmt0'] = ms.S['lmt0'] - ms.S['lm0'] + ms.S['lm0']*np.cos(ms.P['alpha0'])
print('New initial muscle-tendon length:', ms.S['lmt0'])
New initial muscle-tendon length: 0.29834421012924617
data = ms.lm_sol()
Here is a plot of the simulated pennation angle:
plt.figure(figsize=(7, 4))
plt.plot(data[:, 0], data[:, 9]*180/np.pi)
plt.xlabel('Time (s)')
plt.ylabel(r'Pennation angle $(^o)$')
plt.show()
Change back to the old values:
ms.P['alpha0'] = 0
ms.S['lmt0'] = 0.313
We can change the initial states to show the role of the passive parallel element:
ms.S = {'id': '', 'lt0': np.nan, 'lmt0': 0.323, 'lm0': 0.10, 'name': ''}
ms.muscle_plot();
Let's also change the excitation signal:
def excitation(t, u_max=1, u_min=0.01, t0=1, t1=2):
"""Excitation signal, a hat signal."""
u = u_min
if t >= t0 and t <= t1:
u = u_max
return u
ms.excitation = excitation
act = ms.activation_sol()
And let's simulate an isometric contraction:
def lmt_eq(t, lmt0):
# isometric activation
lmt = lmt0
return lmt
ms.lmt_eq = lmt_eq
data = ms.lm_sol()
Let's use as excitation a train of pulses:
def excitation(t, u_max=.5, u_min=0.01, t0=.2, t1=2):
"""Excitation signal, a train of square pulses."""
u = u_min
ts = np.arange(1, 2.0, .1)
#ts = np.delete(ts, np.arange(2, ts.size, 3))
if t >= ts[0] and t <= ts[1]:
u = u_max
elif t >= ts[2] and t <= ts[3]:
u = u_max
elif t >= ts[4] and t <= ts[5]:
u = u_max
elif t >= ts[6] and t <= ts[7]:
u = u_max
elif t >= ts[8] and t <= ts[9]:
u = u_max
return u
ms.excitation = excitation
act = ms.activation_sol()
data = ms.lm_sol()
References¶
- Kawakami Y, Ichinose Y, Fukunaga T (1998) Architectural and functional features of human triceps surae muscles during contraction. Journal of Applied Physiology, 85, 398–404.
- McLean SG, Su A, van den Bogert AJ (2003) Development and validation of a 3-D model to predict knee joint loading during dynamic movement. Journal of Biomechanical Engineering, 125, 864-74.
- Nigg BM and Herzog W (2006) Biomechanics of the Musculo-skeletal System. 3rd Edition. Wiley.
- Scott SH, Winter DA (1991) A comparison of three muscle pennation assumptions and their effect on isometric and isotonic force. Journal of Biomechanics, 24, 163–167.
- Thelen DG (2003) Adjustment of muscle mechanics model parameters to simulate dynamic contractions in older adults. Journal of Biomechanical Engineering, 125(1):70–77.
Module muscles.py¶
# %load ./../functions/muscles.py
"""Muscle modeling and simulation."""
import numpy as np
from scipy.integrate import ode
import warnings
import configparser
__author__ = 'Marcos Duarte, https://github.com/BMClab/BMC'
__version__ = 'muscles.py v.1.01 2021/07/15'
class Thelen2003():
""" Thelen (2003) muscle model.
"""
def __init__(self, parameters=None, states=None):
if parameters is not None:
self.set_parameters(parameters)
if states is not None:
self.set_states(states)
self.lm_data = []
self.act_data = []
def set_parameters(self, var=None):
"""Load and set parameters for the muscle model.
"""
if var is None:
var = './../data/muscle_parameter.txt'
if isinstance(var, str):
self.P = self.config_parser(var, 'parameters')
elif isinstance(var, dict):
self.P = var
else:
raise ValueError('Wrong parameters!')
print('The parameters were successfully loaded ' +
'and are stored in the variable P.')
def set_states(self, var=None):
"""Load and set states for the muscle model.
"""
if var is None:
var = './../data/muscle_state.txt'
if isinstance(var, str):
self.S = self.config_parser(var, 'states')
elif isinstance(var, dict):
self.S = var
else:
raise ValueError('Wrong states!')
print('The states were successfully loaded ' +
'and are stored in the variable S.')
def config_parser(self, filename, var):
parser = configparser.ConfigParser()
parser.optionxform = str # make option names case sensitive
parser.read(filename)
if not parser:
raise ValueError('File %s not found!' %var)
#if not 'Muscle' in parser.sections()[0]:
# raise ValueError('Wrong %s file!' %var)
var = {}
for key, value in parser.items(parser.sections()[0]):
if key.lower() in ['name', 'id']:
var.update({key: value})
else:
try:
value = float(value)
except ValueError:
print('"%s" value "%s" was replaced by NaN.' %(key, value))
value = np.nan
var.update({key: value})
return var
def force_l(self, lm, gammal=None):
"""Thelen (2003) force of the contractile element vs. muscle length.
Parameters
----------
lm : float
normalized muscle fiber length
gammal : float, optional (default from parameter file)
shape factor
Returns
-------
fl : float
normalized force of the muscle contractile element
"""
if gammal is None: gammal = self.P['gammal']
fl = np.exp(-(lm-1)**2/gammal)
return fl
def force_pe(self, lm, kpe=None, epsm0=None):
"""Thelen (2003) force of the muscle parallel element vs. muscle length.
Parameters
----------
lm : float
normalized muscle fiber length
kpe : float, optional (default from parameter file)
exponential shape factor
epsm0 : float, optional (default from parameter file)
passive muscle strain due to maximum isometric force
Returns
-------
fpe : float
normalized force of the muscle parallel (passive) element
"""
if kpe is None: kpe = self.P['kpe']
if epsm0 is None: epsm0 = self.P['epsm0']
if lm <= 1:
fpe = 0
else:
fpe = (np.exp(kpe*(lm-1)/epsm0)-1)/(np.exp(kpe)-1)
return fpe
def force_se(self, lt, ltslack=None, epst0=None, kttoe=None):
"""Thelen (2003) force-length relationship of tendon vs. tendon length.
Parameters
----------
lt : float
tendon length (normalized or not)
ltslack : float, optional (default from parameter file)
tendon slack length (normalized or not)
epst0 : float, optional (default from parameter file)
tendon strain at the maximal isometric muscle force
kttoe : float, optional (default from parameter file)
linear scale factor
Returns
-------
fse : float
normalized force of the tendon series element
"""
if ltslack is None: ltslack = self.P['ltslack']
if epst0 is None: epst0 = self.P['epst0']
if kttoe is None: kttoe = self.P['kttoe']
epst = (lt-ltslack)/ltslack
fttoe = .33
# values from OpenSim Thelen2003Muscle
epsttoe = .99*epst0*np.e**3/(1.66*np.e**3 - .67)
ktlin = .67/(epst0 - epsttoe)
#
if epst <= 0:
fse = 0
elif epst <= epsttoe:
fse = fttoe/(np.exp(kttoe)-1)*(np.exp(kttoe*epst/epsttoe)-1)
else:
fse = ktlin*(epst-epsttoe) + fttoe
return fse
def velo_fm(self, fm, a, fl, lmopt=None, vmmax=None, fmlen=None, af=None):
"""Thelen (2003) velocity of the force-velocity relationship vs. CE force.
Parameters
----------
fm : float
normalized muscle force
a : float
muscle activation level
fl : float
normalized muscle force due to the force-length relationship
lmopt : float, optional (default from parameter file)
optimal muscle fiber length
vmmax : float, optional (default from parameter file)
normalized maximum muscle velocity for concentric activation
fmlen : float, optional (default from parameter file)
normalized maximum force generated at the lengthening phase
af : float, optional (default from parameter file)
shape factor
Returns
-------
vm : float
velocity of the muscle
"""
if lmopt is None: lmopt = self.P['lmopt']
if vmmax is None: vmmax = self.P['vmmax']
if fmlen is None: fmlen = self.P['fmlen']
if af is None: af = self.P['af']
if fm <= a*fl: # isometric and concentric activation
if fm > 0:
b = a*fl + fm/af
else:
b = a*fl
else: # eccentric activation
asyE_thresh = 0.95 # from OpenSim Thelen2003Muscle
if fm < a*fl*fmlen*asyE_thresh:
b = (2 + 2/af)*(a*fl*fmlen - fm)/(fmlen - 1)
else:
fm0 = a*fl*fmlen*asyE_thresh
b = (2 + 2/af)*(a*fl*fmlen - fm0)/(fmlen - 1)
vm = (0.25 + 0.75*a)*1*(fm - a*fl)/b
vm = vm*vmmax*lmopt
return vm
def force_vm(self, vm, a, fl, lmopt=None, vmmax=None, fmlen=None, af=None):
"""Thelen (2003) force of the contractile element vs. muscle velocity.
Parameters
----------
vm : float
muscle velocity
a : float
muscle activation level
fl : float
normalized muscle force due to the force-length relationship
lmopt : float, optional (default from parameter file)
optimal muscle fiber length
vmmax : float, optional (default from parameter file)
normalized maximum muscle velocity for concentric activation
fmlen : float, optional (default from parameter file)
normalized normalized maximum force generated at the lengthening phase
af : float, optional (default from parameter file)
shape factor
Returns
-------
fvm : float
normalized force of the muscle contractile element
"""
if lmopt is None: lmopt = self.P['lmopt']
if vmmax is None: vmmax = self.P['vmmax']
if fmlen is None: fmlen = self.P['fmlen']
if af is None: af = self.P['af']
vmmax = vmmax*lmopt
if vm <= 0: # isometric and concentric activation
fvm = af*a*fl*(4*vm + vmmax*(3*a + 1))/(-4*vm + vmmax*af*(3*a + 1))
else: # eccentric activation
fvm = a*fl*(af*vmmax*(3*a*fmlen - 3*a + fmlen - 1) + \
8*vm*fmlen*(af + 1)) / \
(af*vmmax*(3*a*fmlen - 3*a + fmlen - 1) + 8*vm*(af + 1))
return fvm
def lmt_eq(self, t, lmt0=None):
"""Equation for muscle-tendon length."""
if lmt0 is None:
lmt0 = self.S['lmt0']
return lmt0
def vm_eq(self, t, lm, lm0, lmt0, lmopt, ltslack, alpha0, vmmax, fm0):
"""Equation for muscle velocity."""
if lm < 0.1*lmopt:
lm = 0.1*lmopt
#lt0 = lmt0 - lm0*np.cos(alpha0)
a = self.activation(t)
lmt = self.lmt_eq(t, lmt0)
alpha = self.penn_ang(lmt=lmt, lm=lm, lm0=lm0, alpha0=alpha0)
lt = lmt - lm*np.cos(alpha)
fse = self.force_se(lt=lt, ltslack=ltslack)
fpe = self.force_pe(lm=lm/lmopt)
fl = self.force_l(lm=lm/lmopt)
fce_t = fse/np.cos(alpha) - fpe
#if fce_t < 0: fce_t=0
vm = self.velo_fm(fm=fce_t, a=a, fl=fl)
return vm
def lm_sol(self, fun=None, t0=0, t1=3, lm0=None, lmt0=None, ltslack=None, lmopt=None,
alpha0=None, vmmax=None, fm0=None, show=True, axs=None):
"""Runge-Kutta (4)5 ODE solver for muscle length."""
if lm0 is None: lm0 = self.S['lm0']
if lmt0 is None: lmt0 = self.S['lmt0']
if ltslack is None: ltslack = self.P['ltslack']
if alpha0 is None: alpha0 = self.P['alpha0']
if lmopt is None: lmopt = self.P['lmopt']
if vmmax is None: vmmax = self.P['vmmax']
if fm0 is None: fm0 = self.P['fm0']
if fun is None:
fun = self.vm_eq
f = ode(fun).set_integrator('dopri5', nsteps=1, max_step=0.005, atol=1e-8)
f.set_initial_value(lm0, t0).set_f_params(lm0, lmt0, lmopt, ltslack, alpha0, vmmax, fm0)
# suppress Fortran warning
warnings.filterwarnings("ignore", category=UserWarning)
data = []
while f.t < t1:
f.integrate(t1, step=True)
d = self.calc_data(f.t, np.max([f.y[0], 0.1*lmopt]), lm0, lmt0,
ltslack, lmopt, alpha0, fm0)
data.append(d)
warnings.resetwarnings()
data = np.array(data)
self.lm_data = data
if show:
self.lm_plot(data, axs)
return data
def calc_data(self, t, lm, lm0, lmt0, ltslack, lmopt, alpha0, fm0):
"""Calculus of muscle-tendon variables."""
a = self.activation(t)
lmt = self.lmt_eq(t, lmt0=lmt0)
alpha = self.penn_ang(lmt=lmt, lm=lm, lm0=lm0, alpha0=alpha0)
lt = lmt - lm*np.cos(alpha)
fl = self.force_l(lm=lm/lmopt)
fpe = self.force_pe(lm=lm/lmopt)
fse = self.force_se(lt=lt, ltslack=ltslack)
fce_t = fse/np.cos(alpha) - fpe
vm = self.velo_fm(fm=fce_t, a=a, fl=fl, lmopt=lmopt)
fm = self.force_vm(vm=vm, fl=fl, lmopt=lmopt, a=a) + fpe
data = [t, lmt, lm, lt, vm, fm*fm0, fse*fm0, a*fl*fm0, fpe*fm0, alpha]
return data
def muscle_plot(self, a=1, axs=None):
"""Plot muscle-tendon relationships with length and velocity."""
try:
import matplotlib.pyplot as plt
except ImportError:
print('matplotlib is not available.')
return
if axs is None:
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(9, 4))
lmopt = self.P['lmopt']
ltslack = self.P['ltslack']
vmmax = self.P['vmmax']
alpha0 = self.P['alpha0']
fm0 = self.P['fm0']
lm0 = self.S['lm0']
lmt0 = self.S['lmt0']
lt0 = self.S['lt0']
if np.isnan(lt0):
lt0 = lmt0 - lm0*np.cos(alpha0)
lm = np.linspace(0, 2, 101)
lt = np.linspace(0, 1, 101)*0.05 + 1
vm = np.linspace(-1, 1, 101)*vmmax*lmopt
fl = np.zeros(lm.size)
fpe = np.zeros(lm.size)
fse = np.zeros(lt.size)
fvm = np.zeros(vm.size)
fl_lm0 = self.force_l(lm0/lmopt)
fpe_lm0 = self.force_pe(lm0/lmopt)
fm_lm0 = fl_lm0 + fpe_lm0
ft_lt0 = self.force_se(lt0, ltslack)*fm0
for i in range(101):
fl[i] = self.force_l(lm[i])
fpe[i] = self.force_pe(lm[i])
fse[i] = self.force_se(lt[i], ltslack=1)
fvm[i] = self.force_vm(vm[i], a=a, fl=fl_lm0)
lm = lm*lmopt
lt = lt*ltslack
fl = fl
fpe = fpe
fse = fse*fm0
fvm = fvm*fm0
xlim = self.margins(lm, margin=.05, minmargin=False)
axs[0].set_xlim(xlim)
ylim = self.margins([0, 2], margin=.05)
axs[0].set_ylim(ylim)
axs[0].plot(lm, fl, 'b', label='Active')
axs[0].plot(lm, fpe, 'b--', label='Passive')
axs[0].plot(lm, fl+fpe, 'b:', label='')
axs[0].plot([lm0, lm0], [ylim[0], fm_lm0], 'k:', lw=2, label='')
axs[0].plot([xlim[0], lm0], [fm_lm0, fm_lm0], 'k:', lw=2, label='')
axs[0].plot(lm0, fm_lm0, 'o', ms=6, mfc='r', mec='r', mew=2, label='fl(LM0)')
axs[0].legend(loc='best', frameon=True, framealpha=.5)
axs[0].set_xlabel('Length [m]')
axs[0].set_ylabel('Scale factor')
axs[0].xaxis.set_major_locator(plt.MaxNLocator(4))
axs[0].yaxis.set_major_locator(plt.MaxNLocator(4))
axs[0].set_title('Muscle F-L (a=1)')
xlim = self.margins([0, np.min(vm), np.max(vm)], margin=.05, minmargin=False)
axs[1].set_xlim(xlim)
ylim = self.margins([0, fm0*1.2, np.max(fvm)*1.5], margin=.025)
axs[1].set_ylim(ylim)
axs[1].plot(vm, fvm, label='')
axs[1].set_xlabel(r'$\mathbf{^{CON}}\;$ Velocity [m/s] $\;\mathbf{^{EXC}}$')
axs[1].plot([0, 0], [ylim[0], fvm[50]], 'k:', lw=2, label='')
axs[1].plot([xlim[0], 0], [fvm[50], fvm[50]], 'k:', lw=2, label='')
axs[1].plot(0, fvm[50], 'o', ms=6, mfc='r', mec='r', mew=2, label='FM0(LM0)')
axs[1].plot(xlim[0], fm0, '+', ms=10, mfc='r', mec='r', mew=2, label='')
axs[1].text(vm[0], fm0, 'FM0')
axs[1].legend(loc='upper right', frameon=True, framealpha=.5)
axs[1].set_ylabel('Force [N]')
axs[1].xaxis.set_major_locator(plt.MaxNLocator(4))
axs[1].yaxis.set_major_locator(plt.MaxNLocator(4))
axs[1].set_title('Muscle F-V (a=1)')
xlim = self.margins([lt0, ltslack, np.min(lt), np.max(lt)], margin=.05,
minmargin=False)
axs[2].set_xlim(xlim)
ylim = self.margins([ft_lt0, 0, np.max(fse)], margin=.05)
axs[2].set_ylim(ylim)
axs[2].plot(lt, fse, label='')
axs[2].set_xlabel('Length [m]')
axs[2].plot([lt0, lt0], [ylim[0], ft_lt0], 'k:', lw=2, label='')
axs[2].plot([xlim[0], lt0], [ft_lt0, ft_lt0], 'k:', lw=2, label='')
axs[2].plot(lt0, ft_lt0, 'o', ms=6, mfc='r', mec='r', mew=2, label='FT(LT0)')
axs[2].legend(loc='upper left', frameon=True, framealpha=.5)
axs[2].set_ylabel('Force [N]')
axs[2].xaxis.set_major_locator(plt.MaxNLocator(4))
axs[2].yaxis.set_major_locator(plt.MaxNLocator(4))
axs[2].set_title('Tendon')
plt.suptitle('Muscle-tendon mechanics')
plt.tight_layout(w_pad=.1)
plt.show()
return axs
def lm_plot(self, x, axs=None):
"""Plot results of actdyn_ode45 function.
data = [t, lmt, lm, lt, vm, fm*fm0, fse*fm0, fl*fm0, fpe*fm0, alpha]
"""
try:
import matplotlib.pyplot as plt
except ImportError:
print('matplotlib is not available.')
return
if axs is None:
fig, axs = plt.subplots(nrows=3, ncols=2, sharex=True, figsize=(9, 6))
axs[0, 0].plot(x[:, 0], x[:, 1], 'b', label='LMT')
lmt = x[:, 2]*np.cos(x[:, 9]) + x[:, 3]
if np.sum(x[:, 9]) > 0:
axs[0, 0].plot(x[:, 0], lmt, 'g--', label=r'$LM \cos \alpha + LT$')
else:
axs[0, 0].plot(x[:, 0], lmt, 'g--', label=r'LM+LT')
ylim = self.margins(x[:, 1], margin=.1)
axs[0, 0].set_ylim(ylim)
axs[0, 0].legend(framealpha=.5, loc='best')
axs[0, 1].plot(x[:, 0], x[:, 3], 'b')
#axs[0, 1].plot(x[:, 0], lt0*np.ones(len(x)), 'r')
ylim = self.margins(x[:, 3], margin=.1)
axs[0, 1].set_ylim(ylim)
axs[1, 0].plot(x[:, 0], x[:, 2], 'b')
#axs[1, 0].plot(x[:, 0], lmopt*np.ones(len(x)), 'r')
ylim = self.margins(x[:, 2], margin=.1)
axs[1, 0].set_ylim(ylim)
axs[1, 1].plot(x[:, 0], x[:, 4], 'b')
ylim = self.margins(x[:, 4], margin=.1)
axs[1, 1].set_ylim(ylim)
axs[2, 0].plot(x[:, 0], x[:, 5], 'b', label='Muscle')
axs[2, 0].plot(x[:, 0], x[:, 6], 'g--', label='Tendon')
ylim = self.margins(x[:, [5, 6]], margin=.1)
axs[2, 0].set_ylim(ylim)
axs[2, 0].set_xlabel('Time (s)')
axs[2, 0].legend(framealpha=.5, loc='best')
axs[2, 1].plot(x[:, 0], x[:, 8], 'b', label='PE')
ylim = self.margins(x[:, 8], margin=.1)
axs[2, 1].set_ylim(ylim)
axs[2, 1].set_xlabel('Time (s)')
axs[2, 1].legend(framealpha=.5, loc='best')
ylabel = [r'$L_{MT}\,(m)$', r'$L_{T}\,(m)$', r'$L_{M}\,(m)$',
r'$V_{CE}\,(m/s)$', r'$Force\,(N)$', r'$Force\,(N)$']
for i, axi in enumerate(axs.flat):
axi.set_ylabel(ylabel[i])
axi.yaxis.set_major_locator(plt.MaxNLocator(4))
fig.align_ylabels(axs)
#axi.yaxis.set_label_coords(-.2, 0.5)
plt.suptitle('Simulation of muscle-tendon mechanics')
plt.tight_layout()
plt.show()
return axs
def penn_ang(self, lmt, lm, lt=None, lm0=None, alpha0=None):
"""Pennation angle.
Parameters
----------
lmt : float
muscle-tendon length
lt : float, optional (default=None)
tendon length
lm : float, optional (default=None)
muscle fiber length
lm0 : float, optional (default from states file)
initial muscle fiber length
alpha0 : float, optional (default from parameter file)
initial pennation angle
Returns
-------
alpha : float
pennation angle
"""
if lm0 is None: lm0 = self.S['lm0']
if alpha0 is None: alpha0 = self.P['alpha0']
alpha = alpha0
if alpha0 != 0:
w = lm0*np.sin(alpha0)
if lm is not None:
cosalpha = np.sqrt(1-(w/lm)**2)
elif lmt is not None and lt is not None:
cosalpha = 1/(np.sqrt(1 + (w/(lmt-lt))**2))
alpha = np.arccos(cosalpha)
if alpha > 1.4706289: # np.arccos(0.1), 84.2608 degrees
alpha = 1.4706289
return alpha
def excitation(self, t, u_max=None, u_min=None, t0=0, t1=5):
"""Excitation signal, a square wave.
Parameters
----------
t : float
time instant [s]
u_max : float (0 < u_max <= 1), optional (default from parameter file)
maximum value for muscle excitation
u_min : float (0 < u_min < 1), optional (default from parameter file)
minimum value for muscle excitation
t0 : float, optional (default=0)
initial time instant for muscle excitation equals to u_max [s]
t1 : float, optional (default=5)
final time instant for muscle excitation equals to u_max [s]
Returns
-------
u : float (0 < u <= 1)
excitation signal
"""
if u_max is None: u_max = self.P['u_max']
if u_min is None: u_min = self.P['u_min']
u = u_min
if t >= t0 and t <= t1:
u = u_max
return u
def activation_dyn(self, t, a, t_act=None, t_deact=None):
"""Thelen (2003) activation dynamics, the derivative of `a` at `t`.
Parameters
----------
t : float
time instant [s]
a : float (0 <= a <= 1)
muscle activation
t_act : float, optional (default from parameter file)
activation time constant [s]
t_deact : float, optional (default from parameter file)
deactivation time constant [s]
Returns
-------
adot : float
derivative of `a` at `t`
"""
if t_act is None: t_act = self.P['t_act']
if t_deact is None: t_deact = self.P['t_deact']
u = self.excitation(t)
if u > a:
adot = (u - a)/(t_act*(0.5 + 1.5*a))
else:
adot = (u - a)/(t_deact/(0.5 + 1.5*a))
return adot
def activation_sol(self, fun=None, t0=0, t1=3, a0=0, u_min=None,
t_act=None, t_deact=None, show=True, axs=None):
"""Runge-Kutta (4)5 ODE solver for activation dynamics.
Parameters
----------
fun : function object, optional (default is None and `actdyn` is used)
function with ODE to be solved
t0 : float, optional (default=0)
initial time instant for the simulation [s]
t1 : float, optional (default=0)
final time instant for the simulation [s]
a0 : float, optional (default=0)
initial muscle activation
u_max : float (0 < u_max <= 1), optional (default from parameter file)
maximum value for muscle excitation
u_min : float (0 < u_min < 1), optional (default from parameter file)
minimum value for muscle excitation
t_act : float, optional (default from parameter file)
activation time constant [s]
t_deact : float, optional (default from parameter file)
deactivation time constant [s]
show : bool, optional (default = True)
if True (1), plot data in matplotlib figure
axs : a matplotlib.axes.Axes instance, optional (default = None)
Returns
-------
data : 2-d array
array with columns [time, excitation, activation]
"""
if u_min is None: u_min = self.P['u_min']
if t_act is None: t_act = self.P['t_act']
if t_deact is None: t_deact = self.P['t_deact']
if fun is None:
fun = self.activation_dyn
f = ode(fun).set_integrator('dopri5', nsteps=1, max_step=0.005, atol=1e-8)
f.set_initial_value(a0, t0).set_f_params(t_act, t_deact)
# suppress Fortran warning
warnings.filterwarnings("ignore", category=UserWarning)
data = []
while f.t < t1:
f.integrate(t1, step=True)
data.append([f.t, self.excitation(f.t), np.max([f.y[0], u_min])])
warnings.resetwarnings()
data = np.array(data)
if show:
self.actvation_plot(data, axs)
self.act_data = data
return data
def activation(self, t=None):
"""Activation signal."""
data = self.act_data
if t is not None and len(data):
if t <= self.act_data[0, 0]:
a = self.act_data[0, 2]
elif t >= self.act_data[-1, 0]:
a = self.act_data[-1, 2]
else:
a = np.interp(t, self.act_data[:, 0], self.act_data[:, 2])
else:
a = 1
return a
def actvation_plot(self, data, axs=None):
"""Plot results of actdyn_ode45 function."""
try:
import matplotlib.pyplot as plt
except ImportError:
print('matplotlib is not available.')
return
if axs is None:
_, axs = plt.subplots(nrows=1, ncols=1, figsize=(6, 4))
axs.plot(data[:, 0], data[:, 1], color=[1, 0, 0, .6], label='Excitation')
axs.plot(data[:, 0], data[:, 2], color=[0, 0, 1, .6], label='Activation')
axs.set_xlabel('Time [s]')
axs.set_ylabel('Level')
axs.legend()
plt.title('Activation dynamics')
plt.tight_layout()
plt.show()
return axs
def margins(self, x, margin=0.01, minmargin=True):
"""Calculate plot limits with extra margins.
"""
rang = np.nanmax(x) - np.nanmin(x)
if rang < 0.001 and minmargin:
rang = 0.001*np.nanmean(x)/margin
if rang < 1:
rang = 1
lim = [np.nanmin(x) - rang*margin, np.nanmax(x) + rang*margin]
return lim