集体智慧编程¶
集体智慧是指为了创造新想法,将一群人的行为、偏好或思想组合在一起。一般基于聪明的算法(Netflix, Google)或者提供内容的用户(Wikipedia)。
集体智慧编程所强调的是前者,即通过编写计算机程序、构造具有智能的算法收集并分析用户的数据,发现新的信息甚至是知识。
- Netflix
- Wikipedia
Toby Segaran, 2007, Programming Collective Intelligence. O'Reilly.
推荐系统¶
- 目前互联网世界最常见的智能产品形式。
- 从信息时代过渡到注意力时代:
- 信息过载(information overload)
- 注意力稀缺
- 推荐系统的基本任务是联系用户和物品,帮助用户快速发现有用信息,解决信息过载的问题。
- 针对长尾分布问题,找到个性化需求,优化资源配置
推荐系统的类型¶
- 社会化推荐(Social Recommendation)
- 让朋友帮助推荐物品
- 基于内容的推荐 (Content-based filtering)
- 基于用户已经消费的物品内容,推荐新的物品。例如根据看过的电影的导演和演员,推荐新影片。
- 基于协同过滤的推荐(collaborative filtering)
- 找到和某用户的历史兴趣一致的用户,根据这些用户之间的相似性或者他们所消费物品的相似性,为该用户推荐物品
协同过滤算法¶
- 基于邻域的方法(neighborhood-based method)
- 基于用户的协同过滤(user-based filtering)
- 基于物品的协同过滤 (item-based filtering)
- 隐语义模型(latent factor model)
- 基于图的随机游走算法(random walk on graphs)
UserCF和ItemCF的比较¶
- UserCF较为古老, 1992年应用于电子邮件个性化推荐系统Tapestry, 1994年应用于Grouplens新闻个性化推荐, 后来被Digg采用
- 推荐那些与个体有共同兴趣爱好的用户所喜欢的物品(群体热点,社会化)
- 反映用户所在小型群体中物品的热门程度
- 推荐那些与个体有共同兴趣爱好的用户所喜欢的物品(群体热点,社会化)
- ItemCF相对较新,应用于电子商务网站Amazon和DVD租赁网站Netflix
- 推荐那些和用户之前喜欢的物品相似的物品 (历史兴趣,个性化)
- 反映了用户自己的兴趣传承
- 推荐那些和用户之前喜欢的物品相似的物品 (历史兴趣,个性化)
- 新闻更新快,物品数量庞大,相似度变化很快,不利于维护一张物品相似度的表格,电影、音乐、图书则可以。
推荐系统评测¶
- 用户满意度
预测准确度
$r_{ui}$用户实际打分, $\hat{r_{ui}}$推荐算法预测打分, T为测量次数
均方根误差RMSE
$RMSE = \sqrt{\frac{\sum_{u, i \in T} (r_{ui} - \hat{r_{ui}})}{ T }^2} $
平均绝对误差MAE
$ MAE = \frac{\sum_{u, i \in T} \left | r_{ui} - \hat{r_{ui}} \right|}{ T}$
# A dictionary of movie critics and their ratings of a small
# set of movies
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,
'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,
'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 3.5},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0,
'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0,
'The Night Listener': 4.5, 'Superman Returns': 4.0,
'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0,
'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5,'You, Me and Dupree':1.0,'Superman Returns':4.0}}
critics['Lisa Rose']['Lady in the Water']
2.5
critics['Toby']['Snakes on a Plane']
4.5
critics['Toby']
{'Snakes on a Plane': 4.5, 'Superman Returns': 4.0, 'You, Me and Dupree': 1.0}
# 欧几里得距离
import numpy as np
np.sqrt(np.power(5-4, 2) + np.power(4-1, 2))
3.1622776601683795
- This formula calculates the distance, which will be smaller for people who are more similar.
- However, you need a function that gives higher values for people who are similar.
- This can be done by adding 1 to the function (so you don’t get a division-by-zero error) and inverting it:
1.0 /(1 + np.sqrt(np.power(5-4, 2) + np.power(4-1, 2)) )
0.2402530733520421
# Returns a distance-based similarity score for person1 and person2
def sim_distance(prefs,person1,person2):
# Get the list of shared_items
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
# if they have no ratings in common, return 0
if len(si)==0: return 0
# Add up the squares of all the differences
sum_of_squares=np.sum([np.power(prefs[person1][item]-prefs[person2][item],2)
for item in prefs[person1] if item in prefs[person2]])
#for item in si.keys()])#
return 1/(1+np.sqrt(sum_of_squares) )
sim_distance(critics, 'Lisa Rose','Toby')
0.3483314773547883
Pearson correlation coefficient¶
# Returns the Pearson correlation coefficient for p1 and p2
def sim_pearson(prefs,p1,p2):
# Get the list of mutually rated items
si={}
for item in prefs[p1]:
if item in prefs[p2]: si[item]=1
# Find the number of elements
n=len(si)
# if they are no ratings in common, return 0
if n==0: return 0
# Add up all the preferences
sum1=np.sum([prefs[p1][it] for it in si])
sum2=np.sum([prefs[p2][it] for it in si])
# Sum up the squares
sum1Sq=np.sum([np.power(prefs[p1][it],2) for it in si])
sum2Sq=np.sum([np.power(prefs[p2][it],2) for it in si])
# Sum up the products
pSum=np.sum([prefs[p1][it]*prefs[p2][it] for it in si])
# Calculate Pearson score
num=pSum-(sum1*sum2/n)
den=np.sqrt((sum1Sq-np.power(sum1,2)/n)*(sum2Sq-np.power(sum2,2)/n))
if den==0: return 0
return num/den
sim_pearson(critics, 'Lisa Rose','Toby')
0.9912407071619299
# Returns the best matches for person from the prefs dictionary.
# Number of results and similarity function are optional params.
def topMatches(prefs,person,n=5,similarity=sim_pearson):
scores=[(similarity(prefs,person,other),other)
for other in prefs if other!=person]
# Sort the list so the highest scores appear at the top
scores.sort( )
scores.reverse( )
return scores[0:n]
topMatches(critics,'Toby',n=3) # topN
[(0.9912407071619299, 'Lisa Rose'), (0.9244734516419049, 'Mick LaSalle'), (0.8934051474415647, 'Claudia Puig')]
1.1 Recommending Items¶
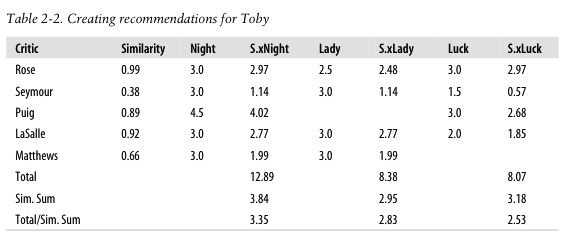
- Toby相似的五个用户(Rose, Reymour, Puig, LaSalle, Matthews)及相似度(依次为0.99, 0.38, 0.89, 0.92, 0.66)
- 这五个用户看过的三个电影(Night,Lady, Luck)及其评分
- 例如,Rose对Night评分是3.0
- S.xNight是用户相似度与电影评分的乘积
- 例如,Toby与Rose相似度(0.99) * Rose对Night评分是3.0 = 2.97
- 可以得到每部电影的得分
- 例如,Night的得分是12.89 = 2.97+1.14+4.02+2.77+1.99
- 电影得分需要使用用户相似度之和进行加权
- 例如,Night电影的预测得分是3.35 = 12.89/3.84
# Gets recommendations for a person by using a weighted average
# of every other user's rankings
def getRecommendations(prefs,person,similarity=sim_pearson):
totals={}
simSums={}
for other in prefs:
# don't compare me to myself
if other==person: continue
sim=similarity(prefs,person,other)
# ignore scores of zero or lower
if sim<=0: continue
for item in prefs[other]:
# only score movies I haven't seen yet
if item not in prefs[person]:# or prefs[person][item]==0:
# Similarity * Score
totals.setdefault(item,0)
totals[item]+=prefs[other][item]*sim
# Sum of similarities
simSums.setdefault(item,0)
simSums[item]+=sim
# Create the normalized list
rankings=[(total/simSums[item],item) for item,total in totals.items()]
# Return the sorted list
rankings.sort()
rankings.reverse()
return rankings
# Now you can find out what movies I should watch next:
getRecommendations(critics,'Toby')
[(3.3477895267131013, 'The Night Listener'), (2.8325499182641614, 'Lady in the Water'), (2.5309807037655645, 'Just My Luck')]
# You’ll find that the results are only affected very slightly by the choice of similarity metric.
getRecommendations(critics,'Toby',similarity=sim_distance)
[(3.457128694491423, 'The Night Listener'), (2.778584003814924, 'Lady in the Water'), (2.4224820423619167, 'Just My Luck')]
将item-user字典的键值翻转¶
# you just need to swap the people and the items.
def transformPrefs(prefs):
result={}
for person in prefs:
for item in prefs[person]:
result.setdefault(item,{})
# Flip item and person
result[item][person]=prefs[person][item]
return result
movies = transformPrefs(critics)
计算item的相似性¶
topMatches(movies,'Superman Returns')
[(0.65795169495976946, 'You, Me and Dupree'), (0.48795003647426888, 'Lady in the Water'), (0.11180339887498941, 'Snakes on a Plane'), (-0.17984719479905439, 'The Night Listener'), (-0.42289003161103106, 'Just My Luck')]
给item推荐user¶
def calculateSimilarItems(prefs,n=10):
# Create a dictionary of items showing which other items they
# are most similar to.
result={}
# Invert the preference matrix to be item-centric
itemPrefs=transformPrefs(prefs)
c=0
for item in itemPrefs:
# Status updates for large datasets
c+=1
if c%100==0:
print("%d / %d" % (c,len(itemPrefs)))
# Find the most similar items to this one
scores=topMatches(itemPrefs,item,n=n,similarity=sim_distance)
result[item]=scores
return result
itemsim=calculateSimilarItems(critics)
itemsim['Superman Returns']
[(0.3090169943749474, 'Snakes on a Plane'), (0.252650308587072, 'The Night Listener'), (0.2402530733520421, 'Lady in the Water'), (0.20799159651347807, 'Just My Luck'), (0.1918253663634734, 'You, Me and Dupree')]

- Toby看过三个电影(snakes、Superman、dupree)和评分(依次是4.5、4.0、1.0)
- 表格2-3给出这三部电影与另外三部电影的相似度
- 例如superman与night的相似度是0.103
- R.xNight表示Toby对自己看过的三部定影的评分与Night这部电影相似度的乘积
- 例如,0.818 = 4.5*0.182
- 那么Toby对于Night的评分可以表达为0.818+0.412+0.148 = 1.378
- 已经知道Night相似度之和是0.182+0.103+0.148 = 0.433
- 那么Toby对Night的最终评分可以表达为:1.378/0.433 = 3.183
- 已经知道Night相似度之和是0.182+0.103+0.148 = 0.433
def getRecommendedItems(prefs,itemMatch,user):
userRatings=prefs[user]
scores={}
totalSim={}
# Loop over items rated by this user
for (item,rating) in userRatings.items( ):
# Loop over items similar to this one
for (similarity,item2) in itemMatch[item]:
# Ignore if this user has already rated this item
if item2 in userRatings: continue
# Weighted sum of rating times similarity
scores.setdefault(item2,0)
scores[item2]+=similarity*rating
# Sum of all the similarities
totalSim.setdefault(item2,0)
totalSim[item2]+=similarity
# Divide each total score by total weighting to get an average
rankings=[(score/totalSim[item],item) for item,score in scores.items( )]
# Return the rankings from highest to lowest
rankings.sort( )
rankings.reverse( )
return rankings
getRecommendedItems(critics,itemsim,'Toby')
[(3.1667425234070894, 'The Night Listener'), (2.9366294028444355, 'Just My Luck'), (2.8687673926264674, 'Lady in the Water')]
getRecommendations(movies,'Just My Luck')
[(4.0, 'Michael Phillips'), (3.0, 'Jack Matthews')]
getRecommendations(movies, 'You, Me and Dupree')
[(3.1637361366111816, 'Michael Phillips')]

基于物品的协同过滤算法的网络表示方法¶
# https://github.com/ParticleWave/RecommendationSystemStudy/blob/d1960056b96cfaad62afbfe39225ff680240d37e/PersonalRank.py
import os
import random
class Graph:
def __init__(self):
self.G = dict()
def addEdge(self, p, q):
if p not in self.G: self.G[p] = dict()
if q not in self.G: self.G[q] = dict()
self.G[p][q] = 1
self.G[q][p] = 1
def getGraphMatrix(self):
return self.G
graph = Graph()
graph.addEdge('A', 'a')
graph.addEdge('A', 'c')
graph.addEdge('B', 'a')
graph.addEdge('B', 'b')
graph.addEdge('B', 'c')
graph.addEdge('B', 'd')
graph.addEdge('C', 'c')
graph.addEdge('C', 'd')
G = graph.getGraphMatrix()
print(G.keys())
dict_keys(['A', 'a', 'C', 'd', 'B', 'c', 'b'])
G
{'A': {'a': 1, 'c': 1},
'B': {'a': 1, 'b': 1, 'c': 1, 'd': 1},
'C': {'c': 1, 'd': 1},
'a': {'A': 1, 'B': 1},
'b': {'B': 1},
'c': {'A': 1, 'B': 1, 'C': 1},
'd': {'B': 1, 'C': 1}}
def PersonalRank(G, alpha, root, max_step):
# G is the biparitite graph of users' ratings on items
# alpha is the probability of random walk forward
# root is the studied User
# max_step if the steps of iterations.
rank = dict()
rank = {x:0.0 for x in G.keys()}
rank[root] = 1.0
for k in range(max_step):
tmp = {x:0.0 for x in G.keys()}
for i,ri in G.items():
for j,wij in ri.items():
if j not in tmp: tmp[j] = 0.0 #
tmp[j] += alpha * rank[i] / (len(ri)*1.0)
if j == root: tmp[j] += 1.0 - alpha
rank = tmp
print(k, rank)
return rank
PersonalRank(G, 0.8, 'A', 20)
# print(PersonalRank(G, 0.8, 'B', 20))
# print(PersonalRank(G, 0.8, 'C', 20))
0 {'A': 0.3999999999999999, 'd': 0.0, 'C': 0.0, 'a': 0.4, 'B': 0.0, 'c': 0.4, 'b': 0.0}
1 {'A': 0.6666666666666666, 'd': 0.0, 'C': 0.10666666666666669, 'a': 0.15999999999999998, 'B': 0.2666666666666667, 'c': 0.15999999999999998, 'b': 0.0}
2 {'A': 0.5066666666666666, 'd': 0.09600000000000003, 'C': 0.04266666666666666, 'a': 0.32, 'B': 0.10666666666666665, 'c': 0.3626666666666667, 'b': 0.053333333333333344}
3 {'A': 0.624711111111111, 'd': 0.03839999999999999, 'C': 0.13511111111111113, 'a': 0.22399999999999998, 'B': 0.3057777777777778, 'c': 0.24106666666666665, 'b': 0.02133333333333333}
4 {'A': 0.5538844444444444, 'd': 0.11520000000000002, 'C': 0.07964444444444443, 'a': 0.31104, 'B': 0.1863111111111111, 'c': 0.36508444444444443, 'b': 0.06115555555555557}
5 {'A': 0.6217718518518518, 'd': 0.06911999999999999, 'C': 0.14343585185185187, 'a': 0.258816, 'B': 0.31677629629629633, 'c': 0.29067377777777775, 'b': 0.03726222222222222}
6 {'A': 0.5810394074074073, 'd': 0.12072960000000002, 'C': 0.1051610074074074, 'a': 0.312064, 'B': 0.23849718518518517, 'c': 0.3694383407407408, 'b': 0.06335525925925926}
7 {'A': 0.6233424908641975, 'd': 0.08976384, 'C': 0.14680873086419757, 'a': 0.2801152, 'B': 0.322318538271605, 'c': 0.322179602962963, 'b': 0.04769943703703704}
8 {'A': 0.5979606407901235, 'd': 0.12318720000000004, 'C': 0.12182009679012348, 'a': 0.313800704, 'B': 0.27202572641975314, 'c': 0.37252419634567907, 'b': 0.06446370765432101}
9 {'A': 0.624860067292181, 'd': 0.10313318400000002, 'C': 0.14861466569218112, 'a': 0.2935894016, 'B': 0.3257059134156379, 'c': 0.34231744031604944, 'b': 0.05440514528395063}
10 {'A': 0.6087204113909463, 'd': 0.12458704896000004, 'C': 0.13253792435094652, 'a': 0.3150852096, 'B': 0.29349780121810704, 'c': 0.37453107587687245, 'b': 0.06514118268312759}
11 {'A': 0.6259090374071659, 'd': 0.11171472998400003, 'C': 0.14970977315116601, 'a': 0.3021877248, 'B': 0.3278568031376681, 'c': 0.35520289454037857, 'b': 0.05869956024362141}
12 {'A': 0.6155958617974342, 'd': 0.12545526988800004, 'C': 0.1394066638710343, 'a': 0.31593497559039996, 'B': 0.3072414019859314, 'c': 0.3758188848508664, 'b': 0.06557136062753362}
13 {'A': 0.6265923595297243, 'd': 0.1172109459456, 'C': 0.1504004772487644, 'a': 0.30768662511615996, 'B': 0.3292315559869513, 'c': 0.3634492906645737, 'b': 0.061448280397186285}
14 {'A': 0.6199944608903503, 'd': 0.126006502096896, 'C': 0.14380418922212634, 'a': 0.31648325500928, 'B': 0.3160374635863394, 'c': 0.37664344590878573, 'b': 0.06584631119739026}
15 {'A': 0.6270315542460547, 'd': 0.12072916840611841, 'C': 0.1508408530811013, 'a': 0.311205277073408, 'B': 0.3301112040427255, 'c': 0.36872695276225853, 'b': 0.06320749271726787}
16 {'A': 0.6228092982326321, 'd': 0.12635858204098563, 'C': 0.14661885476571632, 'a': 0.316834862506967, 'B': 0.3216669597688938, 'c': 0.3771712037394075, 'b': 0.0660222408085451}
17 {'A': 0.6273129326666287, 'd': 0.1229809338600653, 'C': 0.15112242048023627, 'a': 0.3134571112468316, 'B': 0.3306741581298591, 'c': 0.37210465315311814, 'b': 0.06433339195377877}
18 {'A': 0.6246107520062307, 'd': 0.12658379981806633, 'C': 0.1484202810515243, 'a': 0.3170600046926233, 'B': 0.32526983911327995, 'c': 0.3775089728847178, 'b': 0.06613483162597182}
19 {'A': 0.627493061312974, 'd': 0.1244220802432657, 'C': 0.15130257936315128, 'a': 0.3148982686251483, 'B': 0.3310344465409781, 'c': 0.37426638104575805, 'b': 0.06505396782265599}
{'A': 0.627493061312974,
'B': 0.3310344465409781,
'C': 0.15130257936315128,
'a': 0.3148982686251483,
'b': 0.06505396782265599,
'c': 0.37426638104575805,
'd': 0.1244220802432657}
3. MovieLens Recommender¶
MovieLens是一个电影评价的真实数据,由明尼苏达州立大学的GroupLens项目组开发。
数据下载¶
http://grouplens.org/datasets/movielens/1m/
These files contain 1,000,209 anonymous ratings of approximately 3,900 movies made by 6,040 MovieLens users who joined MovieLens in 2000.
数据格式¶
All ratings are contained in the file "ratings.dat" and are in the following format:
UserID::MovieID::Rating::Timestamp
1::1193::5::978300760
1::661::3::978302109
1::914::3::978301968
def loadMovieLens(path='/Users/datalab/bigdata/cjc/ml-1m/'):
# Get movie titles
movies={}
for line in open(path+'movies.dat', encoding = 'iso-8859-15'):
(id,title)=line.split('::')[0:2]
movies[id]=title
# Load data
prefs={}
for line in open(path+'/ratings.dat'):
(user,movieid,rating,ts)=line.split('::')
prefs.setdefault(user,{})
prefs[user][movies[movieid]]=float(rating)
return prefs
prefs=loadMovieLens()
prefs['87']
{'Alice in Wonderland (1951)': 1.0,
'Army of Darkness (1993)': 3.0,
'Bad Boys (1995)': 5.0,
'Benji (1974)': 1.0,
'Brady Bunch Movie, The (1995)': 1.0,
'Braveheart (1995)': 5.0,
'Buffalo 66 (1998)': 1.0,
'Chambermaid on the Titanic, The (1998)': 1.0,
'Cowboy Way, The (1994)': 1.0,
'Cyrano de Bergerac (1990)': 4.0,
'Dear Diary (Caro Diario) (1994)': 1.0,
'Die Hard (1988)': 3.0,
'Diebinnen (1995)': 1.0,
'Dr. No (1962)': 1.0,
'Escape from the Planet of the Apes (1971)': 1.0,
'Fast, Cheap & Out of Control (1997)': 1.0,
'Faster Pussycat! Kill! Kill! (1965)': 1.0,
'From Russia with Love (1963)': 1.0,
'Fugitive, The (1993)': 5.0,
'Get Shorty (1995)': 1.0,
'Gladiator (2000)': 5.0,
'Goldfinger (1964)': 5.0,
'Good, The Bad and The Ugly, The (1966)': 4.0,
'Hunt for Red October, The (1990)': 5.0,
'Hurricane, The (1999)': 5.0,
'Indiana Jones and the Last Crusade (1989)': 4.0,
'Jaws (1975)': 5.0,
'Jurassic Park (1993)': 5.0,
'King Kong (1933)': 1.0,
'King of New York (1990)': 1.0,
'Last of the Mohicans, The (1992)': 1.0,
'Lethal Weapon (1987)': 5.0,
'Longest Day, The (1962)': 1.0,
'Man with the Golden Gun, The (1974)': 5.0,
'Mask of Zorro, The (1998)': 5.0,
'Matrix, The (1999)': 5.0,
"On Her Majesty's Secret Service (1969)": 1.0,
'Out of Sight (1998)': 1.0,
'Palookaville (1996)': 1.0,
'Planet of the Apes (1968)': 1.0,
'Pope of Greenwich Village, The (1984)': 1.0,
'Princess Bride, The (1987)': 3.0,
'Raiders of the Lost Ark (1981)': 4.0,
'Rock, The (1996)': 5.0,
'Rocky (1976)': 5.0,
'Saving Private Ryan (1998)': 4.0,
'Shanghai Noon (2000)': 1.0,
'Speed (1994)': 1.0,
'Star Wars: Episode IV - A New Hope (1977)': 5.0,
'Star Wars: Episode V - The Empire Strikes Back (1980)': 5.0,
'Taking of Pelham One Two Three, The (1974)': 1.0,
'Terminator 2: Judgment Day (1991)': 5.0,
'Terminator, The (1984)': 4.0,
'Thelma & Louise (1991)': 1.0,
'True Romance (1993)': 1.0,
'U-571 (2000)': 5.0,
'Untouchables, The (1987)': 5.0,
'Westworld (1973)': 1.0,
'X-Men (2000)': 4.0}
user-based filtering¶
getRecommendations(prefs,'87')[0:30]
[(5.0, 'Time of the Gypsies (Dom za vesanje) (1989)'), (5.0, 'Tigrero: A Film That Was Never Made (1994)'), (5.0, 'Schlafes Bruder (Brother of Sleep) (1995)'), (5.0, 'Return with Honor (1998)'), (5.0, 'Lured (1947)'), (5.0, 'Identification of a Woman (Identificazione di una donna) (1982)'), (5.0, 'I Am Cuba (Soy Cuba/Ya Kuba) (1964)'), (5.0, 'Hour of the Pig, The (1993)'), (5.0, 'Gay Deceivers, The (1969)'), (5.0, 'Gate of Heavenly Peace, The (1995)'), (5.0, 'Foreign Student (1994)'), (5.0, 'Dingo (1992)'), (5.0, 'Dangerous Game (1993)'), (5.0, 'Callejón de los milagros, El (1995)'), (5.0, 'Bittersweet Motel (2000)'), (4.820460101722989, 'Apple, The (Sib) (1998)'), (4.738956184936386, 'Lamerica (1994)'), (4.681816541467396, 'Bells, The (1926)'), (4.664958072522234, 'Hurricane Streets (1998)'), (4.650741840804562, 'Sanjuro (1962)'), (4.649974172600346, 'On the Ropes (1999)'), (4.636825408739504, 'Shawshank Redemption, The (1994)'), (4.627888709544556, 'For All Mankind (1989)'), (4.582048349280509, 'Midaq Alley (Callejón de los milagros, El) (1995)'), (4.579778646871153, "Schindler's List (1993)"), (4.57519994103739, 'Seven Samurai (The Magnificent Seven) (Shichinin no samurai) (1954)'), (4.574904988403455, 'Godfather, The (1972)'), (4.5746840191882345, "Ed's Next Move (1996)"), (4.558519037147828, 'Hanging Garden, The (1997)'), (4.527760042775589, 'Close Shave, A (1995)')]
Item-based filtering¶
itemsim=calculateSimilarItems(prefs,n=50)
100 / 3706 200 / 3706 300 / 3706 400 / 3706 500 / 3706 600 / 3706 700 / 3706 800 / 3706 900 / 3706 1000 / 3706
getRecommendedItems(prefs,itemsim,'87')[0:30]
[(5.0, 'Uninvited Guest, An (2000)'), (5.0, 'Two Much (1996)'), (5.0, 'Two Family House (2000)'), (5.0, 'Trial by Jury (1994)'), (5.0, 'Tom & Viv (1994)'), (5.0, 'This Is My Father (1998)'), (5.0, 'Something to Sing About (1937)'), (5.0, 'Slappy and the Stinkers (1998)'), (5.0, 'Running Free (2000)'), (5.0, 'Roula (1995)'), (5.0, 'Prom Night IV: Deliver Us From Evil (1992)'), (5.0, 'Project Moon Base (1953)'), (5.0, 'Price Above Rubies, A (1998)'), (5.0, 'Open Season (1996)'), (5.0, 'Only Angels Have Wings (1939)'), (5.0, 'Onegin (1999)'), (5.0, 'Once Upon a Time... When We Were Colored (1995)'), (5.0, 'Office Killer (1997)'), (5.0, 'N\xe9nette et Boni (1996)'), (5.0, 'No Looking Back (1998)'), (5.0, 'Never Met Picasso (1996)'), (5.0, 'Music From Another Room (1998)'), (5.0, "Mummy's Tomb, The (1942)"), (5.0, 'Modern Affair, A (1995)'), (5.0, 'Machine, The (1994)'), (5.0, 'Lured (1947)'), (5.0, 'Low Life, The (1994)'), (5.0, 'Lodger, The (1926)'), (5.0, 'Loaded (1994)'), (5.0, 'Line King: Al Hirschfeld, The (1996)')]
Buiding Recommendation System with GraphLab¶
In this notebook we will import GraphLab Create and use it to
- train two models that can be used for recommending new songs to users
- compare the performance of the two models
# set product key using GraphLab Create API
#import graphlab
#graphlab.product_key.set_product_key('4972-65DF-8E02-816C-AB15-021C-EC1B-0367')
%matplotlib inline
import graphlab
# set canvas to show sframes and sgraphs in ipython notebook
graphlab.canvas.set_target('ipynb')
import matplotlib.pyplot as plt
sf = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"],
'rating': [1, 3, 2, 5, 4, 1, 4, 3]})
sf
| item_id | rating | user_id |
|---|---|---|
| a | 1 | 0 |
| b | 3 | 0 |
| c | 2 | 0 |
| a | 5 | 1 |
| b | 4 | 1 |
| b | 1 | 2 |
| c | 4 | 2 |
| d | 3 | 2 |
m = graphlab.recommender.create(sf, target='rating')
recs = m.recommend()
recs
Recsys training: model = ranking_factorization_recommender
Preparing data set.
Data has 8 observations with 3 users and 4 items.
Data prepared in: 0.007151s
Training ranking_factorization_recommender for recommendations.
+--------------------------------+--------------------------------------------------+----------+
| Parameter | Description | Value |
+--------------------------------+--------------------------------------------------+----------+
| num_factors | Factor Dimension | 32 |
| regularization | L2 Regularization on Factors | 1e-09 |
| solver | Solver used for training | sgd |
| linear_regularization | L2 Regularization on Linear Coefficients | 1e-09 |
| ranking_regularization | Rank-based Regularization Weight | 0.25 |
| max_iterations | Maximum Number of Iterations | 25 |
+--------------------------------+--------------------------------------------------+----------+
Optimizing model using SGD; tuning step size.
Using 8 / 8 points for tuning the step size.
+---------+-------------------+------------------------------------------+
| Attempt | Initial Step Size | Estimated Objective Value |
+---------+-------------------+------------------------------------------+
| 0 | 25 | Not Viable |
| 1 | 6.25 | Not Viable |
| 2 | 1.5625 | Not Viable |
| 3 | 0.390625 | 2.80914 |
| 4 | 0.195312 | 2.73981 |
| 5 | 0.0976562 | 2.81555 |
| 6 | 0.0488281 | 3.00079 |
| 7 | 0.0244141 | 3.28347 |
+---------+-------------------+------------------------------------------+
| Final | 0.195312 | 2.73981 |
+---------+-------------------+------------------------------------------+
Starting Optimization.
+---------+--------------+-------------------+-----------------------+-------------+
| Iter. | Elapsed Time | Approx. Objective | Approx. Training RMSE | Step Size |
| user_id | item_id | score | rank |
|---|---|---|---|
| 0 | d | 1.25723338127 | 1 |
| 1 | c | 4.00432437658 | 1 |
| 1 | d | 3.11584371328 | 2 |
| 2 | a | 2.48449929804 | 1 |
+---------+--------------+-------------------+-----------------------+-------------+
| Initial | 112us | 3.89999 | 1.3637 | |
+---------+--------------+-------------------+-----------------------+-------------+
| 1 | 801us | 4.11274 | 1.60028 | 0.195312 |
| 2 | 1.886ms | 3.00599 | 1.39719 | 0.116134 |
| 3 | 2.461ms | 2.66992 | 1.19539 | 0.0856819 |
| 4 | 3.164ms | 2.47924 | 1.14458 | 0.0580668 |
| 5 | 3.803ms | 2.42201 | 1.15439 | 0.0491185 |
| 6 | 4.46ms | 2.38401 | 1.16223 | 0.042841 |
| 11 | 7.446ms | 2.27653 | 1.09388 | 0.0271912 |
+---------+--------------+-------------------+-----------------------+-------------+
Optimization Complete: Maximum number of passes through the data reached.
Computing final objective value and training RMSE.
Final objective value: 2.79501
Final training RMSE: 1.04275
help(m)
Help on RankingFactorizationRecommender in module graphlab.toolkits.recommender.ranking_factorization_recommender object:
class RankingFactorizationRecommender(graphlab.toolkits.recommender.util._Recommender)
| A RankingFactorizationRecommender learns latent factors for each
| user and item and uses them to rank recommended items according to
| the likelihood of observing those (user, item) pairs. This is
| commonly desired when performing collaborative filtering for
| implicit feedback datasets or datasets with explicit ratings
| for which ranking prediction is desired.
|
| RankingFactorizationRecommender contains a number of options that
| tailor to a variety of datasets and evaluation metrics, making
| this one of the most powerful models in the GraphLab Create
| recommender toolkit.
|
| **Creating a RankingFactorizationRecommender**
|
| This model cannot be constructed directly. Instead, use
| :func:`graphlab.recommender.ranking_factorization_recommender.create`
| to create an instance
| of this model. A detailed list of parameter options and code samples
| are available in the documentation for the create function.
|
| **Side information**
|
| Side features may be provided via the `user_data` and `item_data` options
| when the model is created.
|
| Additionally, observation-specific information, such as the time of day when
| the user rated the item, can also be included. Any column in the
| `observation_data` SFrame that is not the user id, item id, or target is
| treated as a observation side features. The same side feature columns must
| be present when calling :meth:`predict`.
|
| Side features may be numeric or categorical. User ids and item ids are
| treated as categorical variables. For the additional side features, the type
| of the :class:`~graphlab.SFrame` column determines how it's handled: strings
| are treated as categorical variables and integers and floats are treated as
| numeric variables. Dictionaries and numeric arrays are also supported.
|
| **Optimizing for ranking performance**
|
| By default, RankingFactorizationRecommender optimizes for the
| precision-recall performance of recommendations.
|
| **Model parameters**
|
| Trained model parameters may be accessed using
| `m.get('coefficients')` or equivalently `m['coefficients']`, where `m`
| is a RankingFactorizationRecommender.
|
| See Also
| --------
| create, :func:`graphlab.recommender.factorization_recommender.create`
|
| Notes
| -----
|
| **Model Details**
|
| `RankingFactorizationRecommender` trains a model capable of predicting a score for
| each possible combination of users and items. The internal coefficients of
| the model are learned from known scores of users and items.
| Recommendations are then based on these scores.
|
| In the two factorization models, users and items are represented by weights
| and factors. These model coefficients are learned during training.
| Roughly speaking, the weights, or bias terms, account for a user or item's
| bias towards higher or lower ratings. For example, an item that is
| consistently rated highly would have a higher weight coefficient associated
| with them. Similarly, an item that consistently receives below average
| ratings would have a lower weight coefficient to account for this bias.
|
| The factor terms model interactions between users and items. For example,
| if a user tends to love romance movies and hate action movies, the factor
| terms attempt to capture that, causing the model to predict lower scores
| for action movies and higher scores for romance movies. Learning good
| weights and factors is controlled by several options outlined below.
|
| More formally, the predicted score for user :math:`i` on item :math:`j` is
| given by
|
| .. math::
| \operatorname{score}(i, j) =
| \mu + w_i + w_j
| + \mathbf{a}^T \mathbf{x}_i + \mathbf{b}^T \mathbf{y}_j
| + {\mathbf u}_i^T {\mathbf v}_j,
|
| where :math:`\mu` is a global bias term, :math:`w_i` is the weight term for
| user :math:`i`, :math:`w_j` is the weight term for item :math:`j`,
| :math:`\mathbf{x}_i` and :math:`\mathbf{y}_j` are respectively the user and
| item side feature vectors, and :math:`\mathbf{a}` and :math:`\mathbf{b}`
| are respectively the weight vectors for those side features.
| The latent factors, which are vectors of length ``num_factors``, are given
| by :math:`{\mathbf u}_i` and :math:`{\mathbf v}_j`.
|
|
| **Training the model**
|
| The model is trained using Stochastic Gradient Descent [sgd]_ with additional
| tricks [Bottou]_ to improve convergence. The optimization is done in parallel
| over multiple threads. This procedure is inherently random, so different
| calls to `create()` may return slightly different models, even with the
| same `random_seed`.
|
| In the explicit rating case, the objective function we are
| optimizing for is:
|
| .. math::
| \min_{\mathbf{w}, \mathbf{a}, \mathbf{b}, \mathbf{V}, \mathbf{U}}
| \frac{1}{|\mathcal{D}|} \sum_{(i,j,r_{ij}) \in \mathcal{D}}
| \mathcal{L}(\operatorname{score}(i, j), r_{ij})
| + \lambda_1 (\lVert {\mathbf w} \rVert^2_2 + || {\mathbf a} ||^2_2 + || {\mathbf b} ||^2_2 )
| + \lambda_2 \left(\lVert {\mathbf U} \rVert^2_2
| + \lVert {\mathbf V} \rVert^2_2 \right)
|
| where :math:`\mathcal{D}` is the observation dataset, :math:`r_{ij}` is the
| rating that user :math:`i` gave to item :math:`j`,
| :math:`{\mathbf U} = ({\mathbf u}_1, {\mathbf u}_2, ...)` denotes the user's
| latent factors and :math:`{\mathbf V} = ({\mathbf v}_1, {\mathbf v}_2, ...)`
| denotes the item latent factors. The loss function
| :math:`\mathcal{L}(\hat{y}, y)` is :math:`(\hat{y} - y)^2` by default.
| :math:`\lambda_1` denotes the `linear_regularization` parameter and
| :math:`\lambda_2` the `regularization` parameter.
|
| When ``ranking_regularization`` is nonzero, then the equation
| above gets an additional term. Let :math:`\lambda_{\text{rr}}` represent
| the value of `ranking_regularization`, and let
| :math:`v_{\text{ur}}` represent `unobserved_rating_value`. Then the
| objective we attempt to minimize is:
|
| .. math::
| \min_{\mathbf{w}, \mathbf{a}, \mathbf{b}, \mathbf{V}, \mathbf{U}}
| \frac{1}{|\mathcal{D}|} \sum_{(i,j,r_{ij}) \in \mathcal{D}}
| \mathcal{L}(\operatorname{score}(i, j), r_{ij})
| + \lambda_1 (\lVert {\mathbf w} \rVert^2_2 + || {\mathbf a} ||^2_2 + || {\mathbf b} ||^2_2 )
| + \lambda_2 \left(\lVert {\mathbf U} \rVert^2_2
| + \lVert {\mathbf V} \rVert^2_2 \right) \\
| + \frac{\lambda_{rr}}{\text{const} * |\mathcal{U}|}
| \sum_{(i,j) \in \mathcal{U}}
| \mathcal{L}\left(\operatorname{score}(i, j), v_{\text{ur}}\right),
|
| where :math:`\mathcal{U}` is a sample of unobserved user-item pairs.
|
| In the implicit case when there are no target values, we use
| logistic loss to fit a model that attempts to predict all the
| given (user, item) pairs in the training data as 1 and all others
| as 0. To train this model, we sample an unobserved item along
| with each observed (user, item) pair, using SGD to push the score
| of the observed pair towards 1 and the unobserved pair towards 0.
| In this case, the `ranking_regularization` parameter is ignored.
|
| When `binary_targets=True`, then the target values must be 0 or 1;
| in this case, we also use logistic loss to train the model so the
| predicted scores are as close to the target values as possible.
| This time, the rating of the sampled unobserved pair is set to 0
| (thus the `unobserved_rating_value` is ignored). In this case,
| the loss on the unobserved pairs is weighted by
| `ranking_regularization` as in the non-binary case.
|
| To choose the unobserved pair complementing a given observation,
| the algorithm selects several (defaults to four) candidate
| negative items that the user in the given observation has not
| rated. The algorithm scores each one using the current model, then
| chooses the item with the largest predicted score. This adaptive
| sampling strategy provides faster convergence than just sampling a
| single negative item.
|
| The Factorization Machine [Rendle]_ is a generalization of Matrix
| Factorization. Like matrix factorization, it predicts target
| rating values as a weighted combination of user and item latent
| factors, biases, side features, and their pairwise combinations.
| In particular, while Matrix Factorization learns latent factors
| for only the user and item interactions, the Factorization Machine
| learns latent factors for all variables, including side features,
| and also allows for interactions between all pairs of
| variables. Thus the Factorization Machine is capable of modeling
| complex relationships in the data. Typically, using
| `linear_side_features=True` performs better in terms of RMSE, but
| may require a longer training time.
|
| num_sampled_negative_examples: For each (user, item) pair in the data, the
| ranking sgd solver evaluates this many randomly chosen unseen items for the
| negative example step. Increasing this can give better performance at the
| expense of speed, particularly when the number of items is large.
|
|
| When `ranking_regularization` is larger than zero, the model samples
| a small set of unobserved user-item pairs and attempts to drive their rating
| predictions below the value specified with `unobserved_rating_value`.
| This has the effect of improving the precision-recall performance of
| recommended items.
|
|
| ** Implicit Matrix Factorization**
|
| `RankingFactorizationRecommender` had an additional option of optimizing
| for ranking using the implcit matrix factorization model. The internal coefficients of
| the model and its interpretation are identical to the model described above.
| The difference between the two models is in the nature in which the objective
| is achieved. Currently, this model does not incorporate any columns
| beyond user/item (and rating) or side data.
|
|
| The model works by transferring the raw observations (or weights) (r) into
| two separate magnitudes with distinct interpretations: preferences (p) and
| confidence levels (c). The functional relationship between the weights (r)
| and the confidence is either linear or logarithmic which can be toggled
| by setting `ials_confidence_scaling_type` = `linear` (the default) or `log`
| respectively. The rate of increase of the confidence with respect to the
| weights is proportional to the `ials_confidence_scaling_factor`
| (default 1.0).
|
|
| Examples
| --------
| **Basic usage**
|
| >>> sf = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
| ... 'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"],
| ... 'rating': [1, 3, 2, 5, 4, 1, 4, 3]})
| >>> m1 = graphlab.ranking_factorization_recommender.create(sf, target='rating')
|
| For implicit data, no target column is specified:
|
| >>> sf = graphlab.SFrame({'user': ["0", "0", "0", "1", "1", "2", "2", "2"],
| ... 'movie': ["a", "b", "c", "a", "b", "b", "c", "d"]})
| >>> m2 = graphlab.ranking_factorization_recommender.create(sf, 'user', 'movie')
|
| **Implicit Matrix Factorization**
|
| >>> sf = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
| ... 'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"],
| ... 'rating': [1, 3, 2, 5, 4, 1, 4, 3]})
| >>> m1 = graphlab.ranking_factorization_recommender.create(sf, target='rating',
| solver='ials')
|
| For implicit data, no target column is specified:
|
| >>> sf = graphlab.SFrame({'user': ["0", "0", "0", "1", "1", "2", "2", "2"],
| ... 'movie': ["a", "b", "c", "a", "b", "b", "c", "d"]})
| >>> m2 = graphlab.ranking_factorization_recommender.create(sf, 'user', 'movie',
| solver='ials')
|
| **Including side features**
|
| >>> user_info = graphlab.SFrame({'user_id': ["0", "1", "2"],
| ... 'name': ["Alice", "Bob", "Charlie"],
| ... 'numeric_feature': [0.1, 12, 22]})
| >>> item_info = graphlab.SFrame({'item_id': ["a", "b", "c", d"],
| ... 'name': ["item1", "item2", "item3", "item4"],
| ... 'dict_feature': [{'a' : 23}, {'a' : 13},
| ... {'b' : 1},
| ... {'a' : 23, 'b' : 32}]})
| >>> m2 = graphlab.ranking_factorization_recommender.create(sf,
| ... target='rating',
| ... user_data=user_info,
| ... item_data=item_info)
|
| **Optimizing for ranking performance**
|
| Create a model that pushes predicted ratings of unobserved user-item
| pairs toward 1 or below.
|
| >>> m3 = graphlab.ranking_factorization_recommender.create(sf,
| ... target='rating',
| ... ranking_regularization = 0.1,
| ... unobserved_rating_value = 1)
|
| Method resolution order:
| RankingFactorizationRecommender
| graphlab.toolkits.recommender.util._Recommender
| graphlab.toolkits._model.Model
| graphlab.toolkits._model.CustomModel
| graphlab.toolkits._model.ProxyBasedModel
| __builtin__.object
|
| Methods defined here:
|
| __init__(self, model_proxy)
| __init__(self)
|
| ----------------------------------------------------------------------
| Methods inherited from graphlab.toolkits.recommender.util._Recommender:
|
| __repr__(self)
| Returns a string description of the model, including (where relevant)
| the schema of the training data, description of the training data,
| training statistics, and model hyperparameters.
|
| Returns
| -------
| out : string
| A description of the model.
|
| __str__(self)
| Returns the type of model.
|
| Returns
| -------
| out : string
| The type of model.
|
| evaluate(model, *args, **kwargs)
| Evaluate the model's ability to make rating predictions or
| recommendations.
|
| If the model is trained to predict a particular target, the
| default metric used for model comparison is root-mean-squared error
| (RMSE). Suppose :math:`y` and :math:`\widehat{y}` are vectors of length
| :math:`N`, where :math:`y` contains the actual ratings and
| :math:`\widehat{y}` the predicted ratings. Then the RMSE is defined as
|
| .. math::
|
| RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^N (\widehat{y}_i - y_i)^2} .
|
| If the model was not trained on a target column, the default metrics for
| model comparison are precision and recall. Let
| :math:`p_k` be a vector of the :math:`k` highest ranked recommendations
| for a particular user, and let :math:`a` be the set of items for that
| user in the groundtruth `dataset`. The "precision at cutoff k" is
| defined as
|
| .. math:: P(k) = \frac{ | a \cap p_k | }{k}
|
| while "recall at cutoff k" is defined as
|
| .. math:: R(k) = \frac{ | a \cap p_k | }{|a|}
|
| Parameters
| ----------
| dataset : SFrame
| An SFrame that is in the same format as provided for training.
|
| metric : str, {'auto', 'rmse', 'precision_recall'}, optional
| Metric to use for evaluation. The default automatically chooses
| 'rmse' for models trained with a `target`, and 'precision_recall'
| otherwise.
|
| exclude_known_for_precision_recall : bool, optional
| A useful option for evaluating precision-recall. Recommender models
| have the option to exclude items seen in the training data from the
| final recommendation list. Set this option to True when evaluating
| on test data, and False when evaluating precision-recall on training
| data.
|
| target : str, optional
| The name of the target column for evaluating rmse. If the model is
| trained with a target column, the default is to using the same
| column. If the model is trained without a target column and `metric`
| is set to 'rmse', this option must provided by user.
|
| verbose : bool, optional
| Enables verbose output. Default is verbose.
|
| **kwargs
| When `metric` is set to 'precision_recall', these parameters
| are passed on to :meth:`evaluate_precision_recall`.
|
| Returns
| -------
| out : SFrame or dict
| Results from the model evaluation procedure. If the model is trained
| on a target (i.e. RMSE is the evaluation criterion), a dictionary
| with three items is returned: items *rmse_by_user* and
| *rmse_by_item* are SFrames with per-user and per-item RMSE, while
| *rmse_overall* is the overall RMSE (a float). If the model is
| trained without a target (i.e. precision and recall are the
| evaluation criteria) an :py:class:`~graphlab.SFrame` is returned
| with both of these metrics for each user at several cutoff values.
|
| Examples
| --------
| >>> import graphlab as gl
| >>> sf = gl.SFrame('https://static.turi.com/datasets/audioscrobbler')
| >>> train, test = gl.recommender.util.random_split_by_user(sf)
| >>> m = gl.recommender.create(train, target='target')
| >>> eval = m.evaluate(test)
|
| See Also
| --------
| evaluate_precision_recall, evaluate_rmse, precision_recall_by_user
|
| evaluate_precision_recall(self, dataset, cutoffs=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 16, 21, 26, 31, 36, 41, 46], skip_set=None, exclude_known=True, verbose=True, **kwargs)
| Compute a model's precision and recall scores for a particular dataset.
|
| Parameters
| ----------
| dataset : SFrame
| An SFrame in the same format as the one used during training.
| This will be compared to the model's recommendations, which exclude
| the (user, item) pairs seen at training time.
|
| cutoffs : list, optional
| A list of cutoff values for which one wants to evaluate precision
| and recall, i.e. the value of k in "precision at k".
|
| skip_set : SFrame, optional
| Passed to :meth:`recommend` as ``exclude``.
|
| exclude_known : bool, optional
| Passed to :meth:`recommend` as ``exclude_known``. If True, exclude
| training item from recommendation.
|
| verbose : bool, optional
| Enables verbose output. Default is verbose.
|
| **kwargs
| Additional keyword arguments are passed to the recommend
| function, whose returned recommendations are used for evaluating
| precision and recall of the model.
|
| Returns
| -------
| out : dict
| Contains the precision and recall at each cutoff value and each
| user in ``dataset``.
|
| Examples
| --------
|
| >>> import graphlab as gl
| >>> sf = gl.SFrame('https://static.turi.com/datasets/audioscrobbler')
| >>> train, test = gl.recommender.util.random_split_by_user(sf)
| >>> m = gl.recommender.create(train)
| >>> m.evaluate_precision_recall(test)
|
| See Also
| --------
| graphlab.recommender.util.precision_recall_by_user
|
| evaluate_rmse(self, dataset, target)
| Evaluate the prediction error for each user-item pair in the given data
| set.
|
| Parameters
| ----------
| dataset : SFrame
| An SFrame in the same format as the one used during training.
|
| target : str
| The name of the target rating column in `dataset`.
|
| Returns
| -------
| out : dict
| A dictionary with three items: 'rmse_by_user' and 'rmse_by_item',
| which are SFrames containing the average rmse for each user and
| item, respectively; and 'rmse_overall', which is a float.
|
| Examples
| --------
| >>> import graphlab as gl
| >>> sf = gl.SFrame('https://static.turi.com/datasets/audioscrobbler')
| >>> train, test = gl.recommender.util.random_split_by_user(sf)
| >>> m = gl.recommender.create(train, target='target')
| >>> m.evaluate_rmse(test, target='target')
|
| See Also
| --------
| graphlab.evaluation.rmse
|
| get(self, field)
| Get the value of a particular field.
|
| Parameters
| ----------
| field : string
| Name of the field to be retrieved.
|
| Returns
| -------
| out
| The current value of the requested field.
|
| Examples
| --------
| >>> data = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
| ... 'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"],
| ... 'rating': [1, 3, 2, 5, 4, 1, 4, 3]})
| >>> from graphlab.recommender
| >>> m = factorization_recommender.create(data, "user_id", "item_id", "rating")
| >>> d = m.get("coefficients")
| >>> U1 = d['user_id']
| >>> U2 = d['movie_id']
|
| get_current_options(self)
| A dictionary describing all the parameters of the given model
| and their current setting.
|
| get_num_items_per_user(self)
| Get the number of items observed for each user.
|
| Returns
| -------
| out : SFrame
| An SFrame with a column containing each observed user and another column
| containing the corresponding number of items observed during training.
|
| Examples
| --------
|
| get_num_users_per_item(self)
| Get the number of users observed for each item.
|
| Returns
| -------
| out : SFrame
| An SFrame with a column containing each observed item and another column
| containing the corresponding number of items observed during training.
|
| Examples
| --------
|
| get_similar_items(self, items=None, k=10, verbose=False)
| Get the k most similar items for each item in items.
|
| Each type of recommender has its own model for the similarity
| between items. For example, the item_similarity_recommender will
| return the most similar items according to the user-chosen
| similarity; the factorization_recommender will return the
| nearest items based on the cosine similarity between latent item
| factors.
|
| Parameters
| ----------
| items : SArray or list; optional
| An :class:`~graphlab.SArray` or list of item ids for which to get
| similar items. If 'None', then return the `k` most similar items for
| all items in the training set.
|
| k : int, optional
| The number of similar items for each item.
|
| verbose : bool, optional
| Progress printing is shown.
|
| Returns
| -------
| out : SFrame
| A SFrame with the top ranked similar items for each item. The
| columns `item`, 'similar', 'score' and 'rank', where
| `item` matches the item column name specified at training time.
| The 'rank' is between 1 and `k` and 'score' gives the similarity
| score of that item. The value of the score depends on the method
| used for computing item similarities.
|
| Examples
| --------
|
| >>> sf = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
| 'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"]})
| >>> m = graphlab.item_similarity_recommender.create(sf)
| >>> nn = m.get_similar_items()
|
| get_similar_users(self, users=None, k=10)
| Get the k most similar users for each entry in `users`.
|
| Each type of recommender has its own model for the similarity
| between users. For example, the factorization_recommender will
| return the nearest users based on the cosine similarity
| between latent user factors. (This method is not currently
| available for item_similarity models.)
|
| Parameters
| ----------
| users : SArray or list; optional
| An :class:`~graphlab.SArray` or list of user ids for which to get
| similar users. If 'None', then return the `k` most similar users for
| all users in the training set.
|
| k : int, optional
| The number of neighbors to return for each user.
|
| Returns
| -------
| out : SFrame
| A SFrame with the top ranked similar users for each user. The
| columns `user`, 'similar', 'score' and 'rank', where
| `user` matches the user column name specified at training time.
| The 'rank' is between 1 and `k` and 'score' gives the similarity
| score of that user. The value of the score depends on the method
| used for computing user similarities.
|
| Examples
| --------
|
| >>> sf = graphlab.SFrame({'user_id': ["0", "0", "0", "1", "1", "2", "2", "2"],
| 'item_id': ["a", "b", "c", "a", "b", "b", "c", "d"]})
| >>> m = graphlab.factorization_recommender.create(sf)
| >>> nn = m.get_similar_users()
|
| list_fields(self)
| Get the current settings of the model. The keys depend on the type of
| model.
|
| Returns
| -------
| out : list
| A list of fields that can be queried using the ``get`` method.
|
| predict(self, dataset, new_observation_data=None, new_user_data=None, new_item_data=None)
| Return a score prediction for the user ids and item ids in the provided
| data set.
|
| Parameters
| ----------
| dataset : SFrame
| Dataset in the same form used for training.
|
| new_observation_data : SFrame, optional
| ``new_observation_data`` gives additional observation data
| to the model, which may be used by the models to improve
| score accuracy. Must be in the same format as the
| observation data passed to ``create``. How this data is
| used varies by model.
|
| new_user_data : SFrame, optional
| ``new_user_data`` may give additional user data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the user
| data passed to ``create``.
|
| new_item_data : SFrame, optional
| ``new_item_data`` may give additional item data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the item
| data passed to ``create``.
|
| Returns
| -------
| out : SArray
| An SArray with predicted scores for each given observation
| predicted by the model.
|
| See Also
| --------
| recommend, evaluate
|
| recommend(self, users=None, k=10, exclude=None, items=None, new_observation_data=None, new_user_data=None, new_item_data=None, exclude_known=True, diversity=0, random_seed=None, verbose=True)
| Recommend the ``k`` highest scored items for each user.
|
| Parameters
| ----------
| users : SArray, SFrame, or list, optional
| Users or observation queries for which to make recommendations.
| For list, SArray, and single-column inputs, this is simply a set
| of user IDs. By default, recommendations are returned for all
| users present when the model was trained. However, if the
| recommender model was created with additional features in the
| ``observation_data`` SFrame, then a corresponding SFrame of
| observation queries -- observation data without item or target
| columns -- can be passed to this method. For example, a model
| trained with user ID, item ID, time, and rating columns may be
| queried using an SFrame with user ID and time columns. In this
| case, the user ID column must be present, and all column names
| should match those in the ``observation_data`` SFrame passed to
| ``create.``
|
| k : int, optional
| The number of recommendations to generate for each user.
|
| items : SArray, SFrame, or list, optional
| Restricts the items from which recommendations can be made. If
| ``items`` is an SArray, list, or SFrame with a single column,
| only items from the given set will be recommended. This can be
| used, for example, to restrict the recommendations to items
| within a particular category or genre. If ``items`` is an
| SFrame with user ID and item ID columns, then the item
| restriction is specialized to each user. For example, if
| ``items`` contains 3 rows with user U1 -- (U1, I1), (U1, I2),
| and (U1, I3) -- then the recommendations for user U1 are
| chosen from items I1, I2, and I3. By default, recommendations
| are made from all items present when the model was trained.
|
| new_observation_data : SFrame, optional
| ``new_observation_data`` gives additional observation data
| to the model, which may be used by the models to improve
| score and recommendation accuracy. Must be in the same
| format as the observation data passed to ``create``. How
| this data is used varies by model.
|
| new_user_data : SFrame, optional
| ``new_user_data`` may give additional user data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the user
| data passed to ``create``.
|
| new_item_data : SFrame, optional
| ``new_item_data`` may give additional item data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the item
| data passed to ``create``.
|
| exclude : SFrame, optional
| An :class:`~graphlab.SFrame` of user / item pairs. The
| column names must be equal to the user and item columns of
| the main data, and it provides the model with user/item
| pairs to exclude from the recommendations. These
| user-item-pairs are always excluded from the predictions,
| even if exclude_known is False.
|
| exclude_known : bool, optional
| By default, all user-item interactions previously seen in
| the training data, or in any new data provided using
| new_observation_data.., are excluded from the
| recommendations. Passing in ``exclude_known = False``
| overrides this behavior.
|
| diversity : non-negative float, optional
| If given, then the recommend function attempts chooses a set
| of `k` items that are both highly scored and different from
| other items in that set. It does this by first retrieving
| ``k*(1+diversity)`` recommended items, then randomly
| choosing a diverse set from these items. Suggested values
| for diversity are between 1 and 3.
|
| random_seed : int, optional
| If diversity is larger than 0, then some randomness is used;
| this controls the random seed to use for randomization. If
| None, will be different each time.
|
| verbose : bool, optional
| If True, print the progress of generating recommendation.
|
| Returns
| -------
| out : SFrame
| A SFrame with the top ranked items for each user. The
| columns are: ``user_id``, ``item_id``, *score*,
| and *rank*, where ``user_id`` and ``item_id``
| match the user and item column names specified at training
| time. The rank column is between 1 and ``k`` and gives
| the relative score of that item. The value of score
| depends on the method used for recommendations.
|
| See Also
| --------
| recommend_from_interactions
| predict
| evaluate
|
| recommend_from_interactions(self, observed_items, k=10, exclude=None, items=None, new_user_data=None, new_item_data=None, exclude_known=True, diversity=0, random_seed=None, verbose=True)
| Recommend the ``k`` highest scored items based on the
| interactions given in `observed_items.`
|
| Parameters
| ----------
| observed_items : SArray, SFrame, or list
| A list/SArray of items to use to make recommendations, or
| an SFrame of items and optionally ratings and/or other
| interaction data. The model will then recommend the most
| similar items to those given. If ``observed_items`` has a user
| column, then it must be only one user, and the additional
| interaction data stored in the model is also used to make
| recommendations.
|
| k : int, optional
| The number of recommendations to generate.
|
| items : SArray, SFrame, or list, optional
| Restricts the items from which recommendations can be
| made. ``items`` must be an SArray, list, or SFrame with a
| single column containing items, and all recommendations
| will be made from this pool of items. This can be used,
| for example, to restrict the recommendations to items
| within a particular category or genre. By default,
| recommendations are made from all items present when the
| model was trained.
|
| new_user_data : SFrame, optional
| ``new_user_data`` may give additional user data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the user
| data passed to ``create``.
|
| new_item_data : SFrame, optional
| ``new_item_data`` may give additional item data to the
| model. If present, scoring is done with reference to this
| new information. If there is any overlap with the side
| information present at training time, then this new side
| data is preferred. Must be in the same format as the item
| data passed to ``create``.
|
| exclude : SFrame, optional
| An :class:`~graphlab.SFrame` of items or user / item
| pairs. The column names must be equal to the user and
| item columns of the main data, and it provides the model
| with user/item pairs to exclude from the recommendations.
| These user-item-pairs are always excluded from the
| predictions, even if exclude_known is False.
|
| exclude_known : bool, optional
| By default, all user-item interactions previously seen in
| the training data, or in any new data provided using
| new_observation_data.., are excluded from the
| recommendations. Passing in ``exclude_known = False``
| overrides this behavior.
|
| diversity : non-negative float, optional
| If given, then the recommend function attempts chooses a set
| of `k` items that are both highly scored and different from
| other items in that set. It does this by first retrieving
| ``k*(1+diversity)`` recommended items, then randomly
| choosing a diverse set from these items. Suggested values
| for diversity are between 1 and 3.
|
| random_seed : int, optional
| If diversity is larger than 0, then some randomness is used;
| this controls the random seed to use for randomization. If
| None, then it will be different each time.
|
| verbose : bool, optional
| If True, print the progress of generating recommendation.
|
| Returns
| -------
| out : SFrame
| A SFrame with the top ranked items for each user. The
| columns are: ``item_id``, *score*, and *rank*, where
| ``user_id`` and ``item_id`` match the user and item column
| names specified at training time. The rank column is
| between 1 and ``k`` and gives the relative score of that
| item. The value of score depends on the method used for
| recommendations.
|
| observed_items: list, SArray, or SFrame
|
| show(self, view=None, model_type='recommender')
| show(view=None)
| Visualize a model with GraphLab Create :mod:`~graphlab.canvas`. This function starts Canvas
| if it is not already running. If the Model has already been plotted,
| this function will update the plot.
|
| Parameters
| ----------
| view : str, optional
| The name of the Model view to show. Can be one of:
|
| - Summary: Shows the statistics of the training process such as size of the data and time cost. The summary also shows the parameters and settings for the model training process if available.
| - Evaluation: Shows precision recall plot as line chart. Tooltip is provided for pointwise analysis. Precision recall values are shown in the tooltip at any given cutoff value the mouse points to.
| - Comparison: Shows the precision recall metrics for multiple models. It also support tooltip and highlight (mouse over) and focus (mouse selection on the legend) for inspection in detail.
|
| Returns
| -------
| view : graphlab.canvas.view.View
| An object representing the GraphLab Canvas view.
|
| See Also
| --------
| canvas
|
| Examples
| --------
| Suppose 'm' is a Model, we can view it in GraphLab Canvas using:
|
| >>> m.show()
|
| ----------------------------------------------------------------------
| Data descriptors inherited from graphlab.toolkits.recommender.util._Recommender:
|
| views
| Interactively visualize a recommender model.
|
| Once a model has been trained, you can easily visualize the model. There
| are three built-in visualizations to help explore, explain, and evaluate
| the model.
|
| Examples
| --------
| .. sourcecode:: python
|
| # Show an interactive view
| >>> view = model.views.evaluate(valid)
| >>> view.show()
|
| # Explore predictions
| >>> view = model.views.explore(item_data=items,
| ... item_name_column='movie')
|
| # Explore evals
| >>> view = model.views.overview(
| ... validation_set=valid,
| ... item_data=items,
| ... item_name_column='movie')
| >>> view.show()
|
| See Also
| --------
| graphlab.recommender.util.RecommenderViews
|
| ----------------------------------------------------------------------
| Methods inherited from graphlab.toolkits._model.Model:
|
| __getitem__(self, key)
|
| name(self)
| Returns the name of the model.
|
| Returns
| -------
| out : str
| The name of the model object.
|
| Examples
| --------
| >>> model_name = m.name()
|
| save(self, location)
| Save the model. The model is saved as a directory which can then be
| loaded using the :py:func:`~graphlab.load_model` method.
|
| Parameters
| ----------
| location : string
| Target destination for the model. Can be a local path or remote URL.
|
| See Also
| ----------
| graphlab.load_model
|
| Examples
| ----------
| >>> model.save('my_model_file')
| >>> loaded_model = graphlab.load_model('my_model_file')
|
| ----------------------------------------------------------------------
| Methods inherited from graphlab.toolkits._model.CustomModel:
|
| summary(self, output=None)
| Print a summary of the model. The summary includes a description of
| training data, options, hyper-parameters, and statistics measured
| during model creation.
|
| Parameters
| ----------
| output : str, None
| The type of summary to return.
|
| - None or 'stdout' : print directly to stdout.
|
| - 'str' : string of summary
|
| - 'dict' : a dict with 'sections' and 'section_titles' ordered
| lists. The entries in the 'sections' list are tuples of the form
| ('label', 'value').
|
| Examples
| --------
| >>> m.summary()
|
| ----------------------------------------------------------------------
| Data descriptors inherited from graphlab.toolkits._model.CustomModel:
|
| __dict__
| dictionary for instance variables (if defined)
|
| __weakref__
| list of weak references to the object (if defined)
|
| ----------------------------------------------------------------------
| Methods inherited from graphlab.toolkits._model.ProxyBasedModel:
|
| __dir__(self)
| Combine the results of dir from the current class with the results of
| list_fields().
|
| __getattribute__(self, attr)
| Use the internal proxy object for obtaining list_fields.
|
| ----------------------------------------------------------------------
| Data and other attributes inherited from graphlab.toolkits._model.ProxyBasedModel:
|
| __proxy__ = None
m['coefficients']
{'intercept': 2.875, 'item_id': Columns:
item_id str
linear_terms float
factors array
Rows: 4
Data:
+---------+------------------+-------------------------------+
| item_id | linear_terms | factors |
+---------+------------------+-------------------------------+
| a | -0.0966002643108 | [4.76982750115e-05, -0.002... |
| b | -0.0572980679572 | [-0.00134535413235, -0.003... |
| c | 0.287172853947 | [0.000683953519911, 0.0031... |
| d | -0.601327478886 | [0.000693015812431, 0.0027... |
+---------+------------------+-------------------------------+
[4 rows x 3 columns], 'user_id': Columns:
user_id str
linear_terms float
factors array
Rows: 3
Data:
+---------+-----------------+-------------------------------+
| user_id | linear_terms | factors |
+---------+-----------------+-------------------------------+
| 0 | -1.01640200615 | [-0.000962085323408, -0.00... |
| 1 | 0.842291355133 | [-0.000391170469811, -0.00... |
| 2 | -0.293762326241 | [0.00129368004855, 0.00448... |
+---------+-----------------+-------------------------------+
[3 rows x 3 columns]}
After importing GraphLab Create, we can download data directly from S3. We have placed a preprocessed version of the Million Song Dataset on S3. This data set was used for a Kaggle challenge and includes data from The Echo Nest, SecondHandSongs, musiXmatch, and Last.fm. This file includes data for a subset of 10000 songs.
The CourseTalk dataset: loading and first look¶
Loading of the CourseTalk database.
#train_file = 'http://s3.amazonaws.com/dato-datasets/millionsong/10000.txt'
train_file = '../data/ratings.dat'
sf = graphlab.SFrame.read_csv(train_file, header=False,
delimiter='|', verbose=False)
sf.rename({'X1':'user_id', 'X2':'course_id', 'X3':'rating'}).show()
In order to evaluate the performance of our model, we randomly split the observations in our data set into two partitions: we will use train_set when creating our model and test_set for evaluating its performance.
(train_set, test_set) = sf.random_split(0.8, seed=1)
Popularity model¶
Create a model that makes recommendations using item popularity. When no target column is provided, the popularity is determined by the number of observations involving each item. When a target is provided, popularity is computed using the item’s mean target value. When the target column contains ratings, for example, the model computes the mean rating for each item and uses this to rank items for recommendations.
One typically wants to initially create a simple recommendation system that can be used as a baseline and to verify that the rest of the pipeline works as expected. The recommender package has several models available for this purpose. For example, we can create a model that predicts songs based on their overall popularity across all users.
import graphlab as gl
popularity_model = gl.popularity_recommender.create(train_set, 'user_id', 'course_id', target = 'rating')
Recsys training: model = popularity
Preparing data set.
Data has 2202 observations with 1651 users and 201 items.
Data prepared in: 0.007741s
2202 observations to process; with 201 unique items.
Item similarity Model¶
- Collaborative filtering methods make predictions for a given user based on the patterns of other users' activities. One common technique is to compare items based on their Jaccard similarity.This measurement is a ratio: the number of items they have in common, over the total number of distinct items in both sets.
- We could also have used another slightly more complicated similarity measurement, called Cosine Similarity.
If your data is implicit, i.e., you only observe interactions between users and items, without a rating, then use ItemSimilarityModel with Jaccard similarity.
If your data is explicit, i.e., the observations include an actual rating given by the user, then you have a wide array of options. ItemSimilarityModel with cosine or Pearson similarity can incorporate ratings. In addition, MatrixFactorizationModel, FactorizationModel, as well as LinearRegressionModel all support rating prediction.
Now data contains three columns: ‘user_id’, ‘item_id’, and ‘rating’.¶
itemsim_cosine_model = graphlab.recommender.create(data, target=’rating’, method=’item_similarity’, similarity_type=’cosine’)
factorization_machine_model = graphlab.recommender.create(data, target=’rating’, method=’factorization_model’)
In the following code block, we compute all the item-item similarities and create an object that can be used for recommendations.
item_sim_model = gl.item_similarity_recommender.create(
train_set, 'user_id', 'course_id', target = 'rating',
similarity_type='cosine')
Recsys training: model = item_similarity
Preparing data set.
Data has 2202 observations with 1651 users and 201 items.
Data prepared in: 0.008563s
Training model from provided data.
Gathering per-item and per-user statistics.
+--------------------------------+------------+
| Elapsed Time (Item Statistics) | % Complete |
+--------------------------------+------------+
| 8.764ms | 60.5 |
| 10.998ms | 100 |
+--------------------------------+------------+
Setting up lookup tables.
Processing data in one pass using dense lookup tables.
+-------------------------------------+------------------+-----------------+
| Elapsed Time (Constructing Lookups) | Total % Complete | Items Processed |
+-------------------------------------+------------------+-----------------+
| 11.753ms | 0 | 0 |
| 22.738ms | 100 | 201 |
+-------------------------------------+------------------+-----------------+
Finalizing lookup tables.
Generating candidate set for working with new users.
Finished training in 0.026708s
Factorization Recommender Model¶
Create a FactorizationRecommender that learns latent factors for each user and item and uses them to make rating predictions. This includes both standard matrix factorization as well as factorization machines models (in the situation where side data is available for users and/or items). link
factorization_machine_model = gl.recommender.factorization_recommender.create(
train_set, 'user_id', 'course_id',
target='rating')
Recsys training: model = factorization_recommender
Preparing data set.
Data has 2202 observations with 1651 users and 201 items.
Data prepared in: 0.008281s
Training factorization_recommender for recommendations.
+--------------------------------+--------------------------------------------------+----------+
| Parameter | Description | Value |
+--------------------------------+--------------------------------------------------+----------+
| num_factors | Factor Dimension | 8 |
| regularization | L2 Regularization on Factors | 1e-08 |
| solver | Solver used for training | sgd |
| linear_regularization | L2 Regularization on Linear Coefficients | 1e-10 |
| max_iterations | Maximum Number of Iterations | 50 |
+--------------------------------+--------------------------------------------------+----------+
Optimizing model using SGD; tuning step size.
Using 2202 / 2202 points for tuning the step size.
+---------+-------------------+------------------------------------------+
| Attempt | Initial Step Size | Estimated Objective Value |
+---------+-------------------+------------------------------------------+
| 0 | 25 | Not Viable |
| 1 | 6.25 | Not Viable |
| 2 | 1.5625 | Not Viable |
| 3 | 0.390625 | 0.104061 |
| 4 | 0.195312 | 0.177274 |
| 5 | 0.0976562 | 0.235698 |
+---------+-------------------+------------------------------------------+
| Final | 0.390625 | 0.104061 |
+---------+-------------------+------------------------------------------+
Starting Optimization.
+---------+--------------+-------------------+-----------------------+-------------+
| Iter. | Elapsed Time | Approx. Objective | Approx. Training RMSE | Step Size |
+---------+--------------+-------------------+-----------------------+-------------+
| Initial | 43us | 0.891401 | 0.94414 | |
+---------+--------------+-------------------+-----------------------+-------------+
| 1 | 26.868ms | 0.905107 | 0.951369 | 0.390625 |
| 2 | 66.335ms | 0.487535 | 0.698236 | 0.232267 |
| 3 | 107.56ms | 0.306843 | 0.553933 | 0.171364 |
| 4 | 149.729ms | 0.218669 | 0.46762 | 0.116134 |
| 5 | 188.297ms | 0.16658 | 0.408142 | 0.098237 |
| 6 | 227.317ms | 0.125822 | 0.354713 | 0.0856819 |
| 11 | 411.924ms | 0.0426793 | 0.206587 | 0.0543824 |
| 25 | 923.563ms | 0.00689808 | 0.0830431 | 0.0293797 |
| 50 | 1.89s | 0.00175875 | 0.0419116 | 0.0174693 |
+---------+--------------+-------------------+-----------------------+-------------+
Optimization Complete: Maximum number of passes through the data reached.
Computing final objective value and training RMSE.
Final objective value: 0.00157196
Final training RMSE: 0.0396206
Model Evaluation¶
It's straightforward to use GraphLab to compare models on a small subset of users in the test_set. The precision-recall plot that is computed shows the benefits of using the similarity-based model instead of the baseline popularity_model: better curves tend toward the upper-right hand corner of the plot.
The following command finds the top-ranked items for all users in the first 500 rows of test_set. The observations in train_set are not included in the predicted items.
result = gl.recommender.util.compare_models(
test_set, [popularity_model, item_sim_model, factorization_machine_model],
user_sample=.5, skip_set=train_set)
compare_models: using 246 users to estimate model performance
PROGRESS: Evaluate model M0
Precision and recall summary statistics by cutoff
+--------+-------------------+------------------+
| cutoff | mean_precision | mean_recall |
+--------+-------------------+------------------+
| 1 | 0.0 | 0.0 |
| 2 | 0.0 | 0.0 |
| 3 | 0.0 | 0.0 |
| 4 | 0.0 | 0.0 |
| 5 | 0.0 | 0.0 |
| 6 | 0.0 | 0.0 |
| 7 | 0.0 | 0.0 |
| 8 | 0.0 | 0.0 |
| 9 | 0.000451671183379 | 0.00406504065041 |
| 10 | 0.000406504065041 | 0.00406504065041 |
+--------+-------------------+------------------+
[10 rows x 3 columns]
('\nOverall RMSE: ', 0.802748145173018)
Per User RMSE (best)
+---------+-------+------+
| user_id | count | rmse |
+---------+-------+------+
| 1491 | 1 | 0.0 |
+---------+-------+------+
[1 rows x 3 columns]
Per User RMSE (worst)
+---------+-------+---------------+
| user_id | count | rmse |
+---------+-------+---------------+
| 669 | 1 | 3.91346153846 |
+---------+-------+---------------+
[1 rows x 3 columns]
Per Item RMSE (best)
+-----------+-------+------+
| course_id | count | rmse |
+-----------+-------+------+
| 37 | 1 | 0.0 |
+-----------+-------+------+
[1 rows x 3 columns]
Per Item RMSE (worst)
+-----------+-------+---------------+
| course_id | count | rmse |
+-----------+-------+---------------+
| 144 | 2 | 2.68451721042 |
+-----------+-------+---------------+
[1 rows x 3 columns]
PROGRESS: Evaluate model M1
Precision and recall summary statistics by cutoff
+--------+------------------+------------------+
| cutoff | mean_precision | mean_recall |
+--------+------------------+------------------+
| 1 | 0.00813008130081 | 0.00813008130081 |
| 2 | 0.00813008130081 | 0.0162601626016 |
| 3 | 0.00677506775068 | 0.0172764227642 |
| 4 | 0.00609756097561 | 0.0182926829268 |
| 5 | 0.00650406504065 | 0.0264227642276 |
| 6 | 0.00609756097561 | 0.030487804878 |
| 7 | 0.00638792102207 | 0.0386178861789 |
| 8 | 0.00660569105691 | 0.0440379403794 |
| 9 | 0.0063233965673 | 0.0481029810298 |
| 10 | 0.00609756097561 | 0.050135501355 |
+--------+------------------+------------------+
[10 rows x 3 columns]
('\nOverall RMSE: ', 4.557516953416079)
Per User RMSE (best)
+---------+-------+----------------+
| user_id | count | rmse |
+---------+-------+----------------+
| 2017 | 1 | 0.495458717346 |
+---------+-------+----------------+
[1 rows x 3 columns]
Per User RMSE (worst)
+---------+-------+------+
| user_id | count | rmse |
+---------+-------+------+
| 1704 | 1 | 5.0 |
+---------+-------+------+
[1 rows x 3 columns]
Per Item RMSE (best)
+-----------+-------+----------------+
| course_id | count | rmse |
+-----------+-------+----------------+
| 214 | 1 | 0.495458717346 |
+-----------+-------+----------------+
[1 rows x 3 columns]
Per Item RMSE (worst)
+-----------+-------+------+
| course_id | count | rmse |
+-----------+-------+------+
| 47 | 1 | 5.0 |
+-----------+-------+------+
[1 rows x 3 columns]
PROGRESS: Evaluate model M2
Precision and recall summary statistics by cutoff
+--------+------------------+------------------+
| cutoff | mean_precision | mean_recall |
+--------+------------------+------------------+
| 1 | 0.00406504065041 | 0.00406504065041 |
| 2 | 0.00609756097561 | 0.00691056910569 |
| 3 | 0.00406504065041 | 0.00691056910569 |
| 4 | 0.00508130081301 | 0.0123306233062 |
| 5 | 0.00650406504065 | 0.0218157181572 |
| 6 | 0.00542005420054 | 0.0218157181572 |
| 7 | 0.00464576074332 | 0.0218157181572 |
| 8 | 0.00406504065041 | 0.0218157181572 |
| 9 | 0.00361336946703 | 0.0218157181572 |
| 10 | 0.00325203252033 | 0.0218157181572 |
+--------+------------------+------------------+
[10 rows x 3 columns]
('\nOverall RMSE: ', 0.8528125702102667)
Per User RMSE (best)
+---------+-------+------------------+
| user_id | count | rmse |
+---------+-------+------------------+
| 1526 | 1 | 0.00659944340384 |
+---------+-------+------------------+
[1 rows x 3 columns]
Per User RMSE (worst)
+---------+-------+---------------+
| user_id | count | rmse |
+---------+-------+---------------+
| 669 | 1 | 3.90590791181 |
+---------+-------+---------------+
[1 rows x 3 columns]
Per Item RMSE (best)
+-----------+-------+------------------+
| course_id | count | rmse |
+-----------+-------+------------------+
| 129 | 1 | 0.00681198910081 |
+-----------+-------+------------------+
[1 rows x 3 columns]
Per Item RMSE (worst)
+-----------+-------+---------------+
| course_id | count | rmse |
+-----------+-------+---------------+
| 122 | 2 | 3.47816843841 |
+-----------+-------+---------------+
[1 rows x 3 columns]
Now let's ask the item similarity model for song recommendations on several users. We first create a list of users and create a subset of observations, users_ratings, that pertain to these users.
K = 10
users = gl.SArray(sf['user_id'].unique().head(100))
users
dtype: int Rows: 100 [232, 363, 431, 738, 1860, 732, 187, 1368, 1753, 764, 926, 1180, 1323, 1742, 1685, 1876, 1232, 614, 1573, 786, 1158, 1072, 863, 695, 454, 1211, 1404, 1242, 696, 444, 349, 1883, 499, 354, 573, 1531, 71, 1889, 312, 578, 1556, 1572, 79, 416, 848, 1805, 550, 1644, 1017, 521, 566, 703, 196, 1401, 533, 1054, 398, 1077, 341, 982, 516, 1473, 1982, 1670, 529, 1544, 1920, 1414, 223, 465, 376, 1231, 193, 202, 1128, 1853, 1907, 1331, 966, 810, 1895, 1704, 267, 1615, 350, 979, 69, 138, 1645, 837, 1841, 1801, 853, 803, 405, 1172, 112, 1653, 937, 1429]
Next we use the recommend() function to query the model we created for recommendations. The returned object has four columns: user_id, song_id, the score that the algorithm gave this user for this song, and the song's rank (an integer from 0 to K-1). To see this we can grab the top few rows of recs:
recs = item_sim_model.recommend(users=users, k=K)
recs.head()
| user_id | course_id | score | rank |
|---|---|---|---|
| 232 | 93 | 0.219596922398 | 1 |
| 232 | 180 | 0.212747454643 | 2 |
| 232 | 188 | 0.201870501041 | 3 |
| 232 | 108 | 0.178093016148 | 4 |
| 232 | 55 | 0.175357162952 | 5 |
| 232 | 168 | 0.167150199413 | 6 |
| 232 | 133 | 0.16673386097 | 7 |
| 232 | 186 | 0.161530077457 | 8 |
| 232 | 164 | 0.160108804703 | 9 |
| 232 | 187 | 0.157858431339 | 10 |
To learn what songs these ids pertain to, we can merge in metadata about each song.
# Get the meta data of the courses
courses = gl.SFrame.read_csv('../data/cursos.dat', header=False, delimiter='|', verbose=False)
courses.rename({'X1':'course_id', 'X2':'title', 'X3':'avg_rating',
'X4':'workload', 'X5':'university', 'X6':'difficulty', 'X7':'provider'}).show()
courses = courses[['course_id', 'title', 'provider']]
results = recs.join(courses, on='course_id', how='inner')
#Populate observed user-course data with course info
userset = frozenset(users)
ix = sf['user_id'].apply(lambda x: x in userset, int)
user_data = sf[ix]
user_data = user_data.join(courses, on='course_id')[['user_id', 'title', 'provider']]
# Print out some recommendations
for i in range(5):
user = list(users)[i]
print "User: " + str(i + 1)
user_obs = user_data[user_data['user_id'] == user].head(K)
del user_obs['user_id']
user_recs = results[results['user_id'] == str(user)][['title', 'provider']]
print "We were told that the user liked these courses: "
print user_obs.head(K)
print "We recommend these other courses:"
print user_recs.head(K)
print ""
User: 1 We were told that the user liked these courses: +-------------------------------+----------+ | title | provider | +-------------------------------+----------+ | An Introduction to Interac... | coursera | +-------------------------------+----------+ [1 rows x 2 columns] We recommend these other courses: +-------+----------+ | title | provider | +-------+----------+ +-------+----------+ [0 rows x 2 columns] User: 2 We were told that the user liked these courses: +-------------------------------+----------+ | title | provider | +-------------------------------+----------+ | An Introduction to Interac... | coursera | +-------------------------------+----------+ [1 rows x 2 columns] We recommend these other courses: +-------+----------+ | title | provider | +-------+----------+ +-------+----------+ [0 rows x 2 columns] User: 3 We were told that the user liked these courses: +-------------------------------+----------+ | title | provider | +-------------------------------+----------+ | An Introduction to Interac... | coursera | +-------------------------------+----------+ [1 rows x 2 columns] We recommend these other courses: +-------+----------+ | title | provider | +-------+----------+ +-------+----------+ [0 rows x 2 columns] User: 4 We were told that the user liked these courses: +-------------------------------+----------+ | title | provider | +-------------------------------+----------+ | A Beginner's Guide to ... | coursera | | Gamification | coursera | +-------------------------------+----------+ [2 rows x 2 columns] We recommend these other courses: +-------+----------+ | title | provider | +-------+----------+ +-------+----------+ [0 rows x 2 columns] User: 5 We were told that the user liked these courses: +-------------------------------+----------+ | title | provider | +-------------------------------+----------+ | Web Intelligence and Big Data | coursera | +-------------------------------+----------+ [1 rows x 2 columns] We recommend these other courses: +-------+----------+ | title | provider | +-------+----------+ +-------+----------+ [0 rows x 2 columns]
