%pylab inline
# shouldn't be needed if you started the server with `ipython notebook --pylab inline` but otherwise...
Welcome to pylab, a matplotlib-based Python environment [backend: module://IPython.zmq.pylab.backend_inline]. For more information, type 'help(pylab)'.
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['image.interpolation']= 'nearest'
0. Introduction and basics¶
Github Repo for IPython Notebook¶
http://github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy
on the command line: git clone http://github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy
then: cd pydata_bos_2013_intro_to_numpy
finally: ipython notebook --pylab inline
Who am I?¶
Contact Info¶
* Andrew Giessel * twitter: @giessel * github: @andrewgiessel * email: andrew_giessel@hms.harvard.edu * web: http://giessel.com
Postdoctoral fellow at HMS, Datta Lab, http://dattalab.org
Plug: See my talk tomorrow!
What do I use NumPy for?¶
- images and image series
<img src='https://raw.github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy/master/neurons.png', height='512'>
- electrophysiology data
<img src='https://raw.github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy/master/action_potentials.png', width='512'>
- data analysis
<img src='https://raw.github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy/master/marked_neurons.png', width='512'>
<img src='https://raw.github.com/andrewgiessel/pydata_bos_2013_intro_to_numpy/master/IAA_pca.png', width='512')
- simultations
ODE/PDE models and their data
1. Core data structure: np.ndarray¶
- contigious block of memory which stores a collection of data (generally numeric)
- compact memory representation--- not a list of pointers to python objects (ints)

- each element of the collection has the same data type (signed integer, floats, unsigned integers, booleans)
- array is a python object which is a view on this section of memory
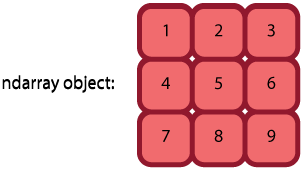
- Attributes
- data - memory location
- shape - size of each dimension (3,3)
- strides - how to move in memory for each dimension (row to row, column to column) (3, 1)
- dtype - data type of the elements - affects the size of the stride and the shape
The ndarray object allows for different views (sub sections, reshaping, transposition, etc) without actually changing anything in memory- just the interpretation of the stored memory changes.
All interfaces with this data structure are written in C and accessing/modifying the data structures are therefore fast
2. Array construction¶
import numpy as np
# np.array() - takes a list or tuple and makes an array. core creation function
A = np.array([1, 2, 3, 4, 5])
A
array([1, 2, 3, 4, 5])
B = np.array([[5.,6.,7.],[8.,9.,10.]])
print B
[[ 5. 6. 7.] [ 8. 9. 10.]]
plt.figure()
plt.plot(A, 'o', ls='')
plt.figure()
plt.imshow(B)
plt.colorbar()
<matplotlib.colorbar.Colorbar instance at 0x114f0af38>
# np.arange() - works like range()
np.arange(5)
array([0, 1, 2, 3, 4])
np.arange(2,30,4) # 2 to 30, every 4th value
array([ 2, 6, 10, 14, 18, 22, 26])
# np.zeros(), np.ones(), np.empty() - take a tuple, each entry is the size in that dimension
A = np.zeros((4,10))
B = np.ones((15,2))
C = np.empty((5))
A, B, C
(array([[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]),
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.],
[ 1., 1.]]),
array([ -0.00000000e+000, -2.00000013e+000, 2.12274051e-314,
2.30109990e-314, 2.13292407e-314]))
# np.zeros_like(), np.ones_like(), np.empty_like() - take their shape from what you pass in
# note that this also uses the datatype of the array, as well
B_2 = np.ones_like(A)
A, B_2
(array([[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]),
array([[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]]))
see also: np.tile(), np.r_(), np.c_(), np.linspace(), np.random.random(), np.fromfile(), np.genfromtxt()¶
3. Arrray Indexing, Manipulation and Attributes¶
3.1 Array Indexing¶
Indexing is pythonic and very similar to lists- for a review of slice indexing of strings (and lists) here:
http://docs.python.org/2/tutorial/introduction.html#strings
In sort, they are accessed like lists, using slices for each dimension. Like lists and strings, they use 0-based indexing.
A = np.random.random((10,10))
plt.imshow(A)
plt.colorbar()
A[0,0]
0.46927082670852238
# and assignment obviously works
A[0,0] = 1.0
plt.imshow(A)
plt.colorbar()
<matplotlib.colorbar.Colorbar instance at 0x11742eab8>
# using slices to get part of an array
# the notation is start:stop:interval, once for each dimension
# if you leave off a slice, numpy assumes you mean all of the remaining dimensions
plt.plot(A[:,0])
figure()
plt.imshow(A[:5,:])
<matplotlib.image.AxesImage at 0x1187bd810>
3.2 Iterating over NumPy arrays¶
It should be noted that iterating over NumPy arrays can in many cases be avoided all together (see below). But they are iterators, and return slices of the array relative to the first axis. If 1d, this is much like a list
for item in np.array([1,3,5,7,9]):
print item
1 3 5 7 9
A = np.random.random((2,10))
for i in A:
print i
[ 0.11701571 0.46056106 0.01030415 0.10114525 0.54354656 0.69549508 0.98440174 0.1424281 0.05723334 0.21373704] [ 0.85163565 0.3325828 0.59396438 0.17541558 0.98426345 0.97172212 0.90464501 0.91477527 0.59878944 0.45344777]
# we can temporarily switch the axis to iterate over with np.rollaxis(), see below
# alternatively you can get the shape of the array and use those as loop variables.
3.3 Array Attributes¶
ndarrays have many methods and attributes. Of particular note here .shape, .dtype, and .ndim
A = np.arange(25).reshape(5,5)
print A.shape # tuple of dimension sizes, I use this one constantly
print A.ndim # equal to len(asdf.shape)
print A.dtype # default on my platform is 64bit int
print A.size # total number of elements in the array
(5, 5) 2 int64 25
3.4 Array Manipulation¶
There are many routines to manipulate and alter properties of NumPy arrays. Many are methods on ndarrays, and some are redundently defined as module level NumPy functions. Here are a handful of the ones I end up using the most.
# .copy() - return a copy of an array, not a view. also is a method on an ndarray object
A = np.array([1,2,3,4])
B = A.copy() # or - np.copy(asdf)
B[0] = 99
A, B
(array([1, 2, 3, 4]), array([99, 2, 3, 4]))
# .reshape() - takes an array and a tuple of the new size to change that array to
# and returns a view on the *same array*
A = np.array([1,2,3,4])
print A
print
B = A.reshape((2,2))
print B
print
B[0,0] = 9
print A
[1 2 3 4] [[1 2] [3 4]] [9 2 3 4]
# .astype() - casting method, can use built-in data types, a host of datatypes includined in NumPy, or strings
A = np.array([0,1,2,3,4])
print A.astype(float)
print A.astype(bool) # 0 is False, >0 is True
B = np.array([0.1,0.2,0.3,0.4,0.5])
print B.astype(int) # note the floor
C = np.array([-4,-3,-2,-1,0,1,2,3,4]).astype('uint16')
print C # note wraparound
# finally, note that astype() returns a casted COPY of the array
[ 0. 1. 2. 3. 4.] [False True True True True] [0 0 0 0 0] [65532 65533 65534 65535 0 1 2 3 4]
For more info about data types in NumPy see: http://docs.scipy.org/doc/numpy/reference/arrays.dtypes.html
# np.roll() - rotate the data along a given axis, returns a copy
A = np.array([1,2,3,4])
B = np.roll(A, 1)
print A, B
print '---------'
A = A.reshape((2,2))
C = np.roll(A, 1, axis=0)
D = np.roll(A, 1, axis=1)
print A
print
print C
print
print D
[1 2 3 4] [4 1 2 3] --------- [[1 2] [3 4]] [[3 4] [1 2]] [[2 1] [4 3]]
# .T - transpose method on an ndarray, returns a view on the original array
# unlike the others listed here, this is an attribute, not a method
A = np.arange(25).reshape(5,5)
print A
print
print A.T
print
print A.T[4,0]
A.T[4,0] = 99
print
print A[4,0]
[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24]] [[ 0 5 10 15 20] [ 1 6 11 16 21] [ 2 7 12 17 22] [ 3 8 13 18 23] [ 4 9 14 19 24]] 4 20
# np.rollaxis() - reorder axes in an array, returning a view
# takes an array, the axis to reorder, and the position to roll before.
# the relative order of the other axes are not changed
A = np.zeros((2,3,4))
B = np.rollaxis(A, 2, 0)
print A.shape, B.shape
print '---------'
B[0,0,0] = 1
print A
(2, 3, 4) (4, 2, 3) --------- [[[ 1. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]]]
# note that we can use rollaxis with iteration to get a slices of an array in a given dimension
# simply roll that axes to the start
A = np.zeros((2,3,4))
for array_slice in np.rollaxis(A,2,0):
print array_slice.shape
(2, 3) (2, 3) (2, 3) (2, 3)
# np.unique() - like set, but for ndarrays:
A = np.array([1,1,3,4,5,0])
print np.unique(A)
[0 1 3 4 5]
# .flatten() - return a copy of an multidimensional array flattened into one dimension
# compart to .flat - an attribute which is a 1d iterator over the whole array
A = np.arange(25).reshape(5,5)
B = A.flatten()
A, B
(array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]]),
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24]))
# .tolist() - convert an ndarray to a list - works for multidimensonial arrays
A = np.arange(25).reshape(5,5)
print A.tolist()
[[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19], [20, 21, 22, 23, 24]]
4. Array based Calcuations¶
4.1 Array operations are element-by-element, Broadcasting¶
NdArrays can added, subtracted, multiplied and divided using +,-,, and /. Operations done this way are on an element by element basis. Note that is not matrix multiplication, it is element by element multiplication.
A = np.ones((5,5))
print A
print
print A+A
print
print A*A # 1*1 = 1!
print
print np.dot(A, A) # multiple matrices with np.dot
[[ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.]] [[ 2. 2. 2. 2. 2.] [ 2. 2. 2. 2. 2.] [ 2. 2. 2. 2. 2.] [ 2. 2. 2. 2. 2.] [ 2. 2. 2. 2. 2.]] [[ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.]] [[ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.]]
Fundamentally, two arrays must be the exact same shape to do element-by-element operations. However, we can also combine arrays of slightly different shapes by "broadcasting" the smaller array to an appropriate shape. For instance, this is how one would multiply a matrix by a scalar- the scalar is broadcast to the appropriate shape first
print A
print
print A*5
[[ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.] [ 1. 1. 1. 1. 1.]] [[ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.] [ 5. 5. 5. 5. 5.]]
Broadcasting can be tricky to wrap your head around, but generally it just works-- although, you might have to transpose arrays from time to time.
When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing dimensions, and works its way forward. Two dimensions are compatible when
- they are equal, or
- one of them is 1
See the http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html for more details.
4.2 Summary statistics and other functions¶
In fact, most functions on ndarrays are 'universal functions', or 'ufuncs' for short. These are functions, generally written in C, which operate on ndarrays in an element-by-element manner. One might think about them as something like list comprehensions, but they are specific to ndarrays and handle broadcasting, casting, etc. In addition to the general operations above, there are things like sine, cosine, greater-than, etc.
For more information on unfuncs, see here: http://docs.scipy.org/doc/numpy/reference/ufuncs.html
Now I'll show you some of the functions in the NumPy API that I use most often.
A note- many of the functions that follow take the axis keyword. This means that the function is calculated over that specific axis. If this is left off, then the function is calculated on a flattened version of the array. Most of these functions are methods on ndarrays as well as functions in the numpy namespace itself.
# np.sum(), .sum() - calculate the sum of the elements over a given axes, returning a new array
A = np.arange(25).reshape(5,5)
print A
print
print A.sum()
print
print A.sum(axis=0)
print
print A.sum(axis=1)
[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24]] 300 [50 55 60 65 70] [ 10 35 60 85 110]
# np.mean(), .mean() - calcuated the average of elements over a given axis, returning a new array
A = np.arange(25).reshape(5,5)
print A
print
print A.mean()
print
print A.mean(axis=0)
print
print A.mean(axis=1)
[[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24]] 12.0 [ 10. 11. 12. 13. 14.] [ 2. 7. 12. 17. 22.]
See also: np.std(), np.median(), np.min() and np.max()
# np.argmin(), .argmin(), np.argmax(), .argmax(), - return the index of the mininum or maximum value in the array
# note that these take the axis keyword- otherwise they return the max of the flattened array
# see also .argwhere()
A = np.arange(25)
B = A.reshape(5,5)
print A
print
print B
print np.argmin(A)
print
print np.argmax(B, axis=1)
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24] [[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19] [20 21 22 23 24]] 0 [4 4 4 4 4]
# np.ceil, np.floor, np.round - rounding operations, element-wise
A = np.random.random((10,10)) # create an array of random numbers between 0 and 1
A_ceil = np.ceil(A)
A_floor = np.floor(A)
A_round = np.round(A)
figure(figsize=(12,16))
subplot(1,4,1)
imshow(A)
subplot(1,4,2)
imshow(A_ceil, vmin=0, vmax=1)
subplot(1,4,3)
imshow(A_floor)
subplot(1,4,4)
imshow(A_round)
<matplotlib.image.AxesImage at 0x115e5d410>
# np.dot - dot product. works for vectors and matrices - for 2d matricies it is the matrix product
A = [[1, 0], [0, 1]]
B = [[4, 1], [2, 2]]
print np.dot(A, B)
[[4 1] [2 2]]
# np.exp(), np.log(), np.power(), calculate exponential, log, and power functions on an element by element basis
A = np.arange(10)
print A
print
print np.log(A)
print
print np.power(A, 2) # second argument is the power function -- can be another array!
print
print np.exp(A+1)
[0 1 2 3 4 5 6 7 8 9] [ -inf 0. 0.69314718 1.09861229 1.38629436 1.60943791 1.79175947 1.94591015 2.07944154 2.19722458] [ 0 1 4 9 16 25 36 49 64 81] [ 2.71828183e+00 7.38905610e+00 2.00855369e+01 5.45981500e+01 1.48413159e+02 4.03428793e+02 1.09663316e+03 2.98095799e+03 8.10308393e+03 2.20264658e+04]
# np.diff - discrete difference
# note: has an axis argument
A = np.arange(25)
A[12:] += 10
plot(A, label='data')
plot(np.diff(A), label='first difference')
legend()
<matplotlib.legend.Legend at 0x115b85790>
Although strictly speaking not part of NumPy, scipy has a module for different forms of numerical integration - see scipy.integrate.trapz() for example
5. Advanced Indexing and other NumPy built-ins¶
5.1 Advanced Indexing¶
In addition to slices, NumPy supports several other indexing methods, some of which are similar to MATLAB. These can be very powerful. In general, one can use another ndarray object (or even a list/tuple, which will be cast to an ndarray) as an index in any of the dimensions.
A = np.arange(10,0,-1) # make a reverse list
print A[[1,5,7]]
[9 5 3]
Another common use is to use a boolean array of the same size as one or more of the dimensions of the original array to pick the indices we care about. Because many operations on NumPy arrays return truth on an element by element basis, we can combine these quite powerfully.
A = np.arange(100).reshape(10,10)
index = A > 30
print A[index]
print A[index].shape
imshow(A)
figure()
imshow(index)
[31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99] (69,)
<matplotlib.image.AxesImage at 0x116318610>
Boolean indexing is most natural when the boolean array is the same size as the array you're working with, but it can also address a subset of dimensions.
A = np.random.random((100,100,100)) * np.arange(100) # 100 frames of increasing random numbers
figure()
subplot(1,3,1)
imshow(A[:,:,0], vmax=100)
subplot(1,3,2)
imshow(A[:,:,50], vmax=100)
subplot(1,3,3)
imshow(A[:,:,99], vmax=100)
index = np.zeros((100,100), dtype=bool)
index[50:65,50:60] = True
print A[index,:].shape
figure()
imshow(index)
figure()
plot(A[index,:].mean(axis=0))
(150, 100)
[<matplotlib.lines.Line2D at 0x1166fdad0>]
There are a lot of helpful boolean logic NumPy functions that can let you manipulate boolean indices:
- np.logical_not()
- np.logical_and()
- np.logical_or()
- np.logical_xor()
And finally, in addition to just doing <, >, etc., there are some built-in functions that return boolean arrays suitable for indexing, such as:
- np.isnan()
- np.isreal()
- np.isinf()
For more information on indexing, this section is worth some study http://wiki.scipy.org/Tentative_NumPy_Tutorial#head-0dffc419afa7d77d51062d40d2d84143db8216c2
5.2 Other NumPy Builtins¶
There are several methods for array concatenation and spliting, 3 for the first three dimensions, and one for combining over any dimension
- np.hstack(), np.hsplit()
- np.vstack(), np.vsplit()
- np.dstack(), np.dsplit()
- np.concatenate
Finally, I'll mention some useful misc. functions.
- np.atleast_2d(), np.atleast_3d() - adds empty dimensions to an array to get it to at least 2 or 3d. Useful for broadcasting
- np.histogram() - generates bins and counts for histograms. I tend to use matplotlib for histograms but this can be good to get the values
- np.genfromtxt() - a fast text parser. Pandas is far more flexible, but for most .csv files, this will work great
6. Other NumPy libraries¶
6.1 Random¶
NumPy has a submodule called 'random' that lets one generate a lot of arrays of random numbers. We've already seen my default - np.random.random()
# np.random.random() - takes a tuple that is the shape of the array (like np.zeros()) and files with with random floats on the interval [0.0, 1.0)
# note that if you call it with no arguments, it returns a single number, of type 'float'
A = np.random.random(5)
B = np.random.random((5,5))
print A
print
print B
[ 0.12696198 0.53462711 0.35026549 0.93054381 0.8217209 ] [[ 0.68204443 0.25616553 0.65095089 0.28894131 0.98159034] [ 0.26287008 0.69991753 0.67039299 0.36662947 0.41593416] [ 0.86577548 0.67656145 0.58054953 0.13957687 0.97708813] [ 0.22748499 0.51708836 0.50054294 0.59994996 0.43973479] [ 0.62321851 0.91584399 0.79006355 0.17133623 0.76340225]]
If you want to set the random generator so that it isn't so... random, you can use np.random.seed(). Good for having test code that doesn't change but is drawn from a random distribution.
# np.random.seed()
for i in range(10):
np.random.seed(0)
print np.random.random()
0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927 0.548813503927
# np.random.randint() is different- it returns a specified number of random integers in your specified interval
for i in range(10):
print np.random.randint(0,7) # dice roll! (note that the high value is exclusive) # randomintegers() is inclusive
print
# if you want a collection of them, you use the 'size' keyword
print np.random.randint(0,7,10)
5 0 3 3 3 1 3 5 2 4 [6 0 0 4 2 1 6 6 0 1]
np.random.shuffle() is a convienent way to randomize an array that you've already created. Note that it modifies in place! np.random.permutation() returns a shuffled view on the data.
A = np.arange(15)
print A
print
np.random.shuffle(A)
print A
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14] [10 1 6 7 2 12 14 11 0 3 4 13 8 9 5]
There are a number of distributions built into NumPy that you can sample, they all have various parameters and a 'size' keyword.
# np.random.normal() - takes mean, std, and # of samples
for i in [10,100,1000,10000,100000]:
figure()
plt.hist(np.random.normal(5, 5, i))
There are many others - binomial, multivariate, poisson, power, etc. See http://docs.scipy.org/doc/numpy/reference/routines.random.html for a complete list
6.2 Linear Algebra¶
np.linalg is a NumPy submodule with many standard linear algebra routines.
# solve for Ax = b
A = np.array([[1,2], [-1,1]])
b = np.array([1,1])
x = np.linalg.solve(A,b)
print x
[-0.33333333 0.66666667]
A = np.random.randint(0, 10, 25).reshape(5, 5)
print A
e_vals, e_vecs = np.linalg.eig(A)
print
print e_vals
print e_vecs
[[9 8 5 7 0] [4 3 7 1 4] [2 5 1 0 0] [1 9 6 1 9] [0 7 9 1 6]] [ 19.08863964+0.j 3.85846812+3.66977644j 3.85846812-3.66977644j -3.40278794+1.08975429j -3.40278794-1.08975429j] [[-0.70154094+0.j -0.31209910-0.40197915j -0.31209910+0.40197915j 0.34872346+0.16574551j 0.34872346-0.16574551j] [-0.36990076+0.j -0.06325480+0.0579489j -0.06325480-0.0579489j 0.23805294-0.30985306j 0.23805294+0.30985306j] [-0.17981373+0.j -0.21144924+0.0915727j -0.21144924-0.0915727j -0.46851152+0.16062818j -0.46851152-0.16062818j] [-0.45990272+0.j 0.66330367+0.j 0.66330367+0.j -0.58109013+0.j -0.58109013+0.j ] [-0.35660937+0.j 0.44956891+0.196131j 0.44956891-0.196131j 0.31980954+0.11399083j 0.31980954-0.11399083j]]
6.3 FFT¶
# example stolen from http://glowingpython.blogspot.com/2011/08/how-to-plot-frequency-spectrum-with.html
figure(figsize=(12,8))
def plotSpectrum(y,Fs):
"""
Plots a Single-Sided Amplitude Spectrum of y(t)
"""
n = len(y) # length of the signal
k = np.arange(n)
T = n/Fs
frq = k/T # two sides frequency range
frq = frq[range(n/2)] # one side frequency range
Y = np.fft.fft(y)/n # fft computing and normalization
Y = Y[range(n/2)]
plot(frq,abs(Y),'r') # plotting the spectrum
xlabel('Freq (Hz)')
ylabel('|Y(freq)|')
Fs = 150.0; # sampling rate
Ts = 1.0/Fs; # sampling interval
t = np.arange(0,1,Ts) # time vector
ff = 5; # frequency of the signal
y = np.sin(2*np.pi*ff*t)
subplot(2,1,1)
plot(t,y)
xlabel('Time')
ylabel('Amplitude')
subplot(2,1,2)
plotSpectrum(y,Fs)
6.4 Polynomials¶
Polynomials are handled in the polynomial submodule of NumPy.
# polynomials have their own convience classes, you pass in the coefficents.
# the degree is infered from the length of the coefficent list.
p = np.polynomial.Polynomial([5,1,1])
# we can evaluate at a point or over a range of values
print p(3)
plot(np.arange(0,10,0.01), p(np.arange(0,10,0.01)))
xlabel('x')
ylabel('y')
17.0
<matplotlib.text.Text at 0x116726410>
We can also fit data to a polynomial of a given degree, which uses the least squares routine to find the best values for the coefficients.
# let's cheat and use the polynomial function to make some data for us
x_vals = np.arange(0,10,0.01)
p = np.polynomial.Polynomial([5,1,1])
clean_data = p(x_vals)
num_points = clean_data.shape[0]
dirty_data = clean_data + (np.random.random(num_points) * 10 - 5) # now dirty_data is clean data +/- 5
fit_coefs = np.polynomial.polynomial.polyfit(x_vals, dirty_data, 2) # takes x values, y values and the degree to try and fit the data to
print fit_coefs
fit_p = np.polynomial.Polynomial(fit_coefs) # now build a polynomial with those fit values
# plot them
plot(x_vals, dirty_data, label='dirty data')
plot(x_vals, fit_p(x_vals), lw=2, color='black', label='fit')
legend()
[ 5.12561007 1.01919966 0.99603507]
<matplotlib.legend.Legend at 0x1163135d0>
For other fitting, see scipy.optimize, in particular, curve_fit(). I have an exmaple gist here for exponetial fitting: https://gist.github.com/andrewgiessel/5816412, but the methodology can be used for any arbitrary function, using numpy routines and arrays.
6.5 Masked Arrays¶
There is a submodule of NumPy that can handle masked arrays- these are arrays with associated True/False values. These values are ignored during plotting or calcuations like mean(), max(), sum(), etc. If True, the value is masked.
A = np.random.random(100)
A_masked_small = np.ma.MaskedArray(A, A>0.5) # second arguement is the mask, must be the same shape as the array
A_masked_big = np.ma.MaskedArray(A, A<=0.5) # second arguement is the mask, must be the same shape as the array
print 'all average', A.mean()
print 'big average', A_masked_big.mean()
print 'small average', A_masked_small.mean()
figure(figsize=(12,8))
plot(A, label='full')
plot(A_masked_small, label='small')
plot(A_masked_big, label='big')
legend()
all average 0.52601171935 big average 0.763928864893 small average 0.246717678929
<matplotlib.legend.Legend at 0x116759910>
7. Other resources¶
There are a lot of great NumPy and scipy resources out there! I've gathered a few here.
- The NumPy Documentation: http://docs.scipy.org/doc/numpy/reference/
- NumPy For MATLAB Programmers: http://wiki.scipy.org/NumPy_for_Matlab_Users - a great reference if you come from MATLAB. Lots of similarities exist but there are some gotchas
- SciPy tutorial: http://docs.scipy.org/doc/scipy/reference/tutorial/ - NumPy users almost always end up using SciPy as well. Here is the intro docs for it.
- A youtube of a matplotlib/numpy tutorial session: http://www.youtube.com/watch?v=3Fp1zn5ao2M
- A great scientific python overview/tutorial site: http://scipy-lectures.github.io/