A tutorial on 'Soft weight-sharing for Neural Network compression'¶
Introduction¶
Recently, compression of neural networks has been a much-discussed issue. One reason for this is the desire to run and store them on mobile devices such as smartphones, robots or Rasberry Pis. Another problem is the energy consumption of a multimillion parameter network. When inference is run at scale the costs can quickly add up.
Compressing a given neural network is a challenging task. While the idea of storing weights with low precision has been around for some time, ideas to store the weight matrix in a different storage format are recent. The latter proposal has led to the most successful compression scheme so far. Under the assumption that there is great redundancy within the weights, one can prune most of them. Consequently, only non-zero weights are being stored. These weights can further be compressed by qunatizing them. However, it is not clear how to infer the redundant weights given a trained neural network or to quantize the remaining weights. In the following, we will identify the problem more clearly and review one recent attempt to tackle it. For the following illustrations, I work with MNIST and LeNet-300-100 a simple 2-fully connected neural network with 300 and 100 units.
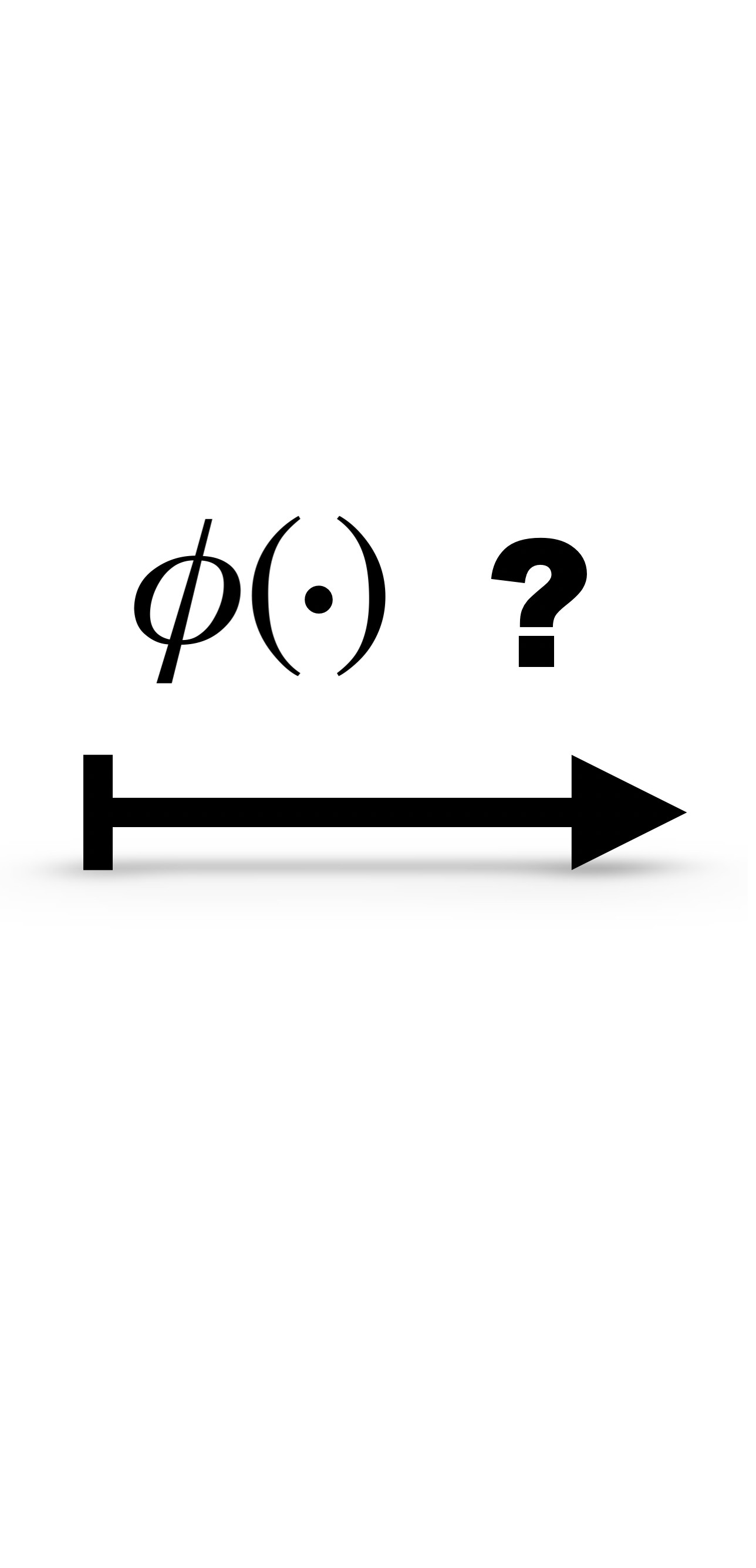
Usually, when training an unregularized neural network, the distribution of weights looks somewhat like a Normal distribution centered at zero. For the proposed storage format this is not ideal. We would like a distribution that is sharply (ideally delta) peaked around some values with significant mass in the zero peak.
| Weight distribution while common training | Desired distribution | |
|---|---|---|
 |
 |
 |
Following we will shortly review how Han et. al. (2016), the proposers of this compression format and current state-of-the-art in compression, tackle the problem. The authors use a multistage pipeline: (i) re-training a pre-trained network with Gaussian prior aka L2-norm on the weights (ii) repeatedly cutting off all weights around a threshold close to zero and after that continue training with L2-norm, and (iii) clustering all weights and retraining again the cluster means.
| (i) Re-training with L2 regularization | (ii) Repetitiv Cutting and training |
|---|---|
 |
 |
| (ii) Final stage before clustering | (iii) Clustering |
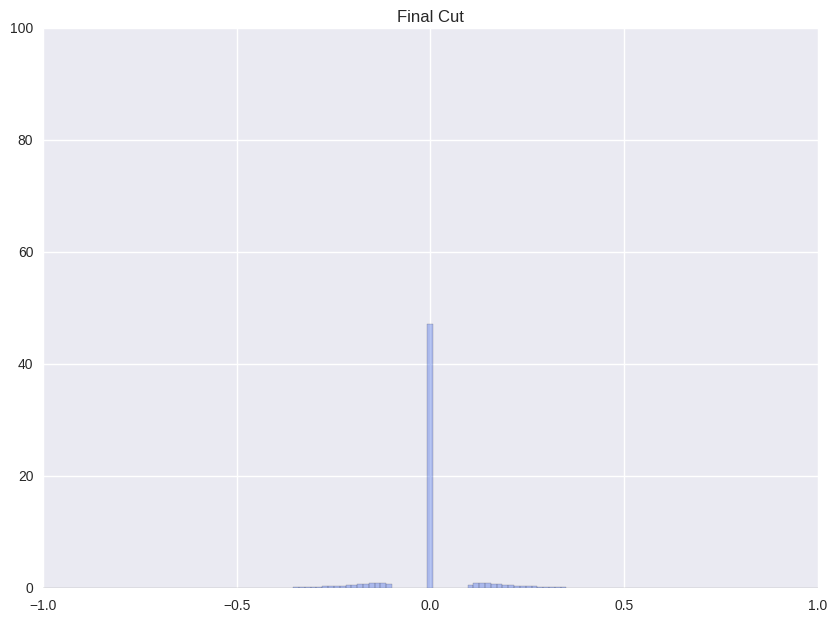 |
 |
Note that this pipeline is not a differentiable function. Furthermore, pruning and quantization are distinct stages.
In contrast, we propose to sparsify and cluster weights in one differentiable retraining procedure. More precisely, we train the network weights with a Gaussian mixture model prior. This is an instance of an empirical Bayesian prior because the parameters in the prior are being learned as well. With this prior present, weights will naturally cluster together since that will allow the gaussian mixture to lower the variance and thus achieve higher probability. It is important, to carefully initialize the learning procedure for those priors because one might end up in a situation where the weights "chase" the mixture and the mixture the weights.
Note that, even though compression seems to be a core topic of information theory, so far there has been little attention on this angle on things. While in our paper the emphasis lays on this information theoretic view, here we will restrict ourselves to a somewhat practical one.
Following, we give a tutorial that shall serve as a practical guide to implementing empirical priors and in particular a Gaussian Mixture with an Inverse-Gamma prior on the variances. It is divided into 3 parts.
PART 1: Pretraining a Neural Network
PART 2: Re-train the network with an empirical Gaussian Mixture Prior with Inverse-Gamma hyper-prior on the variances.
PART 3: Post-process the re-trained network weights
PART 1: Pretraining a Neural Network¶
First of all, we need a parameter heavy network to compress. In this first part of the tutorial, we train a simple -2 convolutional, 2 fully connected layer- neural network on MNIST with 642K paramters. ___________________________
We start by loading some essential libraries.
from __future__ import print_function
import numpy as np
%matplotlib inline
import keras
from IPython import display
Using Theano backend. Using gpu device 0: GeForce GTX TITAN X (CNMeM is enabled with initial size: 70.0% of memory, cuDNN 5103) /home/karen/anaconda2/lib/python2.7/site-packages/theano/sandbox/cuda/__init__.py:600: UserWarning: Your cuDNN version is more recent than the one Theano officially supports. If you see any problems, try updating Theano or downgrading cuDNN to version 5. warnings.warn(warn)
Following, we load the MNIST dataset into memory.
from dataset import mnist
[X_train, X_test], [Y_train, Y_test], [img_rows, img_cols], nb_classes = mnist()
Successfully loaded 60000 train samples and 10000 test samples.
Next, we choose a model. We decide in favor of a classical 2 convolutional, 2 fully connected layer network with ReLu activation.
from keras import backend as K
from keras.models import Model
from keras.layers import Input, Dense, Activation, Flatten, Convolution2D
# We configure the input here to match the backend. If properly done this is a lot faster.
if K._BACKEND == "theano":
InputLayer = Input(shape=(1, img_rows, img_cols), name="input")
elif K._BACKEND == "tensorflow":
InputLayer = Input(shape=(img_rows, img_cols,1), name="input")
# A classical architecture ...
# ... with 3 convolutional layers,
Layers = Convolution2D(25, 5, 5, subsample = (2,2), activation = "relu")(InputLayer)
Layers = Convolution2D(50, 3, 3, subsample = (2,2), activation = "relu")(Layers)
# ... and 2 fully connected layers.
Layers = Flatten()(Layers)
Layers = Dense(500)(Layers)
Layers = Activation("relu")(Layers)
Layers = Dense(nb_classes)(Layers)
PredictionLayer = Activation("softmax", name ="error_loss")(Layers)
# Fianlly, we create a model object:
model = Model(input=[InputLayer], output=[PredictionLayer])
model.summary()
____________________________________________________________________________________________________ Layer (type) Output Shape Param # Connected to ==================================================================================================== input (InputLayer) (None, 1, 28, 28) 0 ____________________________________________________________________________________________________ convolution2d_1 (Convolution2D) (None, 25, 12, 12) 650 input[0][0] ____________________________________________________________________________________________________ convolution2d_2 (Convolution2D) (None, 50, 5, 5) 11300 convolution2d_1[0][0] ____________________________________________________________________________________________________ flatten_1 (Flatten) (None, 1250) 0 convolution2d_2[0][0] ____________________________________________________________________________________________________ dense_1 (Dense) (None, 500) 625500 flatten_1[0][0] ____________________________________________________________________________________________________ activation_1 (Activation) (None, 500) 0 dense_1[0][0] ____________________________________________________________________________________________________ dense_2 (Dense) (None, 10) 5010 activation_1[0][0] ____________________________________________________________________________________________________ error_loss (Activation) (None, 10) 0 dense_2[0][0] ==================================================================================================== Total params: 642,460 Trainable params: 642,460 Non-trainable params: 0 ____________________________________________________________________________________________________
Next, we train the network for 100 epochs with the Adam optimizer. Let's see where our model gets us...
from keras import optimizers
epochs = 100
batch_size = 256
opt = optimizers.Adam(lr=0.001)
model.compile(optimizer= opt,
loss = {"error_loss": "categorical_crossentropy",},
metrics=["accuracy"])
model.fit({"input": X_train, }, {"error_loss": Y_train},
nb_epoch = epochs, batch_size = batch_size,
verbose = 0, validation_data=(X_test, Y_test))
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test accuracy:', score[1])
Test accuracy: 0.9908
*Note: * The model should end up with approx. 0.9% error rate. ___________________________________ Fianlly, we save the model in case we need to reload it later, e.g. if you want to play around with the code ...
keras.models.save_model(model, "./my_pretrained_net")
pretrained_model = keras.models.load_model("./my_pretrained_net")
Following, we will initialize a 16 component Gaussian mixture as our empirical prior. We will learn all parameters in the prior but the mean and the mixing proportion of the zero component, we set $\mu_0=0$ and $\pi_0=0.99$, respectively. Furthermore, we put a Gamma hyper-prior on the precisions of the Gaussian mixture. We set the mean such that the expected variance is $0.02$. The variance of the hyper-prior is an estimate of how strongly the variance is regularized. Note that, the variance of the zero component has much more data (i.e. weight) evidence than the other components thus we put a stronger prior on it. Somewhat counterintuitive we found it beneficial to have wider and thus noisier expected variances.
from empirical_priors import GaussianMixturePrior
from extended_keras import extract_weights
pi_zero = 0.99
RegularizationLayer = GaussianMixturePrior(nb_components=16,
network_weights=extract_weights(model),
pretrained_weights=pretrained_model.get_weights(),
pi_zero=pi_zero,
name="complexity_loss")(Layers)
model = Model(input = [InputLayer], output = [PredictionLayer, RegularizationLayer])
We optimize the network again with ADAM, the learning rates for the network parameters, means, variances and mixing proportions may differ though.
import optimizers
from extended_keras import identity_objective
tau = 0.003
N = X_train.shape[0]
opt = optimizers.Adam(lr = [5e-4,1e-4,3e-3,3e-3], #[unnamed, means, log(precition), log(mixing proportions)]
param_types_dict = ['means','gammas','rhos'])
model.compile(optimizer = opt,
loss = {"error_loss": "categorical_crossentropy", "complexity_loss": identity_objective},
loss_weights = {"error_loss": 1. , "complexity_loss": tau/N},
metrics = ['accuracy'])
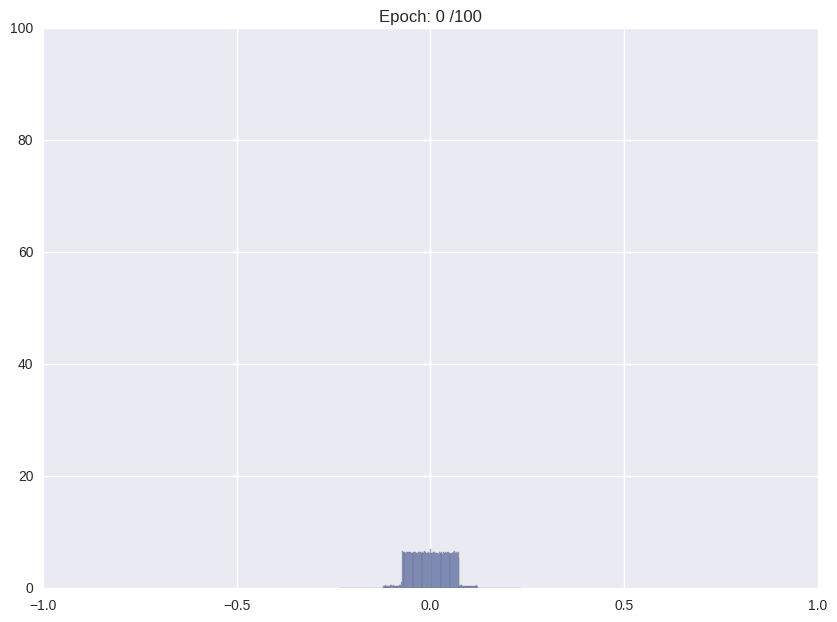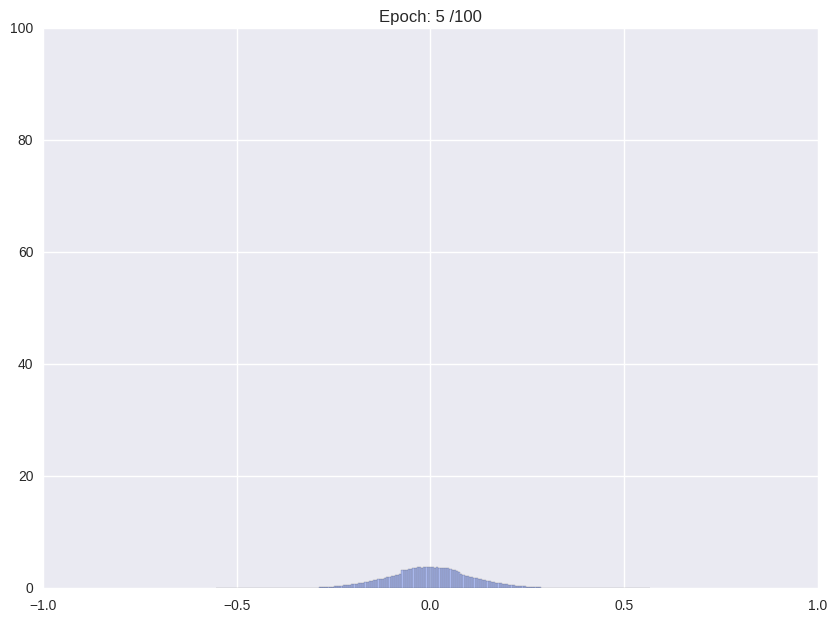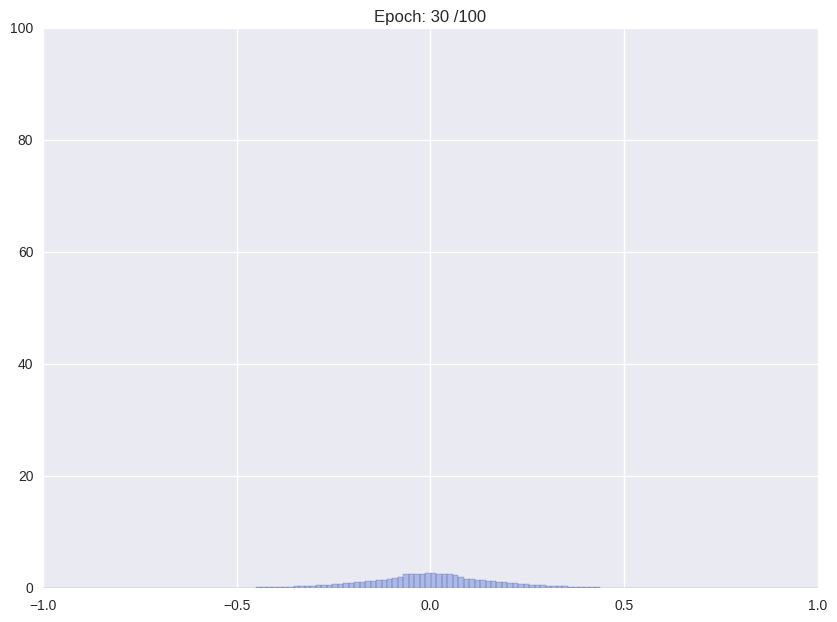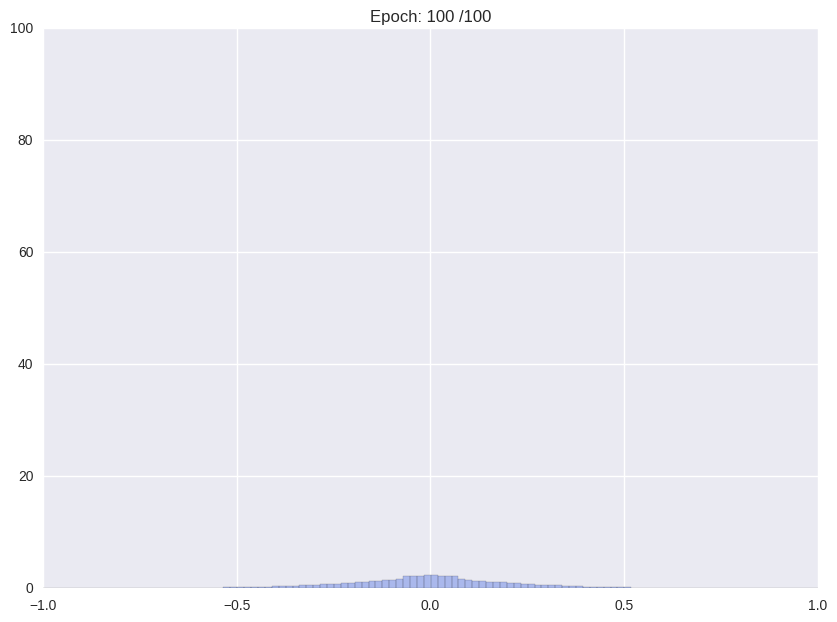
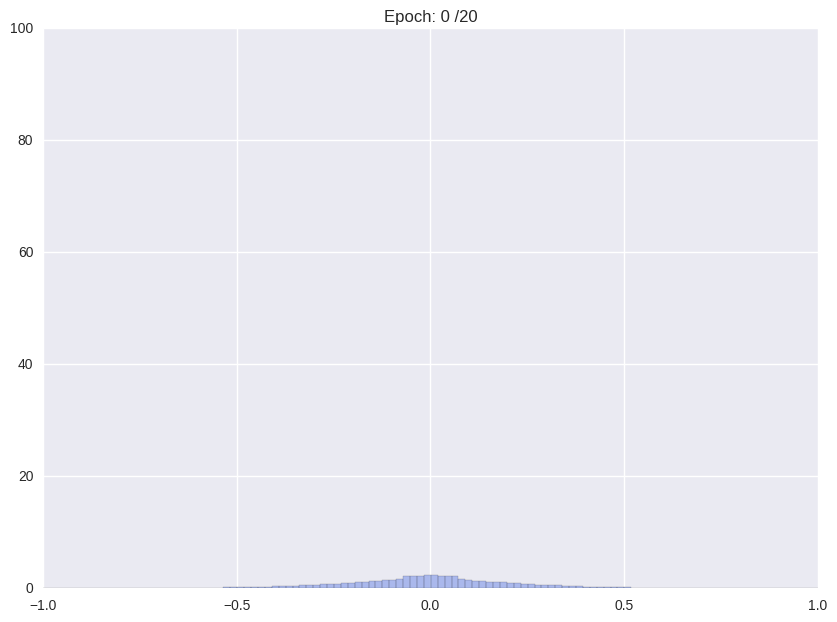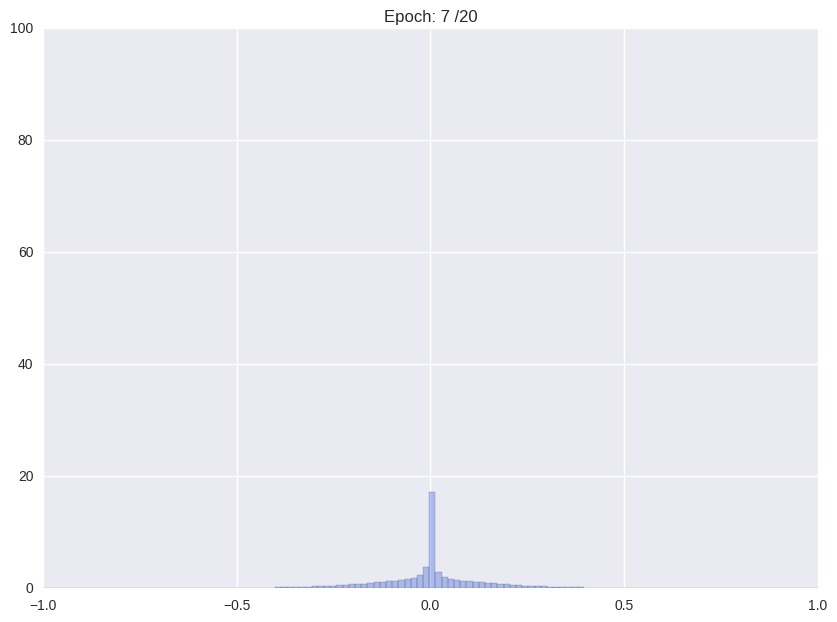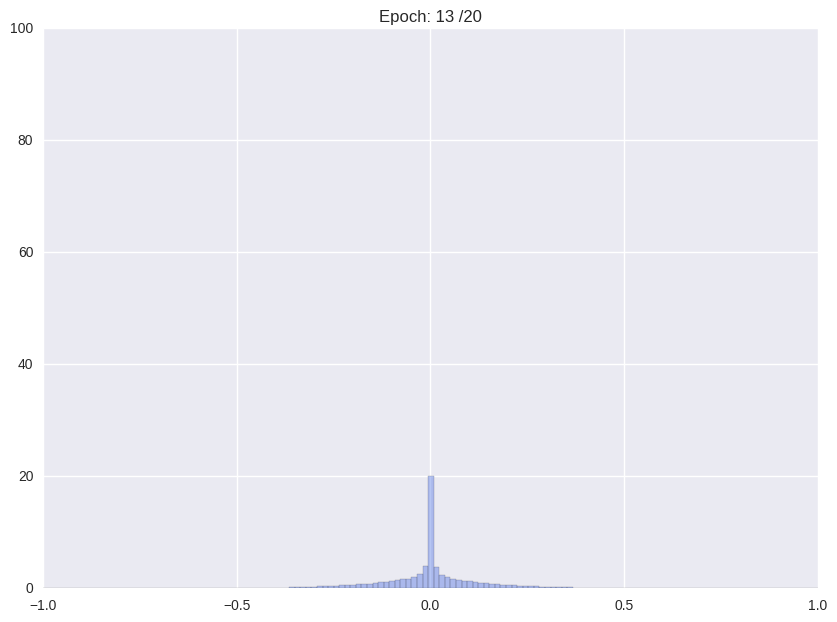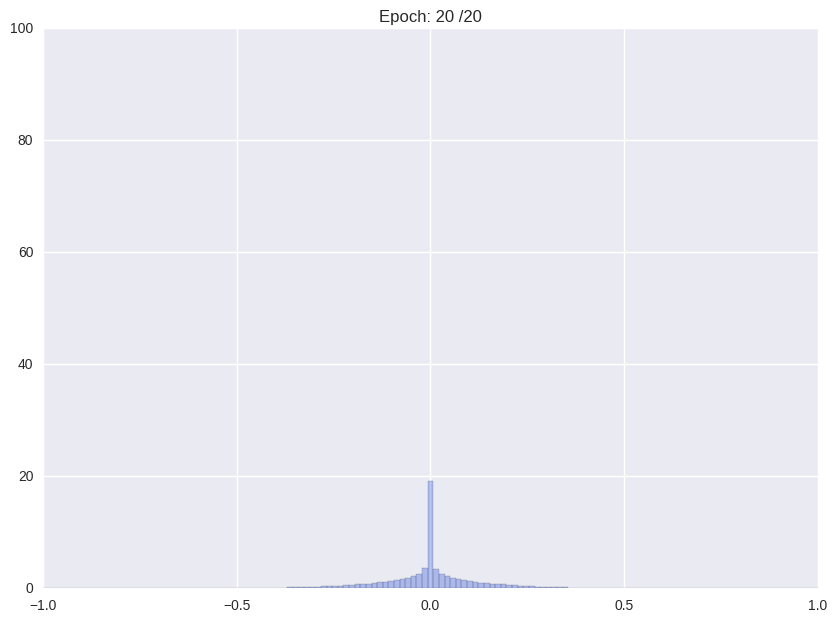
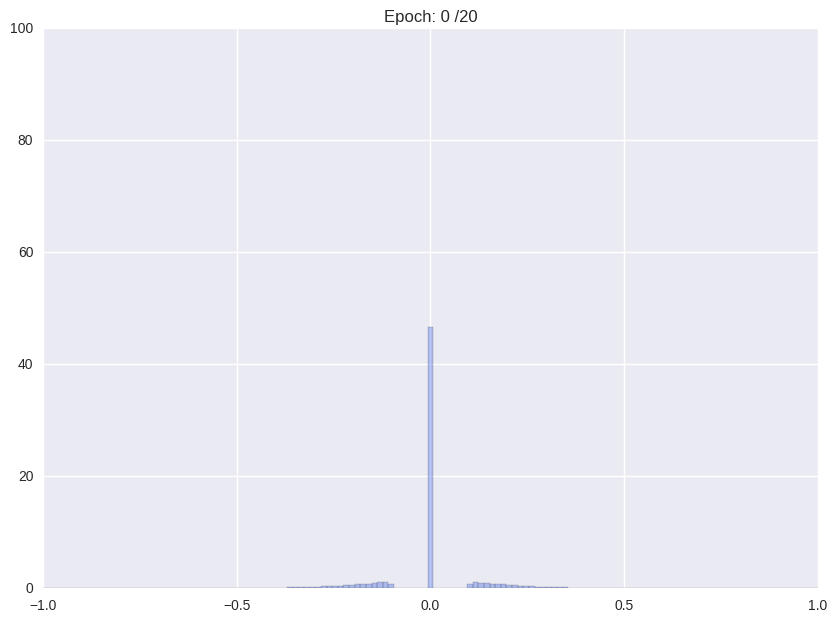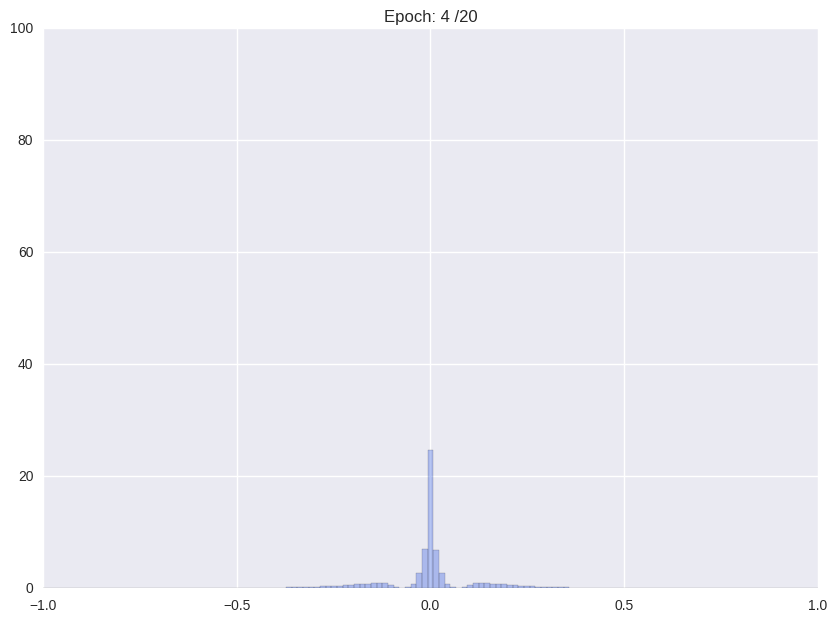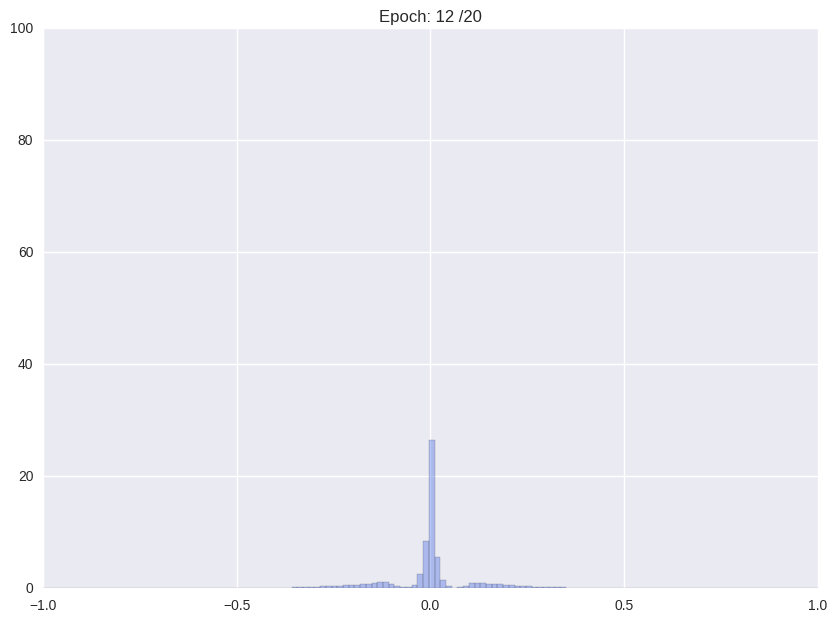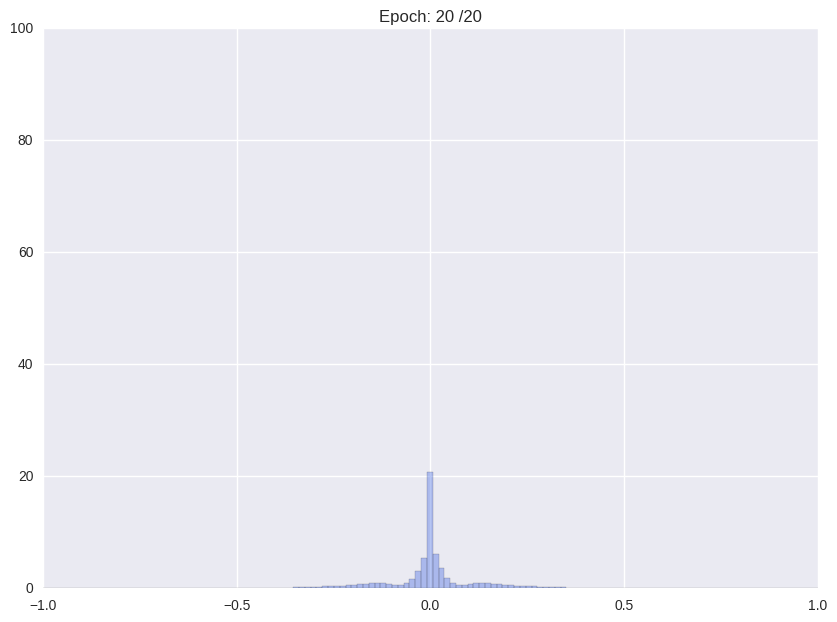
We train our network for 30 epochs, each taking about 45s. You can watch the progress yourself. At each epoch, we compare the original weight distribution (histogram top) to the current distribution (log-scaled histogram right). The joint scatter plot in the middle shows how each weight changed.
Note that we had to scale the histogram logarithmically otherwise it would be little informative due to the zero spike.
from extended_keras import VisualisationCallback
epochs = 30
model.fit({"input": X_train,},
{"error_loss" : Y_train, "complexity_loss": np.zeros((N,1))},
nb_epoch = epochs,
batch_size = batch_size,
verbose = 1., callbacks=[VisualisationCallback(model,X_test,Y_test, epochs)])
display.clear_output()
display.Image(url='./figures/retraining.gif')
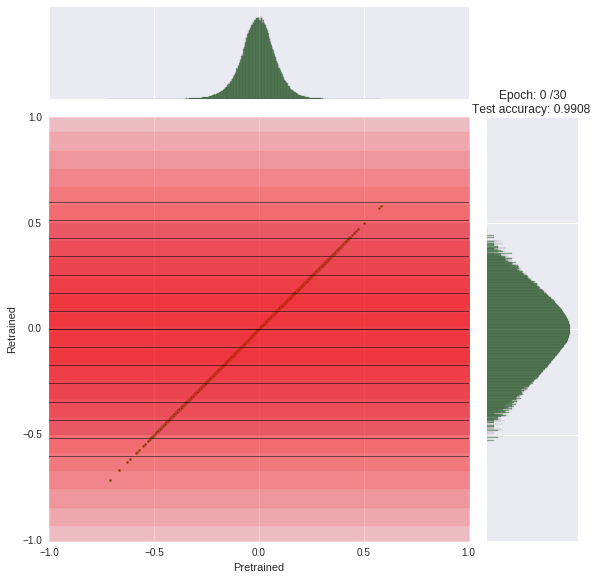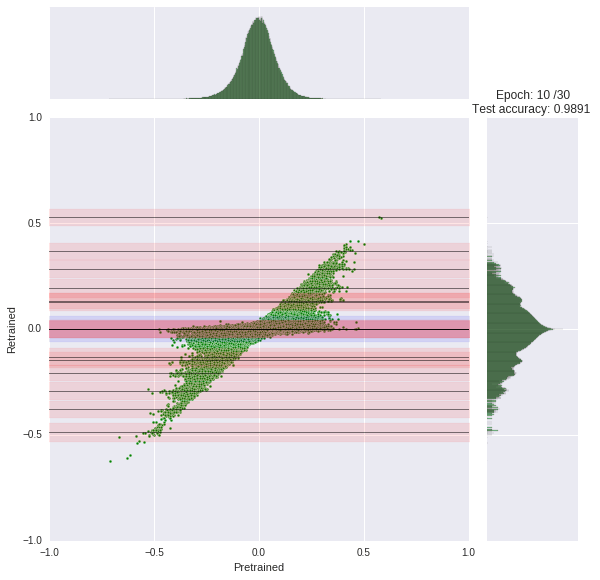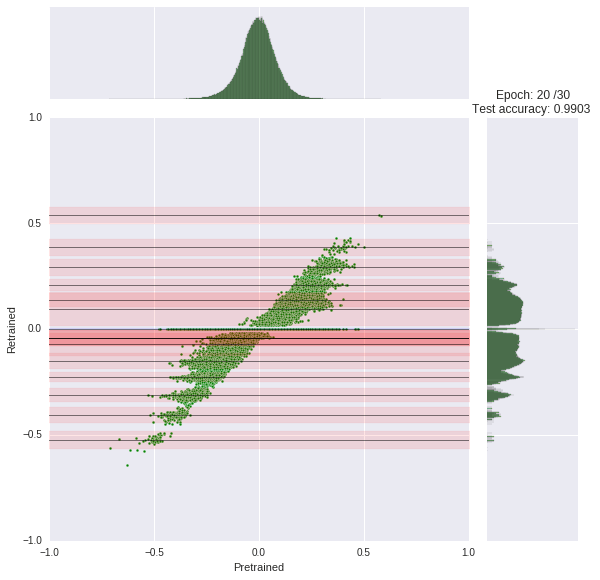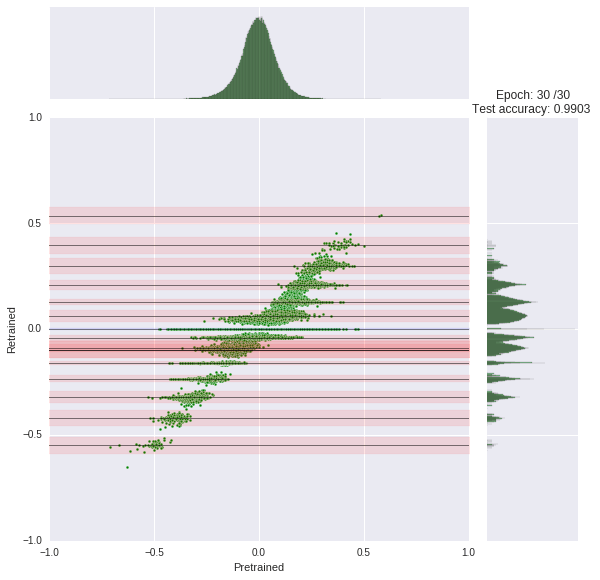
PART 3: Post-processing¶
Now, the only thing that is left to do is setting each weight to the mean of the component that takes most responsibility for it i.e. quantising the weights.
from helpers import discretesize
retrained_weights = np.copy(model.get_weights())
compressed_weights = np.copy(model.get_weights())
compressed_weights[:-3] = discretesize(compressed_weights, pi_zero = pi_zero)
Let us compare the accuracy of the reference, the retrained and the post-processed network.
print("MODEL ACCURACY")
score = pretrained_model.evaluate({'input': X_test, },{"error_loss" : Y_test,}, verbose=0)[1]
print("Reference Network: %0.4f" %score)
score = model.evaluate({'input': X_test, },{"error_loss" : Y_test, "complexity_loss": Y_test,}, verbose=0)[3]
print("Retrained Network: %0.4f" %score)
model.set_weights(compressed_weights)
score = model.evaluate({'input': X_test, },{"error_loss" : Y_test, "complexity_loss": Y_test,}, verbose=0)[3]
print("Post-processed Network: %0.4f" %score)
MODEL ACCURACY Reference Network: 0.9908 Retrained Network: 0.9903 Post-processed Network: 0.9902
Finally let us see how many weights have been pruned.
from helpers import special_flatten
weights = special_flatten(compressed_weights[:-3]).flatten()
print("Non-zero weights: %0.2f %%" % (100.*np.count_nonzero(weights)/ weights.size) )
Non-zero weights: 7.43 %
As we can see in this naive implementation we got rid of 19 out of 20 weights. Furthermore note that we quantize weights with only 16 cluster means (aka 4 bit indexes).
For better results (up to 0.5%) one may anneal $\tau$, learn the mixing proportion for the zero spike with a beta prior on it for example and ideally optimize with some hyperparamter optimization of choice such as spearmint (I also wrote some example code for deep learning and spearmint).
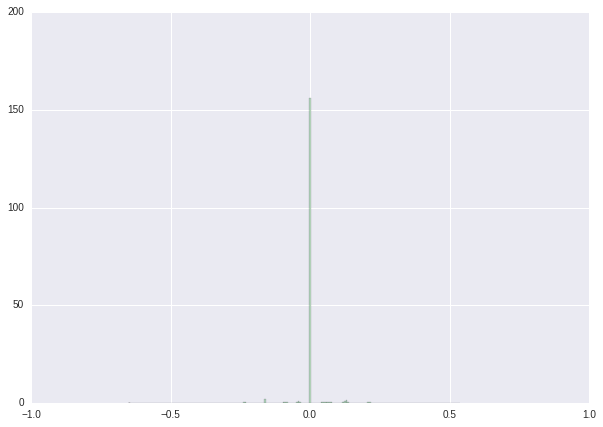
We finish this tutorial with a series of histograms showing the results of our procedure.
from helpers import save_histogram
save_histogram(pretrained_model.get_weights(),save="figures/reference")
save_histogram(retrained_weights,save="figures/retrained")
save_histogram(compressed_weights,save="figures/post-processed")
| Weight distribution before retraining | Weight distribution after retraining | Weight distribution after post-processing | |
|---|---|---|---|
| histogram | 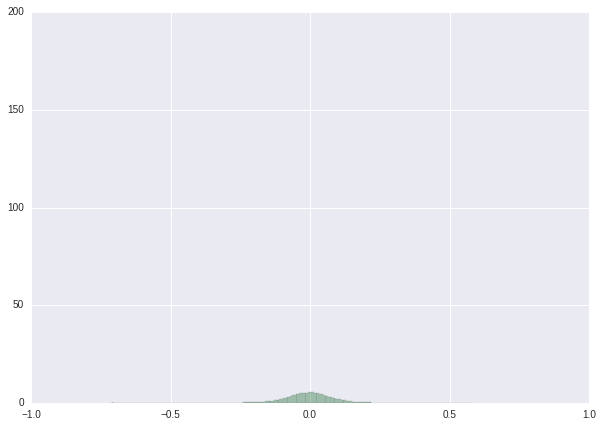 |
 |
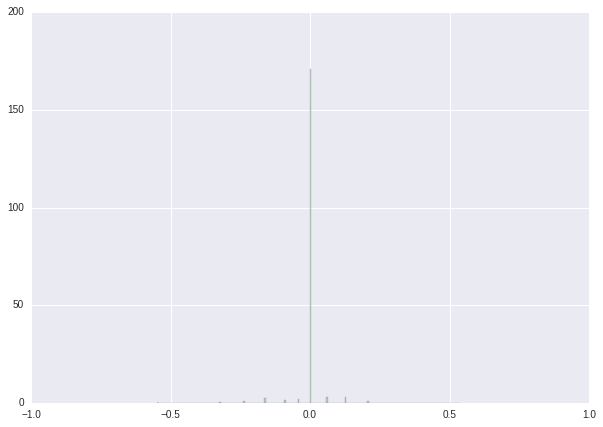 |
| log-scaled histogram |  |
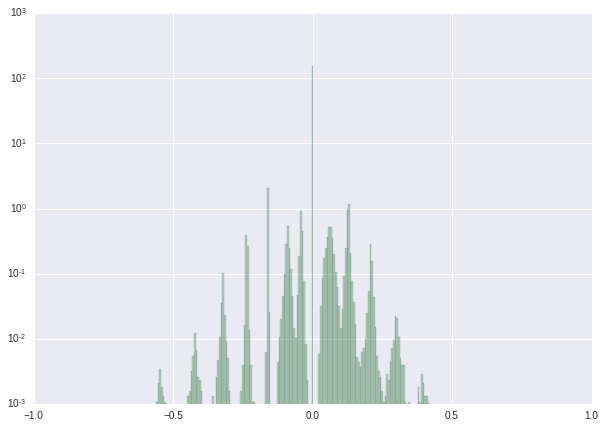 |
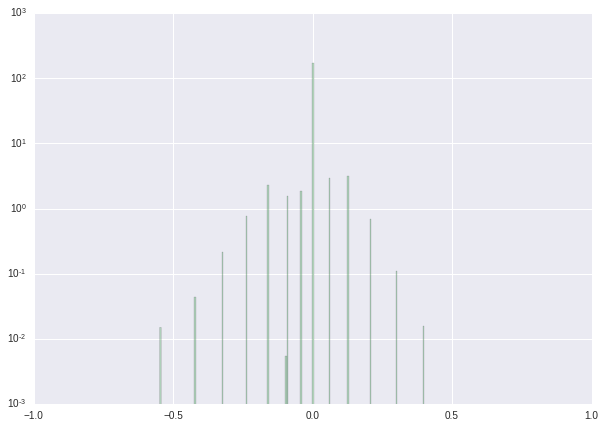 |
Reference¶
The paper "Soft weight-sharing for Neural Network compression" has been accepted to ICLR 2017.
@inproceedings{ullrich2017soft,
title={Soft Weight-Sharing for Neural Network Compression},
author={Ullrich, Karen and Meeds, Edward and Welling, Max},
booktitle={ICLR 2017},
year={2017}
}