Python for Everyone!
Oregon Curriculum Network
Polyhedrons¶
Polyhedrons make a great entry point into mathematics, because they're not only pretty to look at, they're graphs (as in Graph Theory), a kind of data structure, made of nodes and edges.
The edges border openings we call "faces" though in wireframe polys, these may be more like "windows", not filled in.
Consider: in modern data analysis and machine learning, we stack up the vectors, or features, in our X rectangle, corresponding to y labels. A vector is both a geometric object and a pointer to anywhere in an n-dimensional phase space.
Because n-dimensional polytopes and data analysis go together, it makes sense to introduce them in tandem, with Polyhedrons in relational data tables.
Here in Oregon, we have a predeliction to introduce a scheme of nested polyhedrons of more whole number volumes than you may be expecting. We make use of the so-called Concentric Hierarchy based around a central Tetrahedron of unit volume. Other volumes get measured in tetravolumes.
Consider this table:
|
Shape
|
Volume
|
Scale
|
| Tetrahedron |
1.0000
|
1.0000
|
| Cuboctahedron |
2.5000
|
0.5000
|
| Icosahedron 1 |
~2.9180
|
~0.5402
|
| Duo-Tet Cube |
3.0000
|
1.0000
|
| Octahedron |
4.0000
|
1.0000
|
| Rhombic Triacontahedron |
5.0000
|
~0.9995
|
| Rhombic Triacontahedron 2 |
~5.0078
|
1.0000
|
| Pentagonal Dodecahedron 3 |
5.4271
|
~0.7071
|
| Rhombic Dodecahedron 4 |
6.0000
|
1.0000
|
| Pentagonal Dodecahedron 5 |
~15.3500
|
1.0000
|
| Icosahedron |
~18.5123
|
1.0000
|
| Cuboctahedron |
20.0000
|
1.0000
|
| Duo-Tet Cube |
24.0000
|
2.0000
|
|
1 faces flush with
volume 4 octahedron's |
||
Now lets take a look at what these look like, minus a few to keep the picture uncluttered:
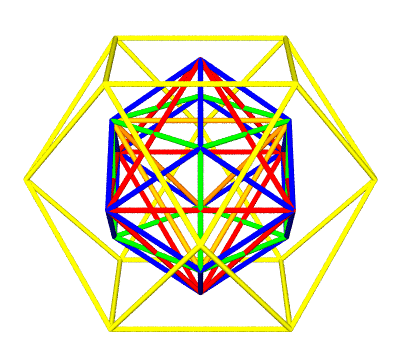
We can pull up the coordinates for these polyhedrons from an SQL database. Polyhedrons give us an entry point into databases as well. We could use a Graph Database, such as Neo4j, but lets stick with a language called SQL.
import sqlite3 as sql
import os
from pprint import pprint
class DB:
backend = 'sqlite3' # default
target_path = os.getcwd() # current directory
db_name = ":file:" # lets work directly with a file
db_name = os.path.join(target_path, 'shapes_lib.db')
@classmethod
def connect(cls):
if cls.backend == 'sqlite3':
DB.conn = sql.connect(DB.db_name)
DB.c = DB.conn.cursor()
elif cls.backend == 'postgres': # or something else
DB.conn = sql.connect(host='localhost',
user='root', port='8889')
DB.c = DB.conn.cursor()
return DB
__enter__ = connect # allows optional syntax to trigger
@classmethod
def disconnect(cls):
DB.conn.close()
def __exit__(cls, *oops): # in case of context manager syntax
cls.disconnect()
if oops[0]:
return False
return True
The DB class contains information for connecting to a SQLite database, which may be accessed directly, as a text file, no need for a special server. SQLite is free of charge.
The database was created earlier.
with DB() as db:
db.c.execute("SELECT poly_long, poly_color, poly_volume from Polys") # query
pprint(db.c.fetchall()) # print results
[('Tetrahedron', 'Orange', 1.0),
('Inverse Tetrahedron', 'Black', 1.0),
('Cube', 'Green', 3.0),
('Octahedron', 'Red', 4.0),
('Rhombic Dodecahedron', 'Blue', 6.0),
('Cuboctahedron', 'Yellow', 20.0)]
What we see above is connecting to the database, running a one-liner, a SELECT query, and pretty-printing the results. Then disconnecting.
These volumes are whole numbers. Lets look at their coordinates.
with DB() as db:
db.c.execute("SELECT vertex_label, coord_a, coord_b, coord_c, coord_d FROM Coords ORDER BY vertex_label") # query
pprint(db.c.fetchall()) # print results
[('A', 1.0, 0.0, 0.0, 0.0),
('B', 0.0, 1.0, 0.0, 0.0),
('C', 0.0, 0.0, 1.0, 0.0),
('D', 0.0, 0.0, 0.0, 1.0),
('E', 0.0, 1.0, 1.0, 1.0),
('F', 1.0, 0.0, 1.0, 1.0),
('G', 1.0, 1.0, 0.0, 1.0),
('H', 1.0, 1.0, 1.0, 0.0),
('I', 1.0, 1.0, 0.0, 0.0),
('J', 1.0, 0.0, 1.0, 0.0),
('K', 1.0, 0.0, 0.0, 1.0),
('L', 0.0, 1.0, 1.0, 0.0),
('M', 0.0, 1.0, 0.0, 1.0),
('N', 0.0, 0.0, 1.0, 1.0),
('O', 2.0, 1.0, 1.0, 0.0),
('P', 2.0, 1.0, 0.0, 1.0),
('Q', 1.0, 2.0, 1.0, 0.0),
('R', 1.0, 2.0, 0.0, 1.0),
('S', 1.0, 0.0, 2.0, 1.0),
('T', 1.0, 0.0, 1.0, 2.0),
('U', 0.0, 1.0, 2.0, 1.0),
('V', 0.0, 1.0, 1.0, 2.0),
('W', 1.0, 1.0, 2.0, 0.0),
('X', 0.0, 2.0, 1.0, 1.0),
('Y', 1.0, 1.0, 0.0, 2.0),
('Z', 2.0, 0.0, 1.0, 1.0)]
Why are these coordinates integers and why are there four of them per labeled vertex? Is this another "legal in Oregon" thing?
These are Quadray Coordinates, which you may read more about on Wikipedia.
Here's a diagram giving a sense of what letters go with what shapes:

Converting to XYZ is pretty easy, especially with a computer.
Lets see those 26 vertexes in XYZ coordinates instead:
with DB() as db:
db.c.execute("SELECT vertex_label, coord_x, coord_y, coord_z FROM Coords ORDER BY vertex_label") # query
pprint(db.c.fetchall()) # print results
[('A', 0.35355339059327373, 0.35355339059327373, 0.35355339059327373),
('B', -0.35355339059327373, -0.35355339059327373, 0.35355339059327373),
('C', -0.35355339059327373, 0.35355339059327373, -0.35355339059327373),
('D', 0.35355339059327373, -0.35355339059327373, -0.35355339059327373),
('E', -0.35355339059327373, -0.35355339059327373, -0.35355339059327373),
('F', 0.35355339059327373, 0.35355339059327373, -0.35355339059327373),
('G', 0.35355339059327373, -0.35355339059327373, 0.35355339059327373),
('H', -0.35355339059327373, 0.35355339059327373, 0.35355339059327373),
('I', 0.0, 0.0, 0.7071067811865475),
('J', 0.0, 0.7071067811865475, 0.0),
('K', 0.7071067811865475, 0.0, 0.0),
('L', -0.7071067811865475, 0.0, 0.0),
('M', 0.0, -0.7071067811865475, 0.0),
('N', 0.0, 0.0, -0.7071067811865475),
('O', 0.0, 0.7071067811865475, 0.7071067811865475),
('P', 0.7071067811865475, 0.0, 0.7071067811865475),
('Q', -0.7071067811865475, 0.0, 0.7071067811865475),
('R', 0.0, -0.7071067811865475, 0.7071067811865475),
('S', 0.0, 0.7071067811865475, -0.7071067811865475),
('T', 0.7071067811865475, 0.0, -0.7071067811865475),
('U', -0.7071067811865475, 0.0, -0.7071067811865475),
('V', 0.0, -0.7071067811865475, -0.7071067811865475),
('W', -0.7071067811865475, 0.7071067811865475, 0.0),
('X', -0.7071067811865475, -0.7071067811865475, 0.0),
('Y', 0.7071067811865475, -0.7071067811865475, 0.0),
('Z', 0.7071067811865475, 0.7071067811865475, 0.0)]
As shown below, we're not obligated to use the DB class as a context manager, in which case we may call the class's methods directly. Context manager syntax is a little cleaner and more likely to disconnect in case of issues.
DB.connect()
DB.c.execute("SELECT * FROM Coords ORDER BY vertex_label") # query
for rec in DB.c.fetchall():
print(rec) # print results
DB.disconnect()
('A', 1.0, 0.0, 0.0, 0.0, 0.35355339059327373, 0.35355339059327373, 0.35355339059327373, None)
('B', 0.0, 1.0, 0.0, 0.0, -0.35355339059327373, -0.35355339059327373, 0.35355339059327373, None)
('C', 0.0, 0.0, 1.0, 0.0, -0.35355339059327373, 0.35355339059327373, -0.35355339059327373, None)
('D', 0.0, 0.0, 0.0, 1.0, 0.35355339059327373, -0.35355339059327373, -0.35355339059327373, None)
('E', 0.0, 1.0, 1.0, 1.0, -0.35355339059327373, -0.35355339059327373, -0.35355339059327373, None)
('F', 1.0, 0.0, 1.0, 1.0, 0.35355339059327373, 0.35355339059327373, -0.35355339059327373, None)
('G', 1.0, 1.0, 0.0, 1.0, 0.35355339059327373, -0.35355339059327373, 0.35355339059327373, None)
('H', 1.0, 1.0, 1.0, 0.0, -0.35355339059327373, 0.35355339059327373, 0.35355339059327373, None)
('I', 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.7071067811865475, None)
('J', 1.0, 0.0, 1.0, 0.0, 0.0, 0.7071067811865475, 0.0, None)
('K', 1.0, 0.0, 0.0, 1.0, 0.7071067811865475, 0.0, 0.0, None)
('L', 0.0, 1.0, 1.0, 0.0, -0.7071067811865475, 0.0, 0.0, None)
('M', 0.0, 1.0, 0.0, 1.0, 0.0, -0.7071067811865475, 0.0, None)
('N', 0.0, 0.0, 1.0, 1.0, 0.0, 0.0, -0.7071067811865475, None)
('O', 2.0, 1.0, 1.0, 0.0, 0.0, 0.7071067811865475, 0.7071067811865475, None)
('P', 2.0, 1.0, 0.0, 1.0, 0.7071067811865475, 0.0, 0.7071067811865475, None)
('Q', 1.0, 2.0, 1.0, 0.0, -0.7071067811865475, 0.0, 0.7071067811865475, None)
('R', 1.0, 2.0, 0.0, 1.0, 0.0, -0.7071067811865475, 0.7071067811865475, None)
('S', 1.0, 0.0, 2.0, 1.0, 0.0, 0.7071067811865475, -0.7071067811865475, None)
('T', 1.0, 0.0, 1.0, 2.0, 0.7071067811865475, 0.0, -0.7071067811865475, None)
('U', 0.0, 1.0, 2.0, 1.0, -0.7071067811865475, 0.0, -0.7071067811865475, None)
('V', 0.0, 1.0, 1.0, 2.0, 0.0, -0.7071067811865475, -0.7071067811865475, None)
('W', 1.0, 1.0, 2.0, 0.0, -0.7071067811865475, 0.7071067811865475, 0.0, None)
('X', 0.0, 2.0, 1.0, 1.0, -0.7071067811865475, -0.7071067811865475, 0.0, None)
('Y', 1.0, 1.0, 0.0, 2.0, 0.7071067811865475, -0.7071067811865475, 0.0, None)
('Z', 2.0, 0.0, 1.0, 1.0, 0.7071067811865475, 0.7071067811865475, 0.0, None)
The database in question consists of three tables: Polys, Faces, and Coords. A polyhedron is defined in terms of its faces, such as ('A', 'B', 'C') which would consist of the three edges connecting 'A' to 'B', 'B' to 'C' and 'C' back to 'A'. From faces, a computer deduces edges. Edges terminate in labeled points, for which the database stores coordinates.
Lets remember the INNER JOIN semantics. Those go with LEFT JOIN and OUTER JOIN, with not every SQL engine making the same promises. Getting a query right takes trial and error. One often goes up against dummy data during testing and development. Then might come staging, wherein the workload is tested to production levels before release.
There query below filters on one row of the Polys table, that of the rhombic dodecahedron (RD), and then starts in the Faces, pulling up matching in nickname, meaning RD on both sides.
The intersection is a set of twelve rows, each a face of the diamond-faced dodecahedron. Every face is a tuple of four vertexes, labels paired with their coordinates in the Coords table.
query3 = ("""
SELECT f.poly_nick, f.poly_face_id, f.vertex_labels, p.poly_long
FROM Polys p
INNER JOIN Faces f ON f.poly_nick = p.poly_nick
WHERE p.poly_nick = "RD"
""")
with DB() as db:
db.c.execute(query3) # query
pprint(db.c.fetchall()) # print results
[('RD', 22, '("J", "F", "K", "A")', 'Rhombic Dodecahedron'),
('RD', 23, '("J", "F", "N", "C")', 'Rhombic Dodecahedron'),
('RD', 24, '("J", "C", "L", "H")', 'Rhombic Dodecahedron'),
('RD', 25, '("J", "H", "I", "A")', 'Rhombic Dodecahedron'),
('RD', 26, '("M", "D", "K", "G")', 'Rhombic Dodecahedron'),
('RD', 27, '("M", "D", "N", "E")', 'Rhombic Dodecahedron'),
('RD', 28, '("M", "E", "L", "B")', 'Rhombic Dodecahedron'),
('RD', 29, '("M", "B", "I", "G")', 'Rhombic Dodecahedron'),
('RD', 30, '("K", "D", "N", "F")', 'Rhombic Dodecahedron'),
('RD', 31, '("N", "C", "L", "E")', 'Rhombic Dodecahedron'),
('RD', 32, '("L", "H", "I", "B")', 'Rhombic Dodecahedron'),
('RD', 33, '("I", "A", "K", "G")', 'Rhombic Dodecahedron')]
In Conclusion¶
The key idea here is Geometry meets Data Science via the N-dimensional vector, which where N=1,2,3 is familiar Cartesian space. Sure, I still use the Weird and Twisted (to some it seems), lets say for contrast. The conventional seems all the more so once you've realized a true alternative.
My impression is IB math (EU curriculum) is more likely to feature 3D vectors with rotation matrices i.e. stays geometric longer.
A lot of school systems in the Americas go for that "geometry sandwich" with two slices of Algebra for bread. Dr. David DiNucci (NASA computer science) showed me an article about that.
The meat (10th grade geometry it's often called) is very thin, in the sense of planar. Mr. Euclid is milked for his proof of the proof concept, and meanwhile we're not "wasting time" with 3D printing or CAD renderings.
A lot of people are getting nervous about Shop and real tool use. Weren't schools supposed to teach about trades too? That's where a more hands-on geometry (e.g. this one) with SQL practice, in storing and retrieving the vectors, face topology, might help.
Milo Gardner (curriculum historian) suggests the big chunk of Euclid traces to political agendas to suppress all things German. Gauss and Number Theory needed less airtime. However along this same "lambda calc" track that'd feature SQL and real tool use, we'd put more about crypto. Number Theory is back on the front burner, along with Fermat's Little Theorem and Carmichael Numbers.