Notes on Neural Networks and Deep Learning, chapter 1¶
This notebook collects notes and code from Chapter 1 of Neural Networks and Deep Learning, chapter 1.
Foundations: Perceptron¶
A perceptron simply takes a weighted combination of its inputs and outputs a binary $1$ or $0$ when this combination is larger than some threshold: $$ \mathrm{output} = \begin{cases} 1 & Wx + b \le 0\\ 0 & Wx + b > 0\end{cases} $$ where $x \in \mathbb{R}^n$ is a feature vector describing some data, $W \in \mathbb{R}^{1 \times n}$ is a mixing (row) vector which denotes the weight of each feature dimension, and $b \in \mathbb{R}$ is the threshold value or bias. Intuitively, $W$ controls how "important" each value of $x$ is, and $b$ decides at which point the true/false decision should be made.
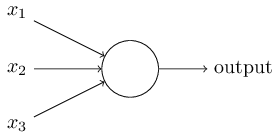
The Neural Network¶
A straightforward extension of the perceptron is to create a network of layers of perceptrons (or units), where units from one layer are connected to units in the next:
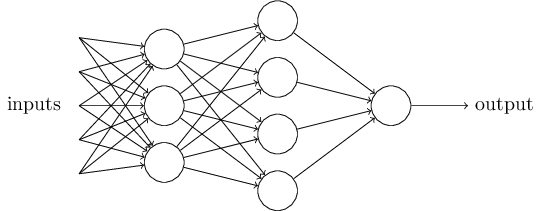
In this setting, the mixing weights for each layer become a matrix $W \in \mathbb{R}^{m \times n}$ and the threshold (or bias) becomes a vector $b \in \mathbb{R}^m$, where $n$ is the number of inputs to a layer and $m$ is the number of outputs.
One additional deviation from the original perceptron is that in practice we typically use a logistic function instead of a hard threshold. That is, instead of switching immediately between $0$ and $1$, we use a function which transitions between the two values smoothly. This is so that a small change in the $W$ or $b$ doesn't cause a large change in the output when $Wx + b$ is close to $0$, or in other words, so that the network function is differentiable. A common choise is the logistic sigmoid: $$ \sigma(z) = \frac{1}{1 + e^{-z}} $$ giving a new expression for the output of one of the network layers: $$ \mathrm{output} = \sigma(Wx + b) $$ Here, $\sigma(z)$ is called the activation function. The intention is that each layer learns a higher-level representation of the input. It turns out that neural networks with sigmoid activation functions are universal function approximators; what makes them useful is that we can train them to do so.
Notation¶
We'll use the following notation:
$L$ - Number of layers in the network.
$N^n$ - Dimensionality of layer $n \in \{0, \ldots, L\}$. $N^0$ is the dimensionality of the input; $N^L$ is the dimensionality of the output.
$W^m \in \mathbb{R}^{N^m \times N^{m - 1}}$ - Weight matrix for layer $m \in \{1, \ldots, L\}$. $W^m_{ij}$ is the weight between the $i^{th}$ unit in layer $m$ and the $j^{th}$ unit in layer $m - 1$.
$b^m \in \mathbb{R}^{N^m}$ - Bias vector for layer $m$.
$\sigma^m$ - Nonlinear activation function of the units in layer $m$, applied elementwise.
$z^m \in \mathbb{R}^{N^m}$ - Linear mix of the inputs to layer $m$, computed by $z^m = W^m a^{m - 1} + b^m$.
$a^m \in \mathbb{R}^{N^m}$ - Activation of units in layer $m$, computed by $a^m = \sigma^m(h^m) = \sigma^m(W^m a^{m - 1} + b^m)$. $a^L$ is the output of the network. We define the special case $a^0$ as the input of the network.
$y \in \mathbb{R}^{N^L}$ - Target output of the network.
$C$ - Cost/error function of the network, which is a function of $a^L$ (the network output) and $y$ (treated as a constant).
Training a Neural Network with Gradient Descent¶
In a typical setting, we want our neural network to be able to predict an output given some input based on some training data of input-output pairs $x, y$. An example used here is to predict the numerical value of a digital image of a handwritten digit. To do so, we first define a cost function: $$ C = \frac{1}{2n}\sum_x ||y - a^L||^2 $$ where the sum is over all $n$ training points $x$. If this cost function is minimized, we have obtained a neural network whose output is, on average, close to the target output over the training set. The output will depend on the neural network parameters $W^m$ and $b^m$.
The most common method for minimizing the cost function is to use gradient descent. Gradient descent simply adjusts the parameters $W^m$ and $b^m$ in a direction opposite of the gradient of the cost function, which is guaranteed to decrease the value of the cost function. To do so, we need to know the gradient of $C$ with respect $W^m$ and $b^m$ which is computed by backpropagation (not covered here). That is, gradient descent updates the parameters by $$ W^{m\prime} = W^m - \eta\frac{\partial C}{\partial W^m} $$ $$ b^{m\prime} = b^m - \eta\frac{\partial C}{\partial b^m} $$ where $\eta$ is the learning rate. Note that in practice we compute the average gradient of $C$ across a subset of the training set (a mini-batch) and update according to that.
Example: Training a Neural Network to classify MNIST¶
The following code trains a neural network with sigmoid acivation function using gradient descent to classify the MNIST dataset.
import numpy as np
import random
import cPickle
import gzip
import theano
import theano.tensor as T
import matplotlib.pyplot as plt
%matplotlib inline
def load_data():
"""Return the MNIST data as a tuple containing the training data,
the validation data, and the test data.
The ``training_data`` is returned as a tuple with two entries.
The first entry contains the actual training images. This is a
numpy ndarray with 50,000 entries. Each entry is, in turn, a
numpy ndarray with 784 values, representing the 28 * 28 = 784
pixels in a single MNIST image.
The second entry in the ``training_data`` tuple is a numpy ndarray
containing 50,000 entries. Those entries are just the digit
values (0...9) for the corresponding images contained in the first
entry of the tuple.
The ``validation_data`` and ``test_data`` are similar, except
each contains only 10,000 images.
This is a nice data format, but for use in neural networks it's
helpful to modify the format of the ``training_data`` a little.
That's done in the wrapper function ``load_data_wrapper()``, see
below.
"""
f = gzip.open('mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = cPickle.load(f)
f.close()
return (training_data, validation_data, test_data)
def load_data_wrapper():
"""Return a tuple containing ``(training_data, validation_data,
test_data)``. Based on ``load_data``, but the format is more
convenient for use in our implementation of neural networks.
In particular, ``training_data`` is a list containing 50,000
2-tuples ``(x, y)``. ``x`` is a 784-dimensional numpy.ndarray
containing the input image. ``y`` is a 10-dimensional
numpy.ndarray representing the unit vector corresponding to the
correct digit for ``x``.
``validation_data`` and ``test_data`` are lists containing 10,000
2-tuples ``(x, y)``. In each case, ``x`` is a 784-dimensional
numpy.ndarry containing the input image, and ``y`` is the
corresponding classification, i.e., the digit values (integers)
corresponding to ``x``.
Obviously, this means we're using slightly different formats for
the training data and the validation / test data. These formats
turn out to be the most convenient for use in our neural network
code."""
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_results = [vectorized_result(y) for y in tr_d[1]]
training_data = zip(training_inputs, training_results)
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = zip(validation_inputs, va_d[1])
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = zip(test_inputs, te_d[1])
return (training_data, validation_data, test_data)
def vectorized_result(j):
"""Return a 10-dimensional unit vector with a 1.0 in the jth
position and zeroes elsewhere. This is used to convert a digit
(0...9) into a corresponding desired output from the neural
network."""
e = np.zeros((10, 1))
e[j] = 1.0
return e
class Network():
def __init__(self, sizes):
"""The list ``sizes`` contains the number of neurons in the
respective layers of the network. For example, if the list
was [2, 3, 1] then it would be a three-layer network, with the
first layer containing 2 neurons, the second layer 3 neurons,
and the third layer 1 neuron. The biases and weights for the
network are initialized randomly, using a Gaussian
distribution with mean 0, and variance 1. Note that the first
layer is assumed to be an input layer, and by convention we
won't set any biases for those neurons, since biases are only
ever used in computing the outputs from later layers."""
self.num_layers = len(sizes)
self.sizes = sizes
self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(sizes[:-1], sizes[1:])]
def feedforward(self, a):
"""Return the output of the network if ``a`` is input."""
for b, w in zip(self.biases, self.weights):
a = sigmoid_vec(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
test_data=None):
"""Train the neural network using mini-batch stochastic
gradient descent. The ``training_data`` is a list of tuples
``(x, y)`` representing the training inputs and the desired
outputs. The other non-optional parameters are
self-explanatory. If ``test_data`` is provided then the
network will be evaluated against the test data after each
epoch, and partial progress printed out. This is useful for
tracking progress, but slows things down substantially."""
if test_data: n_test = len(test_data)
n = len(training_data)
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(mini_batch, eta)
if test_data:
print "Epoch {0}: {1} / {2}".format(
j, self.evaluate(test_data), n_test)
else:
print "Epoch {0} complete".format(j)
def update_mini_batch(self, mini_batch, eta):
"""Update the network's weights and biases by applying
gradient descent using backpropagation to a single mini batch.
The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
is the learning rate."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Return a tuple ``(nabla_b, nabla_w)`` representing the
gradient for the cost function C_x. ``nabla_b`` and
``nabla_w`` are layer-by-layer lists of numpy arrays, similar
to ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# feedforward
activation = x
activations = [x] # list to store all the activations, layer by layer
zs = [] # list to store all the z vectors, layer by layer
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid_vec(z)
activations.append(activation)
# backward pass
delta = self.cost_derivative(activations[-1], y) * \
sigmoid_prime_vec(zs[-1])
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
# Note that the variable l in the loop below is used a little
# differently to the notation in Chapter 2 of the book. Here,
# l = 1 means the last layer of neurons, l = 2 is the
# second-last layer, and so on. It's a renumbering of the
# scheme in the book, used here to take advantage of the fact
# that Python can use negative indices in lists.
for l in xrange(2, self.num_layers):
z = zs[-l]
spv = sigmoid_prime_vec(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * spv
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def evaluate(self, test_data):
"""Return the number of test inputs for which the neural
network outputs the correct result. Note that the neural
network's output is assumed to be the index of whichever
neuron in the final layer has the highest activation."""
test_results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in test_data]
return sum(int(x == y) for (x, y) in test_results)
def cost_derivative(self, output_activations, y):
"""Return the vector of partial derivatives \partial C_x /
\partial a for the output activations."""
return (output_activations-y)
#### Miscellaneous functions
def sigmoid(z):
"""The sigmoid function."""
return 1.0/(1.0+np.exp(-z))
sigmoid_vec = np.vectorize(sigmoid)
def sigmoid_prime(z):
"""Derivative of the sigmoid function."""
return sigmoid(z)*(1-sigmoid(z))
sigmoid_prime_vec = np.vectorize(sigmoid_prime)
training_data, validation_data, test_data = load_data_wrapper()
# Plot a few example training digits
plt.figure(figsize=(6, 6))
for n in range(9):
plt.subplot(3, 3, n)
plt.imshow(training_data[n][0].reshape(28, 28), interpolation='nearest', cmap=plt.cm.gray_r)
plt.axis('off')
plt.title(np.argmax(training_data[n][1]))
# Initialize the network
net = Network([784, 30, 10])
# Training for 10 epochs using a mini-batch size of 10, with a learning rate of 3.
net.SGD(training_data, 10, 10, 3.0, test_data=test_data)
Epoch 0: 9067 / 10000 Epoch 1: 9202 / 10000 Epoch 2: 9283 / 10000 Epoch 3: 9318 / 10000 Epoch 4: 9376 / 10000 Epoch 5: 9393 / 10000 Epoch 6: 9399 / 10000 Epoch 7: 9426 / 10000 Epoch 8: 9443 / 10000 Epoch 9: 9454 / 10000
Using Theano¶
For completeness, here's an implementation of the above using Theano based on my Theano tutorial.
class Layer(object):
def __init__(self, W_init, b_init, activation):
'''
A layer of a neural network, computes s(Wx + b) where s is a nonlinearity and x is the input vector.
:parameters:
- W_init : np.ndarray, shape=(n_output, n_input)
Values to initialize the weight matrix to.
- b_init : np.ndarray, shape=(n_output,)
Values to initialize the bias vector
- activation : theano.tensor.elemwise.Elemwise
Activation function for layer output
'''
# Retrieve the input and output dimensionality based on W's initialization
n_output, n_input = W_init.shape
# Make sure b is n_output in size
assert b_init.shape == (n_output,)
# All parameters should be shared variables.
# They're used in this class to compute the layer output,
# but are updated elsewhere when optimizing the network parameters.
# Note that we are explicitly requiring that W_init has the theano.config.floatX dtype
self.W = theano.shared(value=W_init.astype(theano.config.floatX),
# The name parameter is solely for printing purporses
name='W',
# Setting borrow=True allows Theano to use user memory for this object.
# It can make code slightly faster by avoiding a deep copy on construction.
# For more details, see
# http://deeplearning.net/software/theano/tutorial/aliasing.html
borrow=True)
# We can force our bias vector b to be a column vector using numpy's reshape method.
# When b is a column vector, we can pass a matrix-shaped input to the layer
# and get a matrix-shaped output, thanks to broadcasting (described below)
self.b = theano.shared(value=b_init.reshape(-1, 1).astype(theano.config.floatX),
name='b',
borrow=True,
# Theano allows for broadcasting, similar to numpy.
# However, you need to explicitly denote which axes can be broadcasted.
# By setting broadcastable=(False, True), we are denoting that b
# can be broadcast (copied) along its second dimension in order to be
# added to another variable. For more information, see
# http://deeplearning.net/software/theano/library/tensor/basic.html
broadcastable=(False, True))
self.activation = activation
# We'll compute the gradient of the cost of the network with respect to the parameters in this list.
self.params = [self.W, self.b]
def output(self, x):
'''
Compute this layer's output given an input
:parameters:
- x : theano.tensor.var.TensorVariable
Theano symbolic variable for layer input
:returns:
- output : theano.tensor.var.TensorVariable
Mixed, biased, and activated x
'''
# Compute linear mix
lin_output = T.dot(self.W, x) + self.b
# Output is just linear mix if no activation function
# Otherwise, apply the activation function
return (lin_output if self.activation is None else self.activation(lin_output))
class MLP(object):
def __init__(self, W_init, b_init, activations):
'''
Multi-layer perceptron class, computes the composition of a sequence of Layers
:parameters:
- W_init : list of np.ndarray, len=N
Values to initialize the weight matrix in each layer to.
The layer sizes will be inferred from the shape of each matrix in W_init
- b_init : list of np.ndarray, len=N
Values to initialize the bias vector in each layer to
- activations : list of theano.tensor.elemwise.Elemwise, len=N
Activation function for layer output for each layer
'''
# Make sure the input lists are all of the same length
assert len(W_init) == len(b_init) == len(activations)
# Initialize lists of layers
self.layers = []
# Construct the layers
for W, b, activation in zip(W_init, b_init, activations):
self.layers.append(Layer(W, b, activation))
# Combine parameters from all layers
self.params = []
for layer in self.layers:
self.params += layer.params
def output(self, x):
'''
Compute the MLP's output given an input
:parameters:
- x : theano.tensor.var.TensorVariable
Theano symbolic variable for network input
:returns:
- output : theano.tensor.var.TensorVariable
x passed through the MLP
'''
# Recursively compute output
for layer in self.layers:
x = layer.output(x)
return x
def squared_error(self, x, y):
'''
Compute the squared euclidean error of the network output against the "true" output y
:parameters:
- x : theano.tensor.var.TensorVariable
Theano symbolic variable for network input
- y : theano.tensor.var.TensorVariable
Theano symbolic variable for desired network output
:returns:
- error : theano.tensor.var.TensorVariable
The squared Euclidian distance between the network output and y
'''
return T.sum((self.output(x) - y)**2)
def gradient_updates(cost, params, learning_rate):
'''
Compute updates for gradient descent
:parameters:
- cost : theano.tensor.var.TensorVariable
Theano cost function to minimize
- params : list of theano.tensor.var.TensorVariable
Parameters to compute gradient against
- learning_rate : float
Gradient descent learning rate
:returns:
updates : list
List of updates, one for each parameter
'''
# List of update steps for each parameter
updates = []
# Just gradient descent on cost
for param in params:
# Each parameter is updated by taking a step in the opposite direction of the gradient.
updates.append((param, param - learning_rate*T.grad(cost, param)))
return updates
# First, set the size of each layer (and the number of layers)
# Input layer size is training data dimensionality - 28*28 = 784
# Output size is target dimensionality, here 1 of 10 digits, so size = 10
# Finally, let the hidden layer have 30 neurons as above.
# If we wanted more layers, we could just add another layer size to this list.
layer_sizes = [training_data[0][0].shape[0], 30, training_data[0][1].shape[0]]
# Set initial parameter values
W_init = []
b_init = []
activations = []
for n_input, n_output in zip(layer_sizes[:-1], layer_sizes[1:]):
# Getting the correct initialization matters a lot for non-toy problems.
# However, here we can just use the following initialization with success:
# Normally distribute initial weights
W_init.append(np.random.randn(n_output, n_input))
# Set initial biases to 1
b_init.append(np.ones(n_output))
# We'll use sigmoid activation for all layers
# Note that this doesn't make a ton of sense when using squared distance
# because the sigmoid function is bounded on [0, 1].
activations.append(T.nnet.sigmoid)
# Create an instance of the MLP class
mlp = MLP(W_init, b_init, activations)
# Create Theano variables for the MLP input
mlp_input = T.matrix('mlp_input')
# ... and the desired output
mlp_target = T.matrix('mlp_target')
# Number of examples in each mini-batch
batch_size = 10
# Learning rate is 3., but our MLP doesn't normalize by batch size so we do it here
learning_rate = 3./batch_size
# Create a function for computing the cost of the network given an input
cost = mlp.squared_error(mlp_input, mlp_target)
# Create a theano function for training the network
train = theano.function([mlp_input, mlp_target], cost,
updates=gradient_updates(cost, mlp.params, learning_rate))
# Create a theano function for computing the MLP's output given some input
mlp_output = theano.function([mlp_input], mlp.output(mlp_input))
# Number of times to iterate over the training set
n_epochs = 10
for epoch in range(n_epochs):
random.shuffle(training_data)
mini_batches = [training_data[k:k+batch_size] for k in xrange(0, len(training_data), batch_size)]
for mini_batch in mini_batches:
train(np.hstack(X[0] for X in mini_batch), np.hstack(X[1] for X in mini_batch))
test_output = mlp_output(np.hstack([X[0] for X in test_data]))
n_correct = np.sum(np.argmax(test_output, axis=0) == [X[1] for X in test_data])
print "Epoch {0}: {1} / {2}".format(epoch, n_correct, len(test_data))
Epoch 0: 9095 / 10000 Epoch 1: 9270 / 10000 Epoch 2: 9317 / 10000 Epoch 3: 9313 / 10000 Epoch 4: 9355 / 10000 Epoch 5: 9403 / 10000 Epoch 6: 9413 / 10000 Epoch 7: 9397 / 10000 Epoch 8: 9360 / 10000 Epoch 9: 9411 / 10000