ETHZ: 227-0966-00L¶

Quantitative Big Imaging¶

April 12, 2018¶

Advanced Shape and Texture¶

Literature / Useful References¶

Books¶

Jean Claude, Morphometry with R
Online through ETHZ
Buy it
John C. Russ, “The Image Processing Handbook”,(Boca Raton, CRC Press)
Available online within domain ethz.ch (or proxy.ethz.ch / public VPN)

Papers / Sites¶

Thickness
[1] Hildebrand, T., & Ruegsegger, P. (1997). A new method for the model-independent assessment of thickness in three-dimensional images. Journal of Microscopy, 185(1), 67–75. doi:10.1046/j.1365-2818.1997.1340694.x
Curvature
http://mathworld.wolfram.com/MeanCurvature.html
[2] "Computation of Surface Curvature from Range Images Using Geometrically Intrinsic Weights"*, T. Kurita and P. Boulanger, 1992.
http://radiomics.io

Outline¶

Motivation (Why and How?)
What are Distance Maps?
What are thickness maps?

Characteristic Shapes
Texture Analysis

Definition¶

If we start with an image as a collection of points divided into two categories

$Im(x,y)=$ {Foreground, Background}
We can define a distance map operator ( $dist$ ) that transforms the image into a distance map

$dist(\vec{x}) = \textrm{min}(||\vec{x}-\vec{y}|| \forall \vec{y} \in \textrm{Background})$

We will use Euclidean distance $||\vec{x}-\vec{y}||$ for this class but there are other metrics which make sense when dealing with other types of data like Manhattan/City-block or weighted metrics.

Distance Maps: Precaution¶

The distance map is one of the crictical points where the resolution of the imaging system is important.

We measure distances computationally in pixels or voxels
but for them to have a meaning physically they must be converted
Isotropic imaging (1 $\mu$ m x 1 $\mu$ m x 1 $\mu$ m) is fine

Anisotropic¶

Ideally

as part of filtering, resample and convert to an isotropic scale.

If that is not possible

custom distance map algorithms which use the side-lengths of the voxels to calculate distance rather than assuming 1x1x1

In [13]:

from matplotlib.animation import FuncAnimation
from IPython.display import HTML
fig, m_axs = plt.subplots(2, 3, figsize=(10, 12), dpi=100)

img_list = []
for i in np.linspace(0.6, 1.3, 7):
    img_bw = np.concatenate([generate_dot_image(12, 0.7, i),
                             generate_dot_image(12, 0.6, i)], 0)
    img_base = ndimage.distance_transform_edt(img_bw)
    img_list += [img_base]


def update_frame(i):
    [tax.cla() for tax in m_axs.flatten()]
    ((c_ax, c_hist, c_dmean), (c_lab, c_labhist, c_lmean)) = m_axs
    sns.heatmap(img_list[i],
                annot=True,
                fmt="2.0f",
                cmap='nipy_spectral',
                ax=c_ax,
                cbar=False,
                vmin=0,
                vmax=5)
    c_ax.set_title('DMap #{}'.format(i+1))
    c_hist.hist(img_list[i].ravel(),
                np.linspace(0, 3, 6))
    c_hist.set_title('Mean: %2.2f\nStd: %2.2f' % (np.mean(img_list[i][img_list[i] > 0]),
                                                  np.std(img_list[i][img_list[i] > 0])))

    c_dmean.plot(range(i+1), [np.mean(img_list[k][img_list[k] > 0])
                              for k in range(i+1)], 'r+-')
    c_dmean.set_ylim(0, 2)
    c_dmean.set_title('Avergage Distance')

    lab_img = ndimage.label(img_list[i] > 0)[0]

    sns.heatmap(lab_img,
                annot=True,
                fmt="d",
                cmap='nipy_spectral',
                ax=c_lab,
                cbar=False,
                vmin=0,
                vmax=2)
    c_lab.set_title('Component Labeled')

    def avg_area(c_img):
        l_img = ndimage.label(c_img > 0)[0]
        return np.mean([np.sum(l_img == k) for k in range(1, l_img.max()+1)])
    n, _, _ = c_labhist.hist(lab_img[lab_img > 0].ravel(), [
                             0, 1, 2, 3], rwidth=0.8)
    c_labhist.set_title('# Components: %d\nAvg Area: %d' %
                        (lab_img.max(), avg_area(img_list[i])))

    c_lmean.plot(range(i+1),
                 [avg_area(img_list[k]) for k in range(i+1)], 'r+-')
    c_lmean.set_ylim(0, 150)
    c_lmean.set_title('Average Area')


# write animation frames
anim_code = FuncAnimation(fig,
                          update_frame,
                          frames=len(img_list)-1,
                          interval=1000,
                          repeat_delay=2000).to_html5_video()
plt.close('all')
HTML(anim_code)

Out[13]:

Thickness Map: What is it?¶

Thickness is a metric for assessing the size and structure of objects in a very generic manner. For every point $\vec{x}$ in the image you find the largest sphere which:

contains that point
is entirely contained within the object

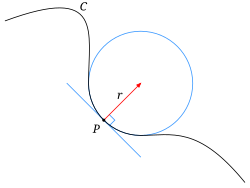
Thickness Diagram Taken from [1]

The image shows a typical object
The sphere centered at point $p$ with a radius $r$ is the largest that fits

Application¶

Ideal for spherical and cylindrical objects since it shows their radius
Also relevant for flow and diffusion since it can highlight bottlenecks in structure

Meshing¶

Constructing a mesh for an image provides very different information than the image data itself. Most crucially this comes when looking at physical processes like deformation.

While the images are helpful for visualizing we rarely have models for quantifying how difficult it is to turn a pixel off

If the image is turned into a mesh we now have a list of vertices and edges. For these vertices and edges we can define forces. For example when looking at stress-strain relationships in mechanics using Hooke's Model $\vec{F}=k (\vec{x}_0-\vec{x})$ the force needed to stretch one of these edges is proportional to how far it is stretched.

Curvature¶

Curvature is a metric related to the surface or interface between phases or objects.

It is most easily understood in its 1D sense or being the radius of the circle that matchs the local shape of a curve

Mathematically it is defined as

$\kappa = \frac{1}{R}$

Thus a low curvature means the value means a very large radius and high curvature means a very small radius

Curvature: Surface Normal¶

In order to meaningfully talk about curvatures of surfaces, we first need to define a consistent frame of reference for examining the surface of an object. We thus define a surface normal vector as a vector oriented orthogonally to the surface away from the interior of the object $\rightarrow \vec{N}$

Surface Surface Normals

Curvature: 3D¶

With the notion of surface normal defined ( $\vec{N}$ ), we can define many curvatures at point $\vec{x}$ on the surface.

This is because there are infinitely many planes which contain both point $\vec{x}$ and $\vec{N}$
More generally we can define an angle $\theta$ about which a single plane containing both can be freely rotated
We can then define two principal curvatures by taking the maximum and minimum of this curve

$\kappa_1 = \textrm{max}(\kappa(\theta))$

$\kappa_2 = \textrm{min}(\kappa(\theta))$

Mean Curvature¶

The mean of the two principal curvatures $H = \frac{1}{2}(\kappa_1+\kappa_2)$

Gaussian Curvature¶

The mean of the two principal curvatures $K = \kappa_1\kappa_2$

positive for spheres (or spherical inclusions)
curvatures agree in sign
negative for saddles (hyperboloid surfaces)
curvatures disgree in sign
0 for planes

Other Techniques¶

There are hundreds of other techniques which can be applied to these complicated structures, but they go beyond the scope of this course. Many of them are model-based which means they work well but only for particular types of samples or images. Of the more general techniques several which are easily testable inside of FIJI are

Directional Analysis = Looking at the orientation of different components using Fourier analysis (Analyze $\rightarrow$ Directionality)
Tubeness / Surfaceness (Plugins $\rightarrow$ Analyze $\rightarrow$ ) characterize binary images and the shape at each point similar to curvature but with a different underlying model

Fractal Dimensionality = A metric for assessing the structure as you scale up and down by examining various spatial relationships
Ma, D., Stoica, A. D., & Wang, X.-L. (2009). Power-law scaling and fractal nature of medium-range order in metallic glasses. Nature Materials, 8(1), 30–4. doi:10.1038/nmat2340
Two (or more) point correlation functions = Used in theoretical material science and physics to describe random materials and can be used to characterize distances, orientations, and organization in complex samples
Jiao, Y., Stillinger, F., & Torquato, S. (2007). Modeling heterogeneous materials via two-point correlation functions: Basic principles. Physical Review E, 76(3). doi:10.1103/PhysRevE.76.031110
Andrey, P., Kiêu, K., Kress, C., Lehmann, G., Tirichine, L., Liu, Z., … Debey, P. (2010). Statistical analysis of 3D images detects regular spatial distributions of centromeres and chromocenters in animal and plant nuclei. PLoS Computational Biology, 6(7), e1000853. doi:10.1371/journal.pcbi.1000853
Haghpanahi, M., & Miramini, S. (2008). Extraction of morphological parameters of tissue engineering scaffolds using two-point correlation function, 463–466. Retrieved from http://portal.acm.org/citation.cfm?id=1713360.1713456

Co-occurrence matrix¶

$C_{\Delta x, \Delta y}(i,j)=\sum_{x=1}^n\sum_{y=1}^m\begin{cases} 1, & \text{if }I(x, y)=i\text{ and }I(x+\Delta x, y+\Delta y)=j \\ 0, & \text{otherwise}\end{cases}$

As text $\rightarrow$ for every possible offset $\vec{r}$ = ( $\Delta x$ , $\Delta y$ ) given the current intensity ( $i$ ) how likely is it that value at a point offset by that amount is $j$ .
This is similar to the two point correlation function but is a 4D representation instead of just a 2D
In order to use this we need to discretize the image into bins

{r}
bin_it<-function(x) as.numeric(as.factor(cut_interval(x,4)))
bin_image<-text_imgs %>% 
  mutate(value=bin_it(value)) 
bin_image %>%
  group_by(variable,value) %>%
  summarize(count=n()) %>%
  ggplot(aes(value,count))+
  geom_bar(aes(fill=variable),alpha=0.5,stat="identity",pos="dodge")+
  facet_grid(~variable)+
  theme_bw(10)

Simple Correlation¶

Using the mean difference ( $E[i-j]$ ) instead of all of the i,j pair possiblities

{r}
bin_image %>% 
  merge(bin_image,by=c("variable")) %>% 
  mutate(dx=x.y-x.x,dy=y.y-y.x,dv=value.y-value.x) %>% 
  subset((abs(dx)<4) & (abs(dy)<4)) %>%
  group_by(variable,dx,dy,value.x,value.y) %>%
  summarize(score=mean(dv)) %>%
  ggplot(aes(dx,dy))+
  geom_raster(aes(fill=score))+
  facet_wrap(~variable)+
  coord_equal()+
  theme_bw(10)

Radial Coordinates¶

Rather than using $\Delta x$ and $\Delta y$ we can also show the relative positions

{r}
bin_image %>% 
  merge(bin_image,by=c("variable")) %>% 
  mutate(dr=sqrt((x.y-x.x)**2+(y.y-y.x)**2),
         dtheta=180/pi*atan((y.y-y.x)/(x.y-x.x)),
         dv=value.y-value.x) %>% 
  subset(dr<6 & !is.na(dtheta)) %>%
  mutate(dr=cut_interval(dr,10),
         dtheta=cut_interval(dtheta,8)) %>%
  group_by(variable,dr,dtheta,value.x,value.y) %>%
  summarize(score=mean(dv)) %>%
  ggplot(aes(dtheta,dr))+
  geom_tile(aes(fill=score))+
  facet_wrap(~variable)+
  coord_polar(theta="x")+
  scale_fill_distiller(palette = "Spectral")+
  theme_bw(10)

In [14]:

# compute some GLCM properties each patch
from skimage.feature import greycomatrix, greycoprops
from tqdm import tqdm_notebook as tqdm
grayco_prop_list = ['contrast', 'dissimilarity',
                    'homogeneity', 'energy',
                    'correlation', 'ASM']

prop_imgs = {}
for c_prop in grayco_prop_list:
    prop_imgs[c_prop] = np.zeros_like(cortex_img, dtype=np.float32)
score_img = np.zeros_like(cortex_img, dtype=np.float32)
out_df_list = []
for patch_idx in tqdm(np.unique(region_labels)):
    xx_box, yy_box = np.where(region_labels == patch_idx)

    glcm = greycomatrix(cortex_img[xx_box.min():xx_box.max(),
                                   yy_box.min():yy_box.max()],
                        [5], [0], 256, symmetric=True, normed=True)

    mean_score = np.mean(cortex_mask[region_labels == patch_idx])
    score_img[region_labels == patch_idx] = mean_score

    out_row = dict(
        intensity_mean=np.mean(cortex_img[region_labels == patch_idx]),
        intensity_std=np.std(cortex_img[region_labels == patch_idx]),
        score=mean_score)

    for c_prop in grayco_prop_list:
        out_row[c_prop] = greycoprops(glcm, c_prop)[0, 0]
        prop_imgs[c_prop][region_labels == patch_idx] = out_row[c_prop]

    out_df_list += [out_row]

Failed to display Jupyter Widget of type HBox.

If you're reading this message in the Jupyter Notebook or JupyterLab Notebook, it may mean that the widgets JavaScript is still loading. If this message persists, it likely means that the widgets JavaScript library is either not installed or not enabled. See the Jupyter Widgets Documentation for setup instructions.

If you're reading this message in another frontend (for example, a static rendering on GitHub or NBViewer), it may mean that your frontend doesn't currently support widgets.

C:\Miniconda3\envs\qbi2018\lib\site-packages\skimage\feature\texture.py:109: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
  if np.issubdtype(image.dtype, np.float):

	ASM	contrast	correlation	dissimilarity	energy	homogeneity	intensity_mean	intensity_std	score
count	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000	99.000000
mean	0.045523	888.349768	0.468967	15.933864	0.128972	0.179556	61.214533	28.922878	0.159290
std	0.096791	1736.226189	0.268096	10.016607	0.170833	0.173307	32.747924	20.736974	0.310034
min	0.000366	14.721364	-0.094922	1.666023	0.019123	0.033100	1.274123	3.241296	0.000000
25%	0.000626	249.179078	0.247538	11.847264	0.025010	0.070740	39.180681	14.174057	0.000000
50%	0.000904	334.321682	0.504085	13.734549	0.030073	0.082297	62.908854	20.017975	0.000000
75%	0.036697	779.776342	0.677313	18.028875	0.191400	0.250455	80.434896	35.653407	0.078170
max	0.424854	13619.651391	0.958805	82.260229	0.651809	0.718922	131.299479	94.529072	1.000000