Survival Modeling in Stan¶
-- TODO insert image here
a very brief introduction¶
Survival analysis typically involves time to event as the outcome of interest
Typical applications include:
- biomedical research (time to clinical event or death)
- digital marketing (time to click or KPI)
- machine (time to mechanical failure)
- psychology (e.g. studies of delayed gratification)
- ... etc
key terms¶
- censoring: when an event isn't observed, but we know
- it happened after time
b(right censoring) - it happened before time
a(left censoring) - it happened between times
aandb(interval censoring)
- it happened after time
Survival analysis typically makes an assumption of non-informative censoring.
If this assumption holds, it means that the true event time (if it were to be observed) is unrelated to the censored time.
In a context of a well-designed clinical trial, this assumption is addressed by the study design which imposes an independent censoring process.
For example, it's not uncommon for follow-up time to be truncated after a predetermined time $t=10$ for all patients.
plot_example()
however, this assumption can sometimes be violated if, for example, less healthy patients are more likely to drop out of the study early.
key terms (cont'd)¶
- failure event: the outcome event of interest
- survival: not failure
- hazard: risk for failure events
Survival
We first define a Survival function $S$ as the probability of surviving to time $t$:
$$ S(t)=Pr(Y > t) $$
where $T$ is the true survival time.
hazard
We also define the instantaneous hazard function $\lambda$ as the probability of a failure event occuring in the interval [$t$, $t+\delta t$], given survival to time $t$:
$$ \lambda(t) = \lim_{\delta t \rightarrow 0 } \; \frac{Pr( t \le Y \le t + \delta t | Y > t)}{\delta t} $$
Which is equal to
$$ \lambda(t) = \frac{-S'(t)}{S(t)} $$
Solving this
$$ \lambda(t) = \frac{-S'(t)}{S(t)} $$
yields the following:
$$ S(t) = \exp\left( -\int_0^t \lambda(z) dz \right) $$
which provides a useful way for us to switch from modeling hazards to modeling Survival.
The integral in this equation is also sometimes called the cumulative hazard, here noted as $H(t)$.
$$ H(t) = \int_0^t \lambda(z) dz $$
It's worth pointing out that, by definition, the cumulative hazard (estimating $Pr(Y \lt t)$) is the complementary c.d.f of the Survival function (which estimates $Pr(Y \ge t)$).
Let's consider a simple hazard function $\lambda(t)$ as constant over time.
$$ \lambda(t) = a $$
Cumulative hazard ($H$) would be:
$$ H(t) = \int_0^t \lambda(z) dz = at $$
And the Survival function would be:
$$ S(t) = \exp\left( -\int_0^t \lambda(z) dz \right) = \exp ( − a t ) $$
Graphically, this would look like the following:
plot_survival_exp(N = 1000, censor_time = 10, rate = 0.5)
We can also simulate survival times for a population under this fairly simple model.
# define a function to simulate data
def simulate_exp_survival_data(N, censor_time, rate):
## simulate true lifetimes (t) according to exponential model
sample_data = pd.DataFrame({
'true_t': np.random.exponential((1/rate), size=N)
})
## censor observations at censor_time
sample_data['t'] = np.minimum(sample_data['true_t'], censor_time)
sample_data['event'] = sample_data['t'] >= sample_data['true_t']
return(sample_data)
# simulate data assuming constant hazard over time of 0.5
df = simulate_exp_survival_data(N = 100, censor_time = 6, rate = 0.5)
df.head()
| true_t | t | event | |
|---|---|---|---|
| 0 | 0.137413 | 0.137413 | True |
| 1 | 4.310870 | 4.310870 | True |
| 2 | 1.685407 | 1.685407 | True |
| 3 | 2.228120 | 2.228120 | True |
| 4 | 0.632862 | 0.632862 | True |
# plot lifelines for this simulated sample
plot_lifetimes(event_observed=df.event, lifetimes=df.t)
# calculate number of people surviving at each time T
# plot Survival to time t given simulated data
a = plot_cum_survival(df.t, df.event)
_ = plt.title('Simulated survival with $\lambda={}$'.format(0.5), size=20)
Now, overlay computed Survival from simulated data with estimated c.d.f
a = plot_cum_survival(df.t, df.event)
## overlay c.d.f. estimate as exp(-at)
test = pd.DataFrame([{
't': t,
'Estimated Surv': np.exp(-1 * 0.5 * t)
} for t in np.linspace(0, 10, num=100)])
_ = plt.plot(test.t, test['Estimated Surv'], 'b')
_ = plt.legend()
the likelihood¶
The data for survival analysis typically constitute a set of observed pairs: [t, status] for each subject, where
tis the survival time (last time a subject was observed alive)statusis a binary (T/F or 1/0) indicator for whether the failure event occurred at timet.
The likelihood for an observation $i$ with time $t_i$ and status = 1 (DECEASED) will reflect the joint probability of surviving to time $t$ and having an event at time $t$:
$$ L_i = f(t_i) = S(t_i)\lambda(t_i) $$
For an observation that is censored at time $t$, we only have a contribution to the Survival function :
$$ L_i = f(t_i) = S(t_i) $$
Most of the time, we are interested in modeling the impact of covariates on these outcomes.
The typical starting point is to make what's called the Proportional Hazards assumption.
IE:
$$ h_X(t_i) = e^{\beta X}h(t_i) $$
For example, in the context of our previous example of Survival times simulated according to the Exponential model, we have:
# define a function to simulate data
def simulate_exp_survival_data_X(N, censor_time, rate, beta):
## simulate true lifetimes (t) according to exponential model
sample_data = pd.DataFrame({
'X' : [np.random.uniform()>0.5 for n in np.zeros(N)],
'baseline_hazard': np.repeat(rate, repeats=N),
})
sample_data['hazard'] = np.exp(beta*sample_data['X'])*sample_data['baseline_hazard']
sample_data['true_t'] = sample_data.apply(lambda row: np.random.exponential(scale = 1/row['hazard']), axis = 1)
## censor observations at censor_time
sample_data['t'] = np.minimum(sample_data['true_t'], censor_time)
sample_data['event'] = sample_data['t'] >= sample_data['true_t']
return(sample_data)
df = simulate_exp_survival_data_X(N=100, censor_time=6, rate=0.9, beta=0.2)
plot_cum_survival_X(df)
<matplotlib.figure.Figure at 0x7f4b5dd7d410>
# fit exponential model to these data
import stanity
import survivalstan
models = survivalstan.utils.read_files('stan')
stan/exp_survival_model.stan stan/pem_survival_model_unstructured.stan stan/pem_survival_model_gamma.stan stan/pem_survival_model_randomwalk_bspline_est_xi.stan stan/pem_survival_model_randomwalk.stan stan/pem_survival_model_randomwalk_bspline.stan stan/weibull_survival_model.stan
weib_model = survivalstan.fit_stan_survival_model(df = df,
formula = '~ X',
event_col = 'event',
time_col = 't',
model_code = survivalstan.models.weibull_survival_model,
chains = 4,
iter = 5000,
make_inits = survivalstan.make_weibull_survival_model_inits,
model_cohort = 'exp simulated, weibull model'
)
NOT reusing model. Ran in 66.599 sec.
/mnt/ssd0/env/local/lib/python2.7/site-packages/stanity/psis.py:228: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison elif sort == 'in-place': /mnt/ssd0/env/local/lib/python2.7/site-packages/stanity/psis.py:246: VisibleDeprecationWarning: using a non-integer number instead of an integer will result in an error in the future bs /= 3 * x[sort[np.floor(n/4 + 0.5) - 1]]
sb.boxplot(data=weib_model['coefs'], x = 'value', y = 'variable')
plt.title('Posterior estimates of model coefficients, simulated data', size = 15)
<matplotlib.text.Text at 0x7f4b8145a150>
## try with exponential baseline hazard
exp_model = survivalstan.fit_stan_survival_model(df = df,
model_code = models['exp_survival_model.stan'],
formula = '~ X',
model_cohort = 'exp simulated, exp model',
event_col = 'event',
time_col = 't',
chains = 4,
iter = 5000,
)
NOT reusing model. Ran in 55.863 sec.
survivalstan.utils.plot_coefs(models = [exp_model, weib_model])
plt.title('Posterior estimates of model coefficients, simulated data', size = 15)
<matplotlib.text.Text at 0x7f4b5d6bb4d0>
stanity.loo_compare(weib_model['loo'], exp_model['loo'])
{'diff': 0.39328730440969473, 'se_diff': 0.52756534110618469}
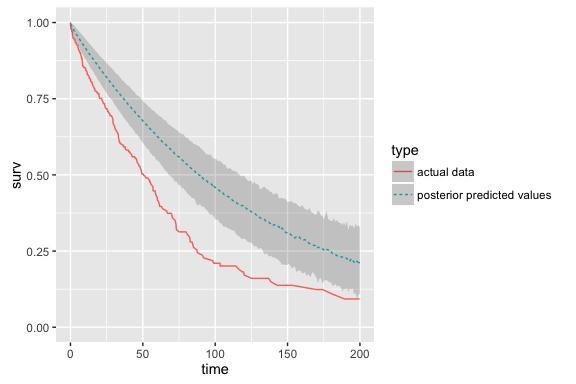
Posterior predictive checking
Basic strategy:
- Compute posterior estimates of y, assuming no censoring
- For each iteration, summarize proportion of population surviving to time
t - Summarize survival over iterations (requires selecting desired summary timepoints)
## example for exponential model - extract `yhat_uncens` observations
posterior_preds = survivalstan.utils.extract_params_long(models=[exp_model], element='yhat_uncens')
posterior_preds.rename(columns = {'variable': 'index', 'value': 'ppred_t'}, inplace=True)
posterior_preds['ppred_event'] = True
posterior_preds.head()
| iter | index | ppred_t | model_cohort | ppred_event | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0.129399 | exp simulated, exp model | True |
| 1 | 1 | 0 | 1.745296 | exp simulated, exp model | True |
| 2 | 2 | 0 | 0.240160 | exp simulated, exp model | True |
| 3 | 3 | 0 | 0.167429 | exp simulated, exp model | True |
| 4 | 4 | 0 | 1.361147 | exp simulated, exp model | True |
## for each iteration, summarize cumulative survival at each observed timepoint
posterior = posterior_preds.groupby(['iter']).apply(
lambda row: survival_table_from_events(event_observed=row['ppred_event'], death_times=row['ppred_t']),
)
## rename variables
## (should really be done by model cohort, but ok here since max is same for both groups)
posterior['Survival'] = posterior['at_risk']/max(posterior['at_risk'])
posterior.reset_index(inplace=True)
posterior.head()
| iter | event_at | removed | observed | censored | entrance | at_risk | Survival | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.000000 | 0.0 | 0.0 | 0.0 | 100.0 | 100.0 | 1.00 |
| 1 | 0 | 0.001416 | 1.0 | 1.0 | 0.0 | 0.0 | 100.0 | 1.00 |
| 2 | 0 | 0.002300 | 1.0 | 1.0 | 0.0 | 0.0 | 99.0 | 0.99 |
| 3 | 0 | 0.025914 | 1.0 | 1.0 | 0.0 | 0.0 | 98.0 | 0.98 |
| 4 | 0 | 0.033246 | 1.0 | 1.0 | 0.0 | 0.0 | 97.0 | 0.97 |
## summarize over intervals
sb.boxplot(data = ppsummary,
x = 'time_interval',
y = 'Survival',
fliersize=0)
<matplotlib.axes._subplots.AxesSubplot at 0x7f4b5d6b7690>
plot_cum_survival(event=df.event, t=df.t)
_ = plt.fill_between(ppsummary2.interval_t,
ppsummary2.Survival_p10,
ppsummary2.Survival_p90,
where= ppsummary2.Survival_p90 >= ppsummary2.Survival_p10,
facecolor='gray')
These checks can be useful, in two ways:
- In practice, we don't know the true shape of the baseline hazard.
- Also, it can help uncover problems in the process of data-simulation and/or estimation.
Modeling the baseline hazard¶
There are a variety of methods used to model the baseline hazard.
Parametric:
- Gamma
- exponential
- Weibull
Semi- or non-parametric:
- Gamma, Weibull or exponential priors on hazards
- Gamma-process priors
- random-walk priors
- unconstrained piecewise hazard
Often we want to find a way to fit baseline hazards more flexibly, in order to better understand covariate effects.
One approach to this is to use a "binned likelihood".
unique_failure_times=df['t'].unique()
for ftime in unique_failure_times:
plt.vlines(ftime, 0, 100, lw=0.5, linestyles="--")
plot_lifetimes(event_observed=df.event, lifetimes=df.t)
## transform data
dflong = survivalstan.prep_data_long_surv(df=df.reset_index(), event_col='event', time_col='t')
dflong.sort_values(['t']).head()
| index | X | baseline_hazard | hazard | true_t | t | event | key | end_time | end_failure | |
|---|---|---|---|---|---|---|---|---|---|---|
| 3535 | 35 | True | 0.9 | 1.099262 | 0.004904 | 0.004904 | True | 1 | 0.004904 | True |
| 7535 | 75 | True | 0.9 | 1.099262 | 0.018886 | 0.018886 | True | 1 | 0.004904 | False |
| 7575 | 75 | True | 0.9 | 1.099262 | 0.018886 | 0.018886 | True | 1 | 0.018886 | True |
| 775 | 7 | False | 0.9 | 0.900000 | 0.023054 | 0.023054 | True | 1 | 0.018886 | False |
| 707 | 7 | False | 0.9 | 0.900000 | 0.023054 | 0.023054 | True | 1 | 0.023054 | True |
unstructured baseline hazard¶
Now that we have prepared our data in the right format, we are ready to fit the PEM model.
The first model we will consider is what I call an "unstructured" baseline hazard, since each timepoint is estimated somewhat independently from one another.
We have an overall average hazard, called log_baseline_mu, and the hazard for each time period is estimated as an offset from this overall mean.
Here is our parameters block:
parameters {
vector[T] log_baseline_raw; // unstructured baseline hazard for each timepoint t
vector[M] beta; // beta for each covariate
real<lower=0> baseline_sigma;
real log_baseline_mu;
}
and, our transformed parameters block:
transformed parameters {
vector[N] log_hazard;
vector[T] log_baseline; // unstructured baseline hazard for each timepoint t
log_baseline = log_baseline_raw + log_t_dur; // adjust for duration of each time period
for (n in 1:N) {
log_hazard[n] = log_baseline_mu + log_baseline[t[n]] + x[n,]*beta;
}
}
Our model block simply puts a prior on the log_baseline_mu & log_baseline_raw parameters.
model {
beta ~ cauchy(0, 2);
event ~ poisson_log(log_hazard);
log_baseline_mu ~ normal(0, 1);
baseline_sigma ~ normal(0, 1);
log_baseline_raw ~ normal(0, baseline_sigma);
}
## fit unstructured-hazard model to these data
pem_unstr = survivalstan.fit_stan_survival_model(df = dflong,
formula = '~ X',
event_col = 'end_failure',
timepoint_end_col = 'end_time',
sample_col = 'index',
model_code = models['pem_survival_model_unstructured.stan'],
chains = 4,
iter = 1000,
model_cohort = 'exp simulated, unstructured hazard',
)
NOT reusing model. Ran in 97.042 sec.
Not surprisingly, we find little evidence that the hazard varies across timepoints.
survivalstan.utils.plot_coefs([pem_unstr], element='baseline_raw')
How does the coefficient estimate from this unstructured model compare to that from our Weibull & Exponential models?
survivalstan.utils.plot_coefs([pem_unstr, weib_model, exp_model])
Random-walk baseline hazard¶
An alternative to the unstructured baseline hazard is to use what's called a random walk baseline hazard.
This is a slight modification from the previous baseline hazard, such that each time period has a hazard is an offset from (i.e. borrows information from) the hazard estimate from the the previous time period.
There are several ways to specify a random walk, such as by imposing a correlation structure on the estimates of baseline hazards. Here we have written the baseline hazard very explicitly in our model block, as follows:
model {
# [ ... some code omitted ... ]
log_baseline_raw[1] ~ normal(0, 1);
for (i in 2:T) {
log_baseline_raw[i] ~ normal(log_baseline_raw[i-1], baseline_sigma);
}
}
## fit randomwalk-prior model to these data
pem_randomwalk = survivalstan.fit_stan_survival_model(df = dflong,
formula = '~ X',
event_col = 'end_failure',
timepoint_end_col = 'end_time',
sample_col = 'index',
model_code = models['pem_survival_model_randomwalk.stan'],
chains = 1,
iter = 5000,
model_cohort = 'exp simulated, random walk prior hazard'
)
NOT reusing model. Ran in 552.588 sec.
The resulting baseline_raw hazard estimates from this model reflect the structure we imposed on the sample -- recall that we only have a sample size of n=100.
In this model, our baseline hazard has an overall mean (log_baseline_mu) and the deviance from that mean is allowed to vary from one timepoint to the next.
Let's see what this looks like in practice:
survivalstan.utils.plot_coefs([pem_randomwalk], element='baseline_raw')
Now, a perhaps the more important question is how this variance in our baseline hazard impacts our coefficient estimates.
survivalstan.utils.plot_coefs([pem_unstr, pem_randomwalk, weib_model, exp_model])
In general, it appears that these models behave very similarly -- which is good.
Let's compare to the "True" beta (the value used to simulate the data) of 0.2.
survivalstan.utils.plot_coefs([pem_unstr, pem_randomwalk, weib_model, exp_model])
plt.vlines(0.2, -200, 200, linestyles='--')
<matplotlib.collections.LineCollection at 0x7f4b759f0990>
Compare model fit with unstructured baseline hazard to that with random walk. Is there a difference between the two models according to PSIS-LOO?
stanity.loo_compare(pem_unstr['loo'], pem_randomwalk['loo'])
{'diff': 6.7186238987099252, 'se_diff': 5.0038264166095843}
For this model, we wouldn't expect a strong difference between these two models, since the true hazard we used to simulate the data did not vary over time. In practice, hazards can and sometimes do vary over time.
One of the challenges of survival analysis in practice, particularly with small sample sizes, is to stabilize the estimates of the baseline hazard, since our inferences for coefficient effects are multiplicative on this hazard.
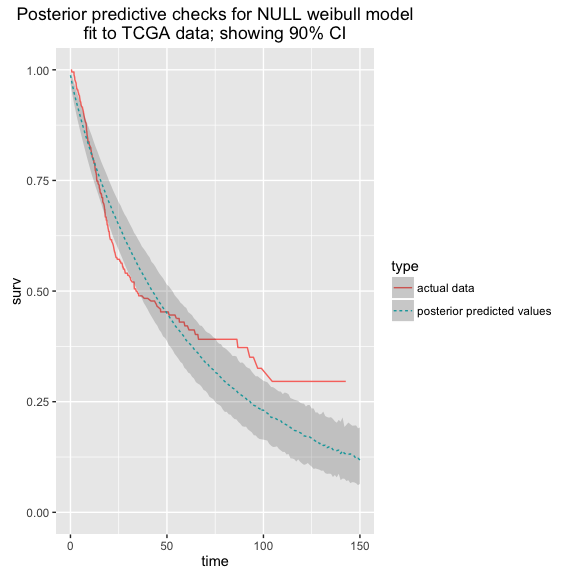
In a companion notebook, we work through a process for analyzing data from [TCGA](https://tcga-data.nci.nih.gov/tcga/tcgaCancerDetails.jsp?diseaseType=BLCA&diseaseName=Bladder Urothelial Carcinoma), focusing on the BLCA cohort.