Example-Dependent Cost-Sensitive Fraud Detection using CostCla
Alejandro Correa Bahnsen, PhD
Data Scientist

PyCaribbean, Santo Domingo, Dominican Republic, Feb 2016
About Me
A brief bio:¶
- PhD in Machine Learning at Luxembourg University
- Data Scientist at Easy Solutions
- Worked for +8 years as a data scientist at GE Money, Scotiabank and SIX Financial Services
- Bachelor in Industrial Engineering and Master in Financial Engineering
- Organizer of Big Data & Data Science Bogota Meetup
- Sport addict, love to swim, play tennis, squash, and volleyball, among others.
| al.bahnsen@gmail.com | |
| http://github.com/albahnsen | |
| http://linkedin.com/in/albahnsen | |
| @albahnsen |
Agenda¶
- Quick Intro to Fraud Detection
- Financial Evaluation of a Fraud Detection Model
- Example-Dependent Classification
- CostCla Library
- Conclusion and Future Work
Fraud Detection¶
Estimate the probability of a transaction being fraud based on analyzing customer patterns and recent fraudulent behavior
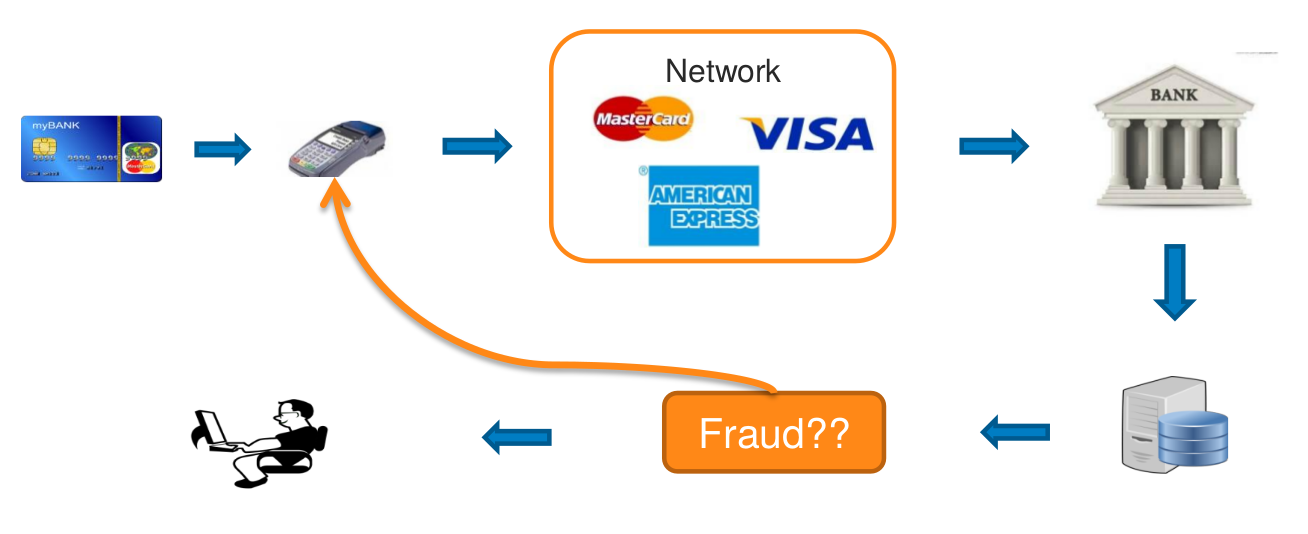
Fraud Detection¶
Issues when constructing a fraud detection system:
- Skewness of the data
- Cost-sensitivity
- Short time response of the system
- Dimensionality of the search space
- Feature preprocessing
- Model selection
Different machine learning methods are used in practice, and in the literature: logistic regression, neural networks, discriminant analysis, genetic programing, decision trees, random forests among others
Fraud Detection¶
Formally, a fraud detection is a statistical model that allows the estimation of the probability of transaction $i$ being a fraud ($y_i=1$)
$$\hat p_i=P(y_i=1|\mathbf{x}_i)$$
Data!

Load dataset from CostCla package¶
import pandas as pd
import numpy as np
from costcla import datasets
data = datasets.load_fraud()
Data file¶
print(data.keys())
print('Number of examples ', data.target.shape[0])
dict_keys(['data', 'target', 'name', 'cost_mat', 'DESCR', 'feature_names', 'target_names']) Number of examples 207147
Class Label¶
target = pd.DataFrame(pd.Series(data.target).value_counts(), columns=('Frequency',))
target['Percentage'] = (target['Frequency'] / target['Frequency'].sum()) * 100
target.index = ['Negative (Legitimate Trx)', 'Positive (Fraud Trx)']
target.loc['Total Trx'] = [data.target.shape[0], 1.]
print(target)
Frequency Percentage Negative (Legitimate Trx) 206261 99.572284 Positive (Fraud Trx) 886 0.427716 Total Trx 207147 1.000000
Features¶
pd.DataFrame(data.feature_names[:4], columns=('Features',))
| Features | |
|---|---|
| 0 | date |
| 1 | account |
| 2 | amount |
| 3 | type |
Features¶
df = pd.DataFrame(data.data[:, :4], columns=data.feature_names[:4])
df.head(10)
| date | account | amount | type | |
|---|---|---|---|---|
| 0 | 2013-01-19 17:31:46 | 1207 | 502.52 | 200 |
| 1 | 2013-01-19 17:31:25 | 1207 | 502.52 | 200 |
| 2 | 2013-01-19 17:27:48 | 1207 | 1485.71 | 200 |
| 3 | 2013-01-19 17:25:52 | 191 | 1941.74 | 200 |
| 4 | 2013-01-19 17:12:38 | 1469 | 20.6 | 200 |
| 5 | 2013-01-19 17:12:21 | 1469 | 440.42 | 200 |
| 6 | 2013-01-19 17:11:58 | 1469 | 2073.57 | 200 |
| 7 | 2013-01-19 17:11:00 | 1207 | 502.52 | 200 |
| 8 | 2013-01-19 17:10:32 | 3600 | 4991.27 | 200 |
| 9 | 2013-01-19 17:10:00 | 5806 | 20.85 | 200 |
Aggregated Features¶
df = pd.DataFrame(data.data[:, 4:], columns=data.feature_names[4:])
df.head(10)
| Trx_sum_6H | Trx_count_6H | Trx_sum_1D | Trx_count_1D | Trx_sum_2D | Trx_count_2D | Trx_sum_7D | Trx_count_7D | Trx_sum_15D | Trx_count_15D | Trx_sum_30D | Trx_count_30D | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2757.74 | 4 | 2757.74 | 4 | 2757.74 | 4 | 2757.74 | 4 | 2757.74 | 4 | 2757.74 | 4 |
| 1 | 2255.22 | 3 | 2255.22 | 3 | 2255.22 | 3 | 2255.22 | 3 | 2255.22 | 3 | 2255.22 | 3 |
| 2 | 769.51 | 2 | 769.51 | 2 | 769.51 | 2 | 769.51 | 2 | 769.51 | 2 | 769.51 | 2 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 2513.99 | 2 | 2513.99 | 2 | 7674.54 | 3 | 15523.6 | 10 | 39894.8 | 27 | 58058 | 48 |
| 5 | 2073.57 | 1 | 2073.57 | 1 | 7234.12 | 2 | 15083.2 | 9 | 39454.4 | 26 | 57617.6 | 47 |
| 6 | 0 | 0 | 0 | 0 | 5160.55 | 1 | 13009.6 | 8 | 37380.8 | 25 | 55544.1 | 46 |
| 7 | 266.99 | 1 | 266.99 | 1 | 266.99 | 1 | 266.99 | 1 | 266.99 | 1 | 266.99 | 1 |
| 8 | 588.22 | 2 | 588.22 | 2 | 588.22 | 2 | 1086.83 | 4 | 4722.14 | 11 | 11529.4 | 15 |
| 9 | 0 | 0 | 0 | 0 | 20.85 | 1 | 20.85 | 1 | 20.85 | 1 | 20.85 | 1 |
Fraud Detection as a classification problem¶
Split in training and testing¶
from sklearn.cross_validation import train_test_split
X = data.data[:, [2, 3] + list(range(4, data.data.shape[1]))].astype(np.float)
X_train, X_test, y_train, y_test, cost_mat_train, cost_mat_test = \
train_test_split(X, data.target, data.cost_mat, test_size=0.33, random_state=10)
Fraud Detection as a classification problem¶
Fit models¶
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
classifiers = {"RF": {"f": RandomForestClassifier()},
"DT": {"f": DecisionTreeClassifier()}}
ci_models = ['DT', 'RF']
# Fit the classifiers using the training dataset
for model in classifiers.keys():
classifiers[model]["f"].fit(X_train, y_train)
classifiers[model]["c"] = classifiers[model]["f"].predict(X_test)
classifiers[model]["p"] = classifiers[model]["f"].predict_proba(X_test)
classifiers[model]["p_train"] = classifiers[model]["f"].predict_proba(X_train)
Models performance¶
Evaluate metrics and plot results¶
from sklearn.metrics import f1_score, precision_score, recall_score, accuracy_score
measures = {"F1Score": f1_score, "Precision": precision_score,
"Recall": recall_score, "Accuracy": accuracy_score}
results = pd.DataFrame(columns=measures.keys())
for model in ci_models:
results.loc[model] = [measures[measure](y_test, classifiers[model]["c"]) for measure in measures.keys()]
Models performance¶
fig_acc()
Models performance¶
fig_f1()
Models performance¶
- None of these measures takes into account the business and economical realities that take place in fraud detection.
- Losses due to fraud or customer satisfaction costs, are not considered in the evaluation of the different models.
Financial Evaluation of a Fraud Detection Model
Motivation¶
- Typically, a fraud model is evaluated using standard cost-insensitive measures.
- However, in practice, the cost associated with approving a fraudulent transaction (False Negative) is quite different from the cost associated with declining a legitimate transaction (False Positive).
- Furthermore, the costs are not constant among transactions.
Cost Matrix¶
| | Actual Positive ($y_i=1$) | Actual Negative ($y_i=0$)| |--- |:-: |:-: | | Pred. Positive ($c_i=1$) | $C_{TP_i}=C_a$ | $C_{FP_i}=C_a$ | | Pred. Negative ($c_i=0$) | $C_{FN_i}=Amt_i$ | $C_{TN_i}=0$ |
Where:
- $C_{FN_i}$ = Amount of the transaction $i$
- $C_a$ is the administrative cost of dealing with an alert
For more info see [Correa Bahnsen et al., 2014]
# The cost matrix is already calculated for the dataset
# cost_mat[C_FP,C_FN,C_TP,C_TN]
print(data.cost_mat[[10, 17, 50]])
[[ 10. 18.89 10. 0. ] [ 10. 1563.82 10. 0. ] [ 10. 26.06 10. 0. ]]
Financial savings¶
The financial cost of using a classifier $f$ on $\mathcal{S}$ is calculated by
$$ Cost(f(\mathcal{S})) = \sum_{i=1}^N y_i(1-c_i)C_{FN_i} + (1-y_i)c_i C_{FP_i}.$$
Then the financial savings are defined as the cost of the algorithm versus the cost of using no algorithm at all.
$$ Savings(f(\mathcal{S})) = \frac{ Cost_l(\mathcal{S}) - Cost(f(\mathcal{S}))} {Cost_l(\mathcal{S})},$$
where $Cost_l(\mathcal{S})$ is the cost of the costless class
Models Savings¶
costcla.metrics.savings_score(y_true, y_pred, cost_mat)¶
# Calculation of the cost and savings
from costcla.metrics import savings_score, cost_loss
# Evaluate the savings for each model
results["Savings"] = np.zeros(results.shape[0])
for model in ci_models:
results["Savings"].loc[model] = savings_score(y_test, classifiers[model]["c"], cost_mat_test)
Models Savings¶
fig_sav()
Threshold Optimization¶
Convert a classifier cost-sensitive by selecting a proper threshold from training instances according to the savings
Threshold Optimization - Code¶
costcla.models.ThresholdingOptimization(calibration=True)
fit(y_prob_train=None, cost_mat, y_true_train)
- Parameters
- y_prob_train : Predicted probabilities of the training set
- cost_mat : Cost matrix of the classification problem.
- y_true_cal : True class
predict(y_prob)
Parameters
- y_prob : Predicted probabilities
Returns
- y_pred : Predicted class
Threshold Optimization¶
from costcla.models import ThresholdingOptimization
for model in ci_models:
classifiers[model+"-TO"] = {"f": ThresholdingOptimization()}
# Fit
classifiers[model+"-TO"]["f"].fit(classifiers[model]["p_train"], cost_mat_train, y_train)
# Predict
classifiers[model+"-TO"]["c"] = classifiers[model+"-TO"]["f"].predict(classifiers[model]["p"])
print('New thresholds')
for model in ci_models:
print(model + '-TO - ' + str(classifiers[model+'-TO']['f'].threshold_))
New thresholds DT-TO - 0.0128205128205 RF-TO - 0.0253164556962
Threshold Optimization¶
fig_sav()
Models Savings¶
- There are significant differences in the results when evaluating a model using a traditional cost-insensitive measures
- Train models that take into account the different financial costs
Example-Dependent Cost-Sensitive Classification
*Why "Example-Dependent"¶
Cost-sensitive classification ussualy refers to class-dependent costs, where the cost dependends on the class but is assumed constant accross examples.
In fraud detection, different transactions have different amounts, which implies that the costs are not constant
Bayes Minimum Risk (BMR)¶
The BMR classifier is a decision model based on quantifying tradeoffs between various decisions using probabilities and the costs that accompany such decisions.
In particular:
$$ R(c_i=0|\mathbf{x}_i)=C_{TN_i}(1-\hat p_i)+C_{FN_i} \cdot \hat p_i, $$and $$ R(c_i=1|\mathbf{x}_i)=C_{TP_i} \cdot \hat p_i + C_{FP_i}(1- \hat p_i), $$
BMR Code¶
costcla.models.BayesMinimumRiskClassifier(calibration=True)
fit(y_true_cal=None, y_prob_cal=None)
- Parameters
- y_true_cal : True class
- y_prob_cal : Predicted probabilities
predict(y_prob,cost_mat)
Parameters
- y_prob : Predicted probabilities
- cost_mat : Cost matrix of the classification problem.
Returns
- y_pred : Predicted class
BMR Code¶
from costcla.models import BayesMinimumRiskClassifier
for model in ci_models:
classifiers[model+"-BMR"] = {"f": BayesMinimumRiskClassifier()}
# Fit
classifiers[model+"-BMR"]["f"].fit(y_test, classifiers[model]["p"])
# Calibration must be made in a validation set
# Predict
classifiers[model+"-BMR"]["c"] = classifiers[model+"-BMR"]["f"].predict(classifiers[model]["p"], cost_mat_test)
for model in ci_models:
# Evaluate
results.loc[model+"-BMR"] = 0
results.loc[model+"-BMR", measures.keys()] = \
[measures[measure](y_test, classifiers[model+"-BMR"]["c"]) for measure in measures.keys()]
results["Savings"].loc[model+"-BMR"] = savings_score(y_test, classifiers[model+"-BMR"]["c"], cost_mat_test)
BMR Results¶
fig_sav()
BMR Results¶
Why so important focusing on the Recall
- Average cost of a False Negative
print(data.data[data.target == 1, 2].mean())
2231.760665914221
- Average cost of a False Positive
print(data.cost_mat[:,0].mean())
10.0
BMR Results¶
- Bayes Minimum Risk increases the savings by using a cost-insensitive method and then introducing the costs
- Why not introduce the costs during the estimation of the methods?
Cost-Sensitive Decision Trees (CSDT)¶
A a new cost-based impurity measure taking into account the costs when all the examples in a leaf
costcla.models.CostSensitiveDecisionTreeClassifier(criterion='direct_cost', criterion_weight=False, pruned=True)
Cost-Sensitive Random Forest (CSRF)¶
Ensemble of CSDT
costcla.models.CostSensitiveRandomForestClassifier(n_estimators=10, max_samples=0.5, max_features=0.5,combination='majority_voting)```
CSDT & CSRF Code¶
from costcla.models import CostSensitiveDecisionTreeClassifier
from costcla.models import CostSensitiveRandomForestClassifier
classifiers = {"CSDT": {"f": CostSensitiveDecisionTreeClassifier()},
"CSRF": {"f": CostSensitiveRandomForestClassifier(combination='majority_bmr')}}
# Fit the classifiers using the training dataset
for model in classifiers.keys():
classifiers[model]["f"].fit(X_train, y_train, cost_mat_train)
if model == "CSRF":
classifiers[model]["c"] = classifiers[model]["f"].predict(X_test, cost_mat_test)
else:
classifiers[model]["c"] = classifiers[model]["f"].predict(X_test)
CSDT & CSRF Results¶
fig_sav()
Lessons Learned (so far ...)¶
- Selecting models based on traditional statistics does not give the best results in terms of cost
- Models should be evaluated taking into account real financial costs of the application
- Algorithms should be developed to incorporate those financial costs

CostCla Library¶
CostCla is a Python open source cost-sensitive classification library built on top of Scikit-learn, Pandas and Numpy.
Source code, binaries and documentation are distributed under 3-Clause BSD license in the website http://albahnsen.com/CostSensitiveClassification/
CostCla Algorithms¶
Cost-proportionate over-sampling [Elkan, 2001]
SMOTE [Chawla et al., 2002]
Cost-proportionate rejection-sampling [Zadrozny et al., 2003]
Thresholding optimization [Sheng and Ling, 2006]
Bayes minimum risk [Correa Bahnsen et al., 2014a]
Cost-sensitive logistic regression [Correa Bahnsen et al., 2014b]
Cost-sensitive decision trees [Correa Bahnsen et al., 2015a]
Cost-sensitive ensemble methods: cost-sensitive bagging, cost-sensitive pasting, cost-sensitive random forest and cost-sensitive random patches [Correa Bahnsen et al., 2015c]
CostCla Databases¶
Credit Scoring1 - Kaggle credit competition [Data], cost matrix: [Correa Bahnsen et al., 2014]
Credit Scoring 2 - PAKDD2009 Credit [Data], cost matrix: [Correa Bahnsen et al., 2014a]
Direct Marketing - PAKDD2009 Credit [Data], cost matrix: [Correa Bahnsen et al., 2014b]
Churn Modeling, soon
Fraud Detection, soon
Future Work¶
- CSDT in Cython
- Cost-sensitive class-dependent algorithms
- Sampling algorithms
- Probability calibration (Only ROCCH)
- Other algorithms
- More databases
You find the presentation and the IPython Notebook here:
albahnsen/CostSensitiveClassification/blob/ master/doc/tutorials/slides_edcs_fraud_detection.ipynb#/