#!/usr/bin/env python
# coding: utf-8

# <h1 style="text-align:center">Mass-Spring-Damper System with Direct Force Input</h1>
# <h3 style="text-align:center"> MCHE 485: Mechanical Vibrations</h3> 
# <p style="text-align:center">Dr. Joshua Vaughan <br>
# <a href="mailto:joshua.vaughan@louisiana.edu">joshua.vaughan@louisiana.edu</a><br>
# http://www.ucs.louisiana.edu/~jev9637/   </p>

# <p style="text-align:center">
# 	<img src="http://shared.crawlab.org/MassSpringDamper_DirectForce_Horiz.png" alt="A Direct-Force Mass-Spring-Damper System" width=50%/></a><br>
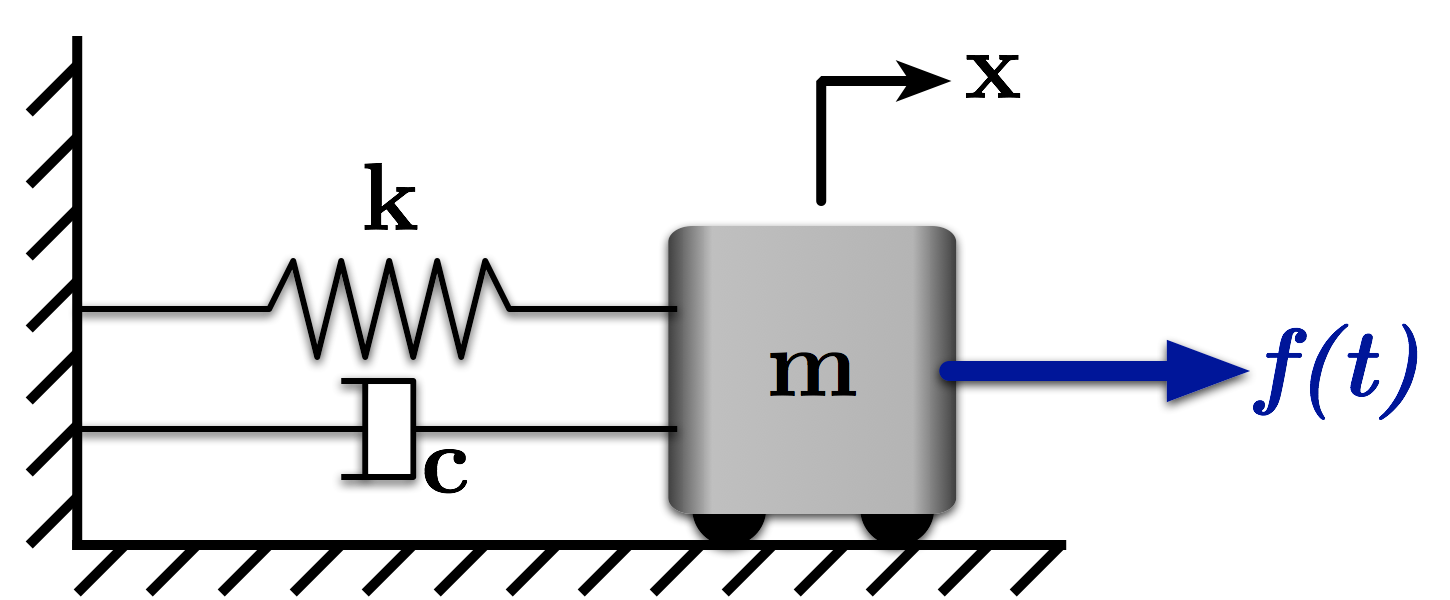
#     <strong> Figure 1: A Direct Force Mass-Spring-Damper System </strong>
# </p>
# 
# This notebook simluates the free vibration of a simple mass-spring-damper system like the one shown in Figure 1. More specifically, we'll look at how system response to non-zero initial conditions. 
# 
# The equation of motion for the system is:
# 
# $ \quad m \ddot{x} + c \dot{x} + kx = f $
# 
# We could also rewrite this equation by dividing by the mass, $m$.
# 
# $ \quad \ddot{x} + \frac{c}{m}\dot{x} + \frac{k}{m}x = \frac{f}{m}$
# 
# or equivalently:
# 
# $ \quad \ddot{x} = - \frac{k}{m}x - \frac{c}{m}\dot{x} + \frac{f}{m}$
# 
# For information on how to obtain this equation, you can see the lectures at the [class website](http://www.ucs.louisiana.edu/~jev9637/MCHE485.html).

# To simluate this system using a numerical solver, we need to rewrite this equation of motion, which is a 2nd-order differential equation, as a system of 1st-order differential equations.
# 
# To do so, define a state vector as $ \bar{w} = \left[x \ \dot{x}\right]^T $. We can also define an input vector as  $\bar{u} = \left[f \right]$. Since we only have one input to this system, the input vector only has one element.
# 
# Then, the system of first-order ODEs we have to solve is:
# 
# $ \quad \dot{\bar{w}} = g(\bar{w}, \bar{u}, t) $
# 
# Writing these out, we have:
# 
# $ \quad \dot{\bar{w}}  = \left[\dot{x} \right.$
# 
# $\phantom{\quad \dot{\bar{w}}  = \left[\right.}\left. -\frac{k}{m}x - \frac{c}{m}\dot{x} - \frac{f}{m}\right] $
# 
# Now, we can use that system of 1st-order differential equations to simulate the system.
# 
# To begin we will import the NumPy library, the matplotlib plotting library, and the ```odeint``` ODE solver from the SciPy library.

# In[1]:


import numpy as np              # Grab all of the NumPy functions with nickname np


# In[2]:


get_ipython().run_line_magic('matplotlib', 'inline')

# Import the plotting functions 
import matplotlib.pyplot as plt


# In[3]:


# Import the ODE solver
from scipy.integrate import odeint


# We need to define two functions for the differential equation solver to use. The first is just the system of differential equations to solve. I've defined it below by ```eq_of_motion()```. It is just the system of equations we wrote above. The second is the input force as a function of time. I have called it ```f()``` below. Here, it is just a pulse input in force, lasting 0.5 second.

# In[4]:


def eq_of_motion(w, t, p):
    """
    Defines the differential equations for the direct-force mass-spring-damper system.

    Arguments:
        w :  vector of the state variables:
        t :  time
        p :  vector of the parameters:
    """
    x, x_dot = w
    m, k, c, StartTime, F_amp = p

    # Create sysODE = (x', x_dot')
    sysODE = [x_dot,
              -k/m * x - c/m * x_dot + f(t, p)/m]
    return sysODE


def f(t, p):
    """
    defines the disturbance force input to the system
    """
    m, k, c, StartTime, F_amp = p
    
    # Select one of the two inputs below
    # Be sure to comment out the one you're not using
    
    # Input Option 1: 
    #    Just a step in force beginning at t=DistStart
    # f = F_amp * (t >= DistStart)
    
    # Input Option 2:
    #    A pulse in force beginning at t=StartTime and ending at t=(StartTime + 0.5)
    f = F_amp * (t >= StartTime) * (t <= StartTime + 0.5)
    
    return f


# In[5]:


# Define the System Parameters
m = 1.0                     # kg
k = (2.0 * np.pi)**2        # N/m (Selected to give an undamped natrual frequency of 1Hz)
wn = np.sqrt(k / m)         # Natural Frequency (rad/s)

z = 0.1                     # Define a desired damping ratio
c = 2 * z * wn * m          # calculate the damping coeff. to create it (N/(m/s))


# In[6]:


# Set up simulation parameters

# ODE solver parameters
abserr = 1.0e-9
relerr = 1.0e-9
max_step = 0.01
stoptime = 10.0
numpoints = 10001

# Create the time samples for the output of the ODE solver
t = np.linspace(0.0, stoptime, numpoints)

# Initial conditions
x_init = 0.0                        # initial position
x_dot_init = 0.0                    # initial velocity

# Set up the parameters for the input function
StartTime = 0.5              # Time the f(t) input will begin
F_amp = 10.0                # Amplitude of Disturbance force (N)

# Pack the parameters and initial conditions into arrays 
p = [m, k, c, StartTime, F_amp]
x0 = [x_init, x_dot_init]


# Now, we will actually call the ode solver, using the ```odeint()``` function from the SciPy library. For more information on ```odeint```, see [the SciPy documentation](http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html).

# In[7]:


# Call the ODE solver.
resp = odeint(eq_of_motion, x0, t, args=(p,), atol=abserr, rtol=relerr,  hmax=max_step)


# The solver returns the time history of each state. To plot an individual response, we just simply pick the corresponding column. Below, we'll plot the position of the mass as a function of time.

# In[8]:


# Make the figure pretty, then plot the results
#   "pretty" parameters selected based on pdf output, not screen output
#   Many of these setting could also be made default by the .matplotlibrc file

# Set the plot size - 3x2 aspect ratio is best
fig = plt.figure(figsize=(6, 4))
ax = plt.gca()
plt.subplots_adjust(bottom=0.17, left=0.17, top=0.96, right=0.96)

# Change the axis units to serif
plt.setp(ax.get_ymajorticklabels(),family='serif',fontsize=18)
plt.setp(ax.get_xmajorticklabels(),family='serif',fontsize=18)

ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')

ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')

# Turn on the plot grid and set appropriate linestyle and color
ax.grid(True,linestyle=':',color='0.75')
ax.set_axisbelow(True)

# Define the X and Y axis labels
plt.xlabel('Time (s)', family='serif', fontsize=22, weight='bold', labelpad=5)
plt.ylabel('Position', family='serif', fontsize=22, weight='bold', labelpad=10)

# Plot the first element of resp for all time. It corresponds to the position.
plt.plot(t, resp[:,0], linewidth=2, linestyle = '-', label=r'Response')

# uncomment below and set limits if needed
# xlim(0,5)
# ylim(0,10)

# # Create the legend, then fix the fontsize
# leg = plt.legend(loc='upper right', fancybox=True)
# ltext  = leg.get_texts()
# plt.setp(ltext,family='serif',fontsize=18)

# Adjust the page layout filling the page using the new tight_layout command
plt.tight_layout(pad = 0.5)

# save the figure as a high-res pdf in the current folder
# It's saved at the original 6x4 size
# plt.savefig('MCHE485_DirectForcePulseWithDamping.pdf')

fig.set_size_inches(9, 6) # Resize the figure for better display in the notebook


# <hr style="border: 0px;        height: 1px;        text-align: center;        background: #333;        background-image: -webkit-linear-gradient(left, #ccc, #333, #ccc);        background-image:    -moz-linear-gradient(left, #ccc, #333, #ccc);        background-image:     -ms-linear-gradient(left, #ccc, #333, #ccc);        background-image:      -o-linear-gradient(left, #ccc, #333, #ccc);">

# #### Licenses
# Code is licensed under a 3-clause BSD-style license. See the licenses/LICENSE.md file.
# 
# Other content is provided under a [Creative Commons Attribution-NonCommercial 4.0 International License](http://creativecommons.org/licenses/by-nc/4.0/), CC-BY-NC 4.0.

# In[9]:


# This cell will just improve the styling of the notebook
from IPython.core.display import HTML
import urllib.request
response = urllib.request.urlopen("https://cl.ly/1B1y452Z1d35")
HTML(response.read().decode("utf-8"))